基于H-ABC算法的并行测试任务优化研究

和 枫，王晓明，叶志鹏，沈海阔

（1.北京宇航系统工程研究所，北京，100076；2.北京交通大学，北京，100044）

0 引言

测试在制造业，尤其是在航空航天以及特种设备制造领域中具有举足轻重的作用，新的产品开发通常需要一系列的测试项目。一般来说，每台设备由多个子系统组成，每个子系统都需要通过一些特定的测试项目。要测试的子系统被命名为待测单元，待测单元的特定测试项被命名为测试任务。待测单元的不同测试任务可能有预定的技术测试顺序，并且取决于不同类型的资源（仪器）。技术测试顺序的限制来源于测试任务的工程需求，即部分测试任务必须在其他相关任务完成后才能开展测试。

对于并行测试任务其目标可以是单一的，也可以是多个。Jain和Grossman［1］首先将并行测试任务调度建模为一个混合整数线性规划模型，该模型将两个相关目标加权为单个优化目标。与上述线性加权法不同，Lu等［2-6］针对该优化问题提出了一系列基于帕累托法则的优化方法，主要是采用NSGA-II作为算法框架［3-5］，提出可变邻域方法使交叉跨度合理［5］，利用混沌映射避免陷入局部最优［4］，其中考虑了最小化最大测试完成时间和平均工作量两个待优化目标。此外，其对特定场景下的单目标优化也进行了充分的研究。Do Ngoc等［7］考虑大型发动机测试过程的额外空间和时间约束，利用遗传算法来寻找候选项目的最佳组合，以获得最大利润。对于具有单一目标的标准TTSP，Lu 和Zhang［8］采用分布估计算法求解测试任务排序，并结合禁忌搜索防止迂回搜索。Shi 等［9］提出了解决TTSP 中资源冲突的方案选择规则，并开发了遗传算法来寻找合适的任务序列。随后，Yang等［10］在充分考虑预先确定的技术测试顺序的基础上，重点研究了标准TTSP，提出了隐含序列寻找过程和基于序列的迭代优化过程，以减少计算时间。Liao等［11］研究了在有交货期限制的过载情况下的加权任务，其目标是使延迟任务的总权重值最小。约束满足问题通常出现在拓扑学研究领域［12］，其主要特点是变量之间存在指定的拓扑关系［13］，但约束满足技术也已广泛应用于规划和调度等领域［14］。求解约束满足问题的关键步骤是构造一个不违反任何拓扑关系约束的可行调度［15］。

并行测试任务调度在于缩短测试进程的最终完成时间，对于本文而言，每个测试任务的可用资源都有各自的依赖关系。因此，需要设计有效的算法保证各测试任务在依赖资源无冲突的前提下，满足测试任务间的既定时序依赖关系，而国内外学者对此类问题鲜有研究。本研究通过对每个任务编码以及输入既定各测试任务间的时序约束与任务与资源间的依赖关系，通过设计有效的人工蜂群启发式算法（Hybrid artifical Bee Colong，H-ABC）进行优化，以获得各测试任务在其相应资源上的先后安排，同时使得最终测试项目的完成时间最小化。

1 H-ABC算法理论研究

首先通过定义以下符号集对本项目所需解决的问题做如下简要概述。令集合T={ti：1 ≤i≤m}表示m个测试任务，集合R={rk：1 ≤k≤n}表示n个测试所需的资源或设备，集合τ={τi：1 ≤i≤m}对应于所有测试任务的时间消耗，TR是一个m×n维的矩阵，表示测试任务和资源之间的依赖关系。矩阵TS表示预定的技术测试顺序矩阵，与实际问题需要满足的约束有关，例如TS(1)=[i，j]表示对任务ti的测试必须在对任务tj的前面。为了实现并行测试，可以通过预定的线程数量d来同时处理不同的测试任务，所有满足TS限制的时间序列都可以被认为是可行的解决方案。

另外，本项目所需解决的问题可以做如下改进：

a）任何资源最多可以同时由一个测试任务占用；

b）占用资源的时间消耗等于相关测试任务的时间消耗；

c）所有测试任务的排序必须满足预定的技术测试顺序；

d）所有资源上同时测试的任务数量必须小于预定的线程数量。这个问题的目标是尽量减少上次测试任务的完成时间。

为建立一个标准的整数规划模型，以下内容首先定义了相关的决策变量。令二值变量zij∈{0，1}表示任务ti与任务tj之间的排布关系，其中zij=1表示任务tj排布在任务ti之后（可以不连续），反之表示任务tj排布在任务ti之前。令非负整型变量si表示任务ti的最早开始测试时间，因此任务ti完成测试的时间为si+τi。非负整型变量Tmax表示整个并行测试系统的完工时间。此外，M表示为一个极大的正整数，在数学模型中对非关键约束起到虚化的作用。

该问题的混合整数规划线性模型建立如下：

式（1）表示为模型的目标函数，即为最小化整个系统的总测试时间。剩余公式定义了本模型的约束和决策变量。约束（2）为各测试任务完工时间的时序约束。当TS(i，j)=1 时，约束1 转化为si+τi≤sj+τj，即要求任务tj的结束时间大于任务ti；反之，模型中没有任务tj与任务ti的结束约束。约束（3）、（4）是保证多任务占用资源的非冲突约束。在约束（3）和约束（4）中，当存在条件TR(i，k)·TS(j，k)=1 时，表明任务ti与任务tj都与资源rk有关联。为避免出现这两个任务抢占同一资源的情况，任务ti与任务tj必然存在其完成时间与开始时间的时序关系。因此，约束（3）与约束（4）有效，反之，约束（3）与约束（4）不存在于模型中。同时，二值变量zij保证了两个任务之间无冲突的时序关系；当zij=1时，约束（3）转换为sj≥τi+si，即任务tj在任务ti之后，而约束（4）无效；当zij=0 时，约束（4）转换为si≥τj+sj，即任务ti在任务tj之后，而约束（3）无效。约束（5）建立了整个系统测试完工时间与测试任务之间的关系，即测试结束时间Tmax为所有测试任务结束时间的最大值。约束（6）和（8）为相应的决策变量定义。

2 H-ABC算法设计

H-ABC 算法首先通过时序递归搜索找到一系列任务隐含序列，然后依次执行全局个体优化、部分个体强化和少量个体淘汰3个主搜索流程，纠正找到的隐含序列ABC 算法的单个编码。在执行全局个体优化和少量个体强化流程时，均会依次执行二进制选择、邻域搜索模块、隐集编码修正，如果随机搜索的概率满足局部搜索条件，还会执行局部搜索模块以及再一次的隐集编码修正。

不同的是，在全局个体优化搜索流程中，每次进入邻域搜索模块的是一个顺序选择个体和一个经过二进制选择的个体；而进入部分个体强化搜索流程中邻域搜索模块两个个体均为经过二进制选择的个体。当执行完全局个体优化和部分个体强化搜索流程后，则会在少量个体淘汰搜索流程阶段对超过限定迭代次数而未优化的个体进行淘汰。最后，经过一次迭代之后更新全局最优个体记录。H-ABC 算法的基本流程如图1所示。

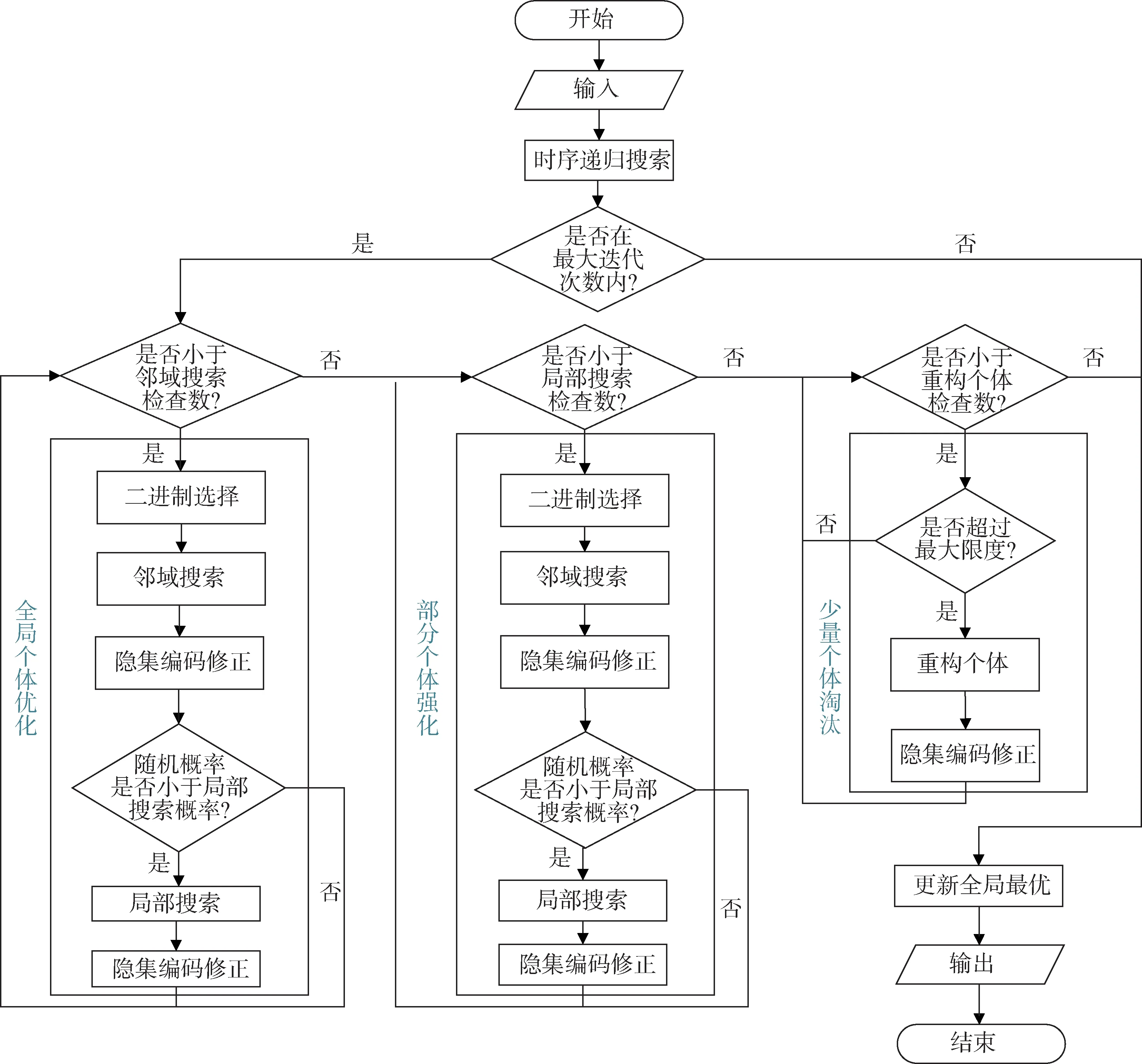
图1 优化算法基本流程Fig.1 Flow chart of the optimization algorithm

图1中的二进制选择主要用来进行高质量个体的选择，其操作为从种群中连续随机选择两个不同的个体，然后选择这对个体中最佳的（适应度值最高的）作为二进制选择的输出个体。

2.1 时序递归搜索技术

时序递归搜索技术是为了找到一系列任务隐含序列，这些序列不违反属于每个待测单元任务的预定测试顺序，然后使用找到的隐含序列纠正ABC 算法的单个编码。让序列表示包含受限制任务w的待测单元的序列，Zw是包含输出子序列⊂Zw的矩阵。此外，Qw=是一个标准序列。标签设置（Lebel Settings，LS）算法是一个典型的递归过程，li=(i，，)表示LS 中的标签，其中i是任务编码，是在任务i结束的分区计划，是任务集，可在节点i扩展。假设lj=(j，，)是li的后继标签，因此可以根据扩展方程对li进行扩展，如式（9）所示。

2.2 邻域搜索技术

邻域搜索技术结合了多点插入算子与多点交换算子，该技术旨在对一个个体编码及其邻域编码实现高质量的子代编码搜索。假设Xt是一个按照顺序选择的个体，Xf为通过二进制选择的一个个体，即为Xt的邻域个体。邻域搜索流程主要依据概率Pnbr执行，如果随机概率大于Pnbr，则只对Xt执行多点交换算子。如果随机概率小于Pnbr，则首先判断两个体的适应度值，如果适应度值相同，仍然只对Xt执行多点交换算子，否则，对两个体执行多点交换算子获得子代编码。

多点插入算子：基于既定的交换点数量与两个个体，通过给定的规则生成子个体。Nnbr表示为既定交换的个体中的节点数量。例如，Xt和Xf可以分别被表示 为Xt=(1，5，3，2，9，8，10，7，4，6) 和Xf=（2，6，5，9，3，1，7，8，4，10）。在Xt中随机选择Nnbr（通常Nnbr=3）个保留点位，则包含保留点位的Xt可以被表示为

其中，x表示Xt的空白位置。随后，从Xf中抽取非Xt中保留点位的其他数值并依次填充入Xt。最终的Xt可以被重新生成为Xt=（6，5，3，2，9，1，7，8，4，10）。上述过程是多点插入算子的标准流程，多点插入算子擅长于在调度问题中更大几率发现质量更高的解。

多点交换算子：针对既定的一个编码，通过多个点的位置交换，从而产生一个新个体编码。多点交换算子依据一个随机产生的交换点数量Ns，然后随机交换Ns个节点的位置，从而产生新编码。该算子旨在通过多点交换方式从而避免算法陷入局部最优的情况。

2.3 局部搜索技术

局部搜索技术结合了贪婪搜索过程，通过局部枚举的方式尽可能地实现高质量解编码的生成。局部搜索算子通过一个弱枚举的循环，最大限度地提升个体解的质量。对于个体编码Xt=（x1，x2，…，xi，…，xm），将第1 个任务编号x1与相邻位置进行交换；如果x1交换后无法提高Xt的质量（适应度值），则重复上述过程；如果x1交换后提高了解Xt的质量（适应度值），则终止循环返回当前生成的新个体。局部搜索算子的执行效率较低，但可以配合弥补其他算子收敛性不强的不足。

本文综合多种搜索技术，可以有效解决多模态问题即存在多个局部最优解的问题，可以更好地探索全局搜索空间，减少陷入局部最优解的风险。同时，可以更好地处理问题的多样性，将问题分解为更小的可管理部分，并针对每个部分选择合适的搜索策略。而传统的启发式算法多采用单一搜索技术求解最优序列，求解效率低，易陷入局部最优，面对复杂问题甚至可能无法求出最优解。

3 实例分析

本部分首先采用随机生成的算例测试H-ABC 的效率和最优性。其中，对于小规模问题采用整数规划精确算法（Mixed Integer Pragramnrg，MIP）作为HABC的对比算法，验证H-ABC的最优性和求解效率。此外，采用了随机生成的大规模算例n=100，以验证H-ABC 算法的极限性能。测试用例提供了小规模算例的具体数据，并通过甘特图展示了大小规模算例的求解结果。

其次，在并行测试任务的真实案例上对算法的性能和优化过程进行了进一步的验证，对优化结果和迭代过程进行了展示。

3.1 小规模用例算法性能测试

小规模测试用例1 如表1 所示，规模为任务数量m=8，资源数量n=7的测试用例数据。

表1 小规模测试用例1Tab.1 Small-scale test example 1

表1 展示了规模为任务数量为m=8 以及资源数量为n=7的一个小规模算例，其中该算例没有任务间的时序约束。表1的算例分别调用了基于MIP模型的商业求解器以及H-ABC 算法求解。两算法都求解到了该算例的最优解，即最优完工时间为Tmax=47，两算法都在1 秒内求解到最优解，其最优解的甘特图如图2所示。

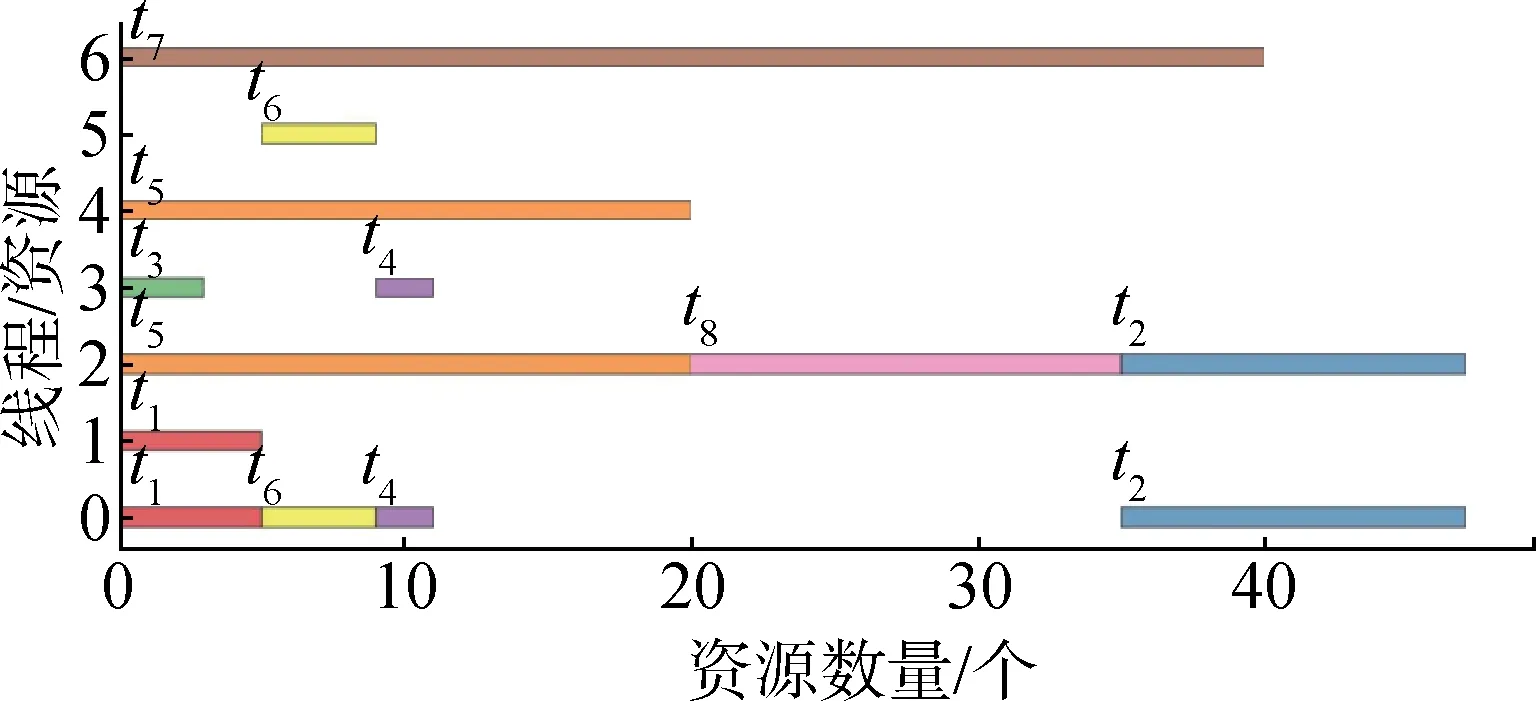
图2 小规模测试用例1结果甘特图Fig.2 Gantt chart of example 1

小规模测试用例2 如表2 所示，规模为任务数量为15，资源数量为5的测试用例数据。

表2 小规模测试用例2Tab.2 Small-scale test example 2

表2展示了任务数量为15以及资源数量为5的一个小规模算例，其中该算例有预定时序约束。表2的算例同样分别调用了MIP模型以及H-ABC算法求解。两算法都求解到了该算例的最优解，即最优完工时间为Tmax=412。两种算法都在7 s内求解到最优解，其最优解的甘特图如图3所示。

图3 小规模测试用例2结果甘特图（有时序约束）Fig.3 Gantt diagchart ram of example 2（with temporal constraints）

图4 展示了表2 数据下没有预定时序约束的算例结果。两算法都求解到了该算例的最优解，即最优完工时间为Tmax=412，MIP 的求解时间为122.6 s，H-ABC的求解时间小于10 s。MIP模型在无时序约束的问题下，求解性能会显著下降。相比于MIP 模型，H-ABC在求解大规模算例方面有着较大优势。

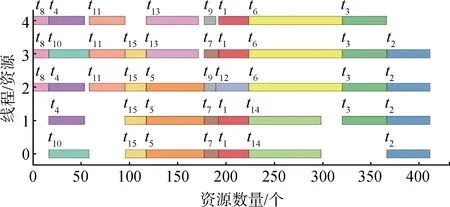
图4 小规模测试用例2结果甘特图（无时序约束）Fig.4 Gantt chart of example 2（without temporal constraints）

3.2 大规模用例算法性能测试

大规模算例：任务数量m=100，资源数量n=10，结果如图5所示。

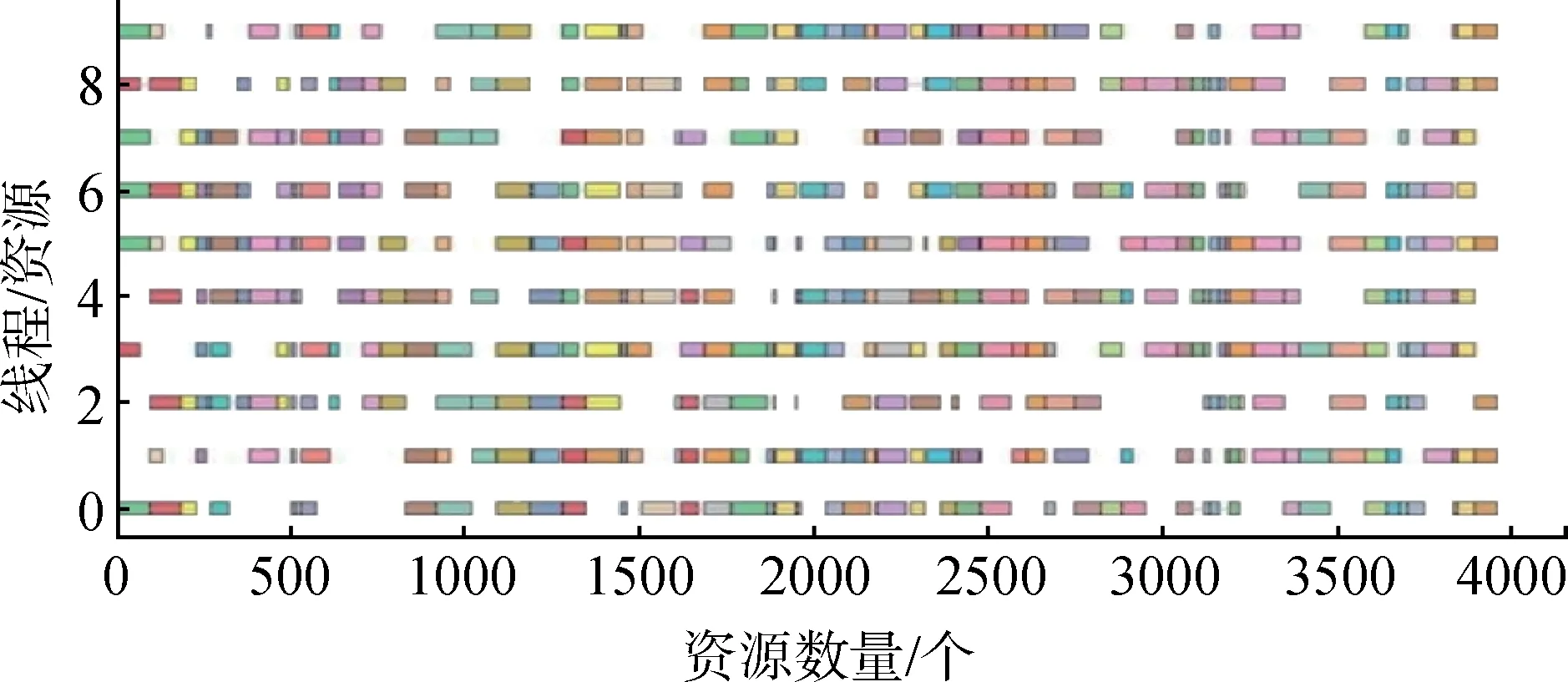
图5 大规模测试用例结果甘特图Fig.5 Gantt chart of large-scale test example

对大规模算例，H-ABC 算法可以完全满性能需求。H-ABC 搜索到最小的完工时间为Tmax=3 964，HABC 的求解时间约为412 s。对于该规模的问题，MIP模型以及常用求解已无法处理。相比现行传统求解器对该问题的求解性能，H-ABC 在求解加大规模算例方面有极大优势。

3.3 算法优化流程展示

图6 至图9 展示了任务数为15，资源数为5 时的规模示例调用H-ABC算法进行迭代收敛的相关结果。其中，邻域搜索概率为0.7，局部搜索概率为0.3，最大迭代次数为100。完工时间随迭代次数的收敛曲线如图6所示。图7至图9则分别展示了第1次、第4次及第5次迭代结果的甘特图，相应的完工时间分别为438 s、415 s、412 s。

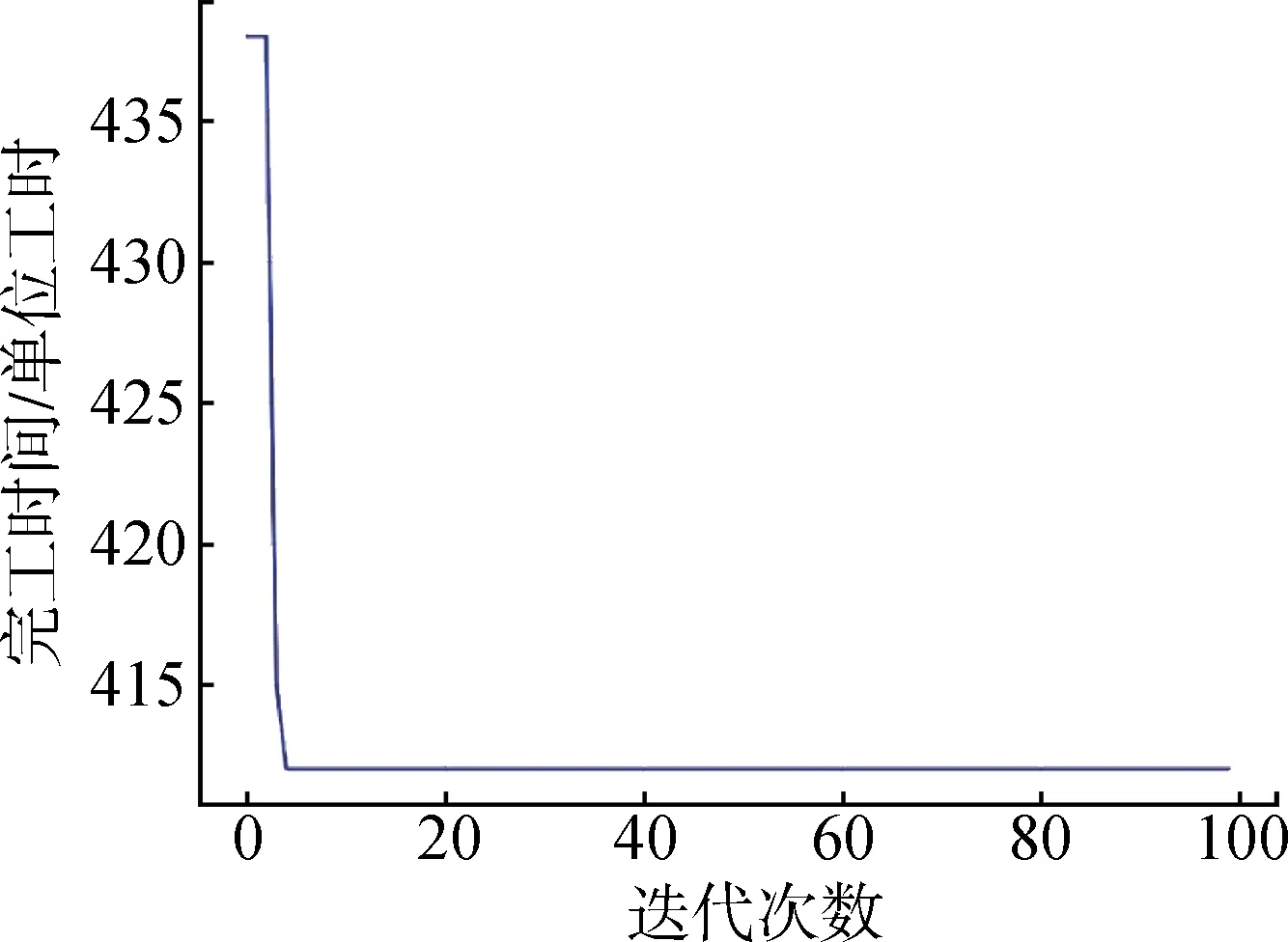
图6 H-ABC求解上述15×5规模示例的算法收敛Fig.6 Algorithm convergence process of the 15×5 scale example

图7 第1次迭代结果的甘特图：完工时间438 sFig.7 Gantt chart of the first iteration: completion time 438 s

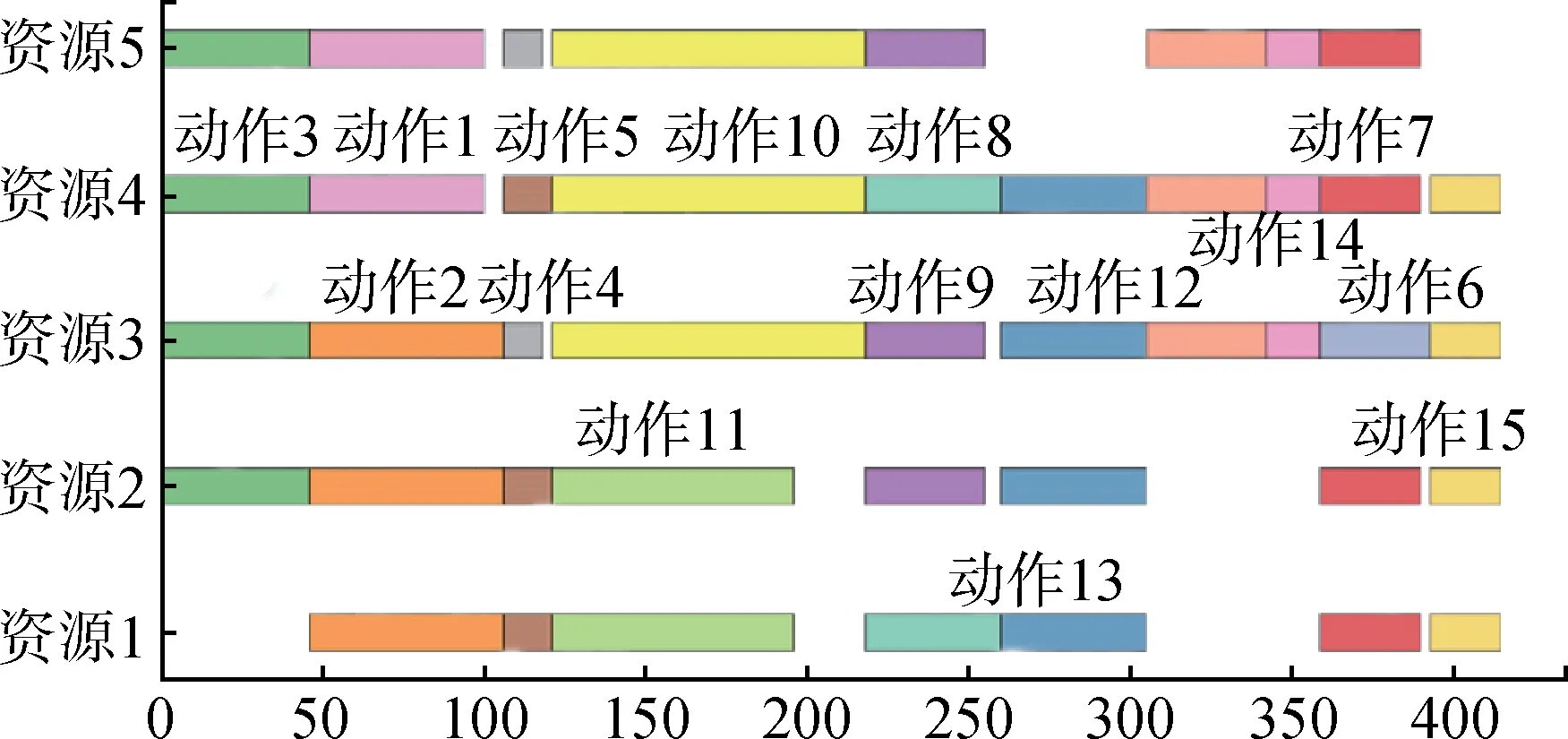
图8 第4次迭代结果的甘特图：完工时间415Fig.8 Gantt chart of the fourth iteration: completion time 415

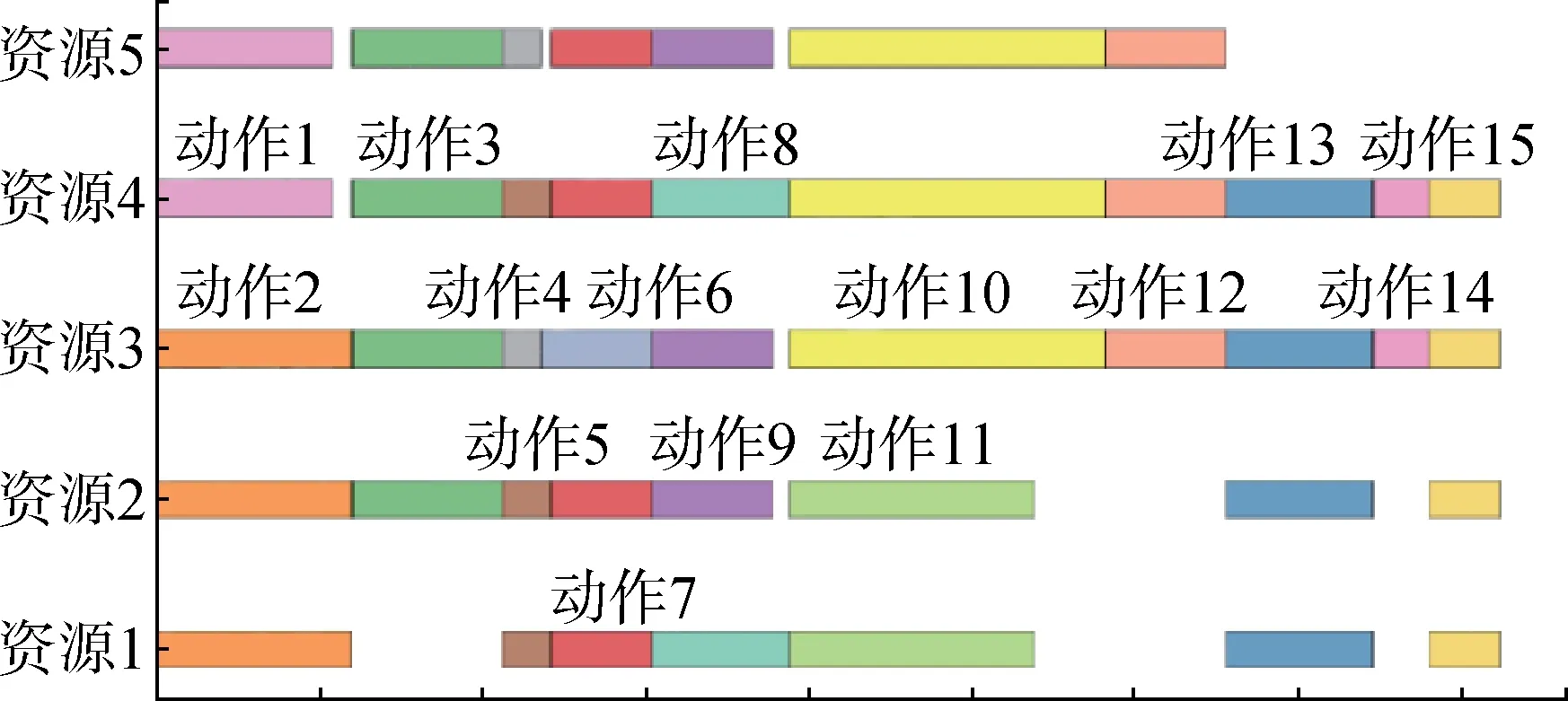
图9 第5次迭代结果的甘特图：完工时间412 sFig.9 Gantt chart of the 5th iteration: completion time 412 s

图10和图11分别展示了任务数为46和80的大规模测试的结果，由于测试任务的规模较大，难以用甘特图去展示其迭代结果，因此只绘制了完工时间和CPU迭代耗时的收敛曲线。由图10a可以看出，完工时间在迭代40次左右趋于稳定，耗时1 064 s；图10b显示了任务数为46 时，进行100 次迭代CPU 耗时229.23 s。当测试任务达到80 次时，完工时间收敛于2 493 s，算法迭代CPU 耗时1 113.62 s，具体结果如图11a和11b所示。

图10 H-ABC求解46×10规模示例性能展示Fig.10 Performance of H-ABC solving 46×10 scale example

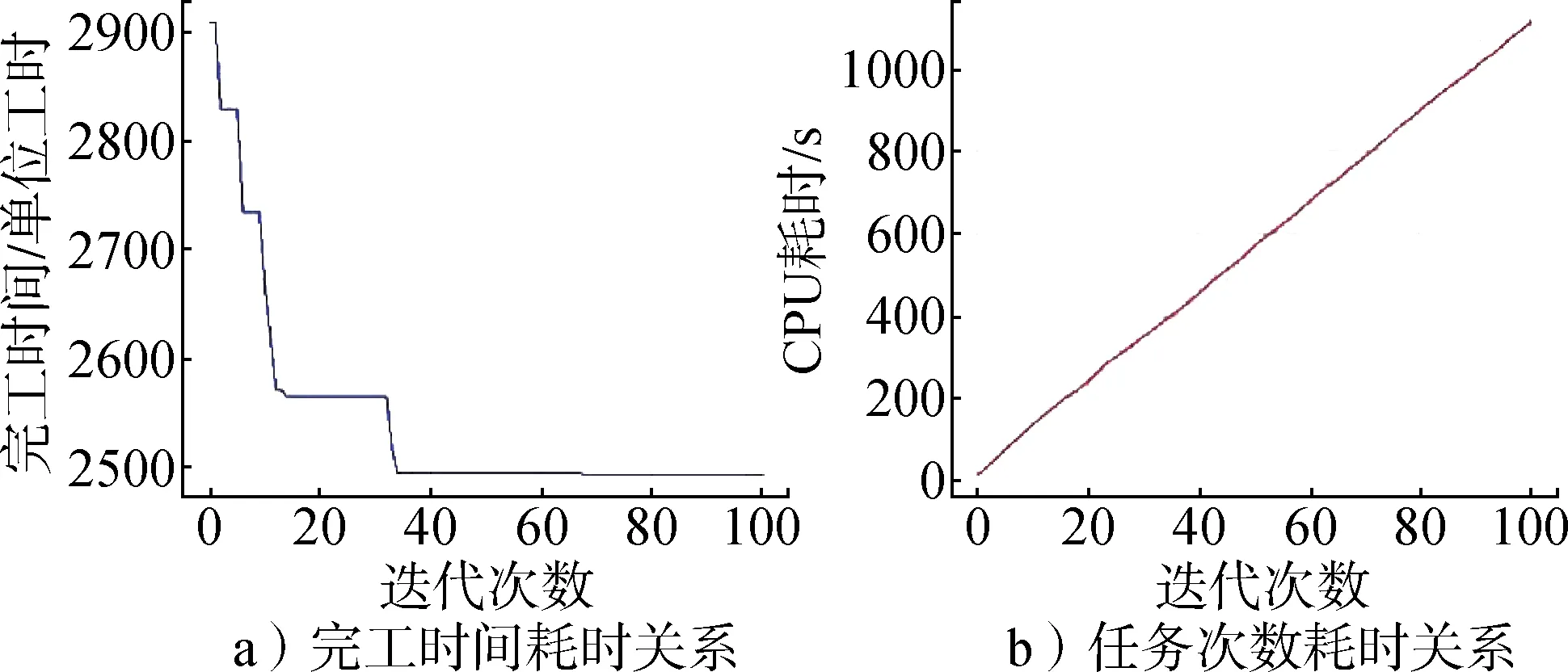
图11 H-ABC求解80×10规模示例性能展示Fig.11 Performance of H-ABC solving 80×10 scale example

4 结束语

H-ABC 算法可以通过迭代的方式找到测试任务的最优方案，极大缩短测试流程所用的总时间。通过小规模用例和大规模用例测试，H-ABC 算法都可以实现目标，验证了算法的普适性。本算法可应用于相关弱约束条件复杂内容执行过程的优化处理，较传统MIP算法表现出更高的收敛效率和执行效果。