一境二构三问：促进概念教学的深度理解——以“倍的认识”教学为例

浙江杭州市钱塘区听涛小学（310018） 龚 玲

杭州师范大学经亨颐教育学院（310018） 徐良盛

【教学背景】

“倍的认识”是人教版教材三年级上册第五单元的内容，该内容是在学生已经初步了解了乘法和除法意义的基础上进行教学的。“倍”是一个重要但相对抽象的概念，与“分数”“百分数”和“比”等概念密切相关，为学生的后续学习提供了基础。

通过前测发现，班级里大约5%的学生能够描述倍数关系，但对于倍的确切含义的理解还较为模糊。例如，对于苹果6 个、梨3 个这样的情境，学生能理解苹果的数量是梨的2 倍，但当苹果和梨的具体数量改变后，有些学生可能感到困惑。这反映部分学生对于“倍”的理解仍然比较表面，还未深入掌握。

基于此，笔者在设计“倍”这一教学内容的教学环节时，有意突出了以下两点。第一，以“2 倍”为切入点，紧紧围绕这个基本的倍数关系开展教学。通过构建直观的“倍”模型，帮助学生充分理解“倍”的本质。第二，通过“变中求不变”的方法，逐步引导学生更深入地理解“倍”的含义。教师鼓励学生从在具体情境中对比逐渐过渡到形式上的对比，同时引导学生通过分析多种具体事物的共性，抽象出事物的数量特征。

【课堂实录】

一、创设情境，初步认识“倍”

师（出示图1）：秋天来了，果园丰收了，小动物们忙着摘水果。请仔细观察，看看能从图中获得哪些数学信息？

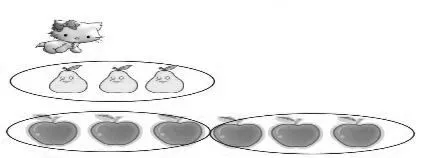
图1

师：苹果和梨的个数有怎样的数量关系？

生1：苹果比梨多3个。

生2：梨比苹果少3个。

生3：苹果的个数是梨的2倍。

师：你是怎么知道苹果的个数是梨的2倍的？

生3：苹果有6个，梨有3个，6里面有2个3。

生4：3+3=6。这也能看出6里面有2个3。

师：是的，两个数量之间，除了“多”和“少”的关系，还有着“倍”的关系。如果我们把3 个梨看作一份（边说边在黑板上圈），苹果有这样的几份呢？对，有这样的2份。我们就说，苹果的个数是梨的2倍。今天我们就要来研究有关“倍”的知识。

【设计解读：学生喜闻乐见又充满童趣的“小动物摘水果”的教学情境，能抓住小学低段学生的心理特点，激发学生的好奇心和求知欲。数一数、算一算这些都是学生常用的方法，为后续新知的教学做好了铺垫。】

二、探究新知，对比中认识“2倍”

1.在变中求不变

师：看！小狗也来摘果了，小狗摘的水果个数有没有倍数关系呢？（出示图2）你是怎么想的？

图2

生1：苹果有4个，草莓有2个，4里面有2个2。

师：谁听懂了？

生2：如果把2 个草莓看作1 份，苹果有这样的2份，因此，苹果的个数是草莓的2倍。

师：是的，如果把2 个草莓看作1 份，苹果有这样的2份，我们就说苹果的个数是草莓的2倍。

师（出示图3）：小象也来了，它摘的水果个数又有着怎样的倍数关系呢？（学生回答略）

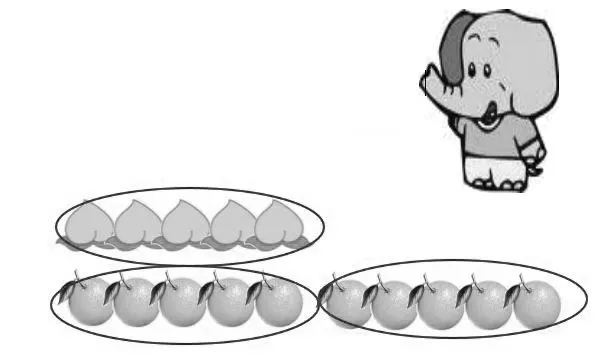
图3

师：我们看看三个小动物摘的水果，它们摘的个数一样吗？（不一样）为什么各自摘的两种水果数量都有2倍关系？

师（将图4-1的信息隐去，得到图4-2）：如果把上面的水果看作1 份，下面的水果有这样的几份？（学生回答略）

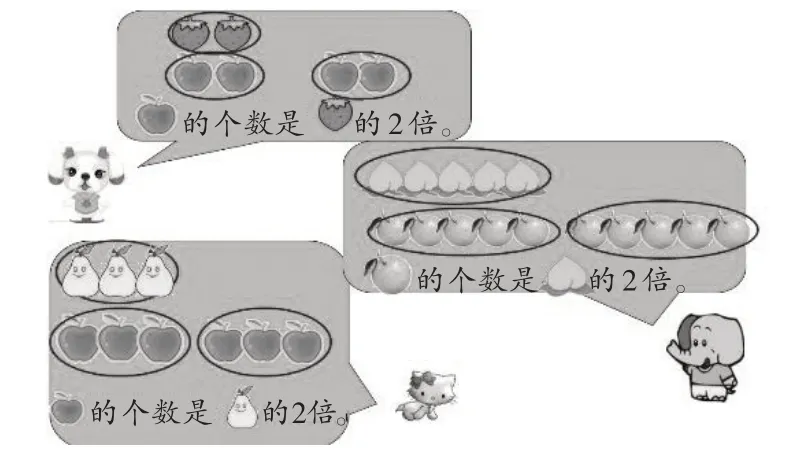
图4-1

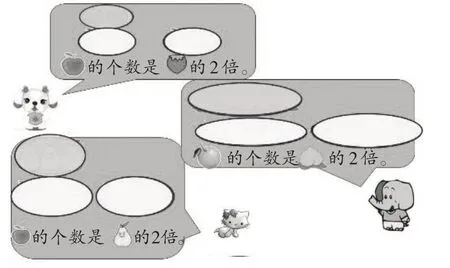
图4-2

师：如果把上面的水果看作1 份，下面的水果都有这样的2 份，因此下面的水果个数都是上面的2 倍。同学们真会观察，能从不同中找到相同点，真棒！

【设计解读：该环节采用图像表征、操作表征、启发谈话、深度思考、合作交流等形式，引导学生将思考过程用“把（ ）看作1 份，（ ）有这样的2份，我们就说（ ）是（ ）的2 倍”这样准确、精练的语言表达出来。一系列学生喜爱的“小动物摘水果”的教学情境充分建构“倍”的直观模型，学生通过观察思考“在变中求不变”，进一步认识“倍”，教师通过追问“水果个数不一样，为什么都有‘2 倍’关系？”引导学生深入理解“倍”的本质。】

2.无序中渗透有序思想

师（出示图5）：小猪摘的水果看上去有点乱。你能从这么乱的图中看出倍数关系吗？你用的是什么办法？

图5

生3：圈一圈，将4 个西瓜看作1 份，菠萝有这样的2份。（教师出示图6）

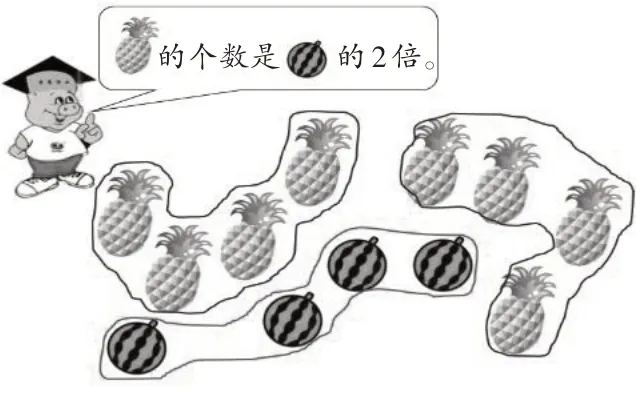
图6

生4：理一理，一一对应重新摆。（教师出示图7）

图7

生5：也可以列式得“8÷4=2”。

师：你们不仅看到了图，还从中看到了数；不光看到了数，还看到了数量之间的关系。真棒！

【设计解读：本环节继续利用“小动物摘水果”的教学情境，由易到难、从有序到无序，层层递进。开放的问题情境，激起了学生思维的火花，满足了不同学生的需求，让不同层次的学生得到不同的发展。】

三、练习中过渡到“多倍”，完善“倍”的认识

师：刚才我们说了那么多2 倍，那么有没有3倍、4 倍甚至更多倍呢？请大家看练习题，找找看两个数量之间的关系。（出示图8）

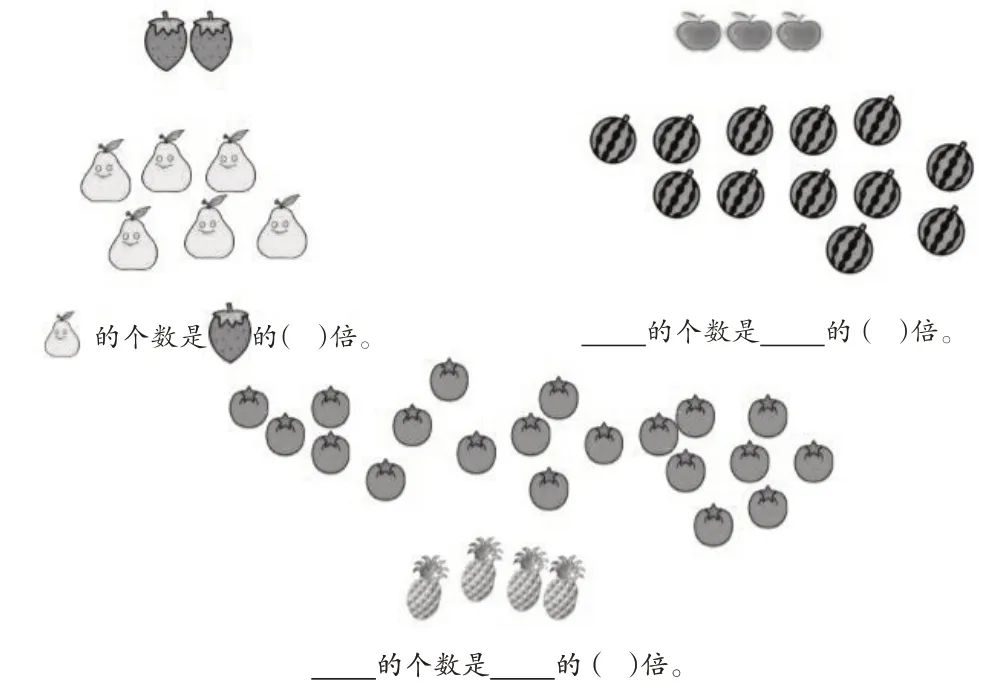
图8

【设计解读：在学生充分认识了2 倍，基本建构了“倍”的模型后，教师通过类比迁移，引导学生自主认识3倍、4倍等多倍关系。】

四、错例辨析中深入理解“倍”

师（出示图9）：小兔也来凑热闹了。小兔说的对吗？

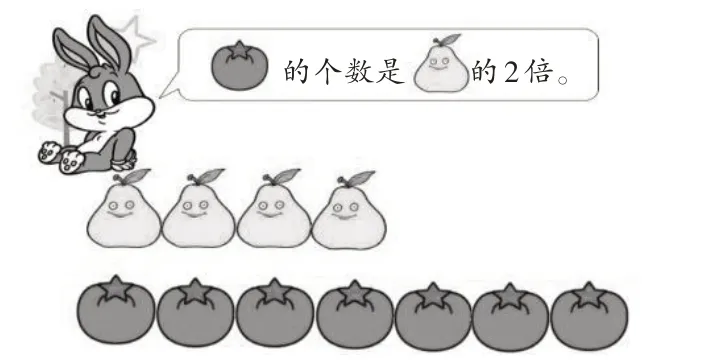
图9

生1：不对，梨有4 个，苹果只有7 个，它们之间不是2倍关系。

师：你分析得很有道理。这里是把什么看作1份？

生2：把4个梨看作1份。

师（出示图10）：这样看，柿子算两份吗，为什么？

图10

生3：不算，因为下面的其中一份只有3 个柿子，必须4个4个地圈，4个为一份，不能随便圈。

师：把4个梨看作1份，柿子也要4个4个地圈，1 份数必须相同。把4 个梨看作1 份的话，怎么改一改柿子的个数才能让柿子的个数是梨的2倍？

生4：加1个柿子。

生5：还可以分别去掉1个梨和1个柿子。

师：你的想法很有创意。这样的话，原来1 份数就变成了3 个。它们还是2 倍关系，即1 份数在变，总数也随之改变。

【设计解读：在学生面对一系列问题，对于“倍”能正确理解后，设计一道“有问题”的练习引发学生的认知冲突，学生呈现“心求通而未得，口欲言而弗能”的愤悱状态。此时提供给学生自主尝试的机会，使学生在畅所欲言中加深对“倍”的理解，同时收获多种纠错的方法。特别是学生还提出了“可以分别去掉1 个梨和1 个柿子”的打破常规的思路，“倍数关系不变，1 份数在变，总数也随之改变”这一结论的提出也水到渠成。心理学家盖耶曾说过“若不允许学生自主尝试和犯错，就将错过最富有成效的学习时刻”，的确如此！】

五、操作中感受比的标准，认识“1倍”

师（出示图11-1）：果园的柿子可多啦，小狗和小兔又来了。小兔想知道她摘的个数是小狗的几倍。小兔摘了几个？你们发现了什么？哦，小狗摘的个数不知道。那你们猜一猜，小狗有可能摘了几个？有几种可能？每一种情况中，小兔摘的个数是小狗的几倍？先独立探究，然后完成下面练习（如图11-2）。

图11-1

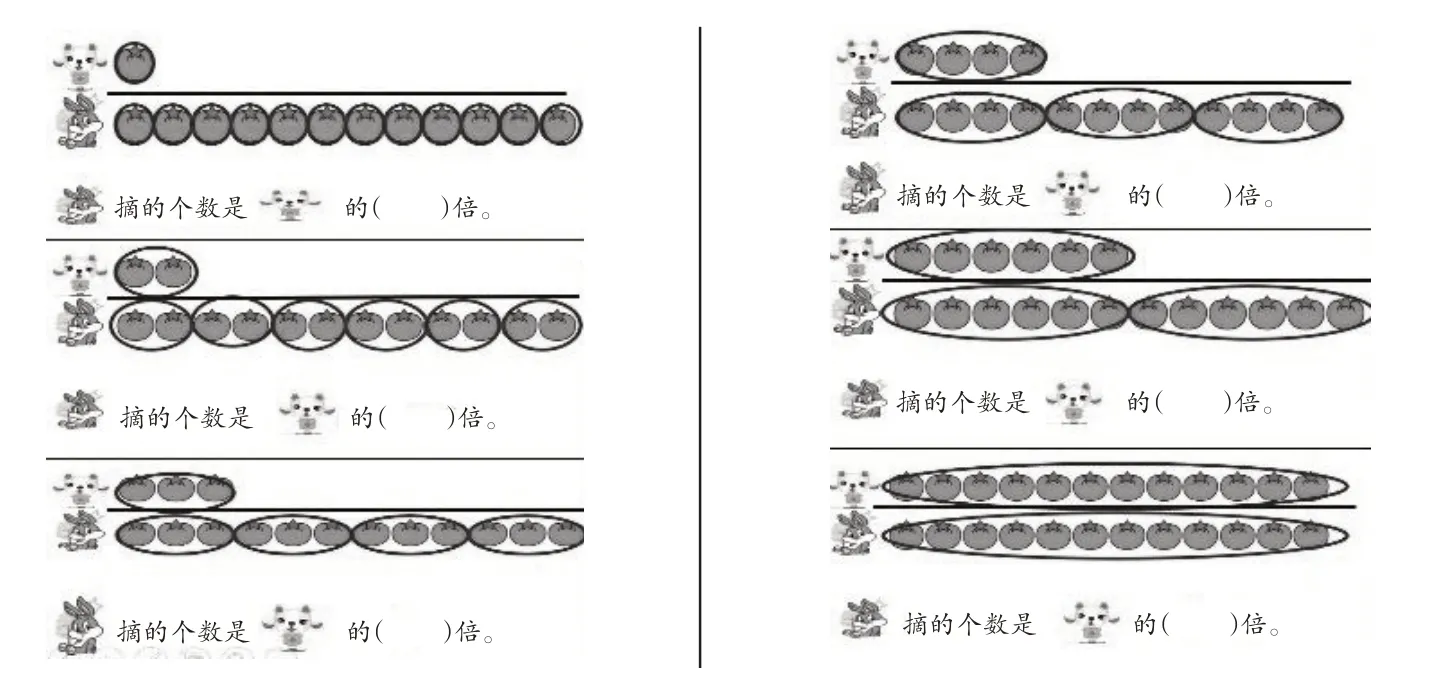
图11-2

师：什么情况下是1倍的关系呢？

生1：当两个数量一样时。

师：为什么小兔摘的个数一直没有变，而这里的倍数关系却在不断地变化呢？

生2：因为小狗摘的个数在变，也就是1份数在变化，所以倍数关系也会随之改变。

【设计解读：这是一道开放题，倍数关系不是独立存在的。小兔摘了12 个，小狗摘的个数不知道，那么小狗摘的个数和12 存在倍数关系的情况就有多种。而题中“摘的个数是的（ ）倍”，实则是求“12 是（ ）的（ ）倍”，也就是大数是小数的几倍。学生很容易得出1、2、3、4、6、12与12的倍数关系，其中难度较大的是1倍和12倍。当小狗摘的个数是12 个，也就是和小兔摘的一样多时，小兔摘的个数是小狗的1倍；当小狗只摘了1个时，小兔摘的个数是小狗的12 倍。此题的教学意义不仅是让学生理解“1 倍”，随着问题“为什么小兔摘的个数一直没有变，而这里的倍数关系却在不断地变化呢？”的提出，学生的思维进入了更深处。】

六、游戏：翻一翻，变中再次感受比的标准

师：小猫咪摘水果累了，想和小朋友们玩个游戏。这里总共有12 个白圆（出示图12-1），老师把其中一个翻了过来，瞧，它变成了黑圆（出示图12-2）。这时白圆有几个？（11 个）黑圆呢？（1 个）。你能用一句话说一说白圆的个数和黑圆的个数之间的倍数关系吗？

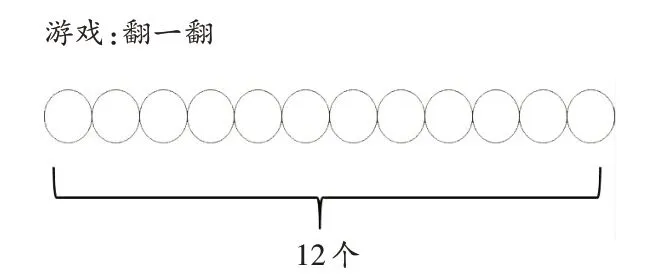
图12-1

图12-2

生1：11白、1黑，白圆的个数是黑圆的11倍。师：再翻一个呢？请说出其中的倍数关系。生2：10白、2黑，白圆的个数是黑圆的5倍。师：如果再翻一个呢？

生3：9白、3黑，白圆是黑圆的3倍。

师：再翻一个呢？

生4：8白、4黑，白圆是黑圆的2倍。

师：猜一猜，接下来还可以怎么翻？谁愿意来翻一下？

……

师：为什么前面我们说“白圆是黑圆的几倍”，现在却变成了“黑圆是白圆的几倍”呢？

生5：因为黑圆个数比白圆的多了。

生6：前面我们是把黑圆看作1份，白圆有这样的几份，就是黑圆的几倍；随着黑圆个数越来越多，我们把少的白圆看作1份，黑圆有这样的几份，我们就说黑圆是白圆的几倍。

师：不难发现，比的标准不一样，倍数关系也会随之变化。

【设计解读：教学接近尾声，高潮没有落幕。游戏环节再次激起学生思维的火花，课堂氛围活跃，学生沉浸在快乐而有深度的学习中。随着白圆不断减少、黑圆不断增加，比较的标准发生了变化，倍数关系也会随之变化。从“倍数关系不变，1份数在变，总数也随之改变”到“1 份数在变，倍数关系随之改变”，再到“比较的标准发生了变化，倍数关系也会随之变化”，真正实现了教学的“三进阶”。】

七、回归生活，全课总结

师：同学们在生活中遇到过倍数关系吗？“把（ ）看作一份，（ ）有这样的（ ）份，我们就说，（ ）是（ ）的（ ）倍。”你能像这样说一说生活中遇到的倍数关系吗？

生1：弟弟有5 支铅笔，我有10 支铅笔，我的铅笔支数是弟弟的2倍。

生2：我有10 本书，同桌有50 本书，同桌的书本数是我的5倍。

生3：我们学校三年级有8 个班，四年级也有8个班，三年级的班级数是四年级的1 倍，也可以说四年级的班级数是三年级的1倍。

师：同学们真是生活的有心人，能举出来这么多关于倍数的例子。的确，有几个1 份数这么多，我们就说它与1份数之间存在几倍的数量关系。

师：今天我们认识了“倍”这个新朋友，你知道了关于“倍”的哪些知识呢？（学生回答略）同学们，祝贺你们成功走进了“倍”的世界，感悟到了数学是源于生活，并应用于生活的。我们将在生活中继续探索更多有关“倍”的知识！

【教学反思】

本节课遵从课程标准要求，精准把握学情，透彻分析教材，将教学内容趣味化、结构化、悬疑式，以培养学生建构“倍”概念这一模型的基本推理意识和推理能力。本课例主要有以下特点。

一、趣味化创设教学情境

正如于漪老师所说，“课的第一锤要敲在学生的心灵上，激发起他们思维的火花”。的确，好的开头可如磁石一般能将学生牢牢吸引。本节课围绕“小动物摘水果”这一教学情境开展“倍”的认识教学，并且这一情境贯穿始终，符合学生身心发展特点，充满童趣又高潮迭起的课堂牢牢吸引了学生的注意力。

二、结构化梳理教学重点

本节课从重点突破“2 倍”入手，引导学生初步理解“倍”的概念，再类比迁移到3倍、4倍及更多倍的学习——这是一条教学的明线；从“倍数关系不变，1 份数在变，总数随之改变”到“总数不变，1 份数在变，倍数关系随之改变”，再到“比较的标准发生变化，倍数关系也会随之变化”，变中有不变——这是一条教学的暗线。皮亚杰指出：“数学是对结构的构建而建立起来的。”明暗叠加的双层次结构化教学设计，将教学步步引向深入。

除此之外，构建“倍”的教学模型过程中，教学板书的结构化为有效突破教学难点提供了有力保障。教师带着学生在圈圈画画中打造了简洁明了、重点突出的板书，有力地引导学生不仅“想得通”，更要“说得清”，将内在思维外化为语言输出，为突破语言表达这一教学目标提供了强有力的“脚手架”。与此同时，在课的最后，教师利用此板书（如图13-1、13-2），将学生的视域从有限的课内数学转移到了广阔的生活数学，实现了从具体到抽象，从课堂到生活的双重教学目标。

图13-1

图13-2

三、悬疑式追问教学难点

教学中，教师的主要任务在于“引”，而学生的主要任务在于“思”。本节课教师在教学难点处的三次追问，将学生的思维步步引向深入。教师的问，问在了教学内容的难点处，问在了学生思维的盲点处。只有教师有的放矢、“拨开迷雾”地追问，才能让学生体会到抽丝剥茧、渐入佳境的“豁然开朗”，学生对“倍”概念的深度理解才能一步步实现！

任何一种教育理念都只有根植于课堂实践这片肥沃的土壤才会具有鲜活的生命力。基于深度理解的教学设计不仅符合认知负荷理论，也是数学智慧课堂的必然选择。这种设计有助于学生深入理解和系统掌握知识，同时感悟到学习内容所体现的思维方法。唯有教师深度理解的教学实践才能促进学生的深度理解真正发生；唯有教师自身在教学上深入思考，才能引领学生的思维进入更深处！