基于膨胀变换的单相自然循环动态比例分析方法研究
李向宾,徐嘉宁,刘宇生,杨 帅,冯明聪,吴 樵
基于膨胀变换的单相自然循环动态比例分析方法研究
李向宾1,2,徐嘉宁1,2,刘宇生3,杨 帅1,2,冯明聪1,2,吴 樵4
(1. 华北电力大学核科学与工程学院,北京 102206;2. 非能动核能安全技术北京市重点实验室,北京 102206; 3. 生态环境部核与辐射安全中心,北京 100082;4. 俄勒冈州立大学,科瓦利斯 97331,美国)
为进一步深入了解动态系统比例分析理论,以单相自然循环系统为研究对象,研究了基于膨胀变换的新型动态比例分析方法,获得了固定长度比例下不同膨胀数所对应的相似数组,并利用RELAP5程序计算了简单矩形环路内对应工况时的自然循环特性,分析了对应关键参数及相似准则数的变化规律。结果发现:在大部分工况下,整个动态过程中模型和原型系统的质量流量误差与冷热段温差误差均在较小范围内;当膨胀数由0.5到1.0增大的过程中,缩比工况的归一化质量流量与归一化温差变化趋势与原型工况逐渐接近,同时流量误差与温差误差均逐渐减小。基于单一膨胀数方法所得的自然循环相似准则数组中,热源数是决定性准则数,而理查森数和斯坦顿数均为非决定性准则数。
膨胀变换;动态比例分析;单相自然循环;比例偏差
比例分析方法为缩比试验台架有效模拟原型系统及实验过程提供了重要理论依据[1],并已被广泛用于核电站相关系统的设计和安全评审[2-7]。但是,之前的研究对于比例偏差的分析多是在稳态特征参数基础上的,即对应的相似准则数以稳态值或初始值作为特征参数,其对于比例偏差的评估也具有静态特征,难以准确评价动态过程。近几年,Reyes提出了一种基于二参数映射的动态比例分析理论(Dynamical System Scaling),在不同的映射条件下,可以推导得到不同的相似准则数[8]。作者首先将此理论应用于水箱重力排放过程的动态比例分析,计算评价了不同缩比工况下水箱内重力排放阶段关键参数的动态变化规律[9],并进一步系统推导了用于单相自然循环系统的同一性DSS方法,对比评价了原双向分层比例方法和同一性DSS方法在比例分析中的不同特点,拓展了DSS方法在自然循环系统动态过程中的应用[10,11]。
为进一步深入评估DSS理论,本文以单相自然循环系统为研究对象,采用与参考文献同一性法不同的映射条件,即利用新的膨胀变换方法,获得了不同膨胀参数下动态比例分析方法所对应的相似数组,并利用RELAP5[12]程序计算其自然循环特性,对比分析了不同工况下缩比模型计算结果和原型计算结果的动态变化规律。
1 基于膨胀变换的比例分析
为便于进行比例分析,对自然循环系统进行简化并建立模型。简化如下:
(1)沿管段轴向的流体流动为一维流动,每个截面上的流体物性参数均保持均匀;
(2)应用Boussinesq近似假设[10,13];
(3)壁面热量损失均忽略不计(热构件除外);
(4)系统管道截面都有相同的截面积(均匀管径)。
基于以上假设,自然循环系统简化成由加热段、上升段、上部水平管段、冷却段、下降段和下部水平段组成的简单矩形环路,如图1所示。
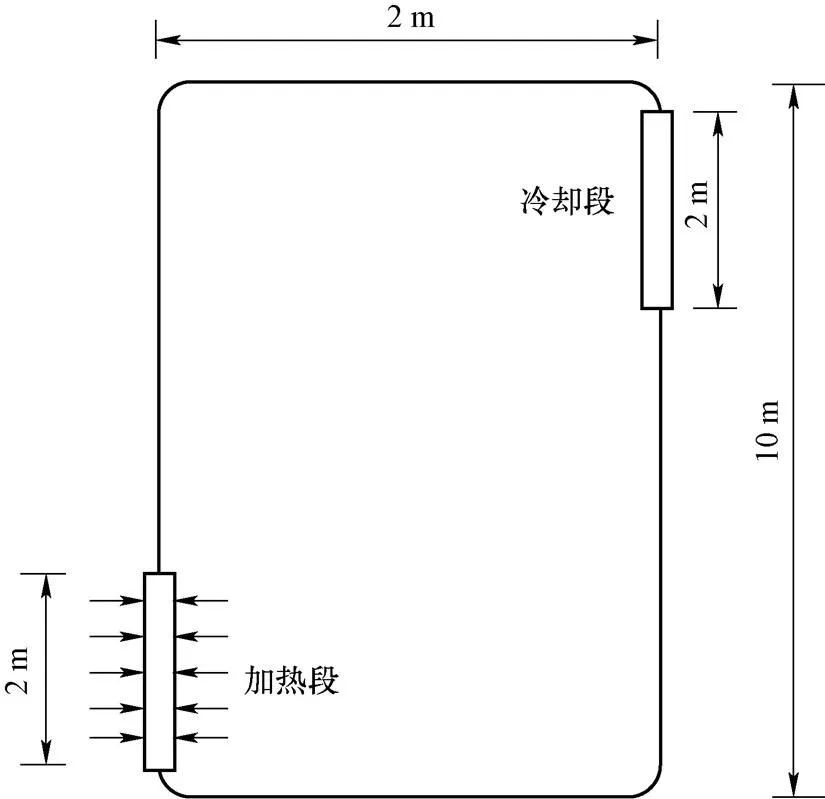
图1 自然循环系统简化模型
基于上述简化模型,可得单相自然循环的动量守恒方程:

将上式变形改写为以下形式:
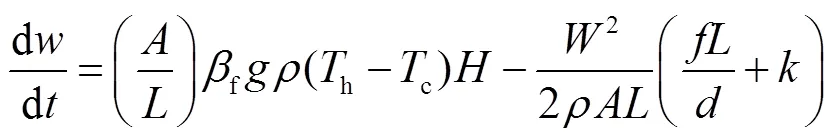

式中:角标与——由回路温差与流动阻力引起的循环流量变化。
对照公式(2),有:

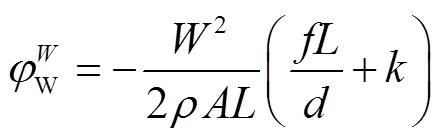

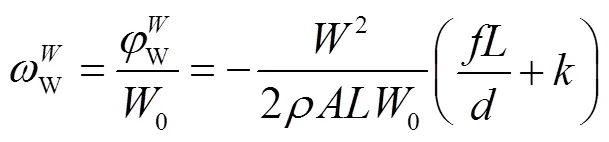
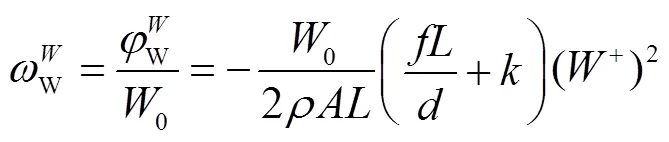
列出自然循环变量的相似准则:

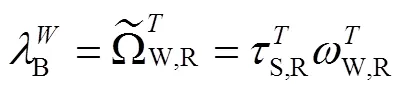

下标M与P——模型与原型的对应参数;
R——模型与原型相关参数的比值。
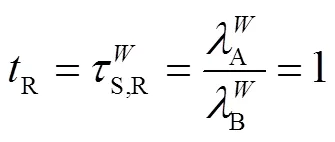

联立(9)和(11)两式,可得:

由DSS分析方法定义,有:
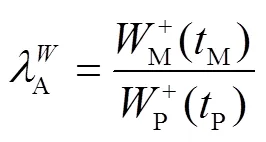


根据膨胀变换准则,有:
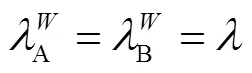

可得:
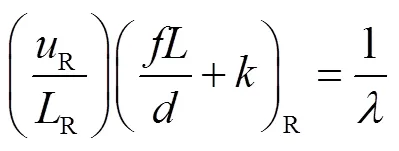

联立(17)、(21)得:

假设:
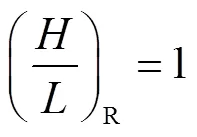
根据膨胀变换相似准则简化式(22):

联立式(20)和(24),有:

自然循环下回路加热段的能量守恒方程为:

当系统处于稳态时,可写为:
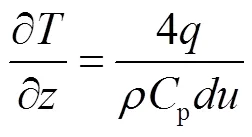
由DSS分析方法,有:
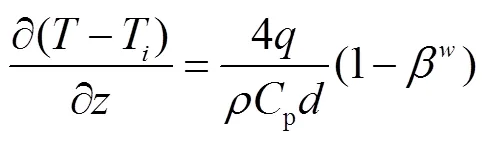
其无量纲形式可以写为:



由DSS比例因子,有:

进一步有:

假设回路热源为点源,则可将式(33)化简为:

再次代入膨胀变换准则:


显然有:
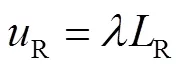
可化简公式(20)为:

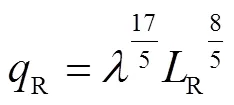
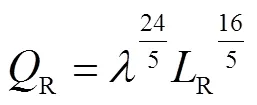
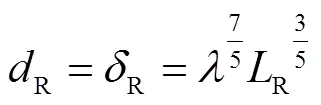
上述各式和式(37)即为膨胀变换方法下的相似准则数组。
显然,文献[10]中基于同一性法所得的相似数组即为上述膨胀数等于1时的对应分析结果。
2 计算及结果分析
基于上述物理模型,建立适用于RELAP5程序计算的节点模型,各构件设置如图3所示。其中,管型部件160P模拟加热段,经由热构件对其进行恒定功率加热;同为管型部件的110P模拟冷却段,采用对流换热方式,110P穿过管型部件210P,210P模拟蒸汽发生器二次侧,通过时间相关控制体200TDV调节210P的流量和温度等参数。174B为分支部件,连接加热管段160P、上部水平管段190P以及由180P和182TVD组成的稳压器部件;各个部件之间由接管SJ进行连接。节点模型的主要参数如表2所示。计算时,首先对关键部件节点数进行敏感性分析。将加热段与冷却段分别划分为5~10个节点,统计回路的稳态流量与冷热段温度表明,不同节点时的计算结果偏差小于3%,因此计算结果与节点数无关[14,15]。
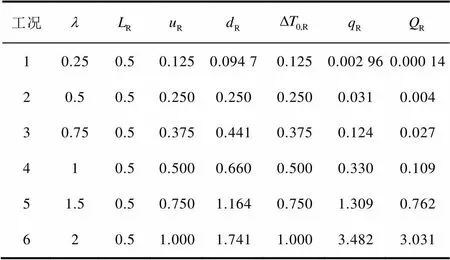
表1 对应于不同膨胀数的相似数组

图2 相似数随膨胀数的变化
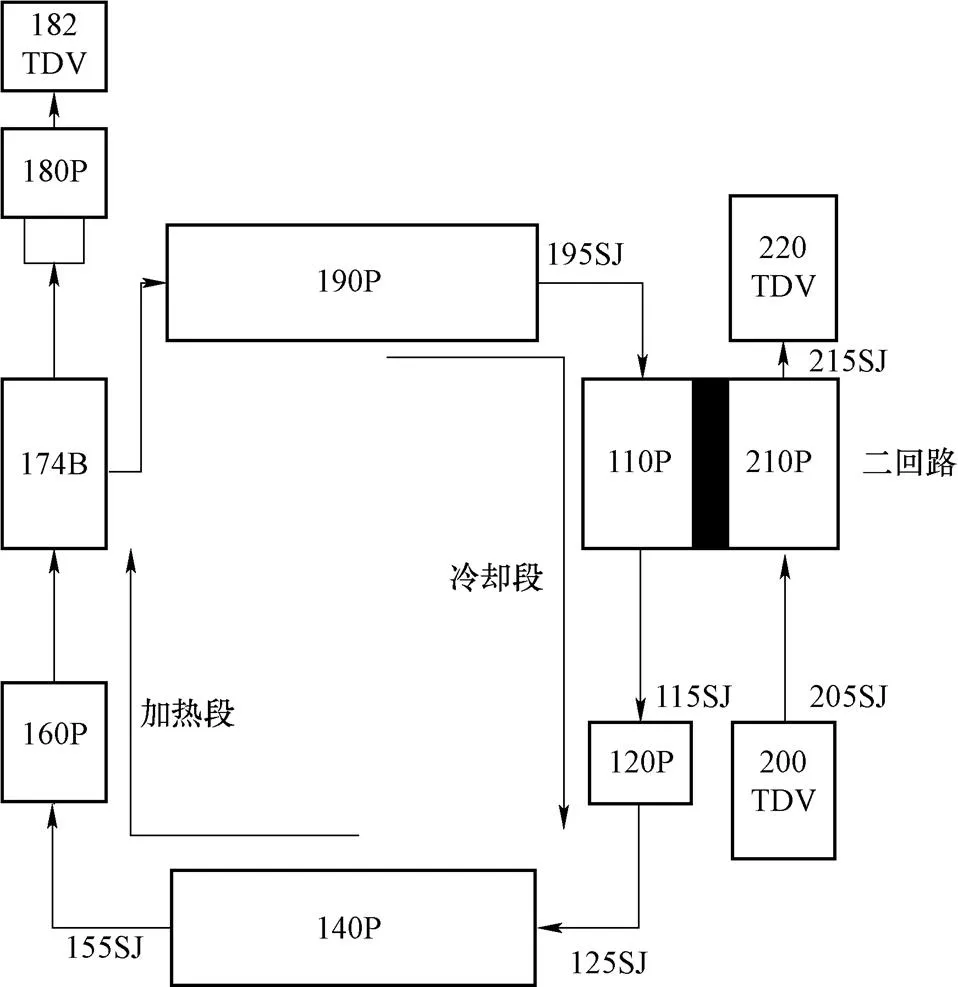
图3 节点划分模型示意图
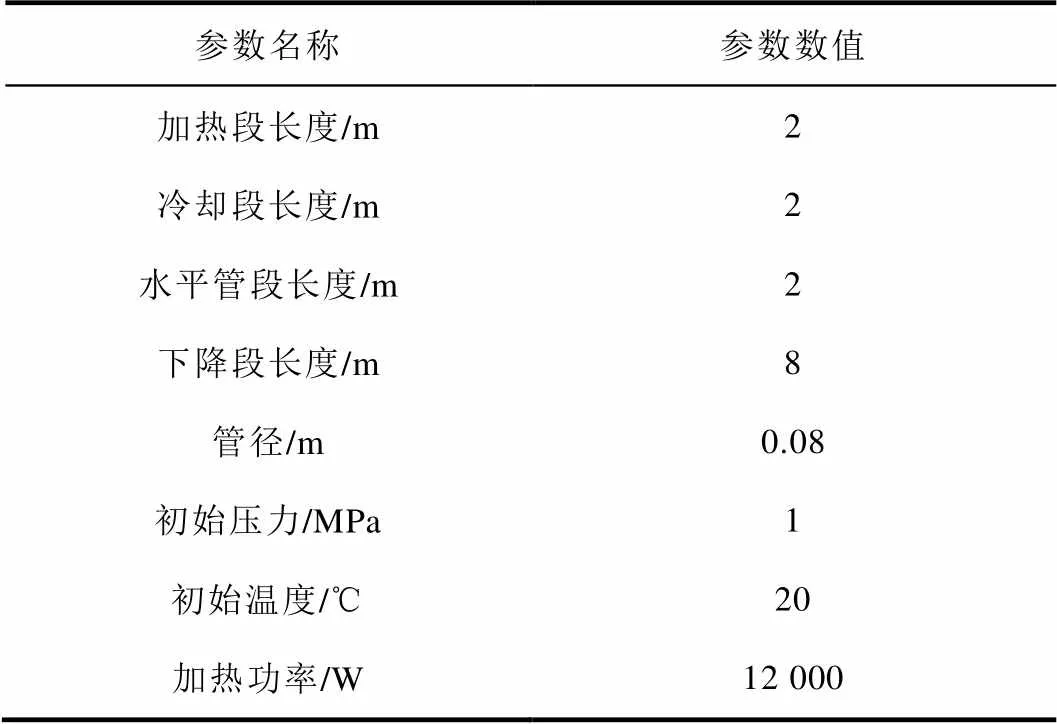
表2 模型(原型)系统参数
为分析系统动态特性,设置了阶跃功率变化,即待系统运行达到稳态后,以阶跃形式将功率提升5%,使系统运行至新的稳态,两个稳态之间的阶段即为动态过程。利用RELAP5程序,分别对原型系统及上述3个工况下的模型系统特性进行了计算,首先对比了各缩比工况与原型工况下关键稳态比例数的相对误差,如表3所示。总体来看,稳态情况下的速度比、温差比的相对误差都比较小,说明此类比例方法是合理的。
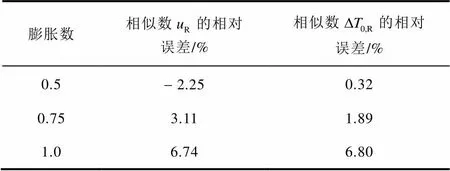
表3 稳态比例数相对误差
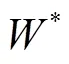
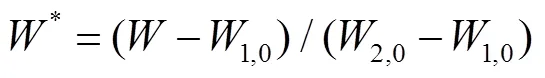
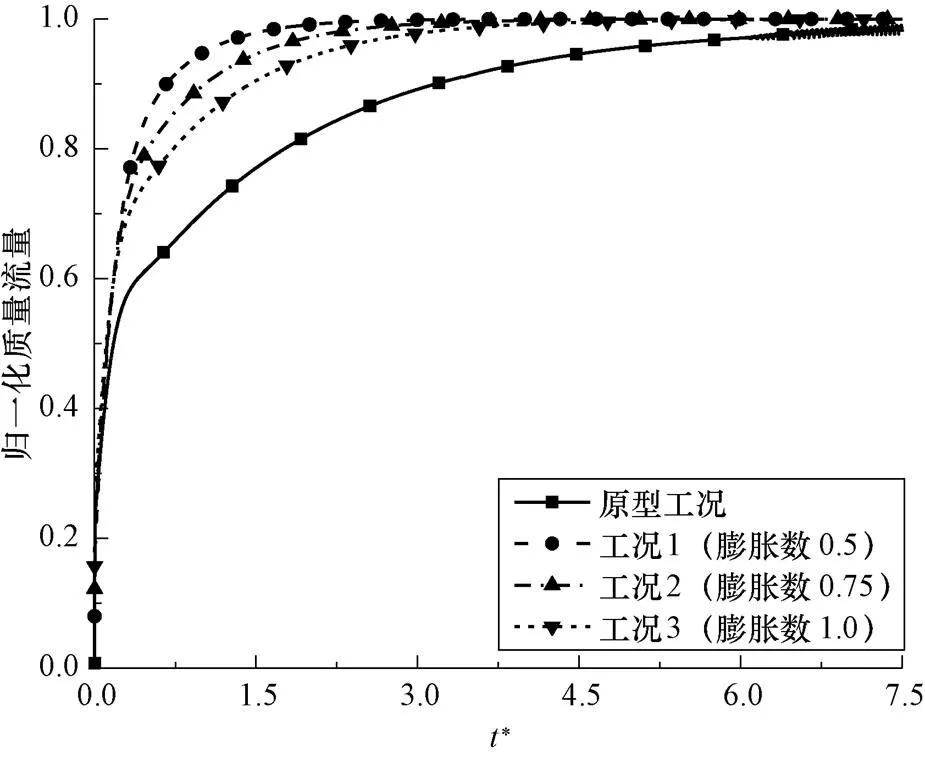
图4 原型与模型的瞬态质量流量变化
横轴则为流体在回路管道内的循环周期。可以看出,在功率瞬间提升时,不同工况下的系统质量流量均会在短时间内迅速上升,随后变化速度开始有所不同:三种缩比工况下,质量流量的上升速率均明显快于原型工况;对比不同膨胀数所对应的工况可以发现,当膨胀数由0.5变化至1.0的过程中,归一化质量流量趋于稳定的速度有放缓的趋势,更加接近原型工况。


图5 各缩比模型瞬态质量流量的相对误差


图6 原型与模型的瞬态冷热段出口温差变化
图7为对应归一化温差的相对误差分布。从总体上看,除了初始阶段外,各个工况下的相对误差均始终保持在±20%以内,且随着时间的增加逐渐趋向于0。在功率跃升的初始阶段,膨胀数0.5、0.75的模型工况波动幅度较大。而当循环周期达到4个之后时,归一化温差误差变化趋于一致。
为和传统H2TS方法进行对比评价,以传统相似准则数Ricardson数、热源数和Stanton数为参照,分析了基于H2TS方法和目前DSS方法所得对应相似准则数的动态变化。对应相似准则数定义如下:
Richardson数:

热源数:

Stanton数:

代入DSS缩比准则,可简化为:


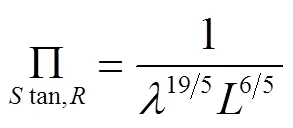
表4列出了膨胀变换下模型和原型之间上述相似准则数的比例关系。显然,和H2TS方法明显不同的是,在DSS方法中,Ricardson数和Stanton数的理论比例都不等于1。

表4 对应于不同膨胀数的相似准则数理论比例
图8~图10分别给出了不同相似准则数随时间变化的动态误差。
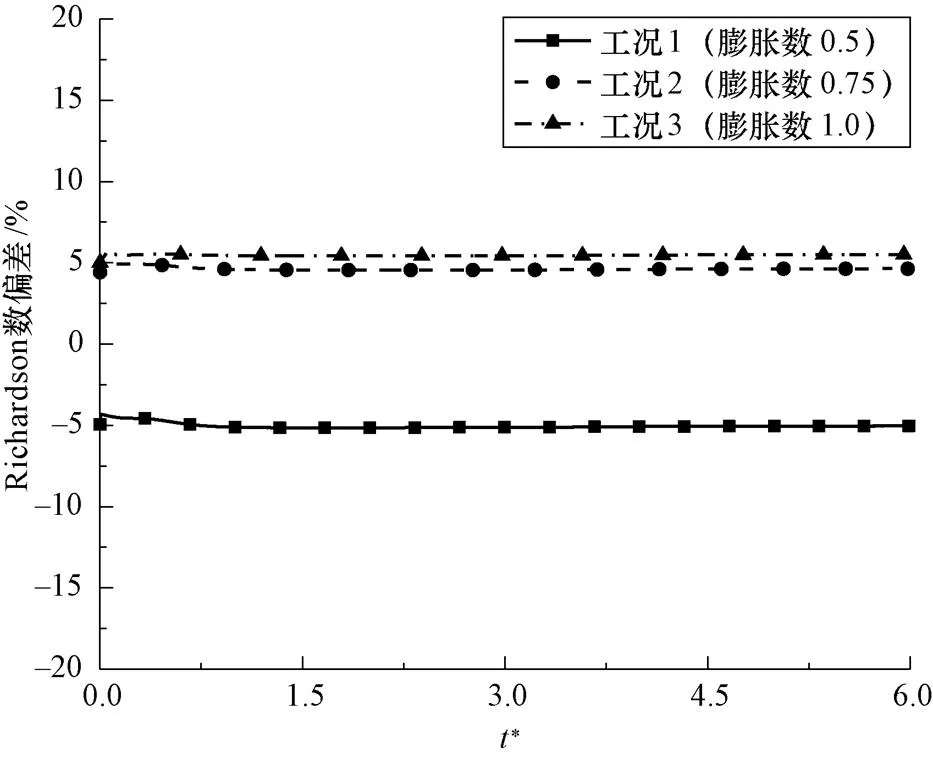
图8 Richardson数的动态偏差
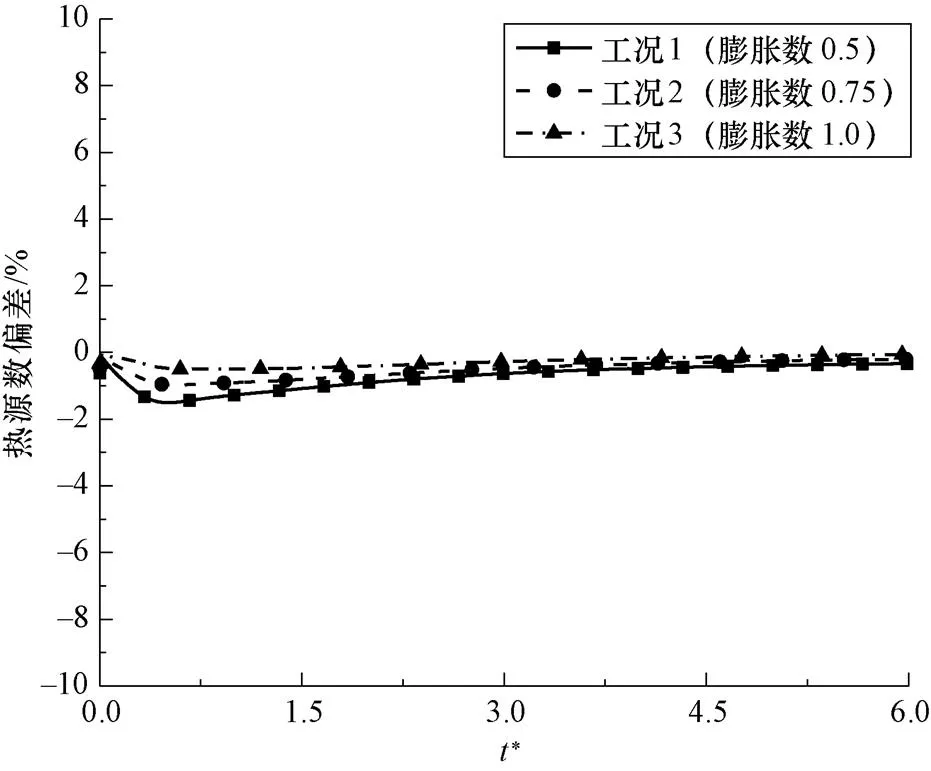
图9 热源数的动态偏差
图8为Richardson数偏差,可以看出,三组缩比工况的误差范围在±10%以内,存在一个合适的膨胀数,可以使缩比模型的理查德森数与原型工况相吻合。图9表示三组缩比工况的热源数误差。从整体上看,不同膨胀数对应的各个缩比工况相较于原型工况的误差都非常小,在±2%以内。且随着膨胀数的增大,误差逐渐减小。Stanton数偏差如图10。三个缩比工况的Stanton数偏差均在±5%以内,且同样存在一个合适的膨胀数,使Stanton数偏差为0。
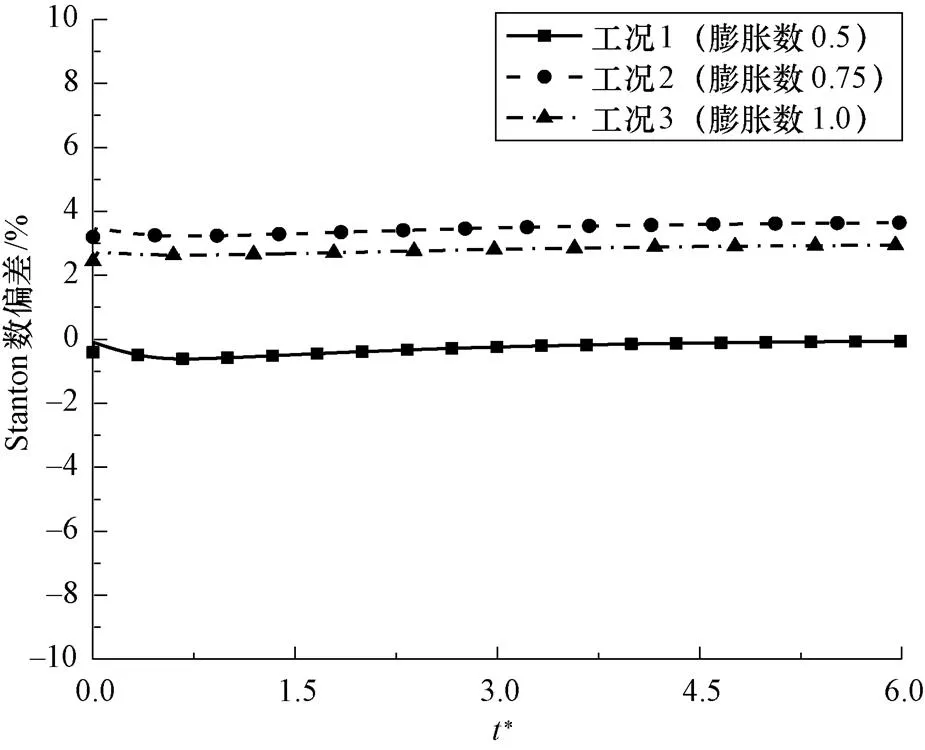
图10 Stanton数的动态偏差

3 结论
以单相自然循环系统为研究对象,推导了单一膨胀参数下的动态比例分析方法,获得了固定长度比例下不同膨胀数所对应的相似数组,利用RELAP5程序计算了简单矩形环路内对应工况时的自然循环特性,并评价了相关偏差。结论如下:
(1)在长度比例不变的情况下,基于不同的膨胀数,可以得到不同的相似数组,对应的相似准则数比均随膨胀数的增大而增大。
(2)对于整个动态过程,三种不同的缩比模型和原型系统的质量流量和冷热段温差的相对误差均在较小范围内;当膨胀数由0.5到1.0增大的过程中,缩比工况的归一化质量流量与归一化温差变化趋势与原型工况逐渐接近,同时,流量与温差的误差逐渐减小。
(3)基于单一膨胀数所得的自然循环相似准则数组中,热源数是决定性准则数,其在不同工况下的相对误差都比较小;而理查森数和斯坦顿数均为非决定性准则数,其在不同工况下的相对误差存在较大的波动范围。
[1] Ishii M,Kataoka. Scaling laws for thermal-hydraulic system under single phase and two-phase natural circulation[J]. Nuclear Engineering and Design,1984,81:411-425.
[2] Reyes Jose N Jr.,Hochreiter L. Scaling analysis for the OSU AP600 test facility(APEX)[J]. Nuclear Engineering and Design,1998,186:53-109.
[3] Zuber N,Wilson G E,Ishii M,et al. Valented. An integrated structure and scaling methodology for severe accident technical resolution:development of methodology[J]. Nuclear Engineering and Design,1998,186:1-21.
[4] Yuquan Li,Huajia Chang,Zishen Ye,et al. Analyses of ACME integral test results on CAP1400 small-break loss of coolant accident transient[J]. Progress in Nuclear Energy,2016,88(1):375-397.
[5] 赵冬建,李胜强,李玉全,等. 一维自然循环比例分析的理论模型[J]. 原子能科学技术,2010,44(08):964- 968.
[6] 赵冬建,李胜强,李玉全,等. 一维自然循环比例分析的结果与讨论[J]. 原子能科学技术,2010,44(08):964-968.
[7] 卢冬华,肖泽军,陈炳德. 压水堆自然循环比例模化基本方程及相似准则数的研究[J]. 核动力工程,2009,30(03):72-84.
[8] Jose N,Reyes Jr.The dynamical system scaling methodology[C]. In:The 16th International Topical Meeting on Nuclear Reactor Thermal Hydraulics(NURETH-16). Chicago,USA,2015.13129.
[9] Xiangbin Li,Nan Li,Qiao Wu,et al. Application of dynamical system scaling method on simple gravity-driven draining process[J]. Journal of Nuclear Science and Technology,2018,55(1):11-18.
[10] Xiangbin Li,YongHao Li,Nan Li,et al. Abdus Samad Muhammad,Sh-iliang Zhou.DSS application on single- phase natural circulation in a simple rectangular loo-p[J]. Annals of Nuclear Energy,2018,119(05):214-228.
[11]李向宾,詹奔腾,王忠毅,等. 简化反应堆一回路系统自然循环的动态比例特性研究[J]. 原子能科学技术,2021,55(08):1386-1394.
[12] The RELAP5 Development Team,1995. RELAP5/MOD3 Code Manual[R],NUREG/CR-5535,INEL-95/0174,1995.
[13] Vijayan P K,Austregesilo H. Scaling laws for single-phase natural circulation loops[J]. Nuclear Engineering & Design,1994,152(1-3):331-347.
[14]邢立淼,郭赟,曾和义. 基于RELAP5的单通道自然循环流动不稳定性分析[J]. 原子能科学技术,2010,44(08):958-963.
[15]刘龙炎. 基于RELAP5的多通道自然循环流动不稳定性分析[D]. 哈尔滨:哈尔滨工程大学,2015.
Study on the Dynamical Scaling Analysis Method of Single-phase Natural Circulation Based on Dilation Transformation
LI Xiangbin1,2,XU Jianing1,2,LIU Yusheng3,YANG Shuai1,2,FENG Mingcong1,2,WU Qiao4
(1. North China Electric Power University,Beijing 102206,China;2. Beijing Key Laboratory of Passive Safety Technology for Nuclear Energy,Beijing 102206,China;3. Nuclear and Radiation Safety Center,Beijing 100082,China; 4. Oregon State University,Corvallis 97331,USA)
In order to further understand the dynamical scaling process, a new dynamical system scaling method based on the dilation transformation is developed. The similarity criteria corresponding to different dilation numbers are obtained under fixed length ratio, the characteristics of single-phase natural circulation in a simple rectangular loop are simulated by using the RELAP5 program, and the internal variation related to key parameters and similarity criteria are analyzed. It is found that the relative errors of the mass flow and the temperature difference between the prototype and model systems are in a small range under most conditions. When the expansion number increases from 0.5 to 1.0, the normalized mass flow rate and normalized temperature difference of the reduced ratio condition are gradually close to those of the prototype condition. At the same time, both the flow error and the temperature difference error gradually decrease. The heat source number is the decisive one among the similarity criteria numbers based on the single dilation number. However, the Richardson number and Stanton number are both non-decisive ones.
Dilation transformation; Dynamical scaling analysis; Single-phase natural circulation; Scaling deviation
TL333
A
0258-0918(2023)05-1064-09
2022-06-24
李向宾(1975—),男,河南洛阳人,副教授,博士,现从事反应堆热工安全方面研究

