自然循环下钠冷快堆中迷宫型节流件水力特性研究
周志伟,曹 锋,陆道纲,曹 琼
自然循环下钠冷快堆中迷宫型节流件水力特性研究
周志伟1,曹锋2,陆道纲2,曹琼2,*
(1. 中国原子能科学研究院,北京 102413;2. 华北电力大学 非能动核能安全技术重点实验室,北京 102206)
迷宫型节流件常被安装在钠冷池式快堆主容器冷却系统、泵冷却系统等流动旁路中,使得进入这些旁路的流量达到设计值,来有效冷却设备,保证快堆的安全。目前国内对自然循环条件下节流件的阻力特性研究较少,本文对迷宫节流件在自然循环和强制循环两种条件下进行了实验和数值研究。首先,实验采用恒定温度(84 ℃)的液态水作为工质,得到了两种循环条件下节流件的阻力系数;其次,对节流件进行数值模拟,将不同湍流模型、壁面法向网格间距下的数值模拟结果与实验结果进行了比较,验证了数值模拟的有效性;最后,通过比较不同湍流模型的计算结果和流场细节,得出适合于两种条件下迷宫式节流件数值模拟的湍流模型,并发现回流漩涡是节流件的主要耗能方式,两种条件下模拟结果的差异主要集中在二次回流区域大小的不同,自然循环下回流区域明显大于强制循环,且收缩速度较慢。
迷宫型节流件;水力特性;湍流模型;数值模拟
钠冷快堆(SFR)具有高效利用铀资源、嬗变长寿命锕系元素和固有安全性等突出优势,是第四代先进核反应堆堆芯之一[1]。在SFR中,迷宫式节流件常常安装在SFR主容器冷却系统、泵冷却系统等流动旁路中,以将旁路中的流量和压降控制在设计范围内,防止出现旁路中流量过大而导致主回路中冷却剂流量不足的事故。因此,准确预测节流件的压降和水力特性对钠冷快堆的安全评估具有重要意义。
Rhode和Sobolik使用有限差分法模拟了矩形齿迷宫密封中可压缩流体的泄漏流[3]。Yang和Luis量化了进口圆角对水润滑密封件的影响。发现弯曲进口密封的进口压降较小,但由于固体颗粒的侵蚀,进口边缘容易磨损[4]。Artur等人优化了带有两个斜翼的直通式迷宫节流件。同时将数值计算结果与实验数据进行了比较,得出位置、倾角和翅片厚度对减少泄漏的影响最大[5]。Zhang等人讨论了涡流制动器对迷宫密封流场和转子动力学性能的影响。结果表明,涡流制动器数量、长度的增加,以及涡流制动器间隙的减小,都会改善直线涡流制动器的转子动力学性能[6]。Wang等人研究了高压控制阀盘中由一系列直角旋转组成的曲折迷宫通道。研究发现,与“平行通道”相比,“串联通道”可以更有效地降低压降[7]。Asok等人分别研究了圆形腔、方形腔和弯曲腔迷宫密封的流动特性。发现空腔内的多个再循环区域促进了动量耗散,从而提高了密封性能[8]。Wang等人分析了轴向位置对阶梯迷宫密封密封性能的影响。结果表明,泄漏和传热特性实际上与轴向位置无关[9]。秦亥琪等对迷宫密封进行了实验和数值研究,得到了其水力特性随密封几何尺寸的变化规律[10]。宋怡等人对迷宫式节流件进行了数值分析,并拟合了压降与几何参数之间的经验关系式[11]。除了数值模拟,关于节流密封的实验也有很多。Dobrowolski等人采用微粒图像测速仪(PIV)观察迷宫密封中的润滑脂流动,评估了迷宫密封中的润滑脂速度分布,发现润滑脂稠度与旋转环转移速度之间存在关系[12]。Untarou等人进行了数值和实验研究,以计算固定直通迷宫密封的流动参数。同时清楚地观察到迷宫密封中的局部流动现象[13]。
综上所述,国内外有许多针对迷宫密封这类细微通道内流动特性的研究,但对节流件这种安装在旁路中的节流元件研究较少。在对反应堆进行热工水力数值仿真时,研究人员往往更关心反应堆堆芯及主回路管道内的流动及传热特性,对节流件这类旁路中的节流元件往往进行忽略或简化。但在自然循环条件下,其阻力特性对整个回路的影响不能忽视。
因此本文将通过实验和数值模拟来研究迷宫节流件在自然循环和强制循环条件下的阻力特性。首先根据实验得到其阻力系数。然后采用不同的湍流模型对节流件进行数值模拟,通过与实验结果进行比较,得出合适的湍流模型。最后,分析节流件在两种条件下流场的差别。
1 迷宫式节流件的水力实验
1.1 迷宫节流件结构及尺寸
三维迷宫式节流件由厚度相同、高度相同且高于管道半径的节流板组成。相邻节流板之间的间距相同,并以180°交错排列。节流部分置于圆管内,示意图如图1所示。

图1 迷宫型节流件示意图[11]
本文研究的节流件由七个节流板组成,两个相邻的节流板是交错的。其具体几何参数如表1所示。横截面如图2所示。

表1 节流件几何参数
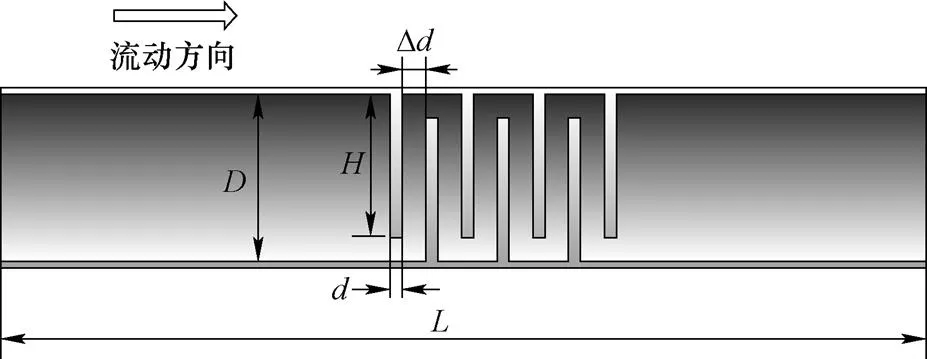
图2 节流件横截面
1.2 实验原理及参数
本实验是研究迷宫节流件流动特性的验证实验。考虑到实验的安全性,本实验用去离子水代替液态钠。为了保持SFR的水力特性,必须完成液态钠和水之间实验参数的相似转换。水力相似转换需要满足几何相似性、运动相似性和动力相似性。
为了满足几何相似性,实验的节流件与钠冷快堆中的迷宫节流件具有完全相同的几何参数。同时,由于液态钠和去离子水都被认为是不可压缩的粘性流体,因此粘性力是控制其流场水力特性的主要作用力。当两个流场的雷诺数相同时,保证了运动相似性和动力相似性。雷诺数()是一个无量纲数,表示粘性流体的惯性力与粘性力之比。
式中:——雷诺数的特征长度,在实际计算中选用节流件的内径;
——流体特征速度,计算中选取入口流速;
钠冷快堆中流经迷宫节流件的液态钠温度为360 ℃。钠的物性参数计算公式如表2所示。由于实验的节流件尺寸完全相等,且在相同的单值条件下,要满足雷诺数相等,即



表2 液态钠物性[14]
在迷宫节流件中,节流板引起的局部阻力是节流件压降的主要来源,根据局部阻力系数公式,管道中流动的压降与阻力系数满足如下关系式:

为局部阻力系数,是雷诺数的单值函数,即
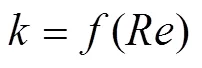
因此,当不同流体的雷诺数相同时,它们的阻力系数也相同。当获得去离子水流经被测节流件产生的压降时,便可根据欧拉相似准则计算液态钠流经同一节流件产生的压降。
欧拉相似准则:

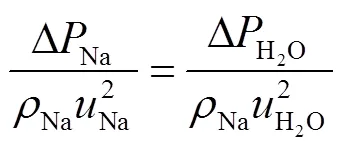
因此,本实验仅需测量被测节流件两侧的水流量和压降。相似转换后的迷宫式节流件水力参数如表3所示。
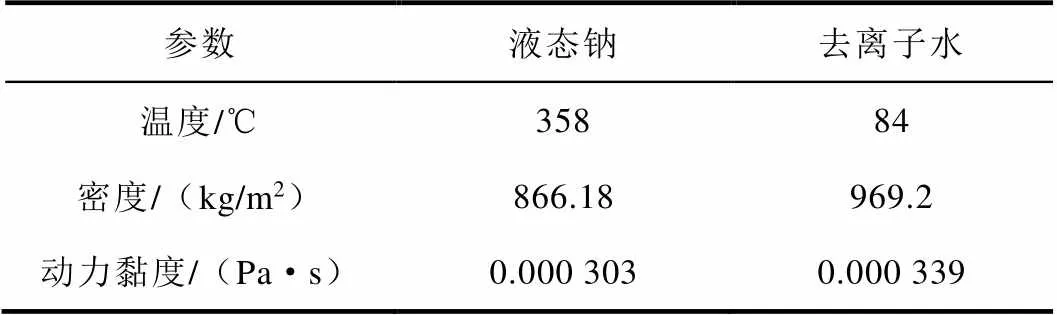
表3 节流件水力参数
1.3 实验装置及流程
整个实验系统由实验回路和加热回路两部分组成。实验回路包括去离子水箱及其出口阀、被测节流件、流量计、压力表、节流进口电动阀、顶部排气阀、变频泵和热电偶。加热回路包括一个额定功率为120 kW(380 V)的筒式加热器,通过入口和出口阀与实验回路相连。系统图如图3所示。
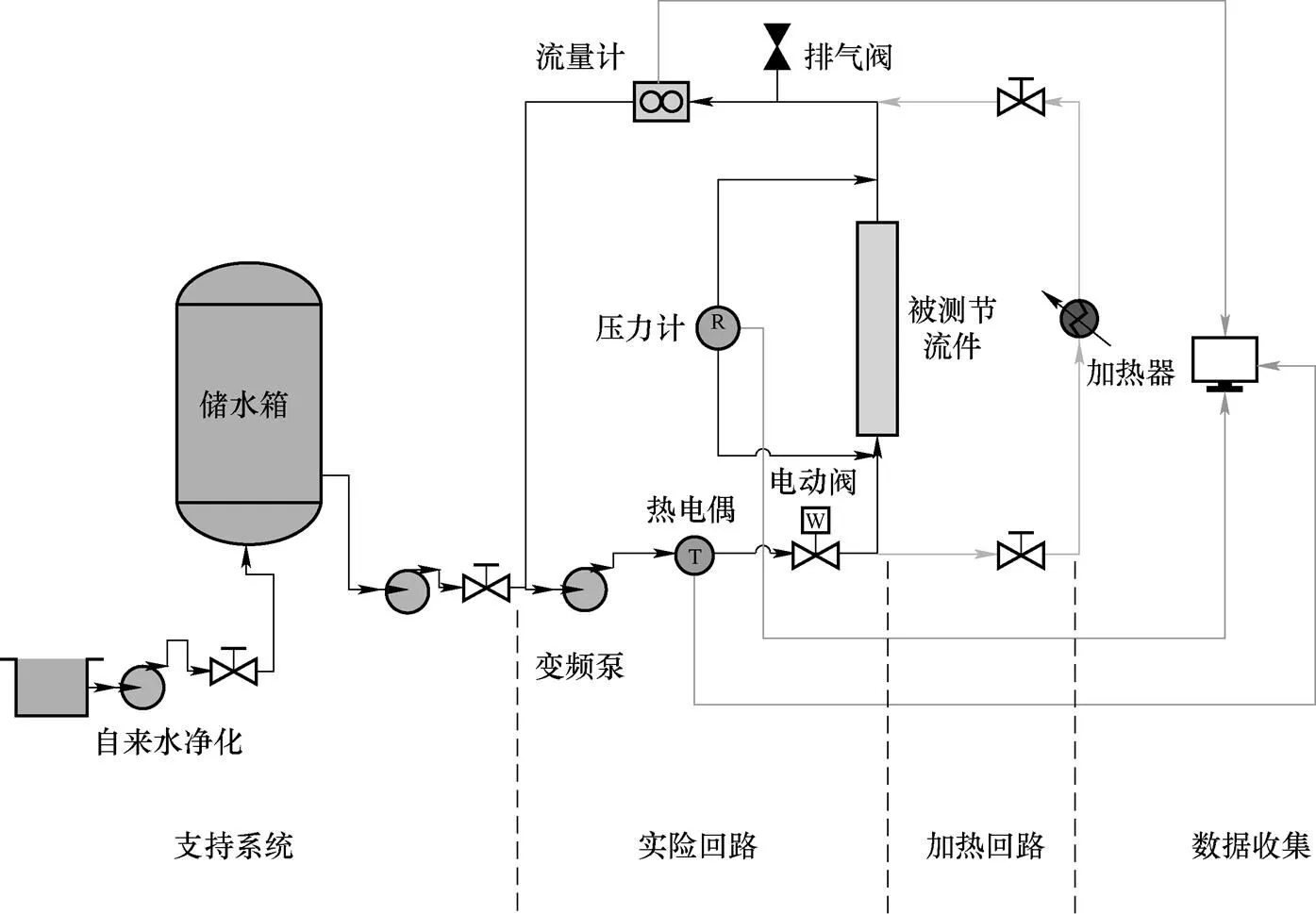
图3 实验回路示意图
试验开始时,打开两个回路中的阀门,变频泵将去离子水从去离子水箱泵入试验系统,直到去离子水完全充满两个回路,然后打开试验回路顶部的排气阀,排出多余的空气。然后,通过水箱出口阀将去离子水箱与测试系统隔离,以防止实验过程中加热的水返回水箱。最后,变频泵驱动去离子水连续通过加热回路和实验回路。由于此时加热回路与实验回路相连,整个实验系统中的水由圆柱形加热器加热,直到达到实验温度要求。去离子水达到所需温度后,关闭加热器,并通过关闭加热回路的入口和出口阀将实验回路与加热回路隔离。整个实验回路全部外覆保温材料,保证在实验过程中去离子水温度保持恒定。
通过改变电动阀的开度,可以精确控制去离子水的流量。被测节流件的额定流量为11.5 kg/s,试验期间进行了两种工况:一种是额定流量的2.5%~6.2%的自然循环工况,另一种是额定流量的75%~110%的强制循环工况。
钠冷快堆正常运行时,通过主泵带动钠冷却剂流动,为强制循环工况。在钠冷快堆停堆时,钠冷却剂依然存在正常流量6%左右的流量来导出堆芯的余热,这种情况即为钠冷快堆的自然循环工况,本实验的试验台架则通过控制去离子水的流量来模拟钠冷快堆的这两种循环工况。
当流量稳定时,由计算机采集流量和压降数据。每个工况持续3~4 min,测量三次。最终结果取平均值。
1.4 实验结果和不确定度
实验测量了5种自然循环工况和12种强制循环工况下被测节流件的流量和压降。结果如图4所示。

图4 压降随质量流量变化的实验结果
实验不确定性有两个来源,包括数据处理和测量设备。对于钠冷却剂,压降和流量的不确定度分别小于1%和3%。热电偶已校准,最大不确定度为±0.5 K。
2 迷宫节流件的数值模拟
2.1 模型和网格化方法
数值模拟的几何模型的大小与实验1:1相同。采用ICEM软件划分非结构化四面体网格,在节流板壁面生成5层边界层网格,靠近壁面的第一个边界层网格厚度为9.7×10-5m。ICEM中节流板处的网格如图5所示。

图5 节流件网格示意图
2.2 边界条件和湍流模型
表4展示了数值模拟的边界条件。自然循环和强制循环条件下水力试验和数值模拟的范围分别为8 124~19 889和244 323~352 796。因此,模拟的液态钠流动属于高雷诺数条件下的湍流。采用雷诺平均(RANS)方法下的五种湍流模型。包括标准-、Realizable-、标准-、Spalart-Allmaras(S-A)和应力剪切传输(SST)对迷宫节流件的流动特性进行了研究,五种湍流模型均采用稳态分析。计算方法选用Simple算法。

表4 边界条件
2.3 网格敏感性分析
采用商业软件Fluent进行数值模拟。在边界层厚度参数相同的情况下,通过改变全局网格参数生成五种数量的网格。在钠冷却剂质量流量不变的情况下,分析了迷宫节流件压降随网格数的变化趋势,如图6所示,当总网格单元数达到786万时,压降增加幅度很小,计算网格的进一步细化并没有改善数值结果。考虑到精度和收敛速度,选择786万个网格单元的计算网格作为工作网格。
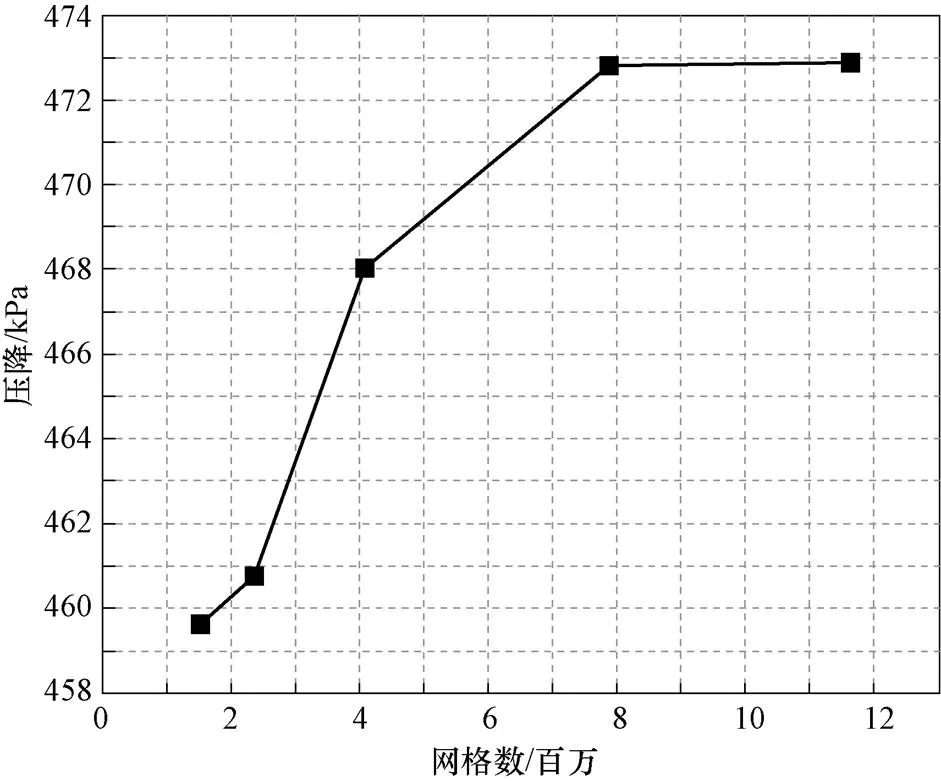
图6 网格敏感性分析
3 迷宫节流件的水力分析
3.1 节流件阻力系数
根据公式(4)可以求得节流件的阻力系数计算公式:

根据公式(8)和实验数据可计算出阻力系数在两种循环条件下随雷诺数的变化。如图7和图8所示,在强迫循环条件下,阻力系数的变化很小,基本稳定在一个恒定的数值,即,。

图8 自然循环下阻力系数随雷诺数的变化
而在自然循环条件下,节流件的阻力系数会随雷诺数的增加逐渐降低,并逐渐趋于平缓,对实验数据进行回归分析,可以得到阻力系数与雷诺数的关系式:
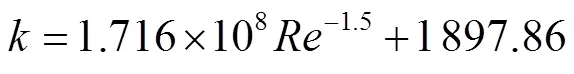
3.2 不同湍流模型的计算比较
3.2.1强制循环条件
图9展示了使用不同湍流模型的计算结果与实验结果之间的比较,在强制循环的高流量下,realizable-的计算结果与实验结果最为吻合。标准-模型、S-A模型和SST模型的计算结果分别比实验值高3.4%~5.42%、5.26%~7.56%和13.97%~18.45%。标准-模型是唯一计算结果低于实验值的模型,比实验值低6.37%~8.19%。因此,建议采用realizable-模型来模拟雷诺数244 323~352 796范围内的迷宫式节流件。
同时当流量为 11.53 kg/s 的额定流量时,realizable-模型模拟的压降为472.7 kPa,与实验结果吻合良好,相对误差仅为0.9%。验证了高流量条件下数值模拟的可靠性。由于SFR的堆芯非常复杂,并非所有的结构设计都能通过实验验证。因此,数值模拟是对实验研究的有效补充。
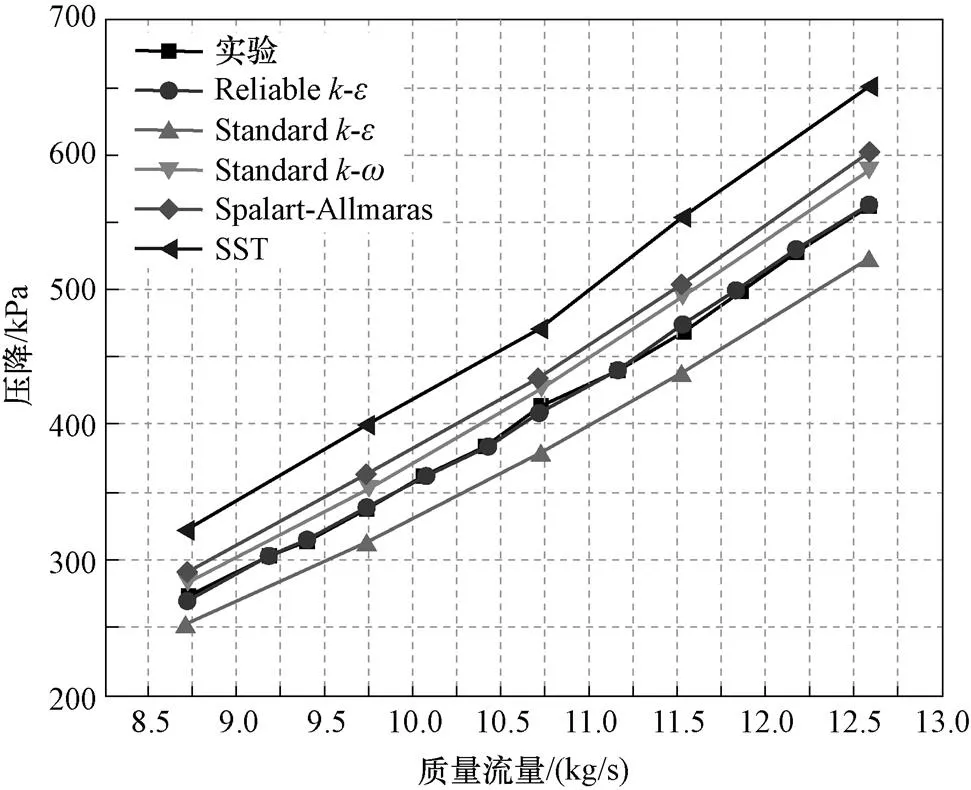
图9 强迫循环条件下不同湍流模型的比较
影响湍流模型计算精度的除了网格数量,还有壁面法向网格距离,常常用无量纲数+表示。+定义为[15]:

——壁面距离。
在图10中,采用realizable-湍流模型在+为10时的数值结果与实验结果吻合良好,而+为30和5的计算结果的平均误差则分别为-3.08%和-1.59%。结果表明,在强迫循环条件下,数值模拟对壁面法向网格距离非常敏感。

图10 realizable k-ε模型采用不同y+值的计算结果比较
3.2.2自然循环条件
图11为自然循环条件下不同湍流模型的计算结果,图12是其各种湍流模型的计算误差。如图11和图12所示,自然循环下五种湍流模型的表现与强迫循环下略有不同。首先,realizable-模型的计算精度降低;同时,标准-模型的精度有提高,误差保持在5%以内;SST和标准-与实验值仍有较大误差。但随着流量的减小,SST模型的计算精度有提高的趋势,而标准-模型的计算精度进一步降低。这是因为随着流速的降低,湍流的壁面粘性变得越来越突出,而在高流速下,壁面分子粘性并不明显。因此流量的降低使得像SST等对近壁面剪切流动有更好模拟效果的湍流模型具有小的误差。

图11 自然循环条件下不同湍流模型的比较

图12 自然循环条件下不同湍流模型的计算误差
对于+的测试,采用低流量下表现最好的标准-湍流模型。如图13所示,当流量大于0.4 kg/s时,+=30更合适,而当流量小于0.4 kg/s时,只有+=10的误差可以在3%以内。

图13 标准k-w模型采用不同y+值的计算结果比较
3.3 节流件流场特性分析
在迷宫型节流件中,液体钠流依次被节流板阻挡,其中一部分可用压头被转换为动能。随后,动能被湍流涡旋消散并转化为热能[16]。为了直观的分析流体速度场,创建了两个通过轴线且相互垂直的截面,截面和截面。两个剖面图如图14所示。
图15显示了额定流量为11.5kg/s下截面上的压力和流速等值线。如图15(a)所示,当钠冷却剂依次流过节流板时,压力逐渐降低,流速周期性变化。每当液态钠流经节流板顶部时,其压力就会急剧下降,每个节流板顶部都会出现一定的低压区域,但两个节流板之间的间隙中压力则变化不大。如图15(b)所示,每个节流板间隙间的速度分布类似,均存在一个低流速区域,其中第一个间隙最为特殊,其低速区域明显大于后续的节流板,同时第一个间隙间的最大速度也低于后续间隙中的最大速度。而在后续的间隙中,因为流道的180°转向,液态钠会冲击下一个节流板的底部,最大流速便出现在冲击处。在每个间隙的中间区域,流速会出现明显分层现象。

图14 XY截面和ZX截面
图16显示了从垂直于截面和截面的角度观察到的三维流线。从图16(a)中可以看出,在每个节流板间隙中,液态钠将形成湍流漩涡。由于节流件流道复杂曲折,涡流不是简单的纵向湍流涡流或横向二次流,而是类似两者的组合。如图16(b)所示,每当液态钠流经一个节流板的顶部时,由于流动截面的缩小和下一个节流板的阻挡,液态钠向两侧扩散,形成横向的漩涡。

图15 XY界面上压力和速度云图

图16 节流件流线图
然而,结合图16(a),在液态钠横向扩散时,它也也会形成纵向的漩涡。这两股流动叠加在节流板间隙中,形成两个倾斜的漩涡。这两个漩涡便是形成间隙间低流速区域及流速分层的主要原因。
3.4 两种循环条件下流场比较
图17显示了低流量0.29 kg/s和额定流量11.53 kg/s之间的流速等值线云图比较。正如之前的讨论,每个节流板顶部后面都会有回流区域。如图17(a)所示,强迫循环条件下,第一个节流板后的回流较大,几乎占据整个节流板的后侧。从第二个节流板开始,回流区域迅速减少,并一直维持到最后一个节流板。而在自然循环条件下,尽管每个节流板后仍有回流,但这些区域不会很快收缩。如图17(b)所示,在第二个和第三个节流板后面仍然有一个比较大的回流区域。同时从图17(c)和图17(d)还可以看出,低流量下的速度场更加无序,每个间隙之间的主流区域更小。这表明在低流速下,壁面对流动的扰动更为显著。这也使得对于边界层流动和低雷诺数流动具有良好模拟精度的标准-模型在自然循环下具有更好的精度。
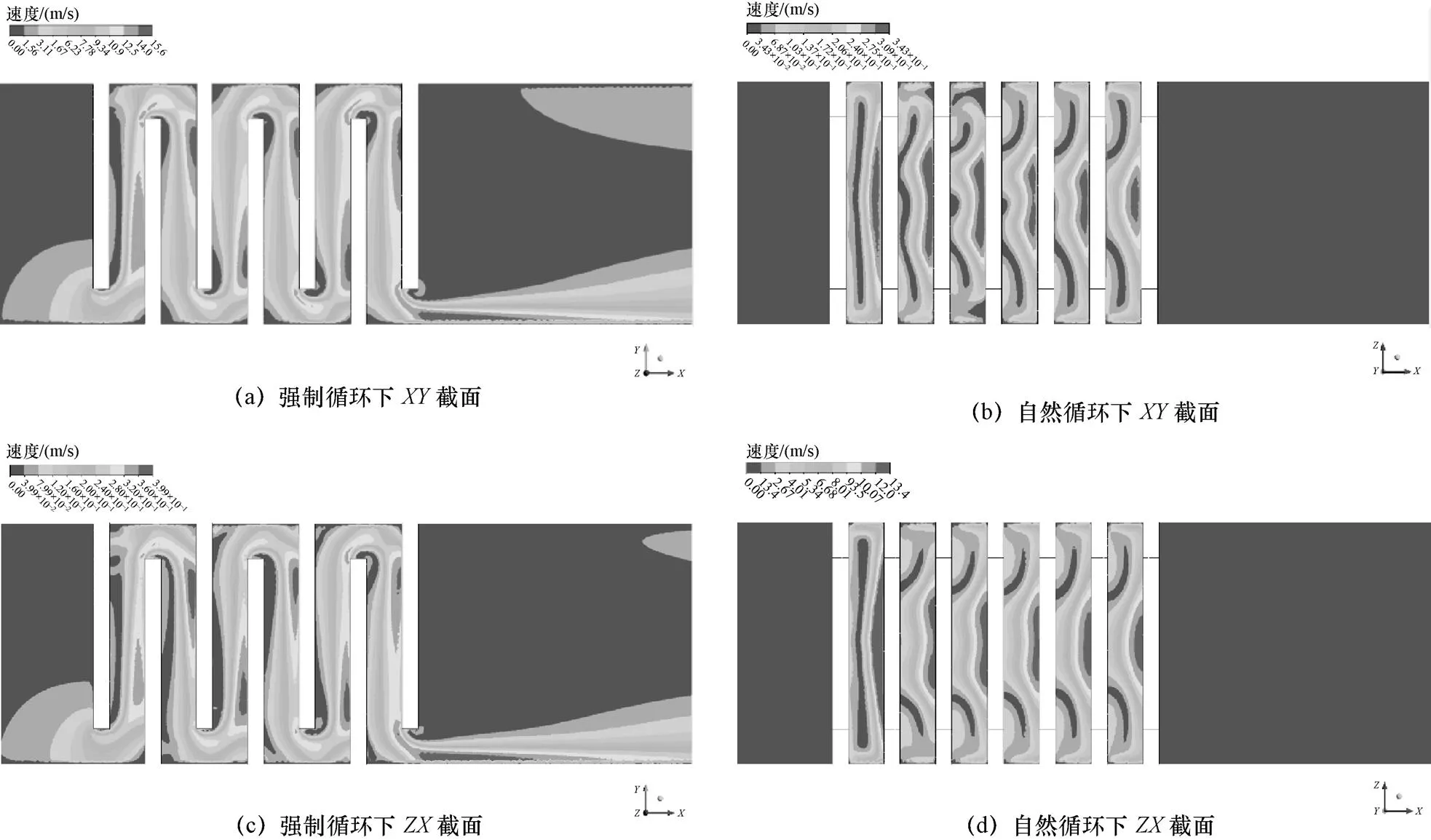
图17 流场速度云图
4 结论
在本论文中,对迷宫节流件在自然和强制循环条件下进行了实验和数值研究,得出以下结论。
(1)通过水力试验,获得节流件在自然循环条件下阻力系数与雷诺数的关系式,同时得到在强制循环条件下,节流件的阻力系数稳定在144.17左右。
(2)对节流件在两种循环条件下进行数值模拟,通过与实验结果的比较,推荐壁面法向网格间距+的取值为10。同时得出Realizable-湍流模型在强迫循环下具有最好的计算精度,而标准的-湍流模型在自然循环下具有最好的计算精度。
(3)节流板间隙内的倾斜湍流漩涡引起的能量耗散是节流件产生压降的主要原因。同时,漩涡使每个节流板的在后侧形成低速回流区域。回流区域会随着流体不断经过节流板而逐渐缩小。
(4)两种循环条件下模拟结果的差异主要集中在二次回流区域大小的不同。在自然循环的低流量下,各节流板后的回流区域明显大于高流量下的回流区域,且收缩速度较慢。
[1] USDOE.A Technology Roadmap for Generation IV Nuclear Energy Systems[R]. 2002:239-241.
[2] Fang X,Wang Y Z,Diao A N,et al.Structural Optimization Design of Labyrinth Seal Based on Software FLUENT[J]. Fluid Machinery,2013.
[3] Rhode D L,Sobolik S R.Simulation of Subsonic Flow Through a Generic Labyrinth Seal Cavity[C]. Asme International Gas Turbine Conference & Exhibit.American Society of Mechanical Engineers,1985.
[4] Jing Y,Luis S A.On the Influence of the Entrance Section on the Rotordynamic Performance of a Pump Seal with Uniform clearance:a Sharp Edge VS.a Round Inlet[J]. Journal of Engineering for Gas Turbines & Power,2018.
[5] Szymanski A,Wroblewski W,Fraczek D,et al. Optimization of the Straight-Through Labyrinth Seal With a Smooth Land[J]. Journal of Engineering for Gas Turbines & Power,2018,140(12):122503.1-122503.9.
[6] Zhang W,Wu K,Gu C,et al.Swirl Brakes Optimization for Rotordynamic Performance Improvement of Labyrinth Seals Using Computational Fluid Dynamics Method[J]. Tribology International,2021,159(2):106990.
[7] Hai-min,WANG,Yue,et al.Numerical simulation of flow characteristics for a labyrinth passage in a pressure valve[J]. 水动力学研究与进展:英文版,2016(4):8.
[8] Asok S P,Sankaranarayanasamy K,Sundararajan T,et al.Neural network and CFD-based optimisation of square cavity and curved cavity static labyrinth seals[J]. Tribology International,2007,40(7):1204-1216.
[9] Wang D,Shi C,Cai X.Numerical calculation of the influence of axial position on the performance of stepped labyrinth seals[C]. 6TH INTERNATIONAL CONFERENCE ON COMPUTER-AIDED DESIGN,MANUFACTURING,MODELING AND SIMULATION(CDMMS 2018),2018.
[10] Qin H,Lu D,Zhong D,et al.Experimental and numerical investigation for the geometrical parameters effect on the labyrinth-seal flow characteristics of fast reactor fuel assembly[J]. Annals of nuclear energy,2020,135(Jan.):106964.1-106964.14.
[11]宋怡,陆道纲,秦亥琦,等.迷宫型节流件压降的数值模拟研究[J]. 核科学与工程,2020,40(2):9.
[12] Duenas Dobrowolski J,Gawliński,Marek,Paszkowski M,et al.Experimental Study of Lubricating Grease Flow inside the Gap of a Labyrinth Seal Using Microparticle Image Velocimetry[J]. Tribology Transactions,2016:1-10.
[13] Untaroiu A,Goyne C P,Untaroiu C D,et al.Computational Modeling and Experimental Investigation of Static Straight-Through Labyrinth Seals[C]. Asme International Mechanical Engineering Congress & Exposition,2008.
[14] Liu Y Z.Investigation on the flow and temperature fields of coolant in a fuel subassembly foe sodium cooled fast reactor[J]. China Institute of Atomic Energy,2007.
[15] Jing C,Zhang D,Ping S,et al.CFD investigation on thermal-hydraulic behaviors of a wire-wrapped fuel subassembly for sodium-cooled fast reactor[J]. Annals of Nuclear Energy,2018,113:256-269.
[16] Rhode D L,Sobolik S R.Simulation of Subsonic Flow Through a Generic Labyrinth Seal Cavity[C]. Asme International Gas Turbine Conference & Exhibit.American Society of Mechanical Engineers,1985.
Study on Hydraulic Characteristics of Labyrinth Throttle in Sodium Cooled Fast Reactor under Natural Circulation
ZHOU Zhiwei1,CAO Feng2,LU Daogang2,CAO Qiong2,*
(1. China institute of atomic energy,Beijing 102413,China;2. Beijing Key Laboratory of Passive Safety Technology for Nuclear Energy,North China Electric Power University,Beijing 102206,China)
Labyrinth throttles are often installed in the flow bypass of the main vessel cooling system and pump cooling system of sodium cooled pool fast reactor, so that the flow entering these bypass reaches the design value, so as to effectively cool the equipment and ensure the safety of fast reactor. At present, there are few domestic research on the resistance characteristics of throttle under natural circulation.Therefore, this paper makes experimental and numerical research on labyrinth throttle under natural circulation and forced circulation. In the experiment, liquid water with constant temperature(84 ℃)was used as the working medium, and the resistance coefficients of throttling parts under two cycle conditions were obtained.Then, the throttle is numerically simulated, and the numerical simulation results under different turbulence models and the normal grid spacing of the wall are compared with the experimental results, which verifies the validity of the numerical simulation.By comparing the calculation results and flow field details of different turbulence models, a turbulence model suitable for the numerical simulation of labyrinth throttle under two conditions is obtained.At the same time, the difference of the flow field of the throttle under the two conditions is compared.It is found that the reflux vortex is the main energy consumption mode of the throttle, and the difference of the simulation results under the two conditions is mainly concentrated in the size of the secondary reflux area.Under natural circulation, the reflux area is significantly larger than that under forced circulation, and the contraction speed is slow.
Labyrinth throttle; Hydraulic characteristics; Turbulence model; Numerical simulation
TL48
A
0258-0918(2023)05-0979-10
2022-06-27
周志伟(1986—),男,湖南邵阳人,博士研究生,现从事核反应堆热工水力学方面研究
曹 琼,E-mail:Caoqiong@ncepu.edu.cn

