基于三维变分算法的蒸汽发生器模型同化方法研究
张 琪,杨淑涵,孙培伟,魏新宇,邱磊磊
基于三维变分算法的蒸汽发生器模型同化方法研究
张琪,杨淑涵,孙培伟*,魏新宇,邱磊磊
(西安交通大学核科学与技术学院,陕西 西安 710049)
蒸汽发生器在实际运行过程中系统参数会发生改变。为保证蒸汽发生器模型能够真实反映蒸汽发生器的实际状态,以蒸汽发生器水位、蒸汽压力、一次侧冷却剂出口温度以及循环流量等观测变量,进行基于三维变分算法的蒸汽发生器模型同化多种蒸汽发生器观测数据的方法研究。对蒸汽发生器仿真模型进行不确定性分析以确定参数调整范围,基于SOBOL算法的敏感性分析结果选择待优化参数组合,拟合关键参数与观测变量之间的函数关系式作为观测数据与模型的耦合方式,最后利用优化算法求解获得了最优参数组合,实现了蒸汽发生器模型的数据同化。通过模型计算值与观测数据对比,结果表明该方法可使蒸汽发生器的仿真精度明显提高,证明了本文方法的正确性。
数据同化;蒸汽发生器模型;三维变分算法;不确定分析;敏感性分析
在压水堆核电厂中,蒸汽发生器的安全运行和控制对整个核电厂的运行安全起着至关重要的作用。据统计,约25%的压水堆紧急停堆均由不良的蒸汽发生器水位控制引起[1,2]。蒸汽发生器仿真模型是研究真实蒸汽发生器热工水力动态特性的重要工具,广泛应用于蒸汽发生器水位控制系统设计中,在水位控制系统设计中起到了巨大作用。因此在对发生器系统进行模拟时,精确的蒸汽发生器模型可以准确反映核电厂蒸汽发生器在实际运行时系统参数的动态变化过程,为操作员的调节提供指导和帮助。然而蒸汽发生器在长期的运行过程中系统参数会发生变化,因此不能忽视模型参数的不确定性对模型的仿真结果的影响,有必要研究数据同化方法,采用测量数据,自动校正模型的相关参数,保证模型能真实反映实际蒸汽发生器的实际运行状态。这对设计合理的蒸汽发生器液位控制系统以及对于核电厂的安全稳定运行具有十分重要意义。
数据同化是一种将观测数据和数学模型相结合,将观测数据融入仿真模型对模型的初始条件和参数进行调整,以实现更好预测的方法。数据同化最初应用于气象、水文等领域,近年来在核工程领域也有广泛应用。Khalik[3]等建立了一个具有敏感性分析、不确定性量化和数据同化的集成框架,该框架可用于对具有大量输入和输出数据流的核模型进行最佳估计计算。Bouriquet和Argaud[4]等提出了一种对核质量进行最优评价方法,该方法对实验数据和数值模型信息可对整合与评估后,进而对核质量进行调整,结果表明调整后的核质量冗余明显降低。Eleveld[5]等为了改进核应急管理系统,对大气弥散模型的数据同化方法进行了试点研究,结果表明核事故早期和晚期潜在污染区域的预测效果显著提高。Bouriquet[6,7]利用三维变分算法和最佳无偏估计对测量网络进行了优化设计,以重建900 MW压水堆堆芯中子通量和功率场。Gong[8]等人提出了一种基于反距离拟合项的3D-Var数据同化方法,结果表明与已有的数据同化方法相比,该方法具有效果较好。Wan[9]等人提出了一种连续能量横截面库的核数据校正方法,通过核数据校正,实验装置的理论“模拟值”与相应的测量值吻合较好。
目前数据同化在核工程领域的成功应用主要集中于反应堆堆芯和核事故应急管理两方面,在核动力装置方向的研究很少。本文以蒸汽发生器为研究对象,基于三维变分算法,采用序列二次规划算法对模型中的关键状态进行优化调整,实现了针对蒸汽发生器的水位、循环流量、冷却剂出口温度和母管蒸汽压力等多种观测数据的同化,并验证了蒸汽发生器模型同化方法的正确性。
1 模拟方法
1.1 蒸汽发生器模型
本文以“华龙一号”核电厂的蒸汽发生器为研究对象,由于无法获得核电厂蒸汽发生器实际运行数据,因此依据真实蒸汽发生器的结构,采用系统程序RELAP5进行建模,并以此模型作为虚拟蒸汽发生器代替真实蒸汽发生器。
RELAP5是目前在轻水反应堆瞬态事故分析中最常用最典型的热工水力分析程序,世界各国都对它做了很多验证工作并生成了最少27篇报告。这些报告均使用真实有效的数据,根据实验数据和RELAP5的计算结果比对,评估程序计算结果的精确性,使最佳估算程序在事故分析和安全分析中的应用得到普遍认可[10]。因此蒸汽发生器的RELAP5模型可以反映实际蒸汽发生器的特性,模型输出可以代替真实的观测数据。RELAP5模型节点如图1所示,一次侧冷却剂进入入口水室后向上流动,流进U型管内,将热量传递给二次侧流体后,从出口水室流出;二次侧给水从给水室向下流动,经过下降段,进入蒸汽发生器管束区被加热而变成蒸汽,蒸汽继续向上流动,在汽水分离器和干燥器中分离出饱和水的后从上封头流出,经蒸汽母管到达汽轮机做功,被分离出的饱和水返回到再循环水室进行下一次循环流动。观测数据选择的是一次侧冷却剂出口温度,二次侧蒸汽发生器水位、循环流量和蒸汽母管压力。
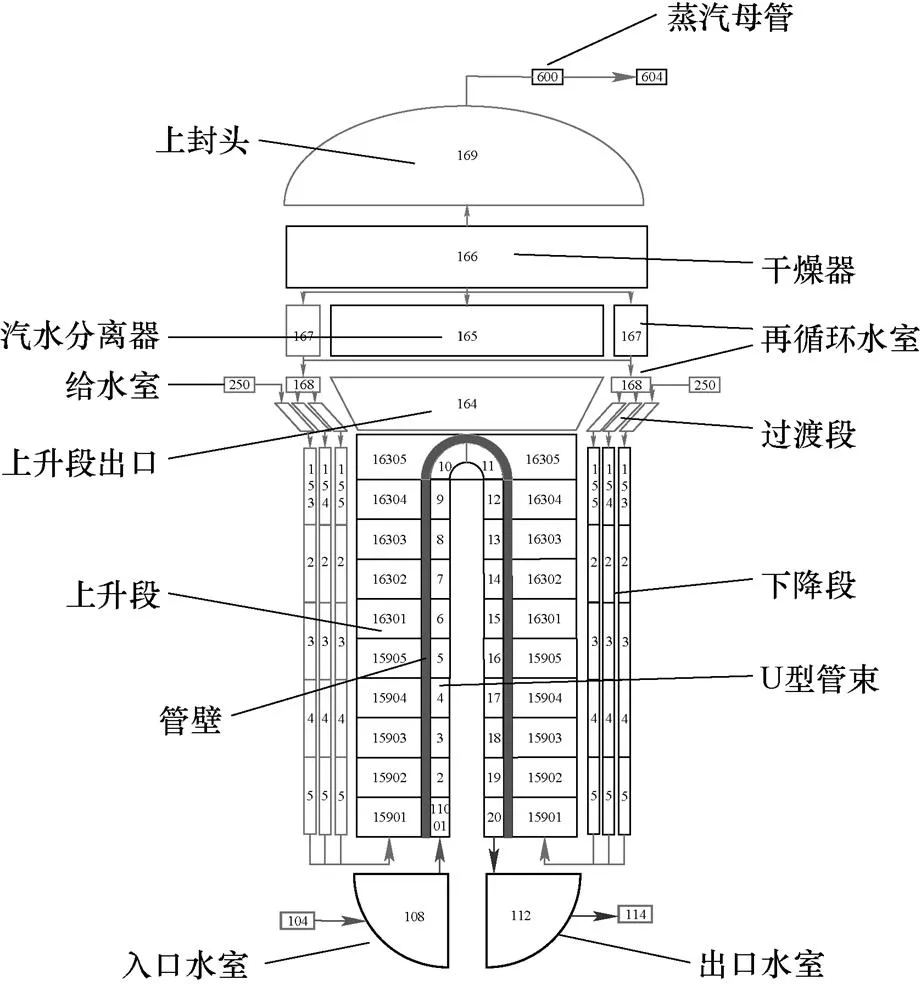
图1 基于RELAP5的虚拟蒸汽发生器
1.2 蒸汽发生器仿真机
基于MATLAB/Simulink仿真平台,依据质量、能量和动量守恒定理和可移动边界理论,建立蒸汽发生器仿真模型,使用该模型实现与RELAP5模型产生的观测数据进行同化方法研究。Simulink模型的节点如图2所示,其中图中节点编号P代表一次侧,S代表二次侧,M代表管壁。

图2 Simulink蒸汽发生器模型
1.3 三维变分算法
三维变分算法是一种数据同化方法,它通过构建代价函数来描述模型计算值和观测值的差异,对代价函数进行求解来获得极小值。基于变分思想,把模型参数的优化问题转化为一个极值求解的问题,在满足约束的条件下,最小化模型计算值与观测值之间的“距离”,使距离最小化的参数即为最优参数。三维变分算法代价函数如下:
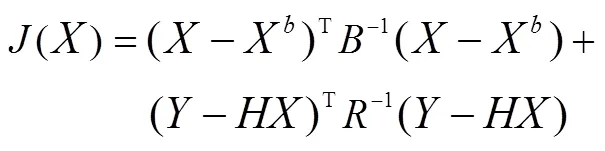
式中:()——代价函数;
——待求解参数;
X——已知参数;
——背景误差协方差矩阵;
——观测数据;
——模型参数与观测数据的映射关系;
——观测误差协方差矩阵。
1.4 研究流程
实际蒸汽发生器在运行过程中重点关注变量有水位、循环流量、冷却剂出口温度和母管蒸汽压力等,选取RELAP5模型中这四个变量为观测值对Simulink模型参数进行同化,在最小化代价函数之前,需要确定,,等变量,同化流程图如图3所示。
同化步骤为:
(1)模型的不确定性分析。假设模型参数的可调整范围,采用广义似然度不确定性分析,计算模型后验分布和模型不确定度,确定模型参数调整的可行性;
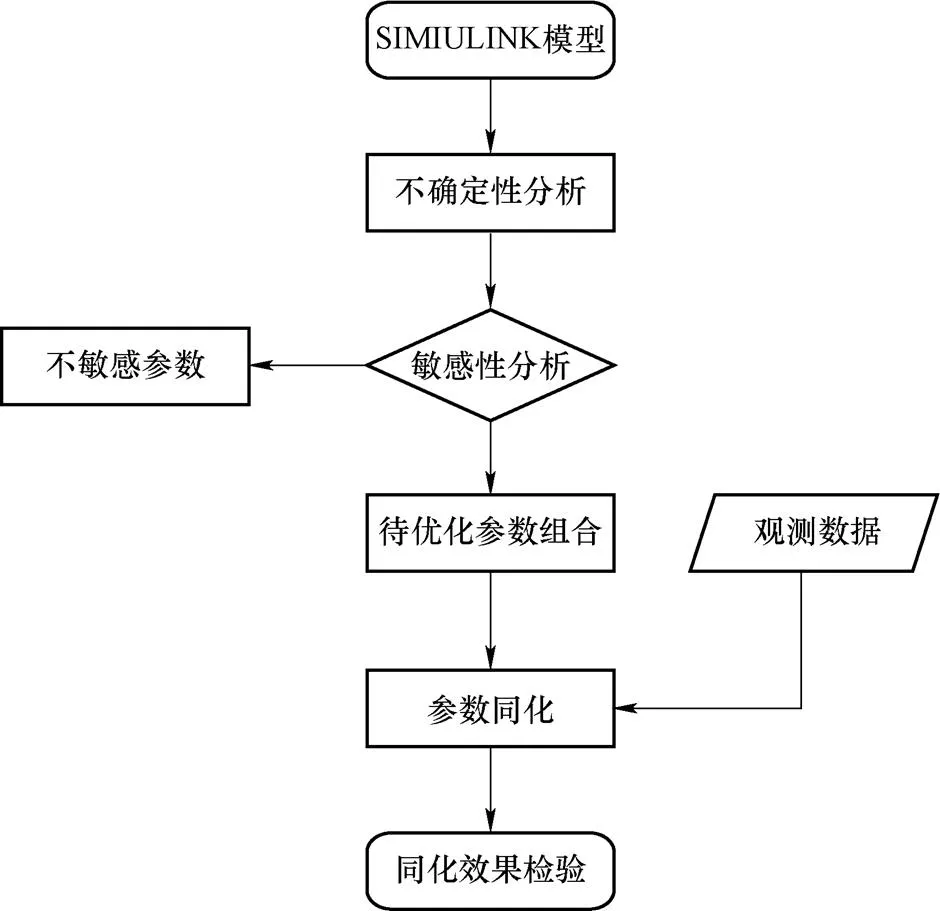
图3 同化流程图
(2)敏感性分析。利用SOBOL算法对Simulink蒸汽发生器模型参数进行敏感性分析,为模型与观测数据同化中的待优化参数的选择提供依据。在敏感参数中,根据参数敏感度,实际物理意义以及尽量少参数的原则获取参数组合;
(3)观测算子的确定。使用Simulink模型,引入待优化参数扰动计算获得观测数据数值,通过函数拟合的方法获得观测算子;
(4)参数优化和效果检验。将计算获得的协方差矩阵代价函数,采用最优化算法求解代价函数最小值。针对已确定的模型参数组合,利用Simulink模型计算获得模拟结果与观测数据进行对比和验证。
2 模型不确定性分析
广义似然度不确定性分析[11](GLUE)是一种通用似然不确定性估计方法,该方法认为模型模拟结果的好坏应由模型参数组合决定,而不是单个参数。
2.1 模型参数选择
模型计算中采用的换热实验公式都存在不确定度,常常可达±20%或±25%[12],Simulink模型沸腾段采用的Chen换热式的计算结果误差甚至达到±50%[13]。阻力系数的不确定度对于模型计算结果的影响也不能忽视。根据蒸汽发生器的热工水力过程以及蒸汽发生器Simulink模型的节点划分,研究所选择的主要模型参数、物理意义及其假设取值范围如表1所示,由关系式计算所得数值乘以该修正因子就是模型参数的变化范围。

表1 主要模型参数的意义及区间
2.2 不确定实验设计
针对蒸汽发生器Simulink模型的换热系数修正因子与阻力系数修正因子的不确定性研究,所采用实验步骤如下:
(1)利用拉丁超立方(LHS)分层抽样方法对每个模型参数进行均匀采样,对各参数进行随机组合,样本组合为5 000组。


式中:——参数组对应的NS值;
——参数组的取值;
S——参数组在时刻对应的Simulink模型输出值,m;
O——时刻RELAP5模型输出值,m;
——仿真总步长,s。
(3)构建参数后验分布和统计。排除步骤(2)中计算结果低于指定阈值的参数组,对高于指定阈值的参数组合进行归一化,利用归一化结果统计各参数的后验概率密度分布。
(4)对步骤(3)中筛选出的参数组对应的模型模拟值进行排序,计算累计似然分布的5%和95%分位数,利用分位数结果获得模拟水位的90%不确定性区间并计算不确定区间宽度,评估参数与仿真结果不确定性之间的关系:

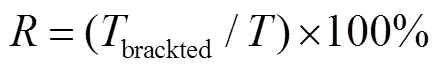
式中:——不确定区间宽度,m;
——总时间步长,s;
——覆盖度;
bracketed——位于90%置信区间的实测步长,s。
2.3 参数后验分布与不确定区间
若某参数对纳什系数无明显影响,则参数的似然分布应与初始假设分布尽可能一致;若影响较大,则参数的似然分布与初始假设分布相差较大,呈正态分布。各模型参数的后验分布如图4(a)~图4(h)所示。由图可知,KR1、KR3、KR4和KR5的后验分布呈近似均匀分布与所选的先验分布基本相同,表明这4个参数对模型的输出影响不明显。KS3,KS4L,KS4R和KR2等参数后验概率密度呈正态分布,且取值较为集中,说明这些参数对模型的水位输出结果影响较大。Simulink模型模拟产生的水位90%不确定性区间如图4(i)所示,由图可知,蒸汽发生器Simulink模型模拟结果的90%不确定区间能够完全包含(覆盖率为100%,不确定性区间宽度为0.041 m)RELAP5模型的观测数据,表明参数的假设取值范围满足要求。

图4 模型参数后验分布与不确定性区间
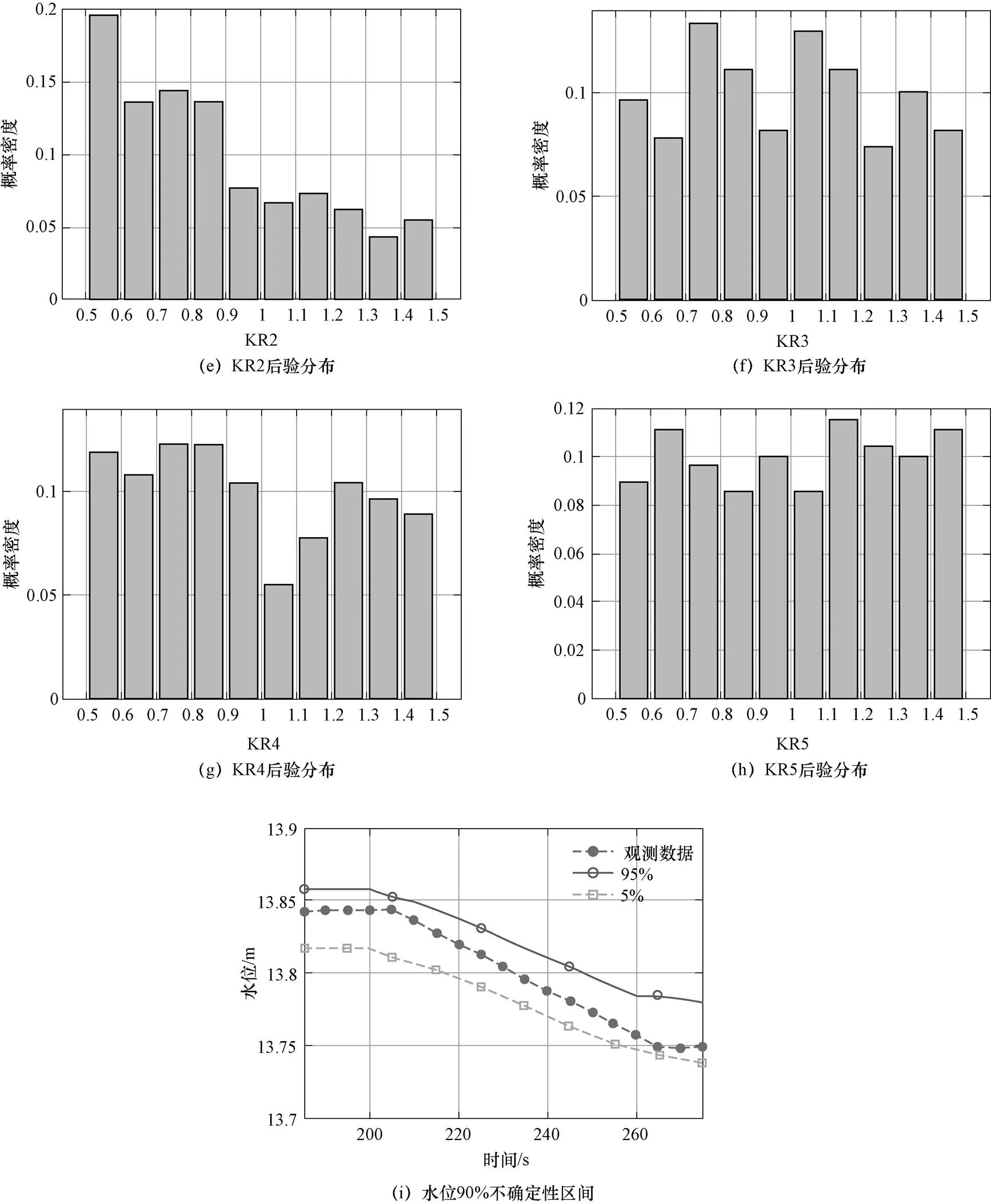
图4 模型参数后验分布与不确定性区间(续)
3 敏感性分析
3.1 目标函数
在进行敏感性分析前应根据研究模型自身特征选择目标函数,选择的目标函数应尽可能反映模型特征。选择水位确定性系数,母管蒸汽压力误差系数,出口冷却剂温度误差系数,循环流量误差系数作为目标函数,四个目标函数可根据模型输出与观测数据的偏差的大小确定参数的敏感性。敏感性分析目标函数如表2所示。

表2 敏感性分析目标函数
续表

评价目标目标函数备注 蒸汽压力 误差系数蒸汽压力相对误差 温度误差 系数出口温度相对误差 循环流量 误差系数循环流量相对误差
注:为某时刻;obs() 为观测水位;cal() 为模拟水位;obs() 为观测蒸汽压力;cal() 模拟蒸汽压力;obs() 为观测冷却剂出口温度;cal() 为模拟冷却剂出口温度;obs() 为观测循环流量;cal() 模拟循环流量。
3.2 SOBOL指数法
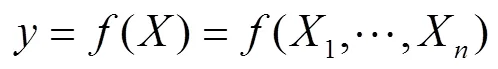
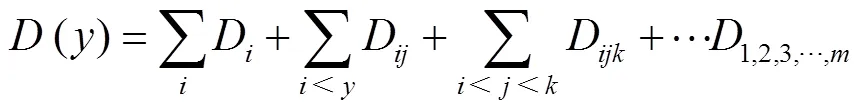
式中:D——参数产生的方差;
D——参数和参数共同作用的方差;
D——参数参数和参数共同作用产生的方差;
1,2,3,…,m——个参数共同作用产生的方差。
将式(6)归一化后可得到各参数和参数间共同作用的敏感性:

参数的各个指标:
一阶敏感度:

二阶敏感度:
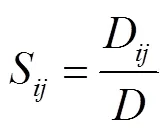
总敏感度:

式中:S——参数单独作用时的敏感度;
S——参数和参数相互作用的敏感度;
S——参数的主作用和参数与其他参数共同作用的敏感度之和;
——除了参数自身之外剩余参数的方差。
3.3 敏感性分析结果
以水位确定性系数为目标函数时,参数的一阶敏感度与总敏感度如图5(a)与图5(b)所示,由图知,敏感性参数为KS3、KS4L、KS4R和KR2,四个参数的一阶敏感度分别为0.645、0.051、0.097以及0.165,总敏感度分别为0.689、0.072、0.114和0.188。以母管蒸汽压力误差系数为目标函数时,参数的一阶敏感度与总敏感度如图5(d)与图5(e)所示,由图知,敏感性参数为KS3,KS4L和KS4R。各参数的一阶敏感度分别为0.311、0.099和0.231,总敏感度分别为0.431、0.321和0.445。以冷却剂温度误差系数为目标函数时,各参数的一阶敏感度与总敏感度如图5(g)与图5(h)所示,由图知,敏感性参数为KS3,KS4L,KS4R。各参数的一阶敏感度分别为0.425、0.163和0.285,总敏感度分别为0.424、0.233和0.354。以循环流量误差系数为目标函数时,各参数的一阶敏感度与总敏感度如图5(j)与图5(k)所示,由图知,敏感性参数为KS3和KR2,各参数的一阶敏感度分别为0.082和0.847,总敏感度分别为0.097和0.858。
由参数间的二阶敏感度分析结果可知,各模型参数在图中均有体现,表明两个参数间的相互作用对蒸汽发生器模型的仿真结果影响十分显著。
通过对四个目标函数下二阶敏感度分析以及各参数的总敏感度可知,对于关键模型输出影响明显的为子KR2,KS3,KS4L,KS4R。四个敏感参数的组合作用对关键状态量影响明显,因此在同化实验中需要对四个参数同时进行优化调整。

图5 敏感性分析结果(续)
4 同化结果验证与对比
4.1 蒸汽发生器数据同化过程
蒸汽发生器的数据同化由观测数据、蒸汽发生器模型及其模拟结果的不确定性分析和观测数据与模型的耦合方法等三个部分组成。关于观测数据与模型的耦合需要通过一个观测算子来建立联系。这个观测算子是模型参数关于可观测状态量的函数关系,应精确反映模型状态,可以是简单的线性函数或非线性模型。在蒸汽发生器模型模拟过程中,根据模型不确定分析结果,建立敏感性参数与关键状态量线性函数关系。同化的实验步骤如图6所示。
4.2 稳态验证
采用序列二次规划算法(SQP)对代价函数在敏感参数的有效范围内寻找最优解,在每次迭代过程中通过调整权重系数,来获得使代价函数最小的模型参数组合。将每次调整后的参数作为新的模型初始参数带入模型。5次同化后的模型稳态结果与稳态过程观测数据对比如图7所示。由图可知,经过5次迭代后,水位由14.055 m变为13.847 m,实际观测水位为13.843 m,相对误差由1.568%降至0.002 8%。蒸汽压力6.898 MPa升至6.955 1 MPa,实际观测压力为6.955 9 MPa,相对误差由3.19%降低至0.012%。一次侧冷却剂出口温度由289.49 ℃升至289.51 ℃,观测出口冷却剂温度为289.61 ℃,相对误差由0.041%降至0.035%。循环流量由2 817.07 kg/s升至3 198.58 kg/s,观测循环流量为3 302.494 kg/s,相对误差由15.24%降至3.42%。通过数据同化方法对模型参数进行调整,相对于同化前,水位、压力、冷却剂出口温度和循环流量同化之后的精度分别提高了99.82%、99.62%、14.63%和77.55%。由此可见,稳态时,模型输出的相对误差明显降低,同化前后的模型仿真精度提高明显。
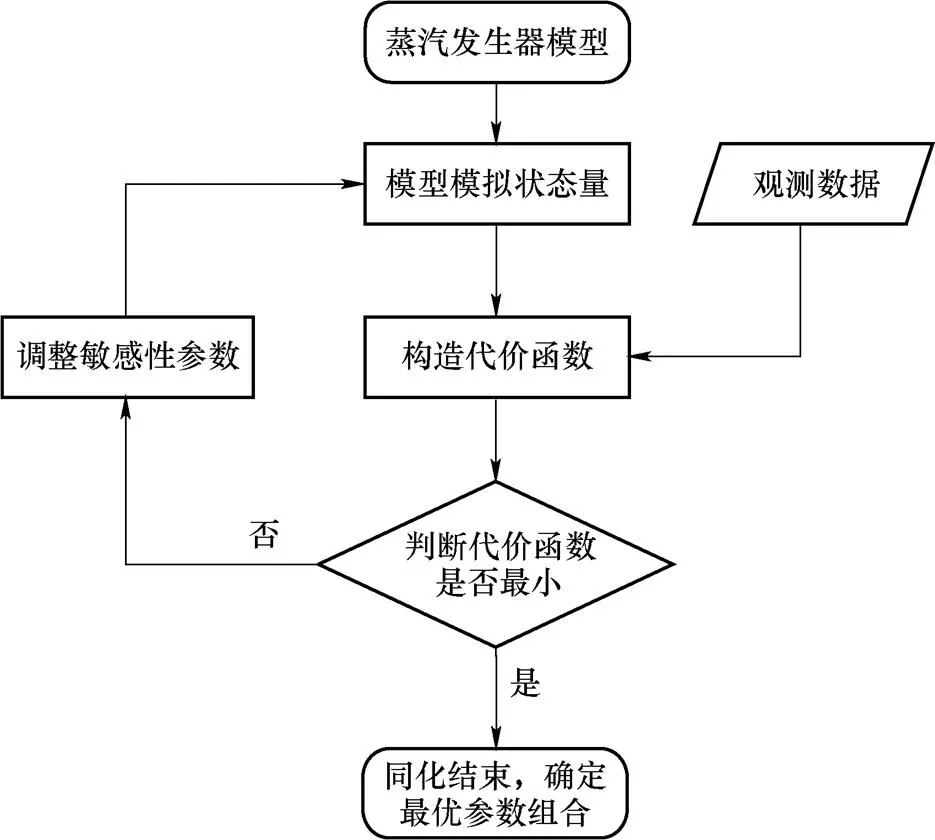
图6 同化过程流程图
4.3 瞬态验证
在瞬态工况下,重点关注蒸汽发生器水位变化,利用瞬态过程中的水位观测数据进行模型的回代检验。结合给水流量阶跃下降2%和给水温度阶跃下降2 K两种瞬态工况下RELAP5模型水位变化数据对同化后的模型进行外推检验,进一步验证方法的有效性。回代检验和外推检验的结果如图8所示。由图8可知,对同化后的模型进行模拟检验,结果表明Simulink模型模拟水位与RELAP5模型观测水位的决定系数R均在0.98以上,证明同化后的模型可以精确反映在瞬态工况时水位的变化趋势。
5 结论
本文提出了一种含有不确定性分析、敏感性分析和数据同化的蒸汽发生器模型参数优化调整的方法。该方法实现压水堆核电厂蒸汽发生器的观测数据对蒸汽发生器仿真模型的关键参数进行调整,降低模型参数的不确定度,提高模型的仿真精度。

图7 模型稳态结果对比

图8 同化模型瞬态结果对比
本文得出的主要结论如下:
(1)对于蒸汽发生器,阻力系数和换热系数是造成仿真不确定性的主要原因。
(2)该方法从模型自身出发,克服了依赖于专家经验的手工法的局限性,利用观测数据对与模型关键状态量相关的敏感参数进行同化调整。
(3)对于瞬态工况,同化后的模型能精确反映水位变化趋势,证明该方法可以大大提高模型的预测能力。
[1] 张建民. 核反应堆控制[M]. 2版. 北京:中国原子能出版社,2016
[2] 邱磊磊,张贤山,魏新宇,等. 自然循环蒸汽发生器的水位动态特性分析[J]. 核动力工程,2021,42(S2):5-9.
[3] Abdel-Khalik H,Turinsky P,Jessee M,et al. Stover T,Iqbal M.Uncertainty quantification,sensitivity analysis,and data assimilation for nuclear systems simulation[J]. Nuclear Data Sheets,2008,109(12):2785-2790.
[4] Bouriquet B,Argaud J P.Best linear unbiased estimation of the nuclear masses[J]. Annals of Nuclear Energy,2011,38(9):1863-1866.
[5] Eleveld H,Kok Y S,Twenhofel C J W.Data assimilation,sensitivity and uncertainty analyses in the Dutch nuclear emergency management system:a pilot study[J]. International Journal of Emergency Manage,2007,4(3):551-563.
[6] Bouriquet B,Argaud J P,Cugnart R.Optimal design of measurement network for neutronic activity field reconstruction by data assimilation[J]. Nuclear Instruments and Methods in Physics Research A,2012,664(1):117-126.
[7] Bouriquet B,Argaud J P,Erhard P,et al. Robustness of nuclear core activity reconstruction by data assimilation[J]. Journal of Power and Energy Systems,2012,6(2):289-301.
[8] Gong H l,Yu Y r,Li Q,Quan C y.An inverse-distance- based fitting term for 3D-Var data assimilation in nuclear core simulation[J]. Annals of Nuclear Energy,2020,141:107346.
[9] Wan C H,Huang Y H,Zheng Y Q,et al. Nuclear-data adjustment based on the continue-energy cross-section library for the fast reactor[J]. Annals of Nuclear Energy,2020.124.
[10]苏云,许以全,曹学武,等. 最佳估算程序在安全分析中的应用综述[C]. 中国核学会&中国环境学会. 全国放射性流出物和环境监测与评价研讨会论文集,2003:593-601.
[11] Beven K,Binley A.The future of distributed models:Model calibration and uncertainty prediction[J]. Hydrological Processes,1992,6(3):279-298.
[12]杨世铭,陶文铨. 传热学[M]. 4版. 北京:高等教育出版社,2006.
[13]于凯秋,孙立成,阎昌琪.“Chen”型沸腾传热计算方法用于小通道传热计算的适应性[J]核动力工程,2010,31(1):24-27.
[14]罗鹏程. 武器装备敏感性分析方法综述[J]. 计算机工程与设计,2008:29(21):5546-5549.
Research on Steam Generator Model Assimilation Method Based on 3D-VAR Algorithm
ZHANG Qi,YANG Shuhan,SUN Peiwei*,WEI Xinyu,QIU Leilei
(School of Nuclear Science and Technology,Xi’an Jiaotong University,Xi’an of Shaanxi Prov. 701149,China)
The system parameters of the steam generator change during actual operation. In order to ensure that the steam generator model can truly reflect the actual state of the steam generator, the method of assimilating the observation data of various steam generators based on the steam generator model based on the three-dimensional variational algorithm is carried out based on the observation variables such as the water level of the steam generator, the steam pressure, the primary side coolant outlet temperature and the circulating flow rate. The uncertainty analysis of the steam generator simulation model is carried out to determine the parameter adjustment range, the combination of parameters to be optimized is selected based on the analysis results of the SOBOL algorithm, the function relationship between the key parameters and the observed variables is fitted as the coupling mode between the observation data and the model, and finally the optimal parameter combination is obtained by using the optimization algorithm to solve, and the data assimilation of the steam generator model is realized. Comparing the calculated values of the model with the observational data, the results show that the simulation accuracy of the steam generator can be significantly improved, which proves the correctness of the proposed method.
Data assimilation; Steam generator model; 3D-Var algorithm; Uncertainty analysis; Sensitivity analysis
TL365
A
0258-0918(2023)05-1015-12
2022-09-09
自然科学基金面上项目(11875215)
张琪(1995—),男,陕西咸阳人,硕士研究生,现主要从事核反应堆控制与仿真方面研究
孙培伟,E-mail:sunpeiwei@xjtu.edu.cn

