基于后缘小翼的翼型反流动态失速主动控制试验研究1)

李国强 宋奎辉 易仕和 张卫国 杨永东 袁明川 吴霖鑫

* (国防科技大学空天科学学院,长沙 410073)

† (中国空气动力研究与发展中心低速空气动力研究所,四川绵阳 621000)

** (中国直升机设计研究所直升机旋翼动力学重点实验室,江西景德镇 333001)

引言

直升机在前飞过程中旋翼桨叶线速度与前飞速度的叠加会导致桨盘前行侧和后行侧桨叶的相对来流速度不对称,并且在桨盘后行侧半径小于µR|sinψ| (µ 为前进比,R为旋翼半径,ψ 为桨叶方位角)的区域会出现前飞速度超过当地线速度的现象,此时相对气流从桨叶叶素的几何后缘流向几何前缘,该区域被称为反流区.在反流区桨叶叶素工作于负迎角状态会产生负升力,使桨盘前行侧和后行侧升力不平衡,并且桨叶叶素的几何后缘会诱导严重的流动分离和反流动态失速,增加桨叶的非定常载荷,导致桨叶俯仰力矩和阻力的激增,从而增加旋翼的需用功率[1],限制前飞速度的提高.随着直升机向高速化发展[2],更高的前飞速度会促使反流区面积进一步扩大,使反流现像更加显著,因此解决反流动态失速问题,改善反流区流动分离,提升旋翼的气动效率,成为了推动高速直升机进一步发展的重要课题.

反流区的一个重要特征是反流动态失速,在对UH-60A 直升机开展的大前进比旋翼试验中发现,反流状态下也会产生动态失速现象,且反流动态失速涡的局部低压也会导致非定常气动载荷,并对变距拉杆和桨叶扭转产生很大影响[3].而国内外针对动态失速控制已开展了较多研究,例如通过翼型外形的非定常设计,实现动态失速特性的改善[4-7],通过等离子体流动控制改善流动分离[8-9],通过变前缘技术改变翼型前缘外形从而控制速度梯度对动态失速的影响[10-12],通过射流技术对局部流动进行瞬时控制[13-16],通过后缘小翼(trailing edge flap,TEF)改变翼型后缘外形从而影响动态失速等[17-19],但以上针对动态失速的研究都只在正向流条件下开展,针对反流状态下的研究仍然很少.

反流动态失速的一个重要特点是翼型的压力分布会受锐几何后缘气流分离的影响.因此为进一步研究翼型几何后缘形状对反流气动性能的影响规律,Lind 等[20]针对不同的翼型几何后缘形状开展了反流静态试验,发现反流中NACA0012 翼型的阻力比前向流中的大了2 倍,而钝几何后缘的阻力比NACA0012 翼型的小很多,因此X2TD 高速直升机的桨叶内段翼型采用了钝(椭圆)几何后缘,并且降低了弦长和安装角,袁明川等[21]在对翼型反流流场进行分析时也指出钝几何后缘对于反流流动分离具有改善效果,张威等[22]指出双钝头翼型适合作为反流区的翼型.Han 等[23]针对钝几何后缘翼型的外形开展了进一步的优化设计,优化后的翼型实现了阻力系数的进一步降低和失速性能的提升.但是钝几何后缘翼型在改善反流区性能的同时,增加了反流区外的阻力和悬停诱导功率,对悬停性能有一定影响,Giovanetti 等[24]的研究表明该优化将增加7%的悬停损耗.

反流动态失速的另一个特点是锐几何后缘气流的提前分离会导致翼型气动性能对雷诺数的变化不敏感.Lind 等[25]在使用非定常表面压力测量技术对NACA0012 翼型开展动态试验研究时发现,与经典动态失速发生在翼型静态失速迎角之后不同,反流动态失速提前开始于锐几何后缘的流动分离,从而对雷诺数的变化不敏感.Lind 等[26]发现钝几何后缘翼型的气动性能对雷诺数的变化反而很敏感,用于反流区可能会加剧气动载荷的变化,而锐几何后缘翼型因过早的流动分离反而降低了对雷诺数变化的敏感性.这为反流动态失速控制策略的提出提供了重要参考,即在利用锐几何后缘翼型对反流雷诺数变化不敏感的基础上尽量延迟反流流动分离的发生.于是Jacobellis 等[27]将NACA63-218 翼型的几何后缘向上翼面(吸力侧)偏转一定角度,并与几何后缘无偏转的翼型对比了反流中的静态气动性能,发现当几何后缘向上偏转10°时,能降低反流中50%的阻力,同时还能在一定迎角范围内降低负升力.Rice 等[28]在Jacobellis 的基础上研究了翼型几何后缘向上偏转10°时的反流动态气动性能,发现几何后缘向上偏转能降低翼型俯仰振荡过程中的俯仰力矩迟滞效应.Deanna 等[29]在Rice 的基础上通过测力和PIV 技术,进一步研究了翼型几何后缘上偏不同角度时的动态气动性能,发现上偏能显著降低升力、阻力和俯仰力矩的迟滞,并且较小的偏角有望更有效地实现反流中翼型静动态气动性能的提升.Cooper[30]以Deanna 的研究为基础,研究了后掠角对NACA63-218 翼型几何后缘向上偏转时的反流静态气动特性,发现无论有无后掠角翼型后缘的向上偏转都能大幅降低反流中的阻力.

现有的研究表明将翼型的锐几何后缘向上翼面(吸力侧)偏转一定角度,通过降低锐几何后缘与来流的夹角,能延迟反流分离的产生,显著降低反流分离导致的阻力,改善负升力和俯仰力矩,实现静动态气动特性的整体提升.因此可以假设只要几何后缘与来流的夹角维持在一定范围内,就能避免反流分离的扩大.但是反流区流动复杂,来流还受桨叶挥舞、摆振、扭转、侧风和径向流等因素的影响,采用固定几何后缘偏转角的方式只能改善有限范围内的反流分离,对复杂流动的适应性还有提升的空间.因此本文在翼型几何后缘向上偏转的基础上,尝试将固定的几何后缘替换为可动态偏转的后缘小翼,使用主动控制的方式使后缘小翼随翼型迎角的变化动态调节其偏转角,尽可能地控制锐几何后缘与来流的夹角,以实现反流动态失速的控制.并且现有的反流动态失速研究还未开展过非定常表面压力测量试验,本文基于非定常表面压力测量技术,通过翼型反流动态失速主动控制试验,重点分析了后缘小翼不同振荡参数对反流动态失速的影响规律,对比了后缘小翼动态偏转和固定偏转的差异,为研究利用后缘小翼进行反流动态失速主动控制的可行性提供了数据支撑,为改善旋翼反流区的流动分离,提升旋翼在反流中的气动性能提供了新的参考.

1 试验系统

1.1 风洞

本文试验研究基于中国空气动力研究与发展中心的FL-11 风洞开展,该风洞为低速回流式风洞,试验段尺寸为1.8 m (宽)×1.4 m (高),稳定风速范围为10～105 m/s,本研究中试验风速选择为V∞=17 m/s (基于翼型弦长c=350 mm 的雷诺数为Re=3.5×105).

1.2 翼型动态试验装置

翼型试验模型的俯仰振荡运动由基于FL-11 风洞配套研制的翼型动态试验装置[31]驱动,如图1(a)所示为该动态试验装置的安装示意图.动态试验装置通过左右立柱安装于风洞闭口试验段两侧,在左右立柱相同高度各布置有一台可同步运动的伺服电机,翼型模型横跨试验段与两台伺服电机输出轴固定,通过伺服电机的同步驱动实现翼型模型俯仰振荡运动的控制.该动态试验装置最大俯仰振荡角度幅值可达15°(角度精度0.05°),最大俯仰振荡频率达5 Hz (频率精度0.01 Hz).

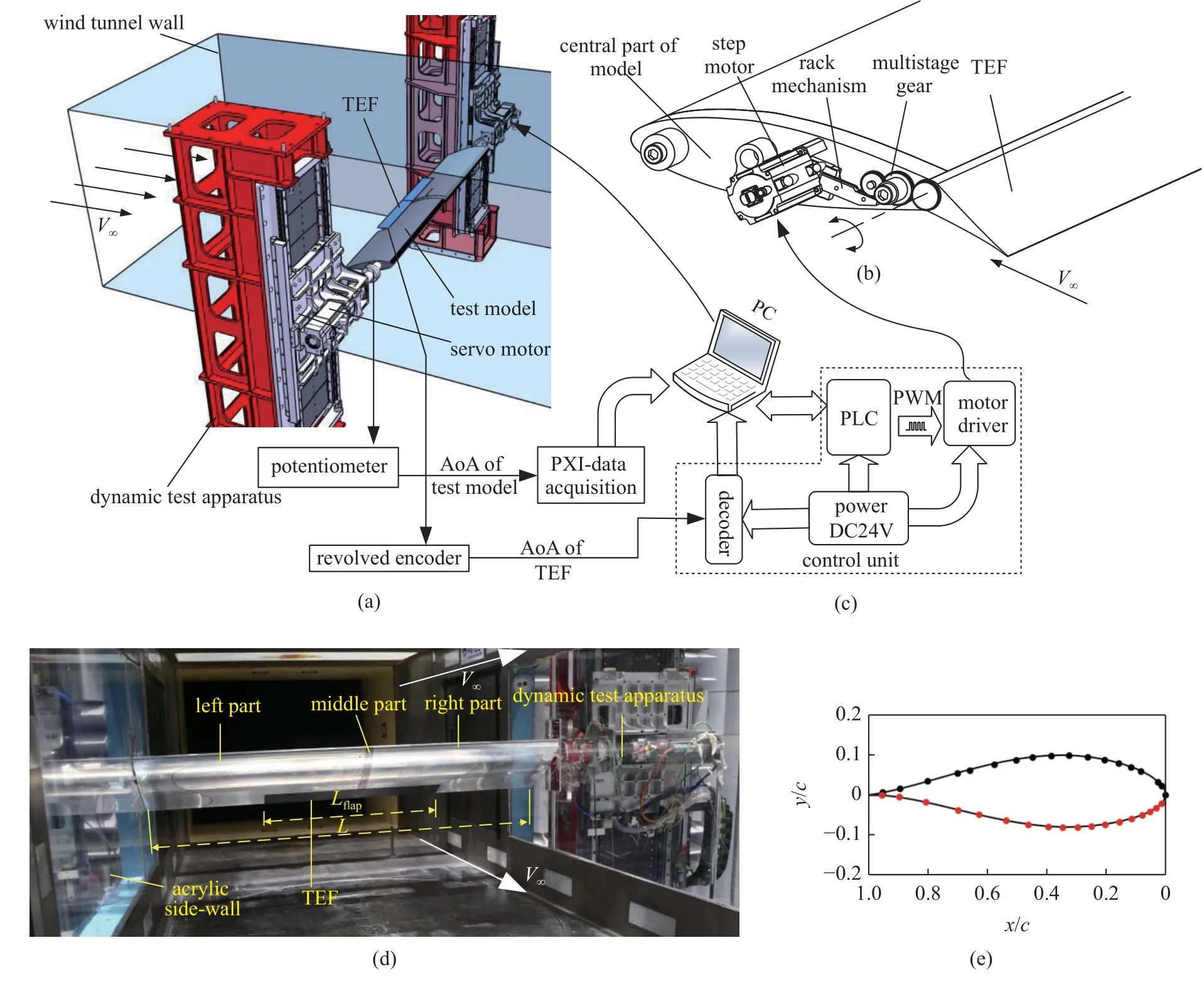
图1 (a)动态试验装置,(b)翼型试验模型剖面视图,(c)后缘小翼控制系统结构图,(d)试验段照片和(e)测压孔位置Fig.1 (a) Dynamic test apparatus;(b) Section view of airfoil test model;(c) Structure diagram of TEF control system;(d) Image of test section;(e) Location of pressure ports along airfoil

1.3 试验模型

试验模型气动外形采用XH-59A 直升机桨叶内段使用的NACA63-218 翼型[32],该翼型在反流的研究中应用较多,便于进行数据验证.图1(d)为试验模型在风洞试验段中的现场照片,模型的相关参数如表1 所示.模型关于中央件对称,分左中右3 段加工后拼接,在模型中央件上沿翼型弦向布置了36 个内径为1.6 mm 的脉动压力测压孔,测压孔的布置如图1(e)所示,上下表面各18 个,其中后缘小翼上下翼面各3 个.如图1(b)所示在模型内部布置了脉动压力传感器、电缆、步进电机和后缘小翼编码器等设备.

表1 试验模型参数Table 1 Test parameters of test model

图2 为翼型模型和后缘小翼剖面的主要尺寸图,图中分别定义了翼型模型、后缘小翼的角度和来流V∞的正方向,翼型模型和后缘小翼将分别按如下定义的运动方程运动

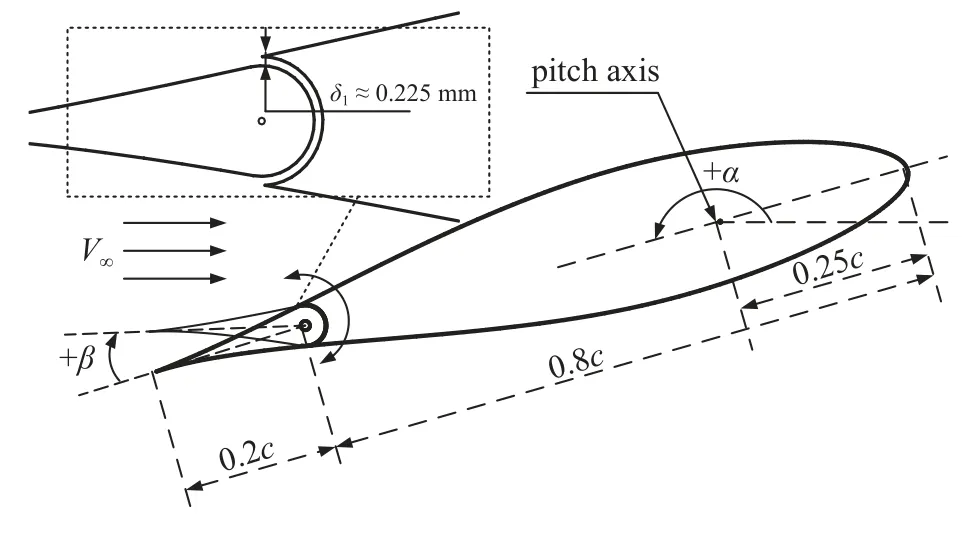
图2 试验模型剖面尺寸Fig.2 Dimensions of test model

式中 α(t) 和 β(t) 分别表示翼型模型和后缘小翼的实时迎角,抬头为正,α0和 β0分别为振荡平衡迎角,α1和β1分别为振荡幅值,f和fflap分别为振荡频率,∆ϕ 代表振荡过程中后缘小翼相对翼型模型的相位超前量.

后缘小翼采用图1(b)所示的机构进行驱动,其局部视图如图3 所示.由步进电机驱动凸轮,带动齿条机构进行周期往复运动,使后缘小翼绕平衡位置进行振荡.通过改变机构的参数及电机的转速,即可实现后缘小翼振荡幅值 β1、频率fflap和平衡迎角β0的变化.

图3 后缘小翼驱动机构Fig.3 Drive mechanism of TEF

后缘小翼的控制系统(如图1(c)所示)包含开关电源、PLC 控制器、驱动器和解码器等设备.在后缘小翼铰链转轴方向上布置有编码器,通过编码器实时反馈后缘小翼振荡的角度信号,该信号被用于控制后缘小翼与翼型模型的相位差 ∆ϕ.

1.4 测试设备

(1) 脉动压力传感器

选用ENDVECO 公司的8510B-1 系列压阻式动态压力传感器作为动态测压元件,为确保动态测压的准确性,传感器被内埋于试验模型内部,试验时压力信号随试验模型迎角信号同步实时采集.

(2) 角位移传感器

选用瑞士CONTELEC 公司的GL10010KO M340 型电位计采集试验模型的实时迎角.传感器安装于试验模型俯仰变距轴线上随模型转动,试验时角度信号除被数据采集系统实时保存外,还被用于控制后缘小翼与翼型模型的相位差 ∆ϕ.

(3) 数据采集系统

选用NI 公司的多通道数据采集卡进行试验数据的同步实时采集,采集对象为脉动压力传感器和角位移传感器的模拟信号.为方便数据的处理和分析,使试验模型在一个振荡周期T内的采样数固定为N=1024,因此采样频率fs如下

2 试验数据处理

为研究后缘小翼不同振荡参数对反流动态失速的影响规律,分别按表2 所示试验状态参数开展了试验研究,试验雷诺数Re=3.5×105,其中case1 是基准状态(baseline),此时翼型外形为标准的NACA63-218.

表2 试验状态参数Table 2 Test condition parameters

2.1 压力系数分布时间历程

通过翼型表面压力分布分析流动现象是研究流动机理的重要手段,本文将翼型上下表面压力系数随翼型迎角 α 的变化绘制成压力系数Cp和压差系数 ∆Cp分布时间历程,其中压差系数的计算公式如下式所示

式中,Cpu和Cpd分别表示上下表面压力系数,取30 个翼型振荡周期的平均值.通过压力系数随迎角的分布能定性分析翼型表面压力的整体演变规律.

2.2 压力中心xcp

压力中心是使翼型分布载荷总力矩为零的点,通过压力中心的变化能分析气动载荷对翼型俯仰力矩的影响规律,压力中心由下式定义

其中CN为法向力系数,Cm为关于1/4 弦线的俯仰力矩系数.

2.3 气动力参数

为定量分析后缘小翼对翼型气动性能的影响,除了常用的升力系数CL、阻力系数Cd和俯仰力矩系数Cm外,还引入了升力系数峰值CL,peak、阻力系数峰值Cd,peak和俯仰力矩系数峰值Cm,peak用以分析后缘小翼对反流负升力、阻力和俯仰力矩的控制效果.引入升力系数迟滞环面积CL,s和俯仰力矩系数迟滞环面积Cm,s,用以分析后缘小翼对非定常气动载荷的控制效果,该数值越大说明非定常效应越明显.

2.4 非定常数值模拟

为分析后缘小翼对反流动态失速的影响机理,采用CFD 方法建立了一套与试验模型对照的后缘小翼二维计算网格,基于运动嵌套网格技术实现翼型网格和背景网格的数据交换.图4 为网格局部视图,全局网格数量为120 万,后缘小翼网格数量为15 万,y+=1,可以看出翼型网格具有良好的正交性和贴体性.使用Fluent 对流场进行求解,边界条件为速度入口和压力出口,采用Transition SST 湍流模型,离散方法为有限体积法,压力速度耦合采用Coupled 算法,CFL数取200,对流项采用二阶迎风格式,瞬态公式采用一阶隐式.

图4 后缘小翼反流翼型二维嵌套网格Fig.4 Grid ground of airfoil with TEF in reverse flow

3 典型数据分析

为验证试验系统的可靠性,图5 给出了反流状态下静态和动态(表2,case1) 试验数据与参考文献[27]、CFD 计算结果的对比.为突出反流状态(如图2 中V∞所示,气流从几何后缘流向几何前缘)负升力的特点,后续气动力系数的正负将沿用正向流(气流从几何前缘流向几何后缘)中的定义,因此反流状态下升力系数和阻力系数将为负值.图中的动态试验数据为脉动压力传感器在30 个翼型俯仰振荡周期内的采样平均值,平均前的原始数据已绘制在图中,从图中可以看出,平均前的数据在失速前线性吻合,失速后趋势一致,平均后的数据能很好地代表动态试验中升力系数的变化规律,说明采用平均值进行分析的有效性.

图5 典型状态静动态试验数据对比Fig.5 Comparison of static and dynamic test data under typical condition

对比参考文献数据可知,本文静态试验数据在失速前与参考文献数据基本吻合,只是小迎角下升力系数较文献值稍低,失速迎角也提前了大约0.5°,分析可能由于后缘小翼驱动机构的齿轮间隙使小翼出现了微小的偏转导致,而静态与动态试验数据在失速前吻合良好,因此基本可认为试验系统可靠.图中还给出了CFD 计算结果,对比静/动态试验数据,可知静态计算数据与试验数据有一定偏差,而动态计算数据与试验数据除了失速前线性段存在一定平移外,趋势吻合良好,特别是反流动态失速发生时对非定常载荷的模拟,表明建立的数值方法能有效模拟翼型反流动态失速的非定常气动特性.

正如文中张无忌所说的，只因立场不同，就能下手如此决绝，想杀便杀，对旁人的评价丝毫不放在心上，灭绝师太和韦一笑的行事作风从本质上其实并无区别，同样“自由”。但是他们在江湖中得到的评价一个是一代宗师，一个是邪魔外道，只因二者的心性不同。

图6(a)～图6(c)给出了case1 的压力系数Cp和压差系数 ∆Cp分布时间历程,从t=-T/4 到3T/4 的过程为翼型模型从最小迎角抬头运动到最大迎角并再次回到最小迎角的一个周期,黑色虚线为运动过程中的压力中心xcp,11 条黑色竖线从左往右顺次代表典型角度压力系数分布(如图6(d)～图6(e)所示)的选择位置,x/c=1 代表翼型的几何后缘.

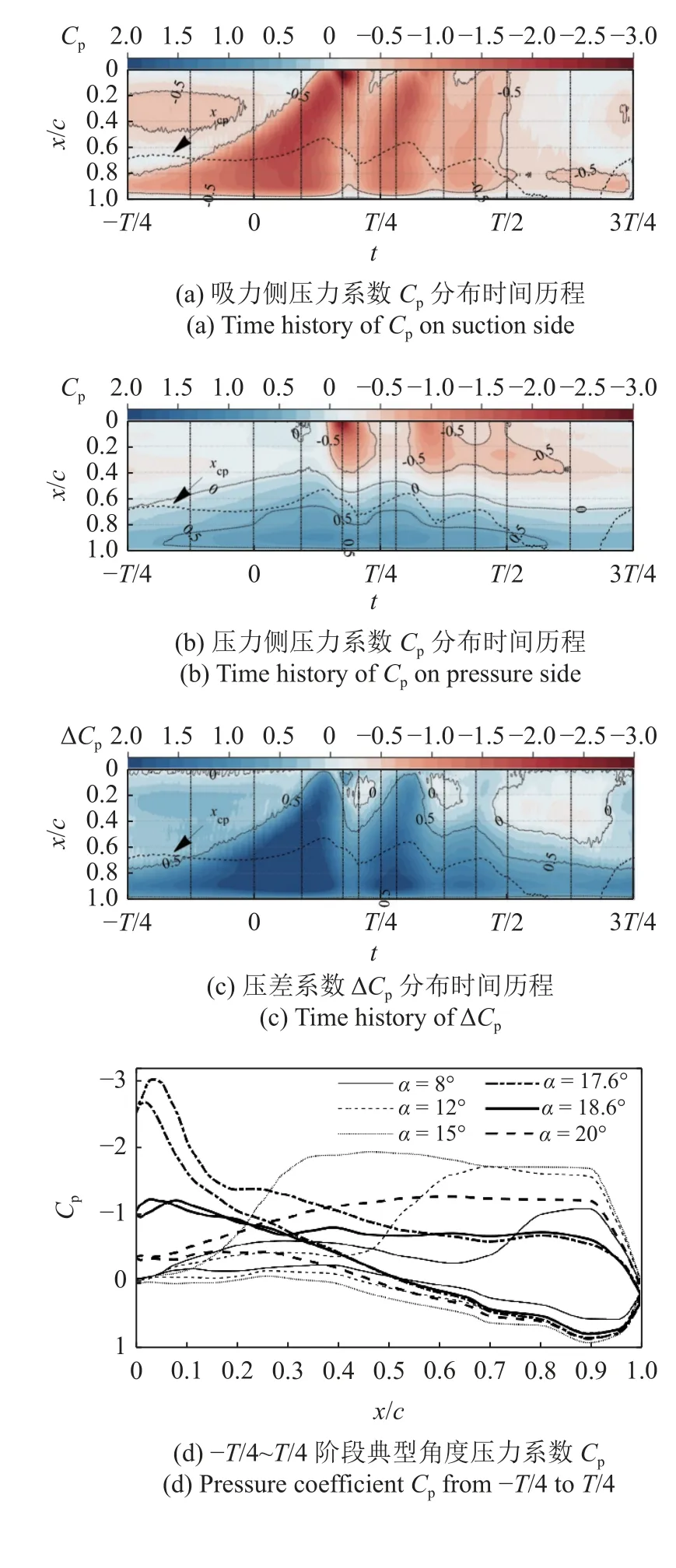
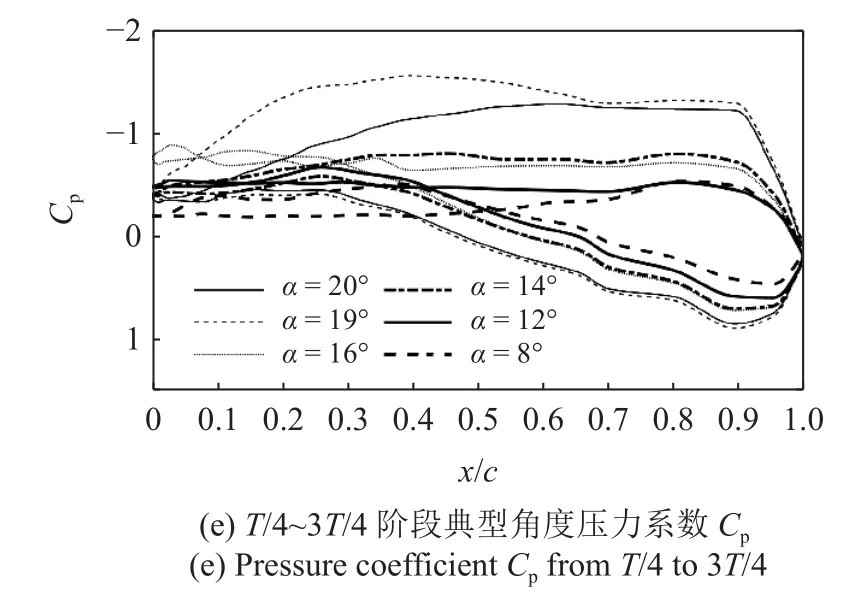
图6 基准状态压力系数、压差系数分布时间历程及典型角度下的压力系数Fig.6 Pressure coefficient,pressure differential coefficient distribution and pressure coefficient at typical angle

图7 为通过CFD 计算得到的流场,从t=-T/4到t=T/4 的过程中,吸力侧几何后缘在α=8°时出现了后缘涡(几何后缘的分离涡,TEV),后缘涡从几何后缘向几何前缘发展(图7(a)～图7(c)),分离涡带来的附加涡升力使得吸力侧低压区从几何后缘向几何前缘逐步扩大(图6(a));图6(a)～图6(b)中在α≈17.6°时吸力侧和压力侧的几何前缘又出现了一个更强的低压区,由图7(d)可知,此时在几何前缘新出现了一个前缘涡(几何前缘的分离涡,1st LEV),正是该分离涡的出现使得吸力侧和压力侧的低压特征加强,图6(d)中在α=17.6°时的压力系数分布也给出了该分离涡导致几何前缘吸力侧及压力侧同时出现局部低压的证明.

图7 基准状态典型迎角压力系数分布及流线图(↑:抬头运动,↓:低头运动)Fig.7 Pressure coefficient distribution and freestream lines of baseline (↑:pitch up,↓:pitch down)

伴随着第1 个前缘涡的脱落(1st LEV,图7(e)),吸力侧和压力侧的低压特征暂时减弱,在α≈ 20°(t=T/4)时由于吸力侧分离涡(TEV)的作用,吸力侧低压特征开始第2 轮增强,而压力侧低压特征的增强滞后了大约2°,在α=16°时再次出现几何前缘分离涡(2nd LEV,图7(h))的脱落及低压特征的减弱,在α=14°时吸力侧低压特征开始第3 轮增强,在α=12°时出现前缘涡(3rd LEV,图7(j))的脱落.在低压特征出现增强的区域,压力中心曲线xcp都出现了向几何前缘波动的现象,这主要是由于吸力侧分离涡向几何前缘移动导致,波动越大说明非定常效应越明显.

综上,NACA63-218 翼型在反流动态失速情况下,会在锐几何后缘产生后缘分离涡(TEV),分离涡随反流迎角的增加会向几何前缘移动,此外在钝几何前缘还会产生新的前缘分离涡(LEV),后缘涡和前缘涡周期性地形成、移动和脱落,在空间上会使压力中心从几何后缘向几何前缘出现周期性波动,在时间上会使压力系数出现多个极值并周期性重复,从而导致周期性的非定常效应,因此降低反流动态失速的非定常效应,可将抑制分离涡的产生、移动和降低涡的强度作为切入点.

4 试验结果分析

4.1 后缘小翼振荡相位差的影响

对于动态偏转的后缘小翼,与翼型不同的相位差 ∆ϕ 决定了不同翼型迎角下几何后缘与来流的相对偏角,研究已表明不同相位差 ∆ϕ 对翼型的气动性能有显著影响[17],因此本文首先针对后缘小翼在典型相位差 ∆ϕ=0°,90°,180°,270°下的影响规律开展了研究.图8 分别给出了表2 中case2(∆ϕ=0°),case3(∆ϕ=90°),case4(∆ ϕ=180°),case5(∆ ϕ=270°)与基准状态case1 的升力、阻力和俯仰力矩系数曲线及部分气动力参数的对比.

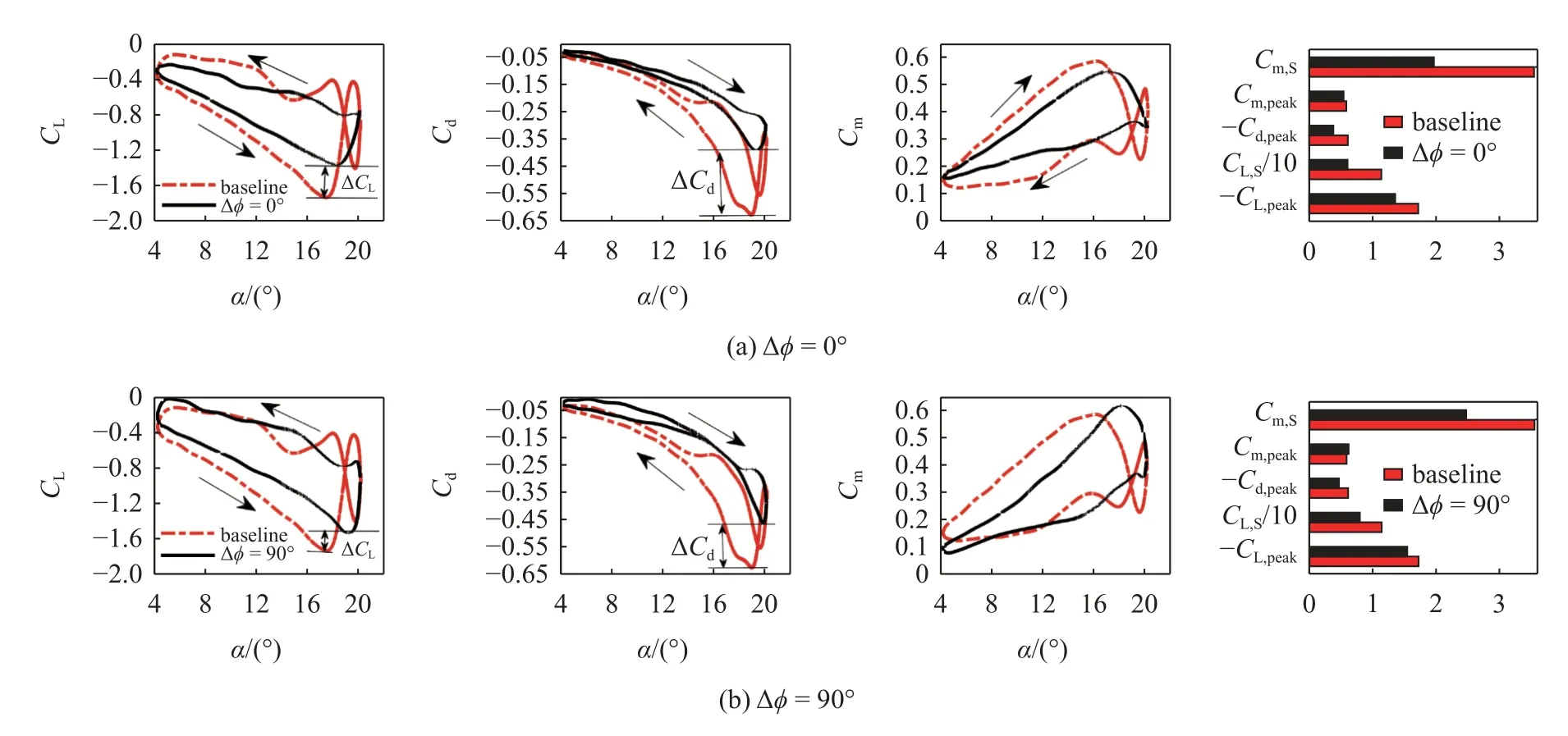
图8 典型相位差下升力、阻力和俯仰力矩系数及气动力参数对比Fig.8 Comparison of lift,drag,pitching moment coefficient and aerodynamic factors under typical oscillation phase offset

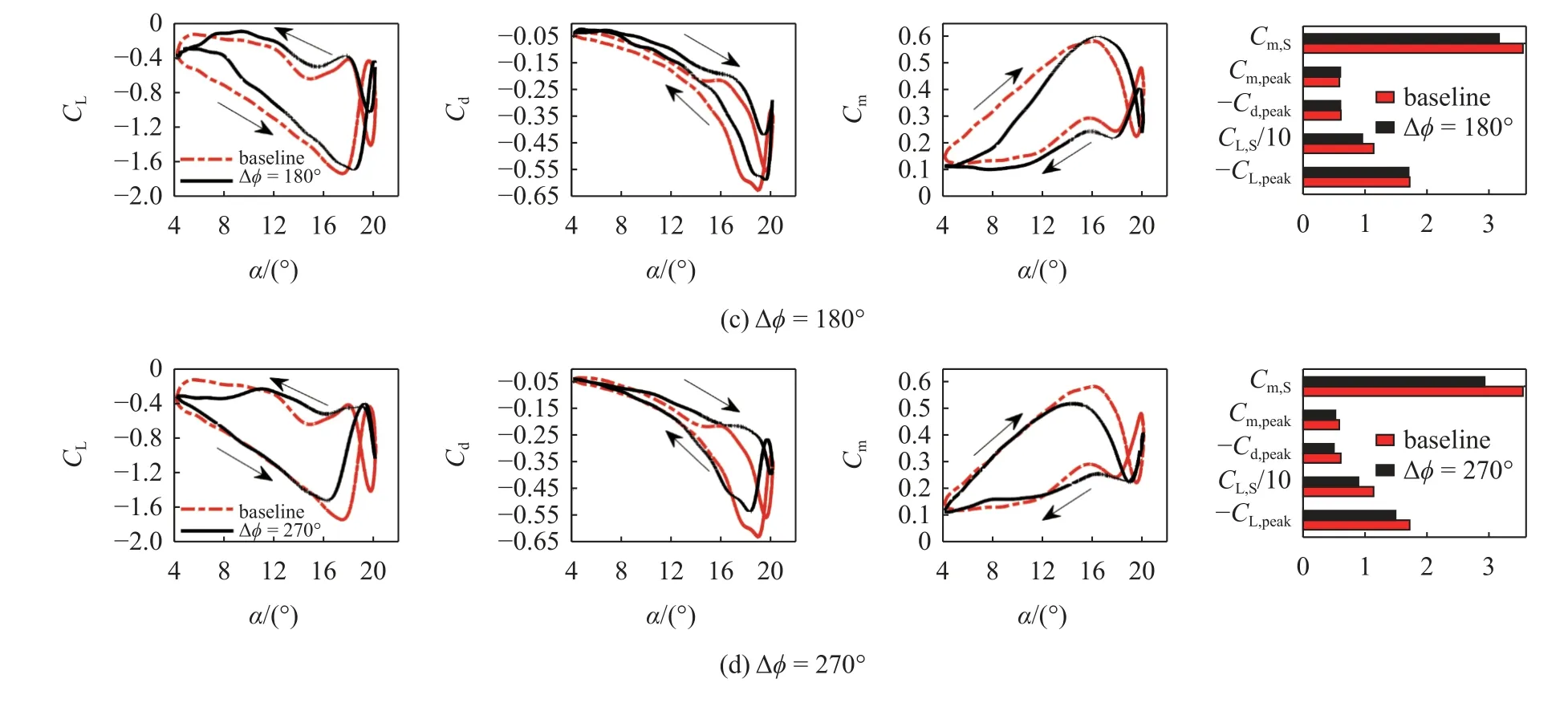
图8 典型相位差下升力、阻力和俯仰力矩系数及气动力参数对比 (续)Fig.8 Comparison of lift,drag,pitching moment coefficient and aerodynamic factors under typical oscillation phase offset (continued)

从不同相位差的气动系数曲线可以看出,相位差 ∆ϕ 对反流状态下的气动性能影响显著.其中 ∆ϕ=0°和 ∆ϕ=90°对降低翼型抬头阶段的负升力系数效果明显,虽然不能完全消除负升力,但在翼型抬头运动过程中,负升力系数的大小均低于基准状态.表3给出了各状态下的气动力参数的具体数值,从表中可知 ∆ϕ=0°和 ∆ ϕ=90°对应的最大负升力系数绝对值分别下降了21.2%(∆CL=0.364) 和10.4%(∆CL=0.179),升力系数迟滞环面积分别下降46.9%和30.3%,俯仰力矩系数迟滞环面积分别下降44.6%和30.4%,因此后缘小翼对于负升力和非定常气动载荷的控制具有一定效果.对于阻力系数的控制,同样是 ∆ϕ=0°和 ∆ ϕ=90°时的效果最明显,在翼型俯仰运动的整个周期中,阻力系数的大小整体低于基准状态,且最大阻力系数分别降低了37.5%(∆Cd=0.228)和23.8%(∆Cd=0.145),因此对于阻力系数的控制具有一定效果.

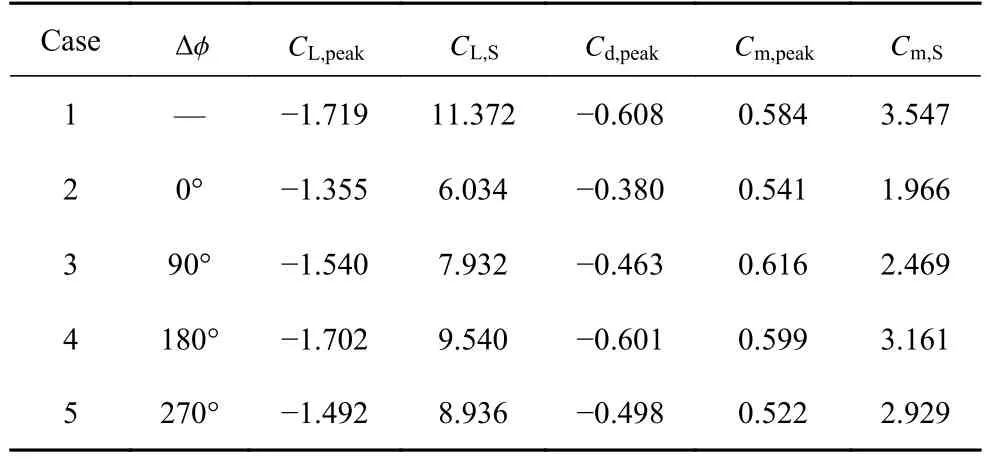
表3 典型相位差对应气动参数Table 3 Aerodynamic parameters corresponding to typical phase offset

图9 给出了 ∆ϕ=0°(case2)时吸力侧、压力侧及压差系数在一个振荡周期内的分布时间历程.由吸力侧压力系数分布时间历程可知,吸力侧低压特征较基准状态(图6(a))明显减弱,已无明显的多个涡脱落特征,且吸力侧钝几何前缘附近的气流分离也有明显改善,说明后缘小翼对于降低吸力侧分离涡强度,抑制分离涡的低压特征具有一定效果.由压力侧压力系数分布时间历程可知,压力侧几何前缘低压特征较基准状态(图6(b))明显减弱,结合吸力侧钝几何前缘的控制效果,可知后缘小翼对于抑制反流状态下钝几何前缘的流动分离具有一定效果.由压差系数分布图可知,压力中心基本维持在x/c=0.75 附近,相比基准状态(图6(c))波动更小,这也与升力系数及俯仰力矩系数曲线在失速后波动很小,且迟滞环面积下降相对应,进一步说明了后缘小翼对于降低非定常气动载荷具有积极效果.

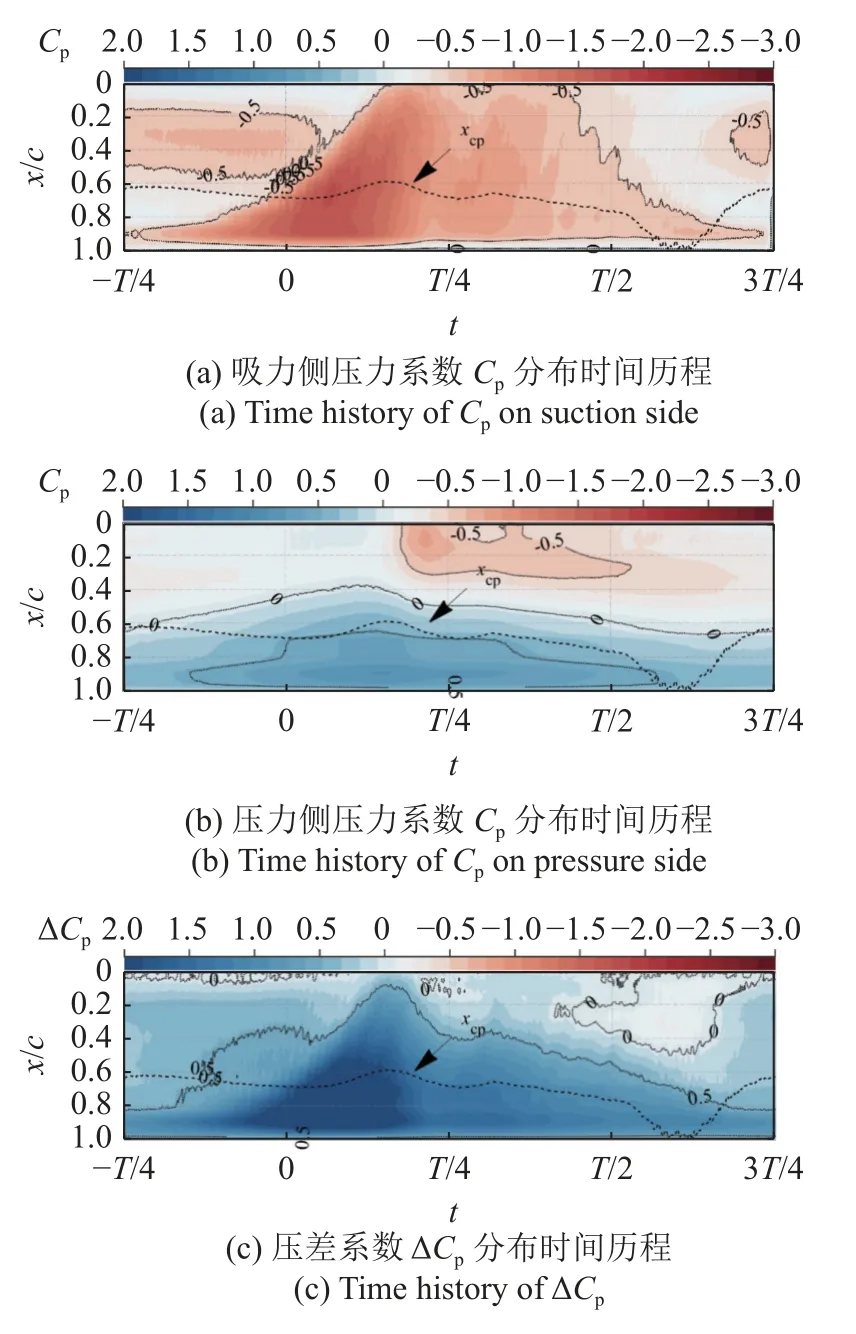
图9 ∆ϕ=0°压力系数及压差系数分布图时间历程Fig.9 Time history of pressure and pressure difference coefficient distribution when ∆ϕ=0°

4.2 后缘小翼振荡幅值的影响

前述分析表明当后缘小翼振荡相位差 ∆ϕ=0°时,同时降低翼型负升力、阻力和非定常气动载荷的控制效果最佳,因此选定 ∆ϕ=0°进一步开展后缘小翼振荡幅值 β1的研究.图10 分别给出了表2中case7(β1=0°),case6(β1=3°),case2(β1=8°)与基准状态case1 的升力、阻力、俯仰力矩系数曲线及气动力参数的对比.

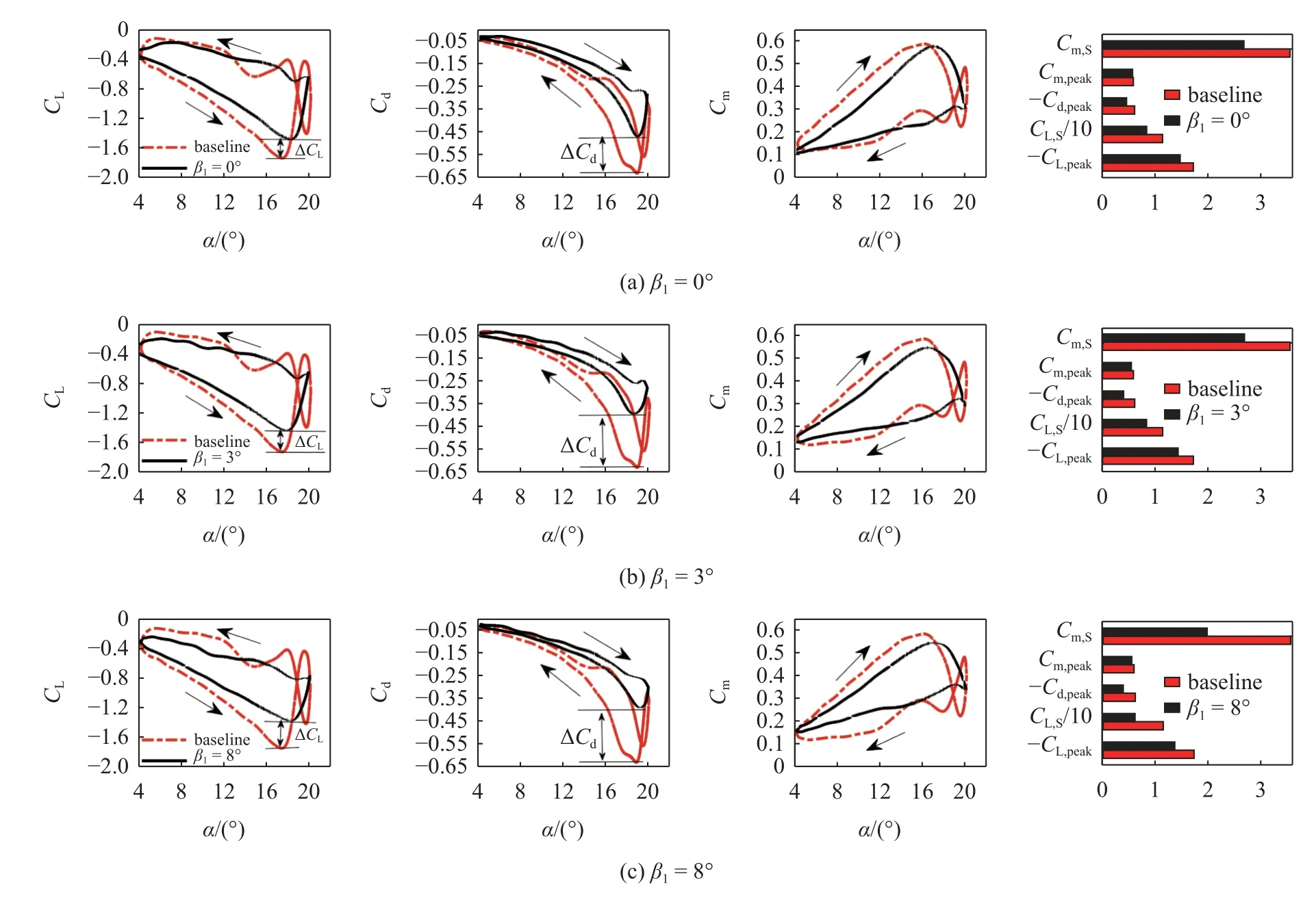
图10 典型振荡幅值下升力、阻力、俯仰力矩系数曲线及气动力参数对比Fig.10 Comparison of lift,drag,pitching moment coefficient and aerodynamic factors under typical oscillation amplitude

从不同振荡幅值的气动系数曲线可以看出,不同振荡幅值的控制效果相似,总体呈现振荡幅值越大控制效果越明显.表4 给出了各状态下的气动参数,从表中可知,随着后缘小翼振荡幅值 β1的增加,最大负升力系数绝对值在下降,当 β1=3°和8°时,分别下降了16.9%(∆CL=0.29)和21.2%(∆CL=0.364),升力系数迟滞环面积分别下降26.8%和46.9%,俯仰力矩系数迟滞环面积分别下降24.3%和44.6%,因此后缘小翼振荡幅值越大,对于负升力和非定常气动载荷的控制效果越好.对于阻力系数的控制,随着振荡幅值的增加,最大阻力系数绝对值也在下降,当 β1=3°和 β1=8°时阻力系数绝对值分别下降了34.5%(∆Cd=0.21)和37.5%(∆Cd=0.228),说明振荡幅值越大阻力控制效果越好.

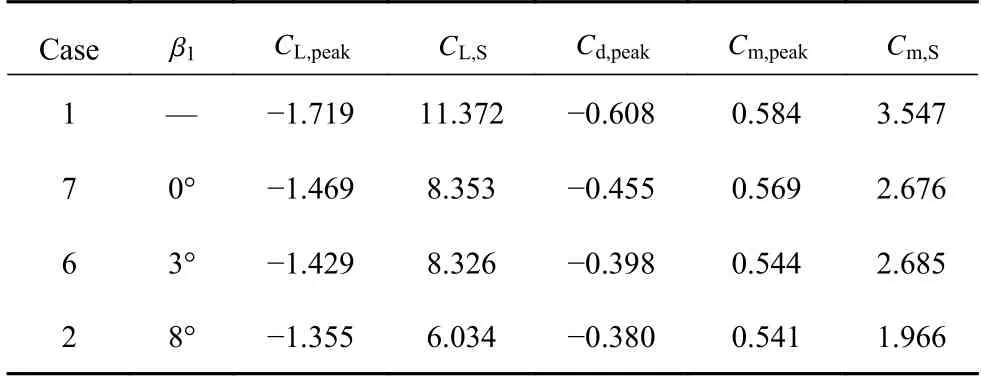
表4 典型振荡幅值 β1 对应气动参数Table 4 Aerodynamic parameters corresponding to typical oscillation amplitudeβ1

图11 给出了 β1=3°(case6)时吸/压力侧压力系数及压差系数在一个振荡周期内的分布时间历程.对比图9(β1=8°,case2)可知 β1=3°和 β1=8°对应的压力系数分布规律相似,主要差别表现在 β1=3°时压力侧几何前缘处低压区低压特征较 β1=8°时更强,该处低压特征来自于钝几何前缘的气流分离,这与 β1=8°时最大阻力系数绝对值较 β1=3°更低相对应,说明后缘小翼振荡幅值越大,对于控制几何前缘气流分离效果越好,有利于降低阻力系数.进一步对比 β1=3°和 β1=8°时翼型的气动性能可知,β1=8°较 β1=3°振幅扩大为原来的8/3 倍,负升力控制效果提升了4.3%,阻力系数控制效果提升了3.0%,因此进一步增大后缘小翼振荡幅值虽能提升控制效果,但提升能力有限.

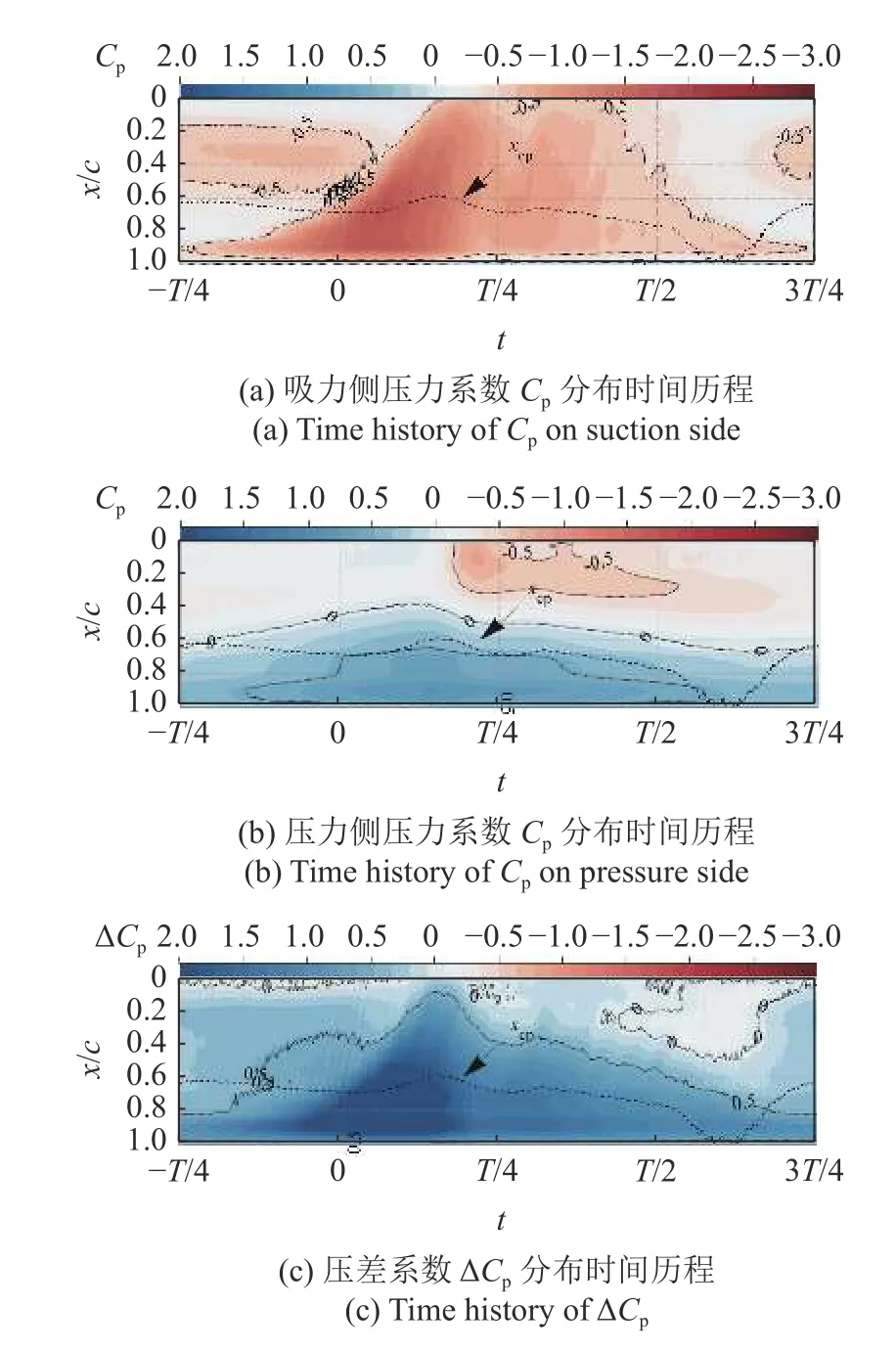
图11 β1=3°压力系数及压差系数分布图时间历程Fig.11 Time history of pressure and pressure difference coefficient distribution when β1=3°

综上,动态偏转的后缘小翼对于反流动态失速的控制效果随后缘小翼振荡幅值 β1的增加而增加,但进一步增加振荡幅值对于控制效果的提升有限.

4.3 减缩频率的影响

减缩频率k作为衡量流场非定常效应的无量纲参数,其公式为

反流区流动复杂,非定常效应明显,为进一步研究后缘小翼对非定常效应的适应能力,针对不同减缩频率开展了试验研究.图12 给出了表2 中case8(f=1 Hz,k=0.065),case9(f=1.5 Hz,k=0.097),case2(f=2 Hz,k=0.129) 和case10(f=3 Hz,k=0.194)分别与各自基准状态case11,case12,case1 和case13 升力、阻力、俯仰力矩系数曲线及气动力参数的对比.

图12 典型减缩频率下升力、阻力、俯仰力矩系数曲线及气动力参数对比Fig.12 Comparison of lift,drag,pitching moment coefficient and aerodynamic factors under typical reduced frequency

图12 典型减缩频率下升力、阻力、俯仰力矩系数曲线及气动力参数对比 (续)Fig.12 Comparison of lift,drag,pitching moment coefficient and aerodynamic factors under typical reduced frequency (continued)

从升力系数曲线可知,随着减缩频率的增加,失速迎角在不断增大,基准状态在失速后升力系数曲线都出现了不同程度的波动,而有后缘小翼进行控制时,失速后的波动有明显降低,说明后缘小翼对于降低反流动态失速的非定常载荷波动有一定效果.对于阻力系数,有控制状态的阻力系数绝对值明显低于基准状态,从表5 可知随着减缩频率的增加,最大阻力系数的控制效果分别为:20.3%(∆Cd=0.07),31.9%(∆Cd=0.152),37.5%(∆Cd=0.228)和42.6%(∆Cd=0.321),说明后缘小翼对阻力的控制效果随减缩频率增加更明显.对于非定常载荷的控制,俯仰力矩系数曲线迟滞环面积控制效果随减缩频率的增加分别为41.0%,46.0%,44.6%和40.6%,说明后缘小翼对于非定常载荷的控制在一定程度上能适应减缩频率变化.

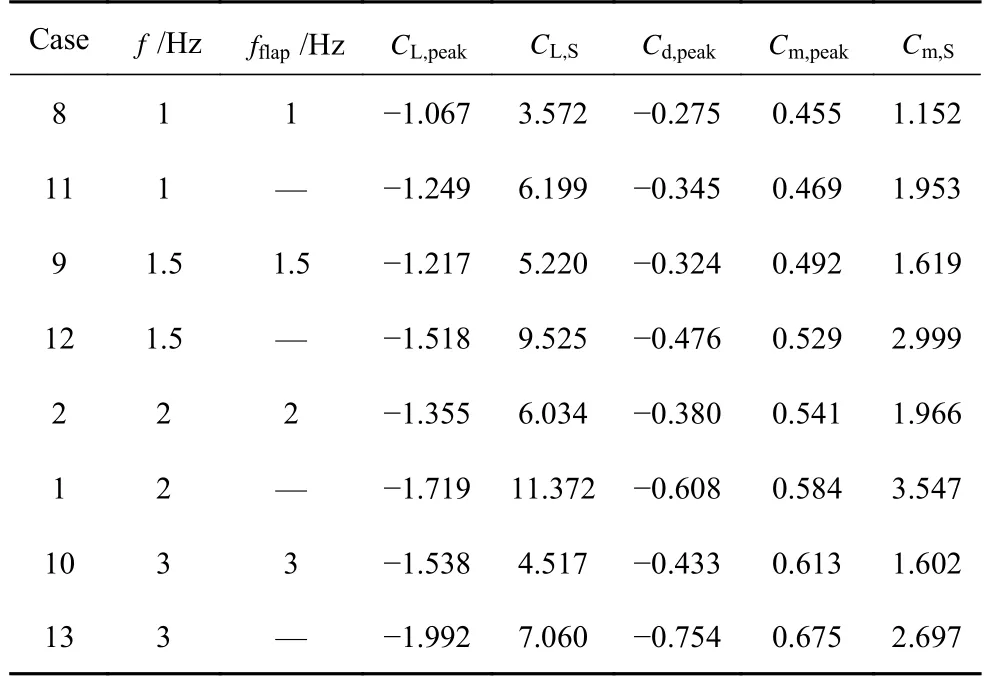
表5 不同减缩频率对应气动参数Table 5 Aerodynamic parameters corresponding to typical reduced frequency

综上,后缘小翼能降低反流动态失速中的非定常载荷波动,并能在一定程度上适应减缩频率的变化,当减缩频率增加时,后缘小翼对阻力的控制效果会更加明显.

4.4 后缘小翼动态偏转的影响

研究已表明后缘小翼向上翼面(吸力侧)固定偏转(β0=10°) 对于改善反流中的气动力效果显著[27-29],因此开展了对比试验研究,比较了固定偏转(β0=10°)和动态偏转的差异.图13 分别给出了表2中固定偏转(fixed) case14,case15,case16,case17,动态偏转(dynamic) case8,case9,case2,case10 及基准状态(baseline) case11,case12,case1,case13 的升力、阻力和俯仰力矩系数曲线对比.从图13 可以看出,动态偏转和固定偏转对于反流状态下的负升力、阻力及俯仰力矩都有一定的改善.

图13 动态偏转和固定偏转升力、阻力、俯仰力矩系数曲线对比Fig.13 Comparison of lift,drag and pitching moment coefficient between dynamic pitching and fixed deflection

结合表6 的气动参数可定量分析动态偏转与固定偏转的差异,对于升力系数的影响,动态偏条件下除了最大负升力系数绝对值比固定偏转稍小外,升力系数曲线的迟滞环面积也始终比固定偏转小,这是动态偏转对不同翼型迎角适应性优于固定偏转的一个体现;对于阻力系数,动态偏转和固定偏转的控制效果相似,但动态偏转在最大阻力系数的控制效果上均优于固定偏转;对于俯仰力矩系数,动态偏转与固定偏转都能明显降低迟滞环面积,而动态偏转迟滞环面积较固定偏转更小,因此对于非定常载荷的控制效果更优.

上述分析说明,动态偏转与固定偏转都能有效改善翼型在反流中的动态气动性能,且动态偏转对于不同翼型迎角的适应能力优于固定偏转,因此能取得更好的非定常载荷控制以及更好的阻力和负升力改善效果.

5 结论

本文基于带后缘小翼的翼型试验模型,针对反流动态失速导致的负升力、阻力和非定常载荷增加问题,研究了后缘小翼动态偏转条件下不同振荡参数对翼型气动性能的影响规律,分析了不同振荡参数对反流动态失速的控制效果,得出以下结论:

(1) 当相位差 ∆ϕ=0°时,动态偏转的后缘小翼能改善反流动态失速过程中钝几何前缘的流动分离,且能同时实现负升力、阻力和俯仰力矩的控制;

(2) 动态偏转的后缘小翼对于反流动态失速的控制效果随后缘小翼振荡幅值 β1的增加而增加,但进一步增加振荡幅值对于控制效果的提升有限;

(3) 动态偏转的后缘小翼能在一定程度上适应减缩频率的变化,当减缩频率增加时,后缘小翼对阻力的控制效果会更加明显;

(4) 后缘小翼的动态偏转与固定偏转都能改善翼型在反流中的动态气动性能,而动态偏转对于不同翼型迎角的适应能力优于固定偏转,因此能取得更好的非定常载荷控制以及更好的阻力和负升力改善效果.