基于不同路堤加筋形式的土拱效应离散元

曹军, 叶庭, 李潭潭, 王康宇

(1.中国建筑第八工程局有限公司, 上海 200120; 2. 浙江工业大学土木工程学院, 杭州 310014)

桩承式路堤能有效减小路堤沉降、提高地基稳定性,是软土地基上快速填筑路堤较为安全、经济、可靠的方式[1]。土拱效应是桩承式路堤荷载传递的主要机理之一,为了防止土拱效应的退化,一般会在路堤中铺设加筋层,这是利用了加筋体的拉膜效应。在这种桩网结构的路堤中,既有拉膜效应又存在土拱效应,两者相互影响、共同发挥作用。

英国规范 BS8006[2-3]通过临界高度来判断路堤荷载是由加筋体承担还是土拱效应和拉膜效应分别承担一部分。Burke等[4]以土工布作为加筋体开展了二维活动门离心模型试验,试验过程中采用粒子图像测速法(particle image velocimetry,PIV)技术对路堤内的土体变形机制和加筋体变形进行观察。研究结果表明:加筋体上的竖向应力呈均匀分布,造成的加筋体的变形呈抛物线形状是合理、保守和符合实际的;路堤表面沉降轮廓更符合高斯分布而不是抛物线形分布;在加筋体上方出现了一个抛物线膨胀区,沉降带的形状是一个竖直线和漏斗线的组合。陈强等[5]开展室内模型试验对土拱的形态和演变规律进行了试验研究,试验表明:砂性土中土拱不是恒定不变的; 而是处于不断变化的状态;砂性土中的土拱形态由下而上从抛物线转变为椭圆曲线。郝臣儒等[6]运用FLAC3D软件进行数值模拟研究土工格栅在黄土地区对在役路堤蠕变变形机制的影响,研究表明填筑过程中,土拱效应远大于张拉膜效应,但随着工后蠕变,张拉膜效应发挥的作用逐渐增大。芮瑞等[7]通过一套阵列式多活动门试验装置,采用尼龙和格栅两种材料作为加筋体研究了土拱效应和拉膜效应的耦合效应,试验结果表明:当路堤高度较低时,采用拉伸模量较高的加筋体能够提高桩的荷载分担比。杨广庆等[8]依托现场试验,在垫层上铺设双向土工格栅形成桩网复合基础,研究了桩间距和垫层形式对高速公路桩承式加筋路堤力学行为的影响,研究结果表明:路堤临界高度为1.0～1.5倍桩净间距;桩承式路堤的荷载转移以土拱效应为主,拉膜效应为辅。李格烨等[9]采用铝棒相似土进行了平面应变Trapdoor模型试验,研究了局部静载作用下加筋对土拱效应的影响,结果表明:在自重和局部静荷载作用下,筋材的使用明显地减少了土拱的退化;与无筋情况不同,筋材的存在使得土拱在卸载阶段仍继续退化。

然而,上述研究都是在单一加筋形式下对土拱效应的研究,没有考虑不同加筋形式对土拱效应的影响。进一步的,受限于试验的观察视角和数据的获取困难,上述研究都无法对加筋条件下的路堤内应力重分布现象进行分析,对土拱效应和拉膜效应的共同工作机制还缺乏进一步的研究。因此,现基于Xu等[10-11]开展的室内Trapdoor模型试验,采用离散元软件MatDEM[12],建立二维活动门试验的数值模型,并通过将双向土工格栅二维化的方式,探究了不同加筋形式对土拱效应的影响。

1 室内模型试验概述

Xu等[10-11]用圆柱形铝棒相似土作为路堤填料进行了二维Trapdoor试验,室内模型试验装置如图1所示。路堤底部均匀铺有5层直径为5 mm的铝棒垫层,垫层以上土体由直径为3、4、5 mm,长度为50 mm的铝棒按质量比1∶1∶1混合以20 mm为一层进行填筑。铝棒相似土的内摩擦角φ为21°,填料重度为22.4 kN/m3。垫层下有7个宽度B= 128 mm的硬木块(B1～B7)。填料自重作用下的Trapdoor 试验过程为:刚开始时,活动门(B4)每次下移Δs约0.2 mm,直至位移达到2 mm,而后每次下移约1.2 mm直至总位移达到30 mm,详细信息见文献[10-11]。选取其中的填料自重作用下的Trapdoor试验作为数值模拟的对象。

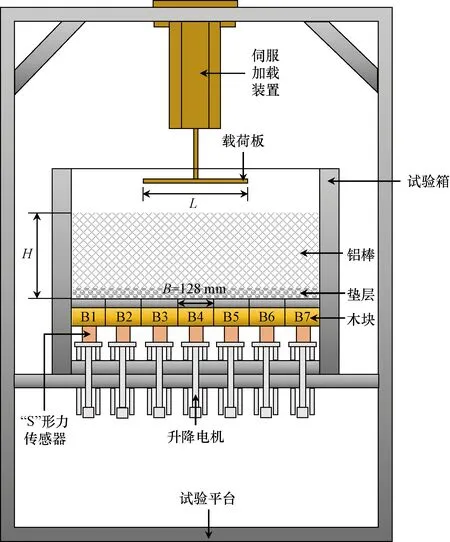
B为硬木块的宽度;H为填筑高度;L为加载板宽度图1 试验装置图[10]Fig.1 Schematic of test apparatus[10]

2 离散元模型的建立

2.1 细观参数的确定

目前MatDEM可以实现二维和三维离散元建模,其二维的实现是将球颗粒的运动限制在一个平面内,而铝棒的断面是圆形,因此二维离散元模型中单元的质量定义为

m=ρπR2×1

(1)

式(1)中:ρ为铝棒密度;R为单元半径。

由于圆柱形铝棒的力学性质比较简单,采用测量休止角的方式进行细观参数的标定[13],采用线性接触模型。得到的填料微观参数如表1所示。关于加筋材料,采用Gu等[14]的双向土工格栅作为加筋体模拟对象。为实现对土颗粒穿过格栅孔现象的模拟,提出将双向土工格栅二维化的方法,如图2(a)所示,通过消除填料颗粒和肋条颗粒之间的作用力,使上部土体颗粒穿过肋条区域,而节点颗粒之间通过肋条颗粒相连接传递拉力。在DEM模型中,用clump来模拟加筋体,双向土工格栅中,节点颗粒半径5 mm,肋条颗粒半径2.5 mm,相邻肋条在两个方向上的间距为40 mm;土工布的生成方法则是将节点颗粒替换成肋条颗粒,如图2(b)所示。通过模拟拉拔试验[14]确定了加筋体的细观参数(表1),相应的拉伸曲线如图3所示。可知DEM模拟结果与试验结果斜率基本一致,说明DEM模型可以正确反映实际双向土工格栅的拉伸性能。

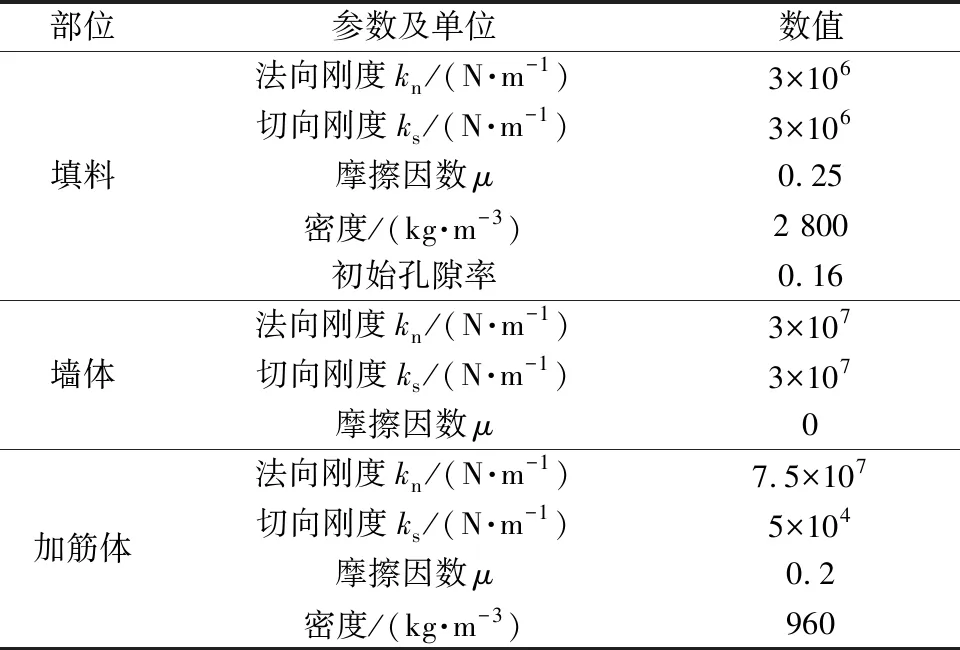
表1 细观参数表Table 1 Micro-mechanical parameters

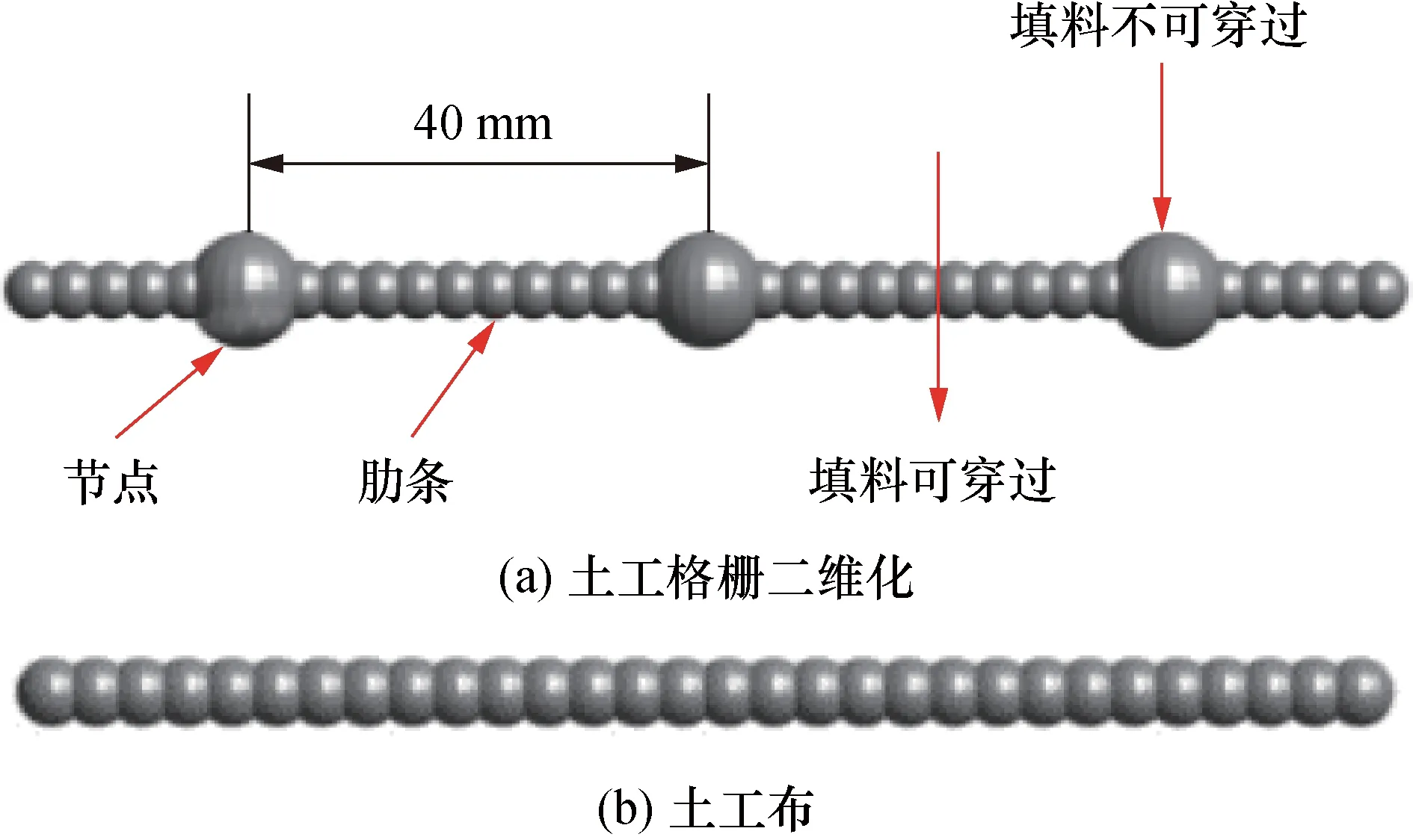
图2 加筋体DEM模型Fig.2 DEM model of geosynthetic reinforcement

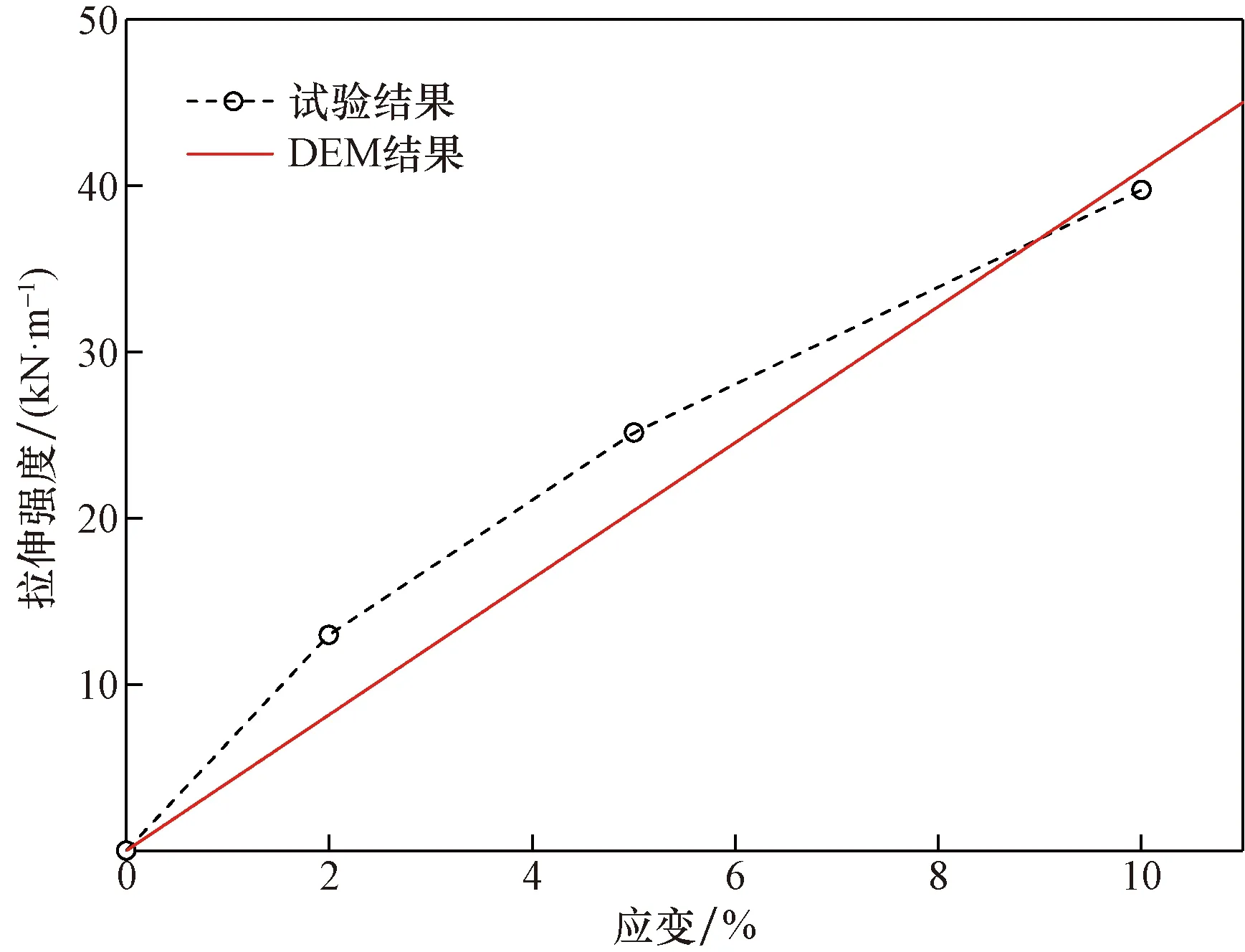
图3 拉伸曲线Fig.3 Tensile test curves

2.2 活动门离散元模型

基于Trapdoor室内模型试验,建立了如图4所示的Trapdoor的数值模型,其中,用固定单元组成的墙体来模拟试验箱和垫层底部的木块,活动单元来模拟铝棒,初始试样的制备则是采用Wang等[15]中的分层制样法,由于MatDEM中的墙体是有厚度的,所以提出一种构造无厚度墙体的方法:层与层之间有一道由两道墙组成的隔墙,属于同一层的墙和活动单元之间无作用力,如图5所示。通过移动中间底墙来模拟活动门的下移,下移过程和试验过程一样,初始时,Trapdoor每次下移约0.2 mm,直至位移达到2 mm,而后每次下移约1.2 mm直至总位移量达到30 mm,模拟过程不考虑试验箱和底部木块的摩擦。填料底部有5层直径为5 mm的ball规则排列模拟垫层。含加筋时,加筋体的两端颗粒固定移动方向,只能上下移动。3组数值模拟方案如表2所示。

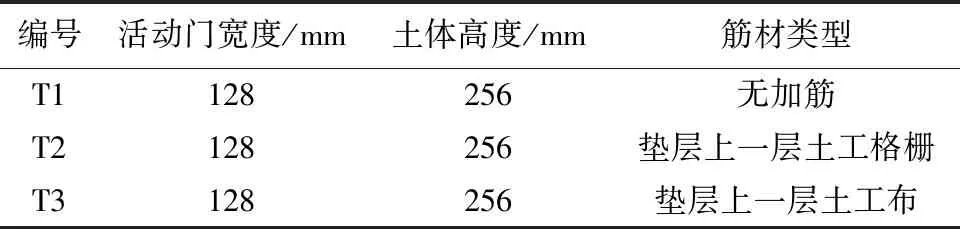
表2 数值模拟方案Table 2 Numerical simulation details

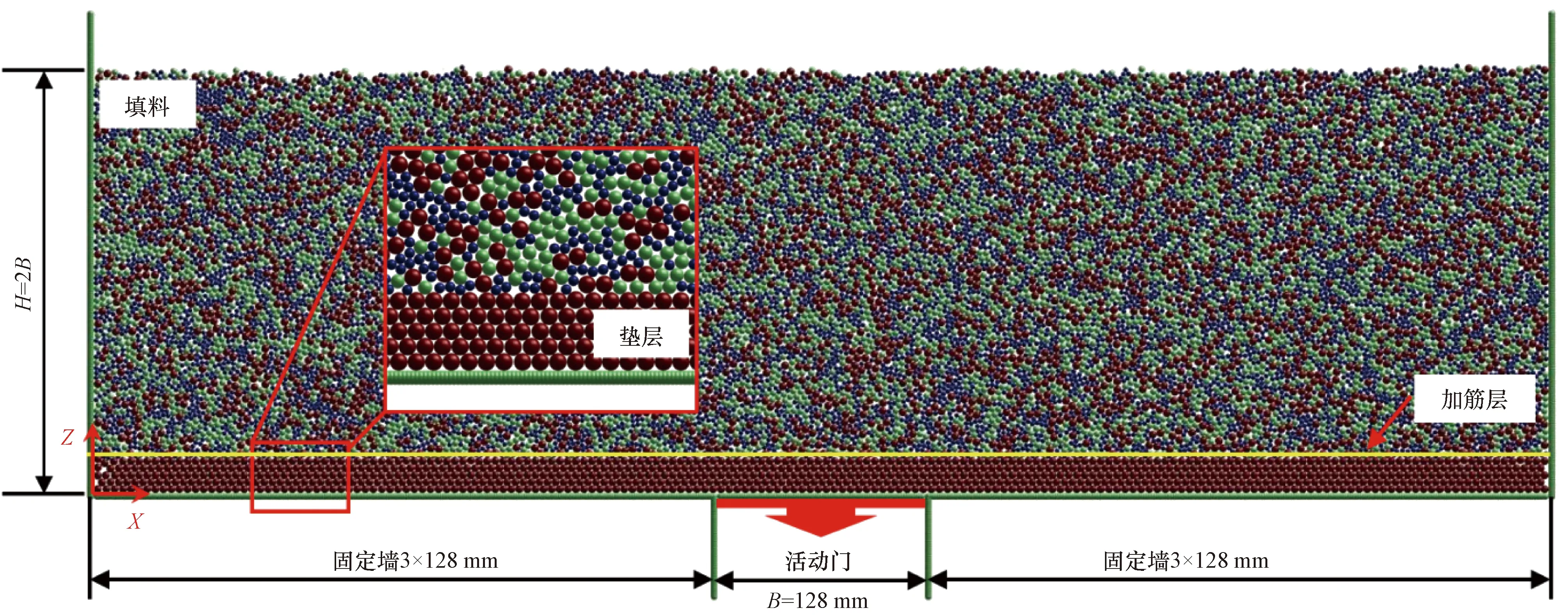
图4 Trapdoor离散元模型Fig.4 Trapdoor DEM numerical model

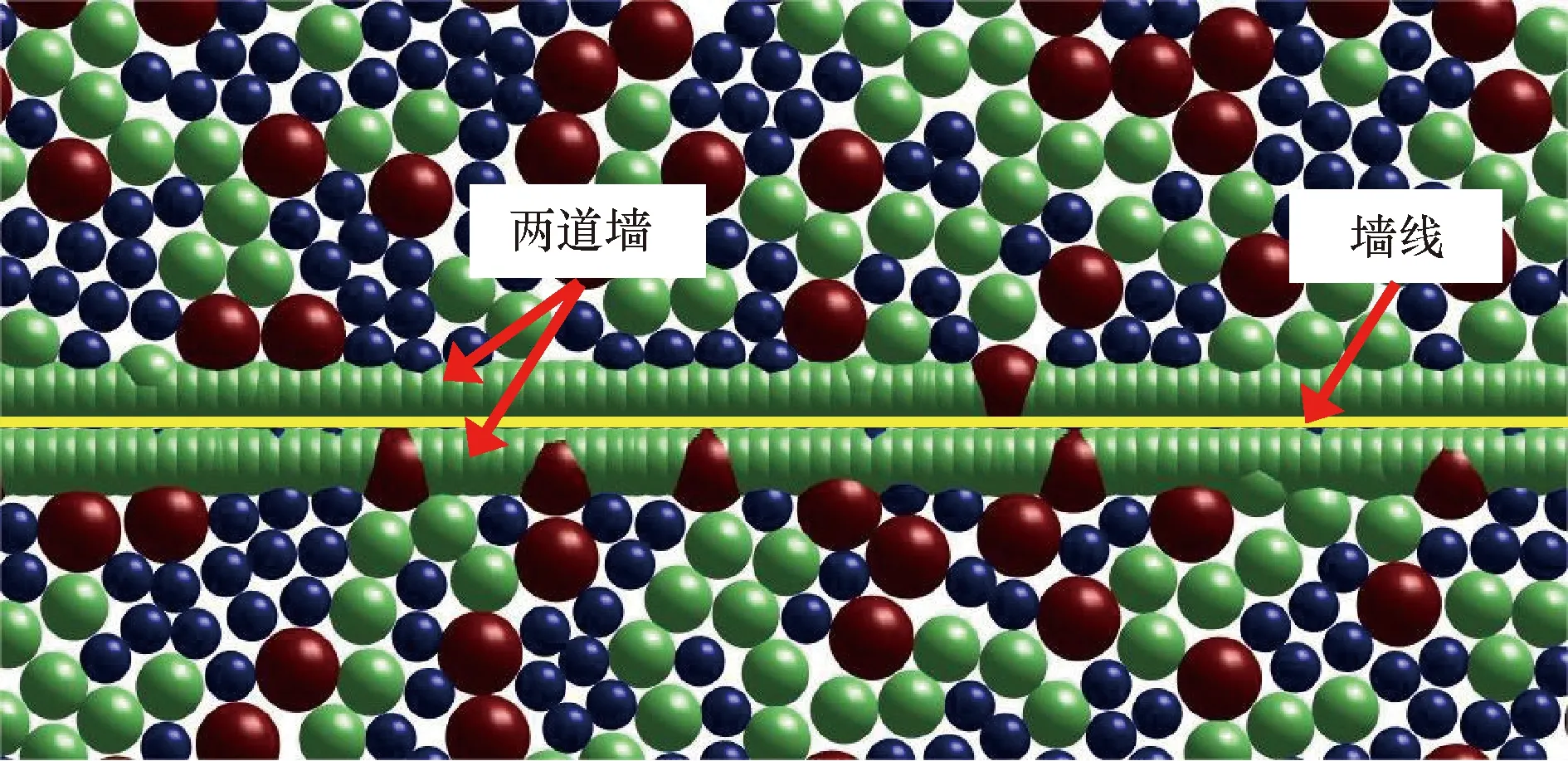
图5 隔墙示意图Fig.5 Diagram of the partition wall

2.3 数值模拟结果验证

McNulty[16]定义了土拱率来描述土拱效应的强弱,其表达式为

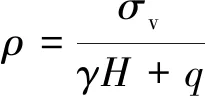
(2)

式(2)中:σv为作用在Trapdoor上的平均竖向应力;γ为土的重度;H为土体厚度;q为作用在土体表面的均布荷载,不考虑加载作用,在数值模拟中,q用初始状态活动门上平均竖向应力代替,土拱率越小表明土拱效应越强。

对自重荷载作用下Trapdoor试验进行DEM模拟结果验证,如图6所示为土体高度为2B的土拱率随活动门归一化位移δ(δ=Δs/B)的变化关系对比图。可以看出,土拱率的变化均分为初始拱、恢复阶段和极限状态3个阶段。在初始拱和恢复阶段两者数值基本吻合,从归一化位移δ=7.19%开始,数值土拱率曲线产生了较大波动,这是由于此时在活动门边界处土体中形成了复杂的剪切带,颗粒运动的离散性和尺寸效应会对土体中的传力结构产生重要影响,但总体来说DEM结果与模型试验结果变化规律基本一致,说明以上建模过程和细观参数的选取可以真实反映实际模型试验。

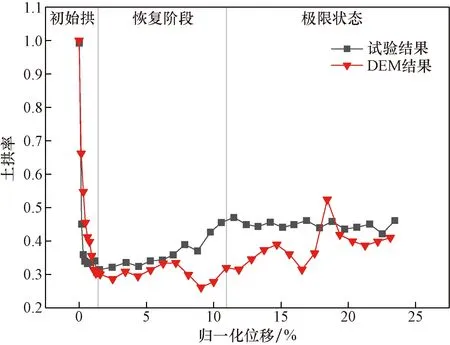
图6 DEM和试验土拱率曲线Fig.6 Curves of soil arching ratios from DEM results and laboratory test results

3 结果分析

3.1 土拱率分析

通过图7所示3组试验方案的土拱率随归一化位移的变化可以发现,在初始拱阶段Δs<2 mm时,3种方案的土拱率快速减少,速率基本一致,之后无加筋情况土拱率进入恢复阶段,变化趋缓。对于土工格栅加筋情况,在δ=4.38%,土拱率为0.18后进入一段平缓发展期,此时土体内受力结构保持稳定,待活动门位移达到A点后,土拱率在δ=14.69%(B点)和δ=19.38%(D点)时急剧增加,此时土体内的土拱结构发生了改变,

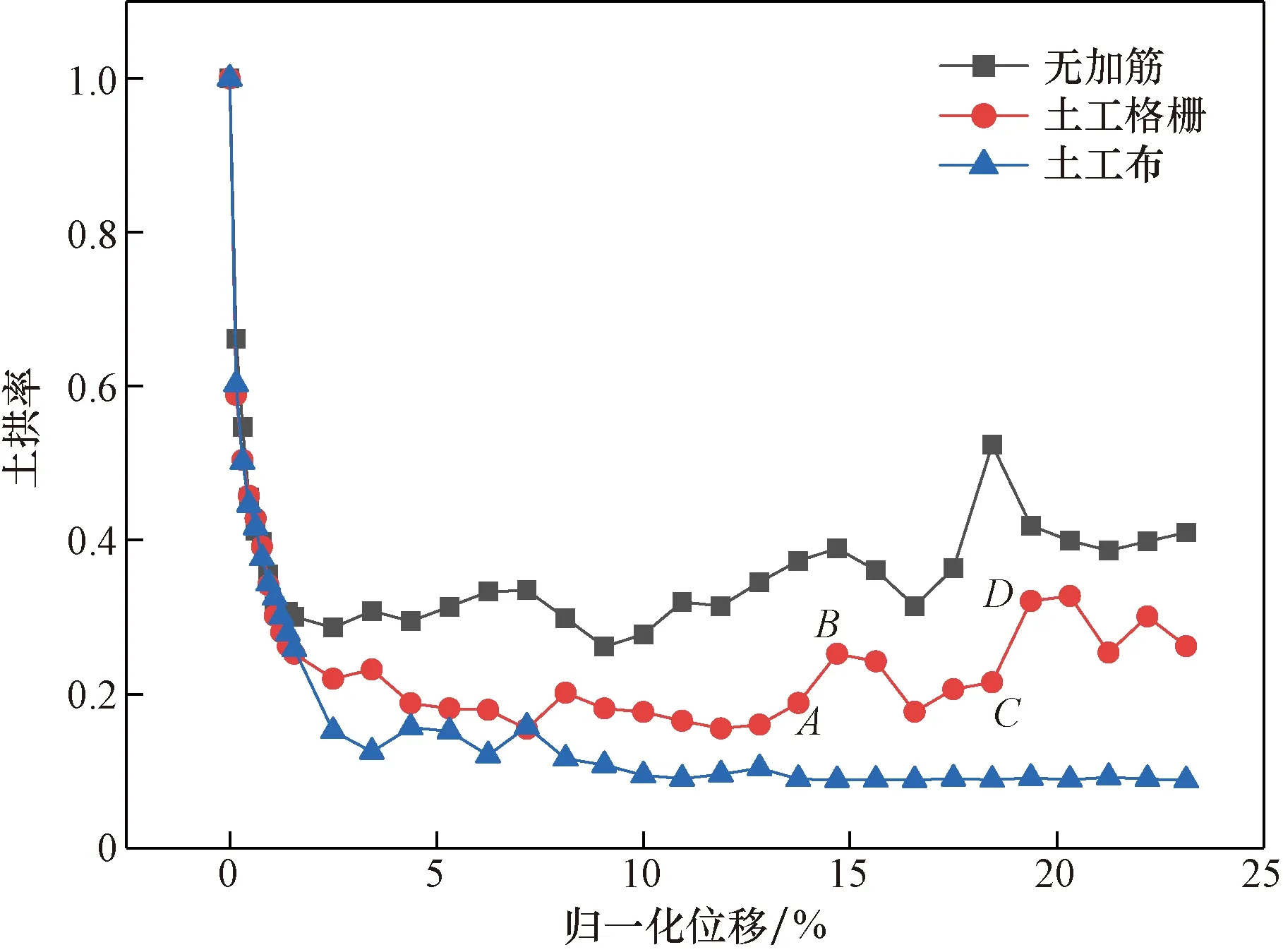
图7 土拱率变化曲线Fig.7 Curves of soil arching ratios from DEM

如图8所示,此时各点活动门附件处的土体颗粒位置情况,可以看出,在加筋体节点下形成了空隙,随着活动门的下移,在活动门边界处土体颗粒发生了垮塌,土工格栅加筋方式下拱脚处为受力的薄弱点。对于土工布加筋情况,从δ=8.13%开始土拱率基本保持在0.1,此时土工布和下部的垫层颗粒完全脱离,土体内颗粒不再受活动门下移的影响。

总体来看,在Δs=2 mm后,含加筋情况下的土拱率一直比无加筋情况小,说明加筋可以有效提升土体内的荷载转移效率,而在加筋情况中,在A点前两者土拱率相差不大,后来土工格栅加筋情况下发生了土体垮塌现象导致土拱率的退化,土工布加筋情况下则保持稳定,表明土工布比土工格栅更能保持土体内部土拱结构的稳定。

3.2 位移分析

路堤填料的相对滑动是土拱效应发生的根本原因,路堤填料位移分布规律在一定程度上能够反映“土拱结构”的形态[17]。通过MatDEM中的d.data中记录的活动单元位移数据,以活动门下移值Δs为基值,将颗粒沉降值划分为8等份,并采用8种不同的颜色对颗粒进行分组标示,以此绘制土体沉降位移云图。如图9所示为Δs=29.6 mm时土体填料沉降位移云图。可以看出,加筋体的存在减少了加筋层以上土体颗粒的差异沉降,阻止了竖向滑移面的上移,使土拱效应没有过快产生退化,保证了土拱效应的发挥和稳定;对于加筋体为土工格栅时,节点以上土体颗粒受到阻碍下沉速度慢于土工格栅室上颗粒(即肋条以上土体),差异沉降的产生将形成拱结构。

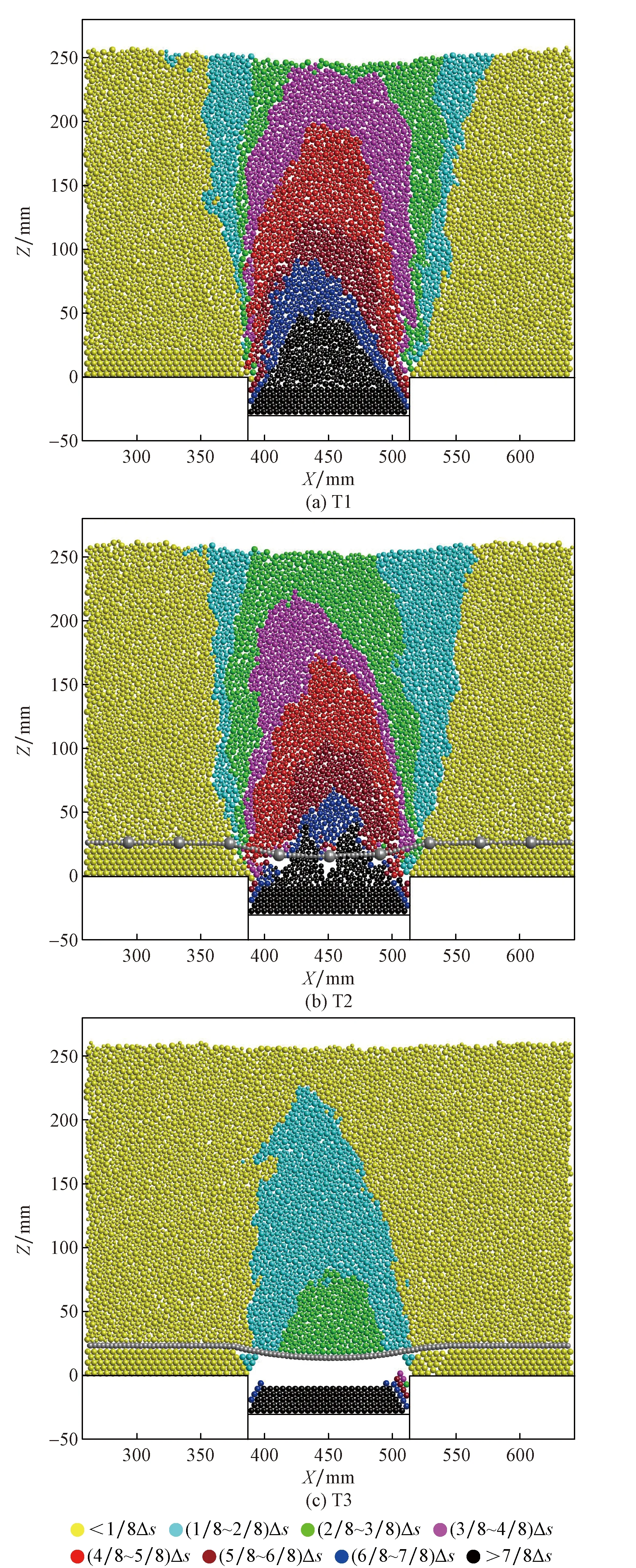
图9 土体填料沉降位移云图Fig.9 Settlement displacement clouds of soil fill

如图10所示为Δs=29.6 mm时土体表面沉降曲线,可以看出,加筋体的存在降低了土体表面的差异沉降,其中土工布为加筋体时土体表面差异沉降减少了65%,效果最好,而土工格栅则为15%,这是由于土颗粒穿过土工格栅室造成土体内部的沉降增加进而影响到土体表面。

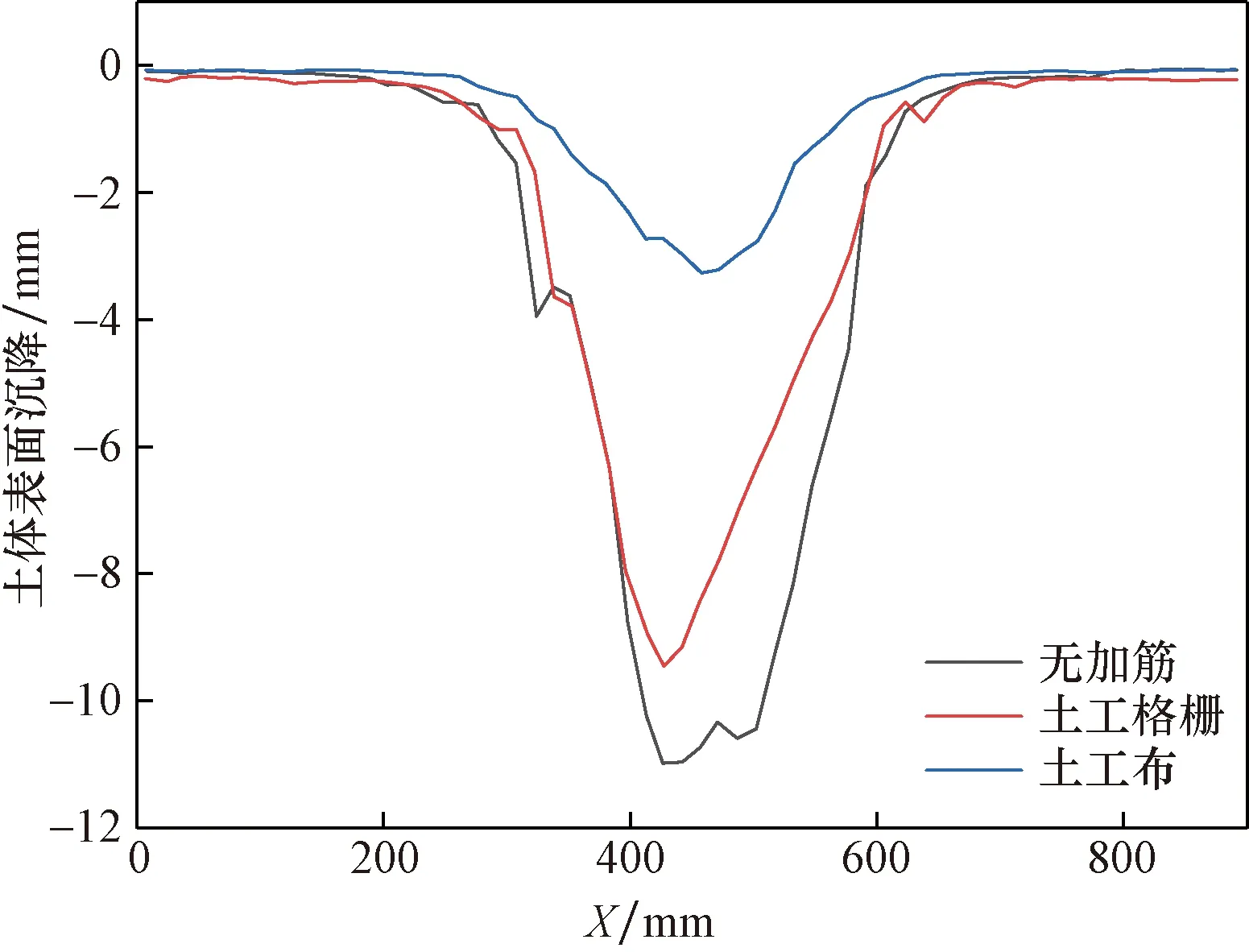
图10 土体表面沉降Fig.10 Soil surface settlement

3.3 力链分析

在MatDEM中,通过邻居矩阵和属性矩阵获得颗粒之间的接触情况,用矩形来表示颗粒接触点处合力的大小和方向,从而得到土体内部的力链图,通过力链图可以非常直观看到土体内部的传力结构。由MATLAB编程得到活动门下移29.6 mm时3种试验方案下的力链图,如图11所示,力链越粗表示接触力越大。可以看出,无加筋时,土体内形成了半椭圆形的土拱结构,在拱脚位置处发生了明显的应力集中,土体内应力重分布;对于加筋体为土工格栅时,节点受下沉土体作用使筋材内产生拉力,将活动门上土体荷载转移至两侧垫层,此时土体内形成了半圆形的土拱结构,土拱效应和拉膜效应共同工作;对于加筋体为土工布时,活动门上土工布受下沉土体作用发生变形产生拉力,将活动门上土体荷载转移至两侧垫层,此时土体内也形成了半圆形的土拱结构,土拱效应和拉膜效应共同工作。

如图12所示为Δs=0 mm和Δs=29.6 mm时活动门中心垫层以上沿土体高度的竖向应力变化。可以看出,各个数值试验的初始状态竖向应力曲线与理论值基本吻合,说明了制样的合理性,Δs=29.6 mm时,竖向应力曲线偏离初始状态值,活动门上土体荷载转移至两侧土体,土体内应力重分布。

图12 活动门中心垫层以上沿土体高度的竖向应力变化Fig.12 Evolution of vertical stress at the center of the trapdoor

如图13所示为Δs=29.6 mm加筋体拉力沿水平位置的分布情况。土工布和土工格栅的最大的拉

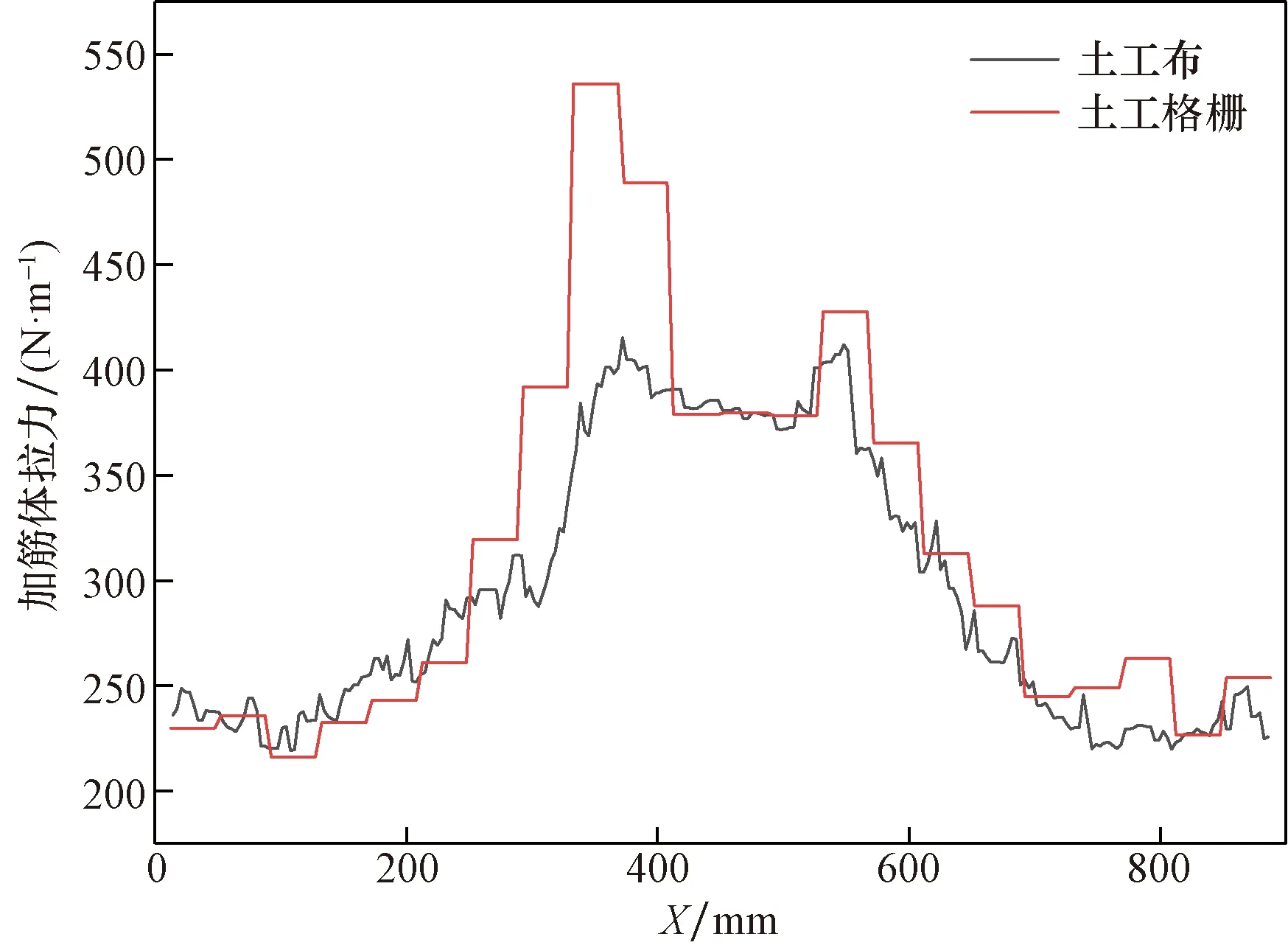
图13 加筋体拉力分布Fig.13 Distribution of tensile force

力都发生在活动门边界附近,在活动门范围内拉力基本保持不变,这与Han等[18]和Rui等[19]的研究一致。对于土工格栅,拉力在节点处会发生突变,这是由于土体对加筋体的作用力由节点颗粒承担。

由以上分析可知,含加筋时土体内土拱效应和拉膜效应同时存在,共同发挥荷载转移的作用,为了衡量拉膜效应对荷载转移的贡献情况,定义了拉膜效应贡献率Eg,公式为

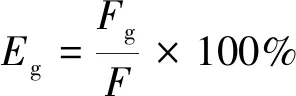
(3)

式(3)中:Fg为拉膜效应转移的荷载;F为土拱效应和拉膜效应一起转移的总荷载。

在数值模拟中加筋层位于垫层上表面,所以这里研究垫层以上土体中的土拱效应和拉膜效应。MatDEM中,给填料、加筋体和垫层颗粒进行分组,通过getGroupForce( )函数可以得到组与组之间的相互作用力。图14为活动门两侧各组之间的受力关系图,由关系计算得到最终状态时土工格栅和土工布的拉膜效应贡献率分别为40.78%和30.32%,说明加筋情况下土拱效应在荷载转移中发挥主要作用,这与杨广庆等[8]现场试验得出的规律相同,加筋体为土工格栅时,拉膜效应转移的荷载占比更大,这是由于颗粒穿过土工格栅室造成了土体内部土拱效应的退化。

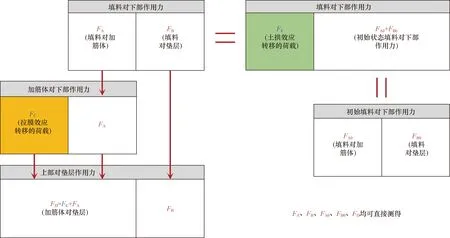
图14 活动门两侧各组之间的受力关系图Fig.14 Diagram of the force relationship between the groups on either side of the trapdoor

4 结论

基于室内模型试验进行了离散元数值建模分析,通过将双向土工格栅二维化的方式,从土拱率、位移、力链和加筋体受力的角度研究了不同加筋形式对土拱效应的影响,得到以下结论。

(1)加筋可以有效提升土体内的荷载转移效率,使用土工布比使用土工格栅更能保持土体内部土拱结构的稳定。

(2)加筋体的存在减少了土体内的差异沉降,降低了土体表面的差异沉降,其中土工布的效果最好。土工格栅的加筋方式下拱脚处为受力的薄弱点,容易对土拱结构的稳定性造成影响。随着活动门的下移,加筋层以上土体内形成了半圆形的土拱结构,土拱效应和拉膜效应共同工作。

(3)为了衡量拉膜效应对荷载转移的贡献情况,定义了拉膜效应贡献率,最终状态时土工格栅和土工布的拉膜效应贡献率分别为40.78%和30.32%,说明加筋情况下土拱效应在荷载转移中发挥主要作用,加筋体为土工格栅时,拉膜效应转移的荷载占比更大。