基于票价策略的民航和高铁演化博弈分析

孙博, 徐泽惠, 魏明,3

(1.中国民航大学空中交通管理学院, 天津 300300; 2. 中国民用航空飞行学院民航飞行技术与飞行安全重点实验室, 广汉 618300;3. 华设设计集团北京民航设计研究院有限公司民航机场安全与运行工程技术研究中心, 北京 100100)

民航与高铁是高速客运市场的两个运营主体,两种交通方式在部分主要客流通道同时存在,二者在经济性、便捷性、舒适性上各具优势,既存在竞争关系又存在合作关系。两种交通方式的票价机制、速度设置、运行方式和市场结构策略选取都会影响各自客运市场的旅客分配以及所产生的收益。民航与高铁若以实现自身和旅客利益最大化为目标,民航(高铁)的运营策略调整必然会影响高铁(民航)重新制定相应的针对性策略。因此,亟待剖析不同博弈策略下民航与高铁市场比例及其收益损失演变特征,对制定二者的市场策略具有重要的指导意义。

目前,学者们从不同视角研究了民航和高铁之间的关系,主要有如下3个方面。

第一方面,以旅客为主体分析民航与高铁之间耦合关系,如:韩震等[1]以大连北高铁站和周水子机场的旅客群体为研究对象进行敏感性及行为分析,通过仿真得出竞争区间内,民航和高铁可根据旅客时间和价格敏感度减少航班(列车)数量,形成“短途高铁,长途民航”的竞争态势;程谦等[2]调研南京—北京、南京—广州、南京—哈尔滨3条线路,应用多项Logit(multi-nominal Logit,MLN)和混合Logit模型(mixed Logit,ML)模型得出1 400 km 运距范围,中转时间在 1.5 h 以内,民航中转与空铁联运可以相互替代;孟海洋等[3]基于旅客时间价值理论模型得出短途旅行高铁具有优势而中长途民航有优势,且双方有效竞争空间距离以800 km为界限;Wang 等[4]基于中国民航与高铁多层网络,发现在仅存一种交通方式的城市中,来自耦合城市的旅客出行时间更短。

第二方面,研究民航与高铁定价策略及相互作用关系,如:Zhu等[5]以京沪通路为例得出,在民航与高铁的竞争关系中,民航通过提高准点率就可有效吸引客源;卓丽洪等[6]对民航与高铁价格弹性进行研究,得出在 800～1 500 km竞争区间内,铁路加权平均速度和价格对民航需求价格有显著的调节作用;Chen等[7]运用中国一个季度的货运数据得出开通高铁会减少中国航空货运量和航班频次;Li等[8]分析高铁向内陆快速扩张为航空业带来的负面影响;Liu等[9]运用数据包络分析(data envelopment analysis,DEA)法评估高铁发展对机场技术效率的影响;李晓津等[10]基于混合Logit模型和时间价值研究北京—太原—成都运输通道民航与高铁的定价策略,双方应充分利用大数据制定差异化的空铁联运产品价格。

第三方面,民航与高铁之间博弈关系,如:Raturi等[11]应用博弈论框架模拟印度高速铁路和航空公司之间的竞争,得出航司和高铁将以中等速度策略进行博弈;Li等[12]设置n种等级票价策略研究了高铁和航空公司之间在价格、利润和社会福利方面的竞争博弈,得出价格歧视程度的增加会削弱民航的竞争力;Mou等[13]在高铁提速前提下,京沪高铁和京沪航线之间竞争博弈区间将延长;骆嘉琪等[14]利用两阶段博弈模型探讨出民航与高铁在700～750 km的竞争区间内的均衡策略为(合作,合作);牟振华等[15]基于数值仿真探讨出行空铁抉择的动态演化,研究表明旅客偏向于选择高铁出行策略。此外,少数学者探讨了空铁合作的协同演进模式[16-17],得出民航与高铁合作的条件及利润、福利最大化这类联合机场制度的作用。由上可知,研究的不足之处主要有两个方面。一方面,现有文献缺少从两种交通方式的票价竞争与合作角度决定它们的客流分担率,进而影响其收益和损失;另一方面,现有文献多数以定性定量分析民航与高铁的竞争博弈关系,缺少针对二者合作关系进行动态演化仿真模拟。

现围绕基于票价策略的民航与高铁的博弈演化关系,从出行时间和费用角度,基于Logit模型刻画民航与高铁的客流分担率以及它们的收益和损失,为演化博弈提供数据支撑;构建基于票价策略的民航与高铁双方演化博弈模型,通过雅克比矩阵,求解双方博弈模型的5个均衡点,并分析其稳定性;通过计算机仿真,分析不同策略和初始博弈概率对两种交通方式的未来市场演变特征的影响。最后,以京哈通路为例,揭示民航和高铁之间不同定价策略对其收益的影响,据此帮助民航根据高铁的不同竞争和合作行为选择最佳的策略,从而验证该研究的有效性和正确性。

1 基于Logit模型的成本收益

影响旅客偏好选择民航与高铁出行的主要影响涉及票价、出行时长、准时性、舒适性和服务等方面。不失一般性,选取票价和出行时间两个最重要因素作为研究对象,基于Logit模型刻画两种交通方式的客运分担率,据此计算其收益和损失费用。

1.1 客运分担率

从始发地O到目的地D有民航(i=1)与高铁(i=2)两种可供旅客选择的运输方式,各自的客运分担率主要取决于票价、出行时间(在途、中转、延误和等待等)两方面因素。为了统一度量,引入时间经济价值函数V(t),将出行时间变量转变为出行费用,表达式为

(1)

式(1)中:r和v分别为全国居民年平均的可支配收入和工作时长。

在上述基础上,构建旅客选择民航与高铁的广义出行费用价值函数W1和W2,表达式为

W1=-{p1+[t1(wt)+t1(yx)+t1(yw)]V(t)}

(2)

W2=-{p2+[t2(yx)+t2(yw)]V(t)}

(3)

式中:p1为民航运输经济舱票价;p2为高速铁路二等座票价;t1(wt)为旅客在机场安检的平均时长;t1(yx)为民航运输运行时长;t2(yx)为高速铁路运行时长;t1(yw)为民航运输平均延误时长;t2(yw)为高速铁路平均延误时长。

根据旅客在某O-D对情景下民航和高铁广义出行费用,基于Logit模型估算两种交通方式的客运分担率fi,表达式为

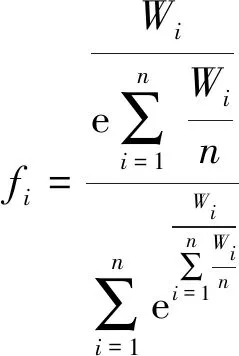
(4)

式(4)中:n=2。

1.2 成本与收益

考虑民航与高铁从投入到运营所需的基建成本、技术成本、环境成本、安全成本和运营成本,得出二者成本函数Ci为

Ci=Ci(jj)+Ci(js)+Ci(hj)+Ci(aq)+Ci(yy)

(5)

式(5)中:Ci(jj)为运输方式i的基建成本;Ci(js)为运输方式i的技术成本;Ci(hj)为运输方式i的环境成本;Ci(aq)为运输方式i的安全成本;Ci(yy)为运输方式i的运营成本。

考虑旅客支付及成本得出民航与高铁的收益函数Pi为

Pi=-WiQfi-Ci

(6)

式(6)中:Wi为旅客选择运输方式i获得的支付;Q为相同O-D总客流量。

1.3 超额收益

高铁与民航在相同O-D下选择单方合作或双方合作均会产生超额收益PT,主要体现在客流量的增加,从而进一步产生相应收益,即

(7)

式(7)中:Q′为因双方合作每日所增加的客流量。

2 民航与高铁演化博弈模型及分析

2.1 模型参数假设及构建

假定民航与高铁双方博弈主体均具有有限理性,二者均可选择合作或竞争策略。民航与高铁选择合作的概率分别为x和y,并进行参数假设,相关参数及含义如表1所示。

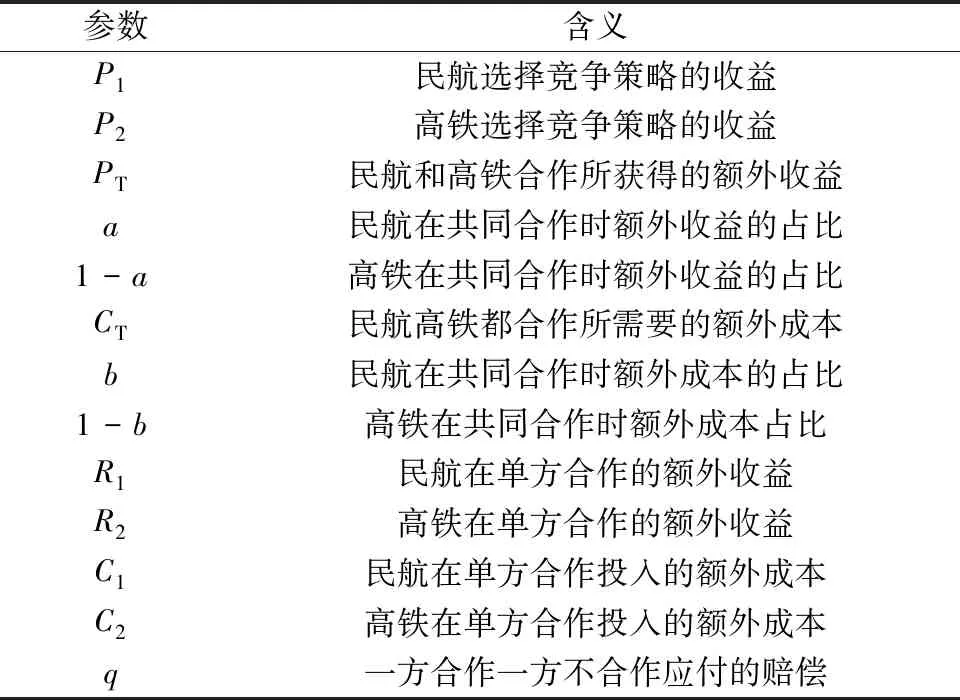
表1 模型参数及含义Table 1 The parameters and implications of the model

基于上述假设,分析民航与高铁在选择不同发展策略时的收益,并建立相应的演化博弈收益矩阵,如表2所示。

表2 民航与高铁演化博弈收益矩阵Table 2 Game payoff matrix between civil aviation and high-speed rail

令民航选择合作与竞争策略的期望收益分别为Em1和Em2,据此可计算其平均收益期望为Em,从而推导出双方博弈策略的复制动态方程F(x),如式(8)～式(11)所示。

Em1=P1+y(aPT-bCT)+(1-y)×

(R1-C1+q)

(8)

Em2=P1-yq

(9)

Em=P1+xy(aPT-bCT)+x(1-y)×

(R1-C1)+(x-y)q

(10)

R1+C1)+R1-C1+q

(11)

同理,可以计算高铁选择合作与竞争策略的期望收益En1和En2,平均收益期望En,以及其复制动态方程G(y),如式(12)～式(15)所示。

En1=P2+x[(1-a)PT-(1-b)CT+

(1-x)(R2-C2+q)

(12)

En2=P2-xq

(13)

En=P2+xy[(1-a)PT-(1-b)CT]+

(1-x)y(R2-C2)+(y-x)q

(14)

CT-R2+C2]+R2-C2+q}

(15)

综上所述,可以推导出其雅克比矩阵J,如式(16)～式(20)所示。

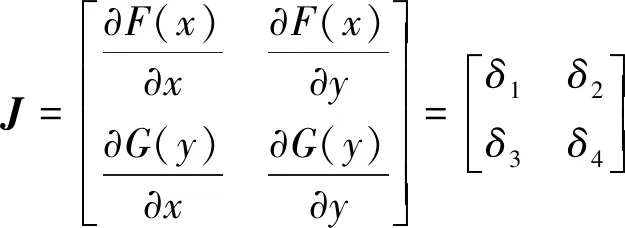
(16)

δ1=(1-2x)[y(aPT-bCT-R1+C1)+

R1-C1+q]

(17)

δ2=x(1-x)(aPT-bCT-R1+C1)

(18)

δ3=y(1-y)[(1-a)PT-(1-b)×

CT-R2+C2]

(19)

δ4=(1-2y){x[(1-a)PT-(1-b)×

CT-R2+C2]+R2-C2+q

(20)

2.2 模型求解

令民航和高铁选择合作与竞争策略的复制动态方程F(x)=0和G(y)=0可得到5个均衡点,分别为E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)、E5(x*,y*)。

均衡点相关值如表3所示。

表3 均衡点分析Table 3 Stability of equilibrium

根据均衡点的行列式和迹的数值影响局部稳定性相关结论,当det(J)>0,tr(J)<0时,该均衡点为民航和高铁双方演化博弈的稳定策略ESS;当det(J)>0,tr(J)>0,该均衡点不稳定;其余情况的均衡点均为鞍点。稳定性结论如表4所示,可知:均衡点(0,0)和(1,1)表现为两个ESS均衡点,分别表示民航与高铁同时选择竞争策略和同时选择合作策略;不稳定点(0,1)和(1,0)表示民航与高铁选择不同策略。

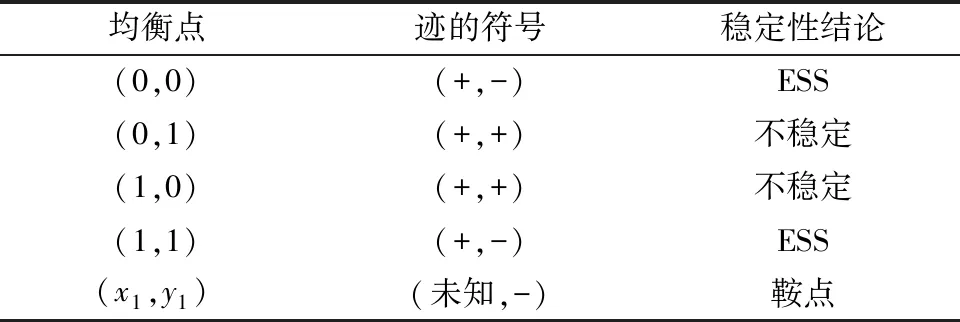
表4 稳定性分析Table 4 Stability analysis

高铁和民航双方合作策略演化相位图如图1所示,可知,两种交通方式的复制动态曲线都收敛于B和C两个稳定点,当双方都收敛于C时,竞争是常态,当双方都收敛于B时,合作是常态。O(x1,x2)为鞍点,是判断两条曲线是否收敛于B或C的关键点,取决于区域ACDO面积S1与区域ABDO面积S2的大小关系,若S2>S1时,博弈双方趋近于合作,反之则博弈双方趋向于竞争。

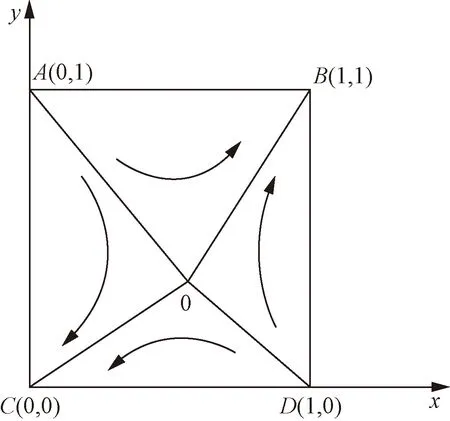
图1 民航与高铁的演化相位图Fig.1 Evolution phase diagram of civil aviation and high-speed rail

进一步地,分析参数S2的变化对双方演化策略选择的影响,如表5所示。

表5 博弈主体合作策略参数影响Table 5 The effect of parametric variation

可以看出,S2与民航和高铁选择单方合作的成本R1和R2呈负相关,可以理解为当双方合作成本超过一定限度时双方获取的利益小于成本,从而选择竞争策略。S2与民航与高铁选择双方合作的超额收益PT呈正相关关系,可以理解为当超额收益值增加时,民航与高铁双方倾向于选择合作策略。a和b分别为民航在双方选择合作时收益与成本占比,a增加时(1-a)减小,a减小时(1-a)增加,b与之相似,故无法判断a和b取值对S2的影响。其中S1、S2如式(21)和式(22)所示。

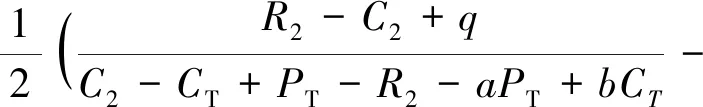
(21)

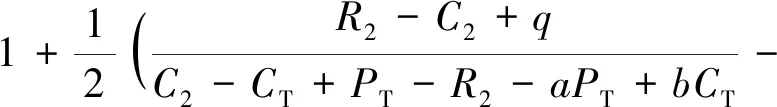
(22)

基于上述分析,民航和高铁之间演化双方策略会稳定于双方合作或双方竞争策略,并且参数的变化会影响策略演化进程。

3 实例分析与仿真

以北京—哈尔滨的通路为例,其日均客运量约为45.38万人。京哈航线全长1 050 km,票价为700～2 000元,飞行时长为1.25～2.42 h;京哈高铁全长1 198 km,票价为539～605元,运行时长为5.38～6.16 h。根据京哈通路的民航和高铁竞合关系,拟设计4种策略:①竞争策略1为民航低价票,高铁低价票;②竞争策略2为民航高票价短时长,高铁低票价长时长;③竞争策略3为民航正常票价短时长,高铁低票价高质量服务;④合作策略4为民航与高铁联合制定票价,合理划分运输网络与客流量。4种策略票价如表6所示,据此可以估算两种交通方式的客运分担率、收益损失情况。

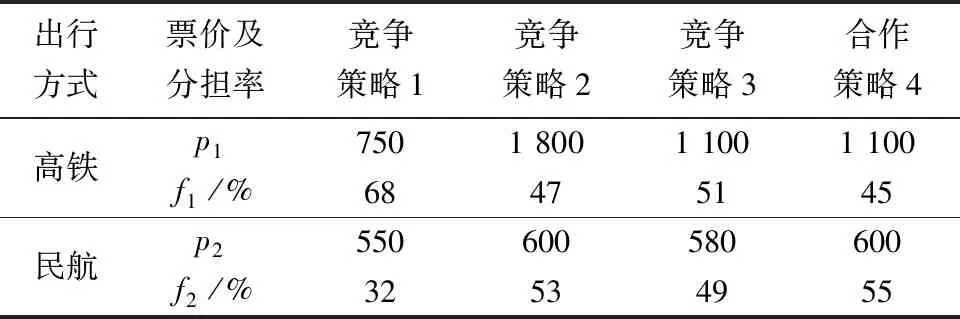
表6 民航与高铁的4种博弈策略Table 6 Four game strategies between civil aviation and high-speed rail

3.1 4种策略的博弈收益矩阵及稳定性分析

4种策略的稳定性分析及4种策略的稳定策略的收益如表7～表9所示,可知4种策略的鞍点分别为(0.23,0.02)、(0.35,0.15)、(0.45,0.13)、(0.47,0.01),求解得出稳定点均为 (0,0)和(1,1),可知,民航与高铁选择合作策略4下的双方收益最高,此时民航具有时间优势而高铁具有票价优,二者优势互补通过增加客流量来获取超额收益。民航与高铁选择竞争策略3的双方收益最少,虽然在票价设置上与合作策略类似,但双方无法利用自身优势在竞争中获取期望收益。当民航与高铁选择竞争策略1和2时,它们均可有效抵御对方的竞争威胁,通过各自采取比竞争对手的更低出行成本方式,从而获取更多的市场份额。

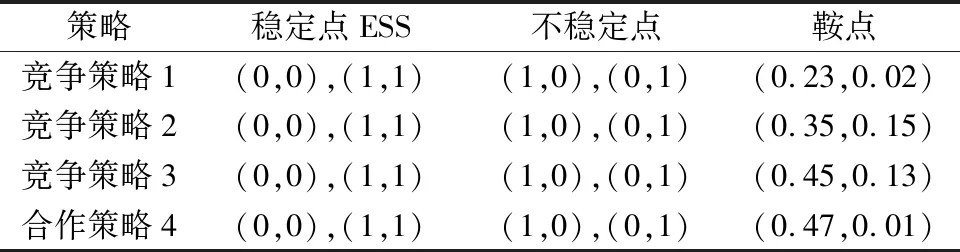
表7 4种博弈策略稳定性分析Table 7 Stability analysis of four strategies

表8 四种策略的稳定策略收益值Table 8 Profit of four strategies

表9 初始仿真参数Table 9 Profit of four strategies

3.2 4种策略的演化博弈分析

为了更准确模拟民航和高铁4种博弈策略演化情景以验证模型的有效性,假定4种初始合作策略概率(x,y),分别对应双方4种博弈策略进行动态仿真,部分参数如表9所示,仿真结果如图2～图6所示。

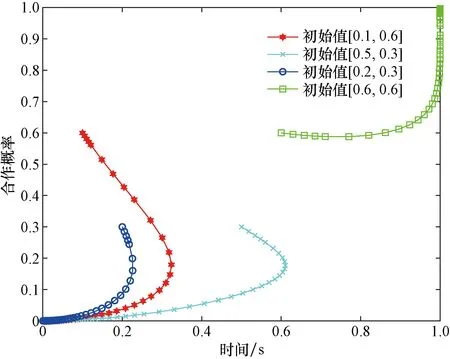
图2 4种演化策略的仿真结果Fig.2 The simulation result of four evolutionary strategies

图2刻画了4种策略下的不同初始合作概率如何影响双方最终的策略选择。若民航与高铁初始合作概率较低双方最终会趋于选择竞争策略,反之则趋于选择合作策略。

图3～图6具体探讨了4种策略的超额收益变化如何影响民航和高铁的最终演化结果,故令超额收益PT分别取值890万、1 000万、1 200万元。当在竞争策略1和2下,双方的初始合作概率均较高,双方合作增加的客流量会产生超额收益。因此随着超额收益增加,它们的最终选择从竞争策略转变为合作策略。在竞争策略3下,民航和高铁的初始合作概率均较低,因为不会改变超额收益的增加,最终选择继续保持竞争策略。在合作策略4下,双方的初始合作概率均较高,最终的策略选择不产生变化,并且趋向于合作策略的速率会随着超额收益的增加而加快演化速度。

图3 双方选择策略1的演化趋势Fig.3 Evolutionary path diagram of strategy 1

图4 双方选择策略2的演化趋势Fig.4 Evolutionary path diagram of strategy 2

图5 双方选择策略3的演化趋势Fig.5 Evolutionary path diagram of strategy 3

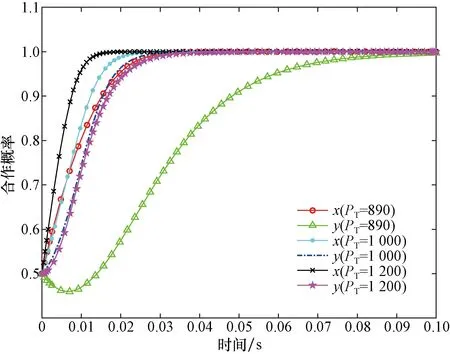
图6 双方选择策略4的演化趋势Fig.6 Evolutionary path diagram of strategy 4

4 结论

从票价角度探讨了基于演化博弈模型的民航和高铁之间竞争和合作关系分析,建立了Logit的客流分担率、出行博弈演化矩阵及其均衡稳定性分析等。最后,以京哈通路为例,计算4种票价策略下的收益损失情况,并探讨了不同情景下民航和高铁博弈策略的最终选择情况。研究表明:无论民航与高铁双方初始选择竞争策略或合作策略,只要初始合作概率和超额收益足够大,双方策略均会演化为合作策略。

然而,博弈模型未考虑不同旅客出行偏好、出行舒服度、准点率等对旅客出行选择的影响,据此民航和高铁需要不同组合策略以提升双方博弈收益,这是下一步的工作方向。