岩溶区燃气管道致灾概率分析:基于易损性-灾害系统集成视角
李乔楚, 陈军华
(1. 西南石油大学经济管理学院, 成都 610500; 2. 常州大学安全科学与工程学院, 常州 213164)
“碳达峰”“碳中和”明确了中国经济社会发展全面绿色转型的战略方向和目标要求,将成为生态文明建设的重要抓手。天然气作为清洁高效的优质化石能源被广泛应用于经济社会发展的诸多领域。岩溶塌陷主要源于地下土洞向上的逐步拓展,因此呈现显著的“隐蔽性”和“突发性”特征[1],对于通常采用埋地敷设的燃气管道工程,其日常运行不可避免地受到此类地质活动影响。与此同时,中国西南地区自然环境复杂脆弱、喀斯特地貌广布,暴雨等极端气候事件频发,断层带分布密集,在自然和人为因素耦合影响下极易诱发岩溶塌陷导致埋地燃气管道失效破裂,并进一步导致火灾、爆炸等次生灾害,对沿线居民的生命财产安全造成极大隐患,并且严重影响中国能源系统的清洁低碳转型进程。因此,有必要科学准确地评估岩溶区燃气管道的致灾概率,为灾害应急响应和救援工作提供理论指导。
近年来,中外学者开始着眼于燃气管道的致灾概率分析。Qiu等[2]构建了城市燃气管道泄漏事故跟踪与致灾概率预测模型,首先基于鱼骨图模型和蝴蝶节模型厘清事故灾害的演化逻辑,然后结合突变理论得到条件概率表,最终利用动态贝叶斯网络模型的强大推理能力研判致灾概率及发展趋势。Brito等[3]利用结合效用理论和消去-选择转换树(ELECTRE TRI)模型的集成方法,基于实际案例测度了燃气管道灾害的发生概率。王春雪等[4]构建了城市燃气管道泄漏致灾混合概率风险评估模型,在基于模糊理论得到根事件先验概率基础上进一步结合贝叶斯网络理论推算出燃气管道泄漏的致灾概率。王文和等[5]构建了城市地下燃气管网致灾概率动态分析模型,在失效蝴蝶结模型基础上进一步构建贝叶斯网络模型,并结合历史经验数据动态模拟喷射火、蒸汽云爆炸、闪火等事件的发生概率。陈军等[6]构建了燃气管网燃爆概率风险评估模型,结合马尔科夫理论链接灾害演变过程与时间发展进程,并结合动态贝叶斯网络模型推算了燃气管道泄漏扩散后的火灾、爆炸概率。
上述研究为燃气管道致灾概率评估提供了有效参考,但在以下方面仍有所局限性:一是现有研究主要立足于管道失效过程,结合“人-物-环-管”等维度剖析燃气管道的致灾事件,缺乏结合灾害系统理论的全面分析,往往难以实现致灾概率的准确测度。二是现有研究大多仅着眼于事件危险性分析,没有考虑到管道易损性这一重要因素,从而忽略了管道抗外载能力对致灾过程的重要影响。鉴于此,现提出一种基于易损性-灾害系统集成视角的岩溶区燃气管道致灾概率分析方法。一方面结合灾害系统理论从孕灾环境活跃性、灾害因子风险性、承灾体脆弱性多重维度全面分析岩溶区燃气管道的致灾事件体系,结合贝叶斯网络的信念传播更新优势逐层推算致灾事件的危险概率;另一方面考虑到管道易损性水平与灾害种类和强度、管道结构和功能、灾害和管道时空配置等方面的关联关系,结合可靠度分析理论,立足于有限元模拟结果和聚乙烯管道特性构建数理模型,从灾害损伤强度和抵抗灾害能力两者的交互作用视角综合核算管道的易损概率,并将其与致灾事件危险概率相结合,创新“事件危险性+管道易损性”的研究范式,进一步完善管道灾害的风险评价思路,为岩溶区燃气管道致灾概率的科学、准确、全面评估提供理论依据。
1 致灾事件危险性分析
事件危险性的定义为威胁影响区域内人员、物体安全的各类致灾事件的发生概率,即致灾风险源转变为灾害危险事件的概率分布。
1.1 危险性评价指标体系构建
结合灾害系统理论,从孕灾环境活跃性、灾害因子风险性和承灾体脆弱性3个方面构建危险性评价指标体系,具体如表1所示。

表1 危险性评价指标体系Table 1 Hazard assessment index system
1.2 先验概率确定
现阶段,考虑到岩溶区燃气管道的失效数据库尚未建立,且结合统计分析模型开展基本事件的失效概率评估往往难以保证准确性和适用性,因此通常需要结合专家经验确定事件的失效可能性,但对于一些诱发燃气管道灾害的模糊性事件,例如“受教育程度不高”“管道保护意识淡薄”等具有不确定性和随机性,即使是专家也仅能针对发生概率给出模糊性语言。模糊数学则是解决已知数据不足、量化专家评估意见的良好方法[7],故将引入模糊数学理论确定岩溶区燃气管道致灾事件的先验概率。
1.2.1 专家权威性确定
考虑到专家知识水平、经验程度、信息来源、公正程度等不同会导致决策差异性,因此建立如图1所示的专家权威性评估层次分析模型[8],基于专家综合能力权重修正评估意见,促使评估结果更加符合客观实际。采用一种基于“指数标度”的改进层次分析法确定权重[9],指数标度如表2所示。

图1 专家权威性评估层次分析模型Fig. AHP model for expert authoritative evaluation

表2 指数标度Table 2 Index scale
1.2.2 隶属度函数确定
在模糊数学理论中,模糊语言值反映了各个指标对应的事件危险性大小,将各个指标的评估结果划分为五级递阶变化的事件危险性等级,即为低(L)、较低(RL)、中等(M)、较高(RH)、高(H)。基于此,进一步将各个指标对应的事件危险性等级转化为梯形模糊数,模糊数对应的隶属度函数模型如式(1)所示。

(1)
式(1)中:a和b分别为模糊数的上下限。

1.2.3 模糊数概率化
基于专家评估意见的模糊数函数是介于[0, 1]内的模糊集合,需要将其转化为一个清晰值,即模糊可能性值(fuzzy possibility score,FPS),FPS表征专家对某一事件发生可能性的信任度。基于左右模糊排序法将模糊数转换为模糊可能性值[10],其定义的最大模糊集和最小模糊集分别为
(2)
(3)
基于此,模糊数的左右模糊可能性值分别为
(4)

(5)
式中:fW(x)为模糊数W对应的隶属度函数;W为致灾可能性等级对应的模糊数;sup表示集合的上确界;∧表示模糊数学理论中的“取小”运算。
模糊数的模糊可能性值FPS为
FPS=[FPSR(W)+1-FPSL(W)]/2
(6)
在得到各评估指标的模糊可能性值后,即可将其转化为模糊失效率[11],即各基本事件的先验概率为
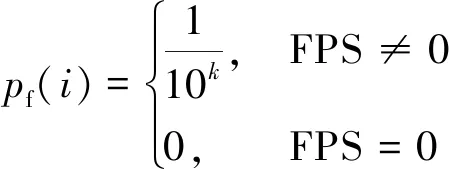
(7)
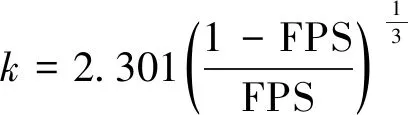
(8)
1.3 危险概率计算
故障树法被广泛应用于油气管道危险事件的概率分析,但故障树法基于最小割集的计算过程较为烦琐,若采用计算机解算则会受到有效计算位限制,导致研究结果产生显著偏差,而在贝叶斯网络(Bayesian network,BN)中事件发生概率的计算可等效为信念的传播和更新,计算过程简便且结果更加精确[12],因此选用贝叶斯网络评估岩溶区燃气管道致灾事件的危险性。
假设贝叶斯网络中根节点为X1,X2, …,XM,中间节点为F1,F2, …,FN,叶节点为Top,以上事件组成了贝叶斯网络中的随机变量集合{X1,X2, …,XM,F1,F2, …,FN, Top},记为V={V1,V2, …,VK}。由于贝叶斯网络是基于概率推理的数学模型[13],故联合概率P(V)=P(V1,V2, …,VK)可表示为
P(V)=P(V1,V2,…,VK)
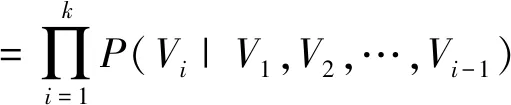
(9)
根据条件独立性假设,联合概率分布即可简化为
P(V)=P(V1,V2,…,VK)
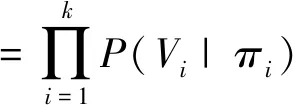
(10)
式(10)中:πi为节点Vi的父节点集。
将先验概率和条件概率表代入联合概率分布,即可求得最高层事件的发生概率,即岩溶区燃气管道致灾事件的危险概率为
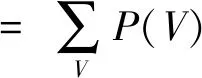

(11)
式(11)中:vi为节点Vi的取值。
2 燃气管道易损性分析
易损性最早用于描述飞机、船体等军事装备对于物理碰撞的脆弱程度[14],近年被推广至灾害研究领域。管道易损性定义为:在给定破坏情景下,管道达到或超出损伤临界状态的概率。管道易损性水平与灾害类型和强度,管道结构和功能,灾害与管道的时空配置关系及人类社会的防灾、减灾能力密切相关。将易损性理论引入岩溶区燃气管道灾害的致灾可能性分析,以概率形式定量评估灾害因子强度和管道承灾能力间的关系,有助于准确把握管道抗外载能力对致灾过程的重要影响。
2.1 易损函数构建
对于岩溶区燃气管道,其易损性由两方面因素决定[15]:一是灾害载荷对管道的损伤强度;二是管道自身抵抗灾害损伤的能力,易损性函数可表示为
M=f(DR,DS)
(12)
式(12)中:M为管道易损性;DR为管道抵抗灾害能力;DS为灾害载荷损伤强度。
由于管道易损性概率对应于结构可靠度理论中的失效概率,为了更加直观地表征易损性概念,即概率越大管道越容易发生损伤,针对可靠度理论的极限状态函数进行调整,进一步得到管道易损性函数为
M=f(DS,DR)=DS-DR
(13)
当外载荷损伤强度大于管道抗损伤能力时即发生管道失效,则易损概率函数可进一步转化为
P(M>0)=P{(DS-DR)>0}
(14)
2.2 评估指标选取
遵循代表性、客观性、可获得性等评价指标选取原则,选取岩溶土体塌陷长度(CSL)、岩溶土体塌陷宽度(CSW)、岩溶覆盖层厚度(KOT)、管道壁厚(PWT)、管道埋深(PBD)、土体弹性模量(SEM)、管土摩擦因数(FC)、管道服役时间(PSL)8个指标开展管道易损概率的评估,8个指标的参数值分别用m1、m2、m3、m4、m5、m6、m7、m8表示。
结合工程实际以及前期研究得到的影响因素作用规律[16],岩溶土体塌陷长度、岩溶土体塌陷宽度、管土摩擦因数、土体弹性模量越大,岩溶覆盖层厚度越小,岩溶塌陷对管道的损伤强度(DS)越大;选用厚壁管道、适度增大埋深,管道服役时间越短,管道抵抗损伤能力(DR)越强,因此可得
(15)
2.2.1 岩溶土体塌陷参数
岩溶土体塌陷长度和宽度越大,管道随土体产生的位移越大,承受的土体作用载荷也越大,因此管道越容易发生失效破坏;岩溶覆盖层厚度越大,地下岩溶土洞发育时上部土体结构越稳定、下沉量越小,管道在土体作用下产生的力学响应也越小。
设定在某一具体研究情景下导致管道失效破坏的临界岩溶土体塌陷参数分别为CSLs、CSWs和KOTs,当岩溶土体塌陷长度等于CSLs、岩溶土体塌陷宽度等于CSWs或岩溶覆盖层厚度等于KOTs时,管道处于临界失效状态。结合有限元模拟得到的敏感参数影响规律,定义岩溶土体塌陷长度易损性变量、岩溶土体塌陷宽度易损性变量、岩溶覆盖层厚度易损性变量分别为
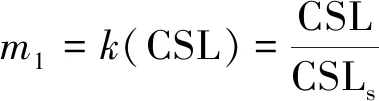
(16)
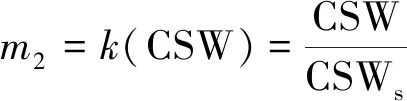
(17)
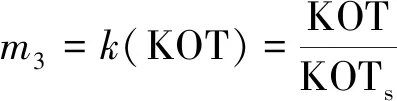
(18)
2.2.2 管道壁厚
壁厚是决定管道安全性能的关键因素,壁厚越大管道的径厚比相对越小,管道刚度越大。设定在某一具体研究情景下管道发生失效破坏时对应的临界管道壁厚为PWTs,当壁厚等于PWTs时,管道处于临界失效状态。结合有限元模拟得到的敏感参数影响规律,定义管道壁厚易损性变量为

(19)
2.2.3 管道埋深
管道埋深的增加有利于增强土拱效应,减小岩溶塌陷范围从而降低其破坏能力;但基于前期研究[16]结果,深埋管道(>1.5 m)承受的岩溶土体压缩作用持续增加,带动压缩应力出现陡增,且深埋管道更易受到地下土层错动的直接影响,因此在穿越岩溶区域时应选择合适的埋深以保证管道安全。设定在某一具体研究情景下管道发生失效破坏时对应的临界埋深为PBDs,当埋深等于PBDs时,管道处于临界失效状态。结合有限元模拟得到的敏感参数影响规律,定义管道埋深易损性变量为

(20)
2.2.4 土体弹性模量
设定在某一具体研究情景下管道发生失效破坏时对应的临界土体弹性模量为SEMs,当土体弹性模量等于SEMs时,管道处于临界失效状态。结合有限元模拟得到的敏感参数影响规律以及后续研究的岩溶土洞尺寸范围,定义土体弹性模量易损性变量为
(21)
2.2.5 管土摩擦因数
管土摩擦因数增大将直接导致土体摩擦阻力越强,增大岩溶塌陷作用下埋地管道危险截面的应力集中,因此在经济允许的前提下应选用摩擦因数较小的土体进行管沟回填。设定在某一具体研究情景下管道发生失效破坏时对应的临界管土摩擦因数为FCs,当管土摩擦因数等于FCs时,管道处于临界失效状态。结合有限元模拟得到的敏感参数影响规律,定义管土摩擦因数易损性变量为
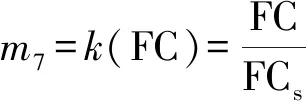
(22)
2.2.6 管道服役时间
随着服役时间的逐年增加,老化现象将导致管道自身强度显著下降,因此服役时间成为影响管道易损性的关键参数。设定在某一具体研究情景下管道的设计使用寿命为PSLs,当服役时间等于PSLs时,管道处于临界失效状态。结合有限元模拟得到的敏感参数影响规律,定义管道服役时间易损性变量为

(23)
2.3 易损概率计算
基于可靠度评估方法开展易损概率测算,通过常用方法的优缺点对比,选用在平均值处功能函数展开较为合理的设计演算点法开展后续研究。
首先引入可靠度指标β,假设易损性函数M服从正态分布,其平均值为μm,标准差为σm,其易损概率[17]为

(24)
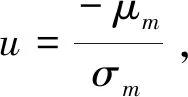
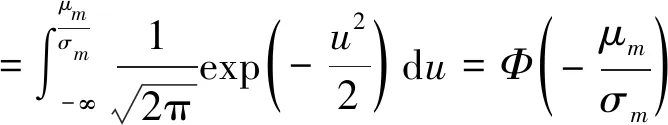
=Φ(-β)=1-Φ(β)
(25)
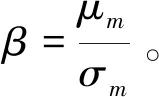
基于设计验算点法可以计算得出管道可靠度指标β,通过查阅标准正态分布表即可得到与之对应的易损概率P(M),如图2所示[18]。
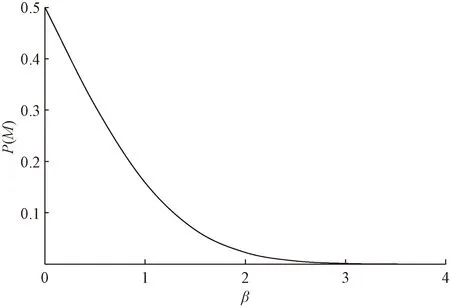
图2 易损概率与可靠度指标关系图[18]Fig.2 Relationship between vulnerability probability and reliability indicator[18]
3 案例分析
贵州X岩溶区段位于纳雍-开阳东西向构造带与织金北东向构造带的交汇处,在内外营力的共同雕塑下区段内形成了千姿百态的喀斯特地貌景观。近年来,在矿山无序开采、地下洞穴发育、持续强降雨及地震活动等多重因素影响下,每年发生明显地面塌陷40余次,并愈发呈现出增强趋势。选择该区段内一埋地燃气管道项目作为研究案例,管材类型为PE80,密度为950 kg/m3,管径为200 mm,壁厚为18.2 mm,瞬态松弛模量为578.71 MPa,运行压力为0.4 MPa,埋深为 1 m。
3.1 危险概率计算
聘请来自燃气管道设计、施工、管理、安全风险评价、灾害救援、灾害防治等不同领域的6位专家共同组成专家评估小组。通过专家权威性评估层次分析,得到各位专家的评估能力权值w=(0.172 0, 0.142 2, 0.171 5, 0.192 8, 0.144 1, 0.177 3)。聘请专家依据自身工作领域内的知识和经验完成各基本事件的危险性等级评估,并基于隶属度函数对专家模糊评价语言进行量化,从而确定各基本事件的模糊概率。
以“X1受教育程度不高”为例,结合专家评估小组针对这一基本事件的危险性等级评估结果,进一步得到考虑各位专家评估权威性的模糊数W为
W=max[wc1fLα∧wc2fLα∧wc3fRLα∧wc4fRLα∧wc5fLα∧wc6fRLα]
=[0.172 0×0+0.142 2×0+0.171 5×(0.15+0.1α)+0.192 8×(0.15+0.1α)+0.144 1×0+0.177 3×(0.15+0.1α),0.172 0×(0.25-0.1α)+0.142 2×(0.25-0.1α)+0.171 5×(0.45-0.1α)+0.192 8×(0.45-0.1α)+0.144 1×(0.25-0.1α)+0.177 3×(0.45-0.1α)]
=[0.081 252+0.054 168α,0.358 336-0.1α]
(26)
结合模糊集拓展理论,模糊数W对应的专家权重综合评价函数为
(27)
结合式(2)~式(6),计算得到左模糊可能性值FSPL(x)=0.871 5,右模糊可能性值FSPR(x)=0.325 8,综合两者得到模糊可能性值FSP=0.227 1。结合式(7)和式(8),最终得到基本事件“受教育程度不高”的先验概率值pj(1)=0.000 3。
同理,对剩余危险事件的先验概率进行计算。接下来,根据贝叶斯网络计算法则针对各层节点的概率分布进行逐步计算,具体结果汇总于图3,其中代码与表1相对应。最终,计算得到ZJ岩溶区段燃气管道致灾事件的危险概率P(Top=1)=0.032 2。
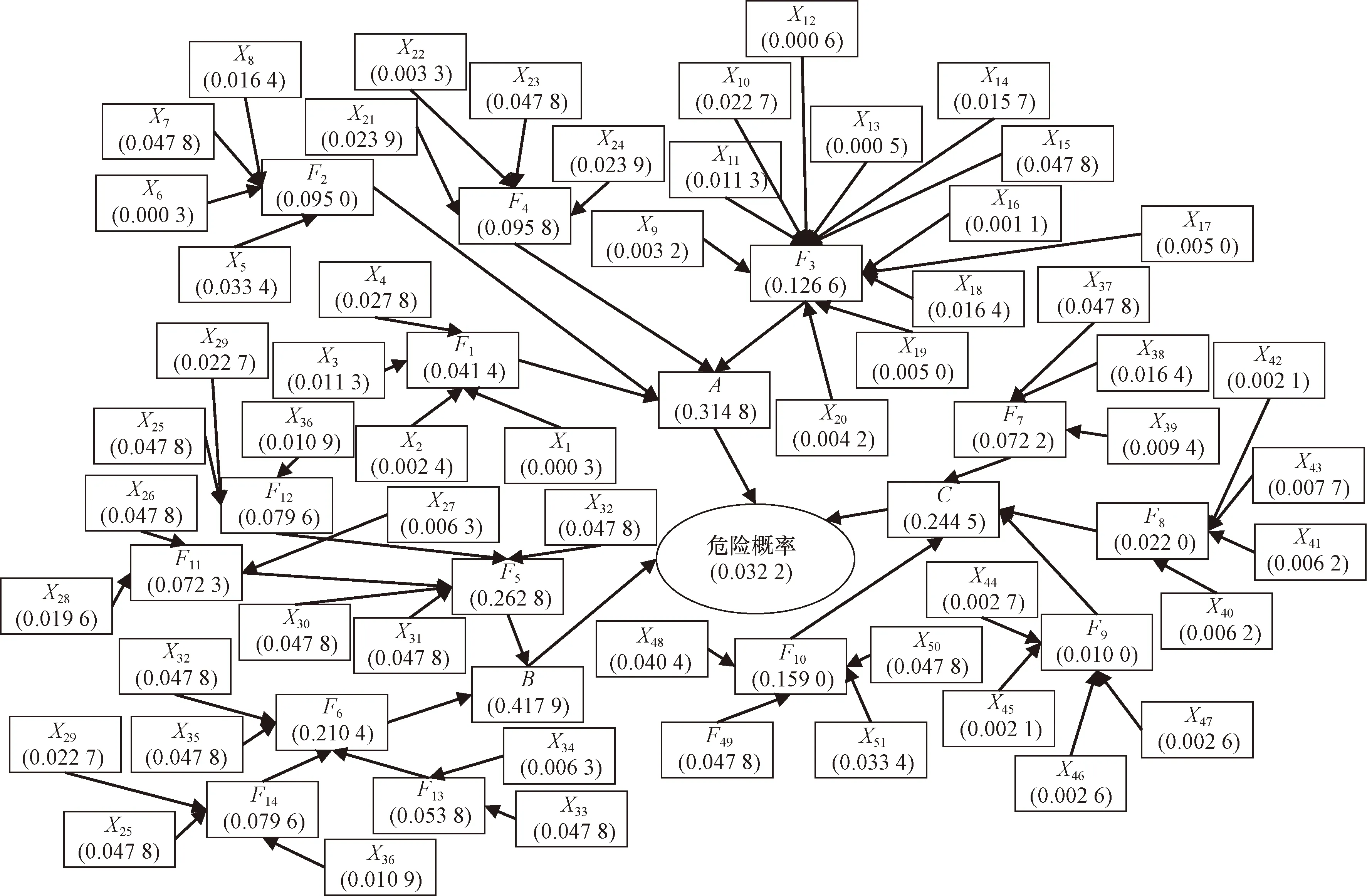
图3 基于贝叶斯网络的计算结果Fig.3 Calculation results based on Bayesian network
3.2 易损概率计算
基于所构建的岩溶区燃气管道易损函数,为了确定各易损性指标的临界数值,基于ABAQUS软件构建了图4所示的岩溶塌陷区埋地管道的有限元模型[16],采用4节点Shell单元、8节点3D-Solid单元分别对管道和土体进行离散建模,基于Prony级数建立PE80管材的本构方程,选用Mohr-Coulomb模型描述岩溶土体的非线性特征。结合研究区域岩溶勘探的实际数据和管道工程的具体参数确定参数取值范围,具体汇总于表3。
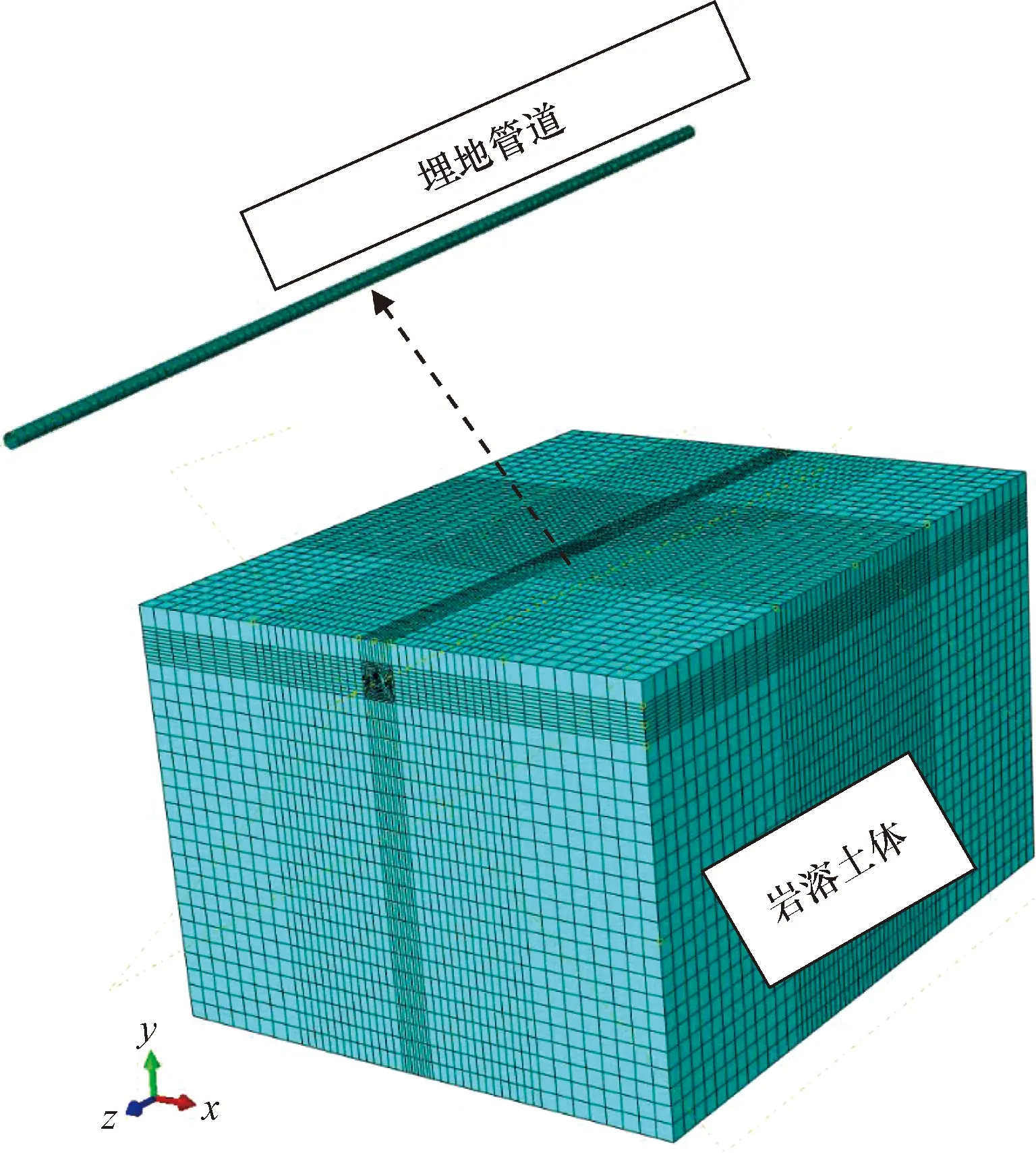
图4 岩溶区燃气管道有限元模型Fig.4 Finite element model of gas pipeline in karst area
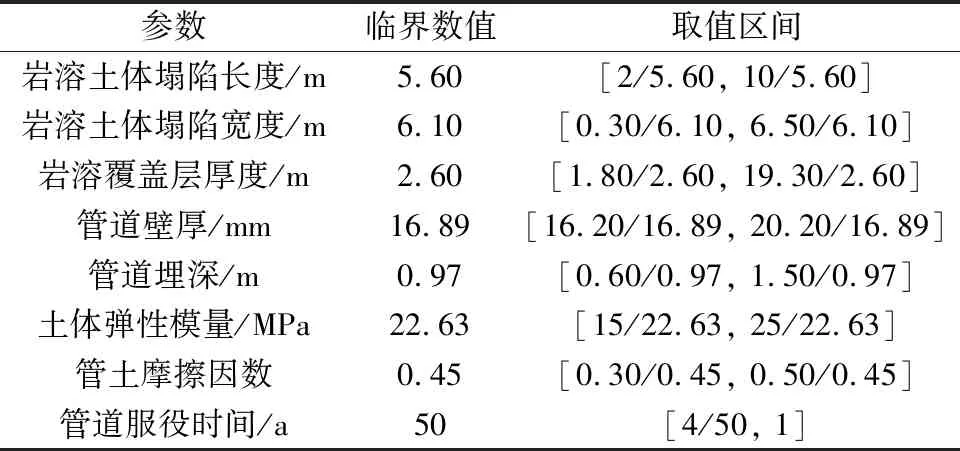
表3 易损概率计算基础数据Table 3 Basic data of vulnerability probability calculation
基于设计验算点法的相关理论,结合MATLAB编程分别编制相应计算程序。模型计算迭代次数为11,最终计算得出的可靠度指标β为1.968 2,通过查阅标准正态分布表,得到基于设计验算点法的岩溶区燃气管道易损概率P(M)=0.026 9。
3.3 致灾概率计算
从“致灾事件危险性”和“燃气管道易损性”两个维度综合衡量ZJ岩溶区段燃气管道的致灾可能性,即致灾概率P=P(Top=1)P(M)=0.032 2×0.026 9= 0.866 2×10-3。根据美国石油协会标准《API 581—2008 Risk-Based Inspection Technology》[19]即《API 581—2008基于风险的检测技术》以及挪威船级社标准《DNV-RP-F 116 Integrity management of submarine pipeline systems》即《DNV-RP-F 116海底管道系统完整性管理推荐作法》[20],ZJ岩溶区段燃气管道致灾概率等级为三级(偶尔发生),属于不可接受等级,需根据成本与效益对岩溶发育程度、管道安全水平、灾害演化趋势等开展持续监测与科学评估。
4 结论
基于灾害系统理论,从孕灾环境活跃性、灾害因子风险性、承灾体脆弱性多重维度全面分析岩溶区燃气管道的致灾事件体系;在构建故障树模型基础上进一步转化为贝叶斯网络模型,将事件发生概率计算等效为信念的传播和更新,弥补故障树模型有效计算位限制和计算过程烦琐等问题,有利于结合系统性视角更为简便、准确地测度致灾事件的危险概率。
考虑到管道易损性水平与灾害种类和强度、管道结构和功能、灾害和管道时空配置等方面的关联关系,将易损性理论运用到岩溶区燃气管道致灾概率分析,结合可靠度分析理论通过概率形式定量分析灾害事件下管道的易损程度,从而更为直观地衡量岩溶塌陷损伤强度和燃气管道抵抗能力之间交互作用,有利于准确评估管道抗外载能力对致灾过程的重要影响;与此同时,将基于有限元模拟构建的数理模型以及岩溶勘探实际数据嵌入致灾可能性分析过程,能够在一定程度上弥补以往研究主要基于专家经验造成的评估主观性问题。
在故障树分析基础上构建岩溶区燃气管道灾害贝叶斯网络,基于岩溶勘察和实地调研数据,结合模糊理论针对贝叶斯网络各层节点的概率分布进行逐步计算,得到致灾事件的危险概率为0.032 2;结合有限元模拟结果和聚乙烯管道特性,将可靠度分析理论运用到岩溶区燃气管道易损性评价中,基于设计验算法得到燃气管道的易损概率为0.026 9。从“致灾事件危险性”和“燃气管道易损性”两个维度综合衡量ZJ岩溶区段燃气管道的致灾可能性,最终得到致灾概率为0.866 2×10-3,属于不可接受等级,需根据成本与效益对岩溶发育程度、管道安全水平、灾害演化趋势等开展持续监测与科学评估。

