基于耦合欧拉-拉格朗日方法的水下结构物碰撞分析①
□□ 魏 鑫,刘 炜
(1.山西省交通建设工程质量检测中心(有限公司),山西 太原 030006;2.山西工程科技职业大学 建筑工程学院,山西 晋中 030619)
引言
随着海洋油气开发中的水下生产系统或技术发展,种类繁多的水下设施在深水和浅水中均得到广泛应用。水下设施是一种固定式的海洋工程结构物,由于其位于海底,检修和维护十分不便,因而在设计时应保证其在水下长时间服役过程中的结构可靠性[1]。传统的水下设施结构设计较为注重常见载荷下的结构杆件分析,而在结构物服役过程中,可能发生许多突发工况,如平台落物、渔网拖拉和基础冲刷等,水下结构物在这些工况下也应保证其结构完整性。由于这些突发工况为动态问题,并伴有大量的结构非线性和大变形问题,采用传统的理论计算和静态有限元方法无法进行分析,同时在实验室进行模型试验的造价较高,并与真实工况存在偏差。因此,采用耦合欧拉-拉格朗日(Coupled Eulerian-lagrangian,CEL)有限元方法来处理海洋工程和水下工况方面存在的大变形和瞬态问题已经逐年增多[2-3]。
1 理论分析
某海上生产项目采用平台加水下生产设施的开发模式,其中其浅水工程中心处理平台周围有多个水下设施,这些水下设施提供了水下关断隔离阀系统,当平台发生突发状况时,切断管道天然气供应,从而保证中心平台的安全性。但是由于距离平台太近,这些水下设施均面临着平台操作和生产过程中落物碰撞的危险。经过风险分析,需要对于某种特定案例进行分析,假定平台上有1个长、宽、高均为1 m,壁厚为10 mm的水罐掉落,检查最小的水下设施结构完整性,该水下设施的碰撞区域为1.5 m的正方形顶板,厚度为10 mm。按照DNV-RP-C204规范[4],海洋工程结构物需按照突发工况下设计的推荐做法。按照该规范,突发工况下结构变化通常与能量的耗散相关,并伴有弹性范围的结构大变形和应变,并明确指出可以采用非线性动态有限元进行分析。落物载荷的特征是产生动能[5],该动能由落物的质量和碰撞发生时的速度决定。动能一般由发生碰撞部件的应变能进行耗散。平台上落物速度与落下高度和水深均有关系。当水足够深时,由于水的浮力和阻尼影响,最终落物以恒定速度下落。该特征距离和最终落物速度计算见式(1)和式(2):
(1)
(2)
式中:sc——特征距离;
m——落物质量;
a——水动力附加质量;
ρw——海水密度;
Cd——水动力拖曳系数;
Ap——落物的投影横截面积;
vt——最终速度;
V——落物的位移。
虽然规范中给出了一些特定情况下的碰撞分析方法,但对于水箱掉落的情况未涉及,因而需要采用非线性动态有限元方法进行分析。根据以上公式,假定水箱中有1/4的淡水,由于水深已经超过了公式中的特征距离,计算得到最终的水箱速度为5 m·s-1,水罐的动能计算见表1。

表1 动能计算结果
2 有限元模型
采用通用有限元软件建立有限元模型,该软件中CEL方法已在跌落和碰撞研究中得到了广泛应用[2,6-7]。该有限元模型包括罐体、水以及结构顶板,如图1所示。罐体和顶板均采用壳单元,水采用欧拉单元。罐体和顶板、罐体和水之间为通用接触。采用显示分析计算三者之间的碰撞响应,整体计算时间为36 ms。罐体材料为常见的Q235钢板,水下设施顶板为DH36钢板,采用双线性材料模型。水的材料属性采用状态方程进行描述[6]。有限元模型中的材料属性见表2。边界条件及载荷如下:顶板的四周固定,并在罐体和水单元上施加5 m·s-1的速度载荷。由于罐体同时受到浮力和重力作用,因而仅在罐体上施加非常小的加速度载荷;而水则施加重力加速度载荷。罐体和顶板、罐体和水之间建立外部接触属性,法向为硬接触,不考虑侧向摩擦。碰撞下考虑钢材的延性渐进破坏[8],当应变值高于极限值时,通过设置塑性位移为0来设置结构的破坏。
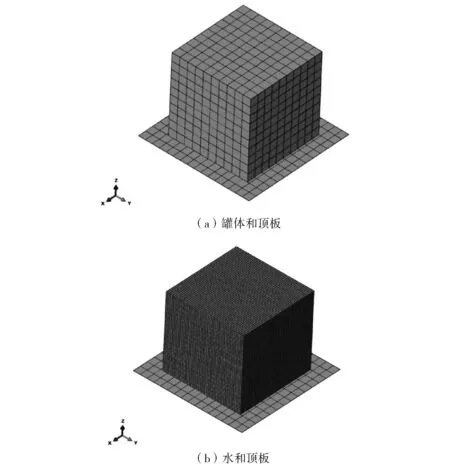
图1 有限元模型
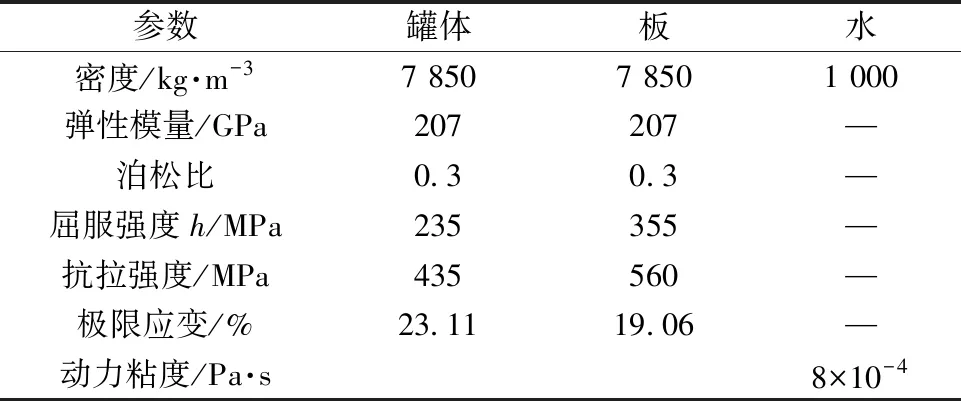
表2 材料属性
3 计算结果
能量耗散包括三部分,包括罐体内能、顶板内能以及水动能。内能主要是由结构变形产生的,包括弹性应变能和塑性应变能;而水的内能则是在碰撞过程中水面被激发而导致的速度改变。
在碰撞过程中部分动能转化为内能,如图2所示。从图中可见,在碰撞后的10 ms内,总内能变化较为剧烈,而后则基本保持在4 kJ。顶板的内能变化波动较大,而罐体的内能则保持稳步上升趋势。最终,顶板和壳体的内能值基本相当。动能随时间的变化如图3所示。总动能为6 kJ,与前面的理论计算一致,在前30 ms内的动能损失为3 kJ。在碰撞发生时,罐体和水的动能迅速见效,顶板的动能在碰撞瞬时增加然后迅速降低,数值基本在可忽略的范围内。罐体的动能保持在1 kJ。在前15 ms内,总动能和水的动能变化基本相似,而15 ms后水的动能则一直增加,并成为总动能的主要部分。

图2 内能随时间的变化
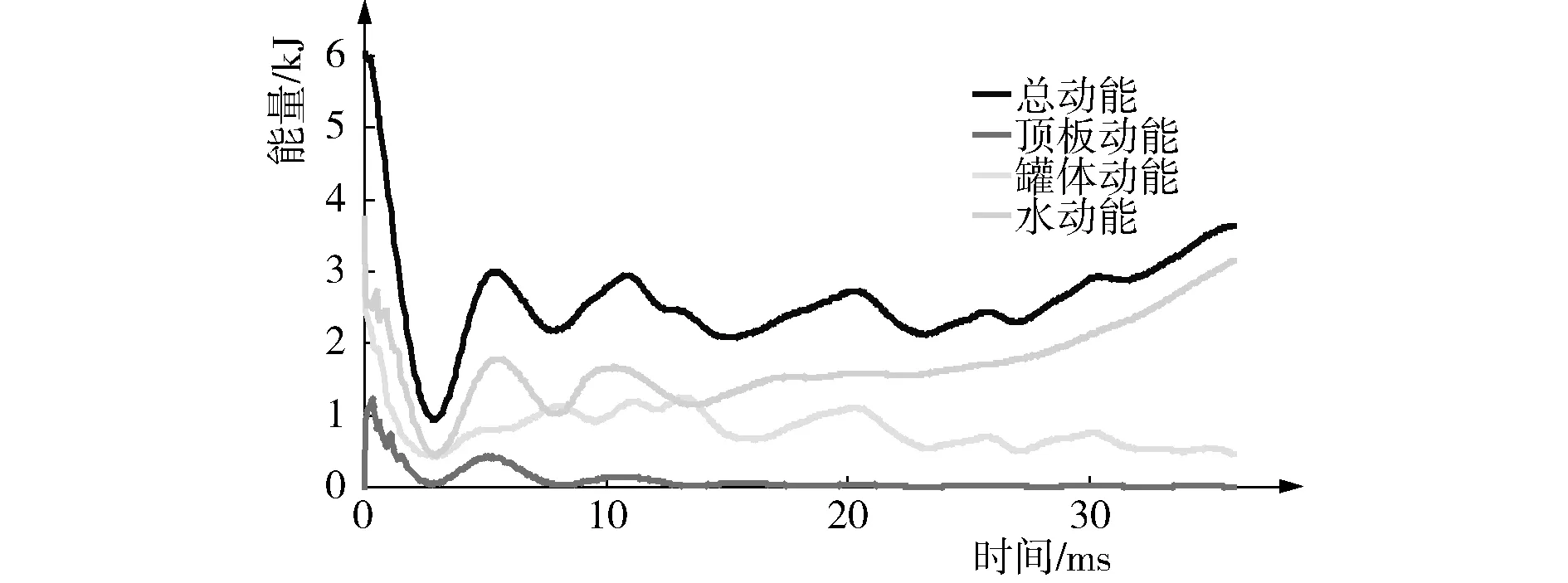
图3 动能随时间的变化
内能由弹性应变能和塑性应变能力两部分组成。弹性和塑性应变能力随时间的变化如图4和图5所示。在图4中,顶板的弹性应变能在前15 ms内波动较大,并迅速减小至一个较小值。罐体的应变能则基本保持在1 kJ左右,因此,弹性应变能仅是变形获得总内能的很小一部分。图5表明,与弹性应变能力相比,塑性应变能的数值较大,整体的塑性应变能力一直持续增加至3 kJ。在10 ms之前,顶板的塑性应变能迅速增加至1.8 kJ并保持稳定;罐体的塑性应变能则持续增加至1.2 kJ。

图4 弹性能随时间的变化
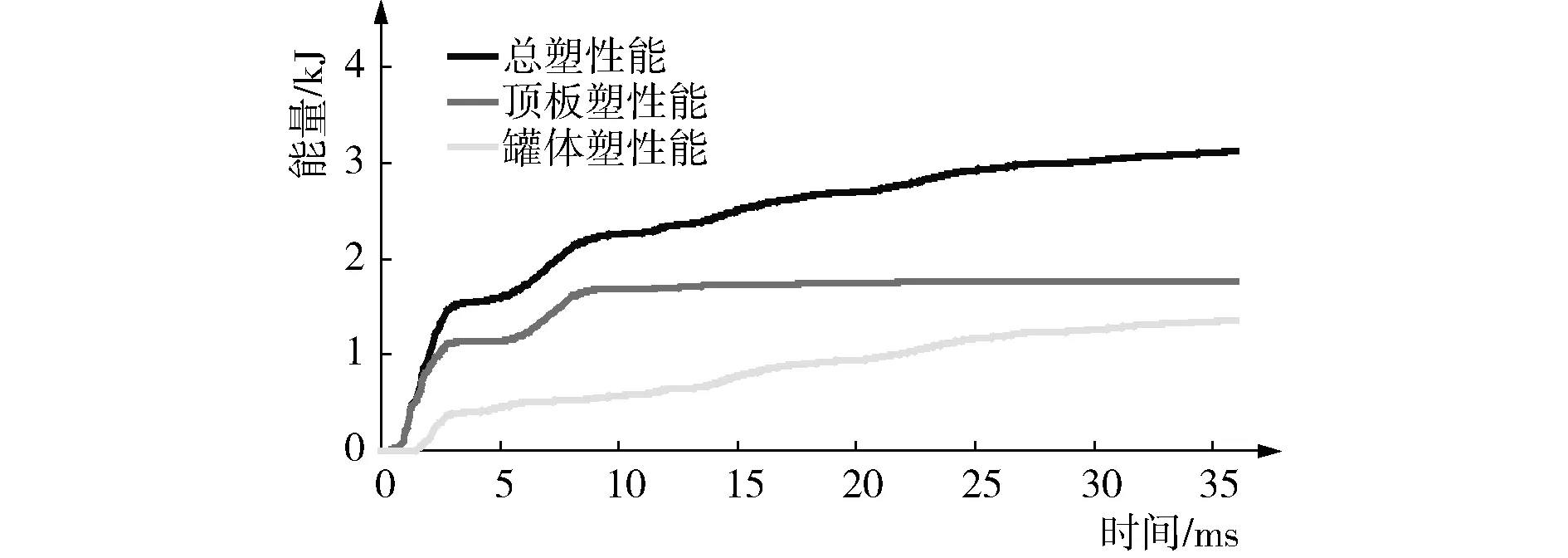
图5 塑性能随时间的变化
碰撞后的水位变化可以通过欧拉单元的分布来描述,如图6所示。由图6可知,碰撞后水的中心上升,临近罐体四周的水与壁面分离,随后顶部水位随时间往外扩展。此现象与其他跌落、碰撞试验、模拟结果相似[9-10]。因此,罐体内的水起到了将动能传递的作用,这对能量耗散是有利的。

图6 水位随时间的变化
根据以上描述,内能主要来自结构的塑性变形。顶板和罐体结构的等效塑性应变分布如图7和图8所示。由图可知,顶板和罐体较大的塑性应变发生在接触区域,最大的顶板塑性应变为1.83%,罐体塑性应变为0.93%,远小于极限值,因而结构能够承受碰撞变形而不会引发断裂。

图7 顶板结构等效塑性应变分布

图8 罐体结构等效塑性应变分布
顶板的支撑反力随时间的变化如图9所示。由图可知,最大的反力发生在碰撞方向Z,其他两个方向的反力较小。Z向反力的最大值达到了1 200 kN,发生在3 ms左右,并以三角函数波形变化和衰减,波动周期在12 ms左右。

图9 反力随时间的变化
4 结论
采用耦合的欧拉-拉格朗日方法进行了水下结构物和储水罐体的碰撞模拟分析。其中水采用欧拉单元模拟,从而适应其大变形特性。碰撞前的速度和动能采用相关规范中的推荐方法计算,材料属性也基于规范选取,有限元模型考虑了碰撞力所造成的渐进破坏。
模拟结果包括碰撞过程的能量变化和结构破坏评估。根据分析可知,动能大部分转化为结构内能和水动能,结构物的动能较小。最终的罐体和顶板的内能相当,主要的内能来自于结构的塑性变形。结果还包括不同时间下的水位变化,并与文献中空气中自由跌落试验和模拟结论类似,从一定程度上验证了有限元模型设置的正确性。碰撞以后的塑性应变分布表明,顶板和罐体结构均没有大的破坏而断裂。顶板的反力随着时间按照三角函数形状变化,并逐渐衰减。

