含能材料三种生成热计算方法的比较

刘 玥,易平平,林晨晨,刘 超,易小艺,何 飘

(中南大学 化学化工学院,湖南 长沙 410083)

引 言

含能材料的生成热是评价爆轰性能与稳定性的重要参数,其中,固相生成热是计算爆速(D)和爆压(P)必不可少的数据[1-3]。对于一般化合物,可通过查阅官方网站(如NIST网站)及热力学手册获得生成热数据,或是先测定燃烧热再进行计算。但是对于含能材料而言,由于其高能量特性,它们的生成热往往难以实测。因此,采用理论方法高效精确地计算其生成热,是研究含能材料性质的重要方法,也是影响预测爆轰性能准确性的一大关键因素,备受实验和理论科学家的关注。

随着计算机技术的发展,应用理论计算准确地预测小分子的生成热已经成为一种方便易行的方法[4-8]。计算化学主要的理论方法有:量子力学、分子力学、统计动力学和分子力学以及以上方法的组合[9]。量子化学是用量子力学的原理研究原子、分子和晶体的电子层结构、化学键理论、分子间作用力、化学反应理论、各种光谱、波谱和电子能谱的理论以及无机和有机化合物、生物大分子和各种功能材料的结构和性能关系的科学[10]。量子化学理论方法可分为从头算方法( ab initio )[11]、半经验分子轨道法[12]和密度泛函理论( DFT )方法[13]。从头算法一般比较耗时,需要大量的内存和磁盘空间[11];半经验分子轨道法比第一性原理计算快很多,可是如果计算的分子与参数化时使用的分子结构不相近,半经验方法可能给出完全错误的结果[12]。而DFT方法则具有明显的优势,它可以直接确定精确的基态能量和电子密度[14],用电子密度取代波函数作为研究的基本量,大大简化了电子结构的计算,并且可以较为准确地预测分子的几何构型及热化学性质[13]。

用量子化学方法计算生成热的一大难点是计算结果不直接提供生成热,只给出分子的总能量与热力学焓值等数据,需借助辅助反应才能求得化合物的生成热。常用的辅助反应包括原子化能反应法[15]、原子当量反应法[16]、等键反应法[17]。运用等键反应进行误差抵消,虽然可以大大减少计算量,但是由于方法构造的不确定,将导致同一等级计算结果的不确定。运用原子化能法可以直接计算分子的生成热,对于给定的计算方法,计算结果相对固定;但是为了得到准确的数值,往往需要非常高等级的计算方法和计算资源。自1989年John Pople[18]等发表Gaussian-1(简称G1)以来,已经有G2、G3和G4等四代方法。高斯理论方法(Gaussian theory)是迄今为止最为广泛使用的计算化合物能量的方法之一,在缺少实验值的情况下,其计算结果也被当作标准数值使用,然而高精度方法如G4对于多分子体系而言耗时太过昂贵。2011年,Bun Chan 等[19]提出了G4(MP2)-6X热力学组合方法,该方法相对于G4(MP2)最主要变化,是把CCSD(T)的CCSD和(T)部分的相关能进行系数校正,并把MP2换成了SCS-MP2,而且给出了可直接输出H(0)和H(T)数值的脚本,耗时与G4(MP2)相当,而精度接近G4。

本研究设计了160种新型含能分子,并在B3LYP/6-311G(d, p)//MP2/6-311++G(d, p)下用3种辅助反应(原子化能方法、等键反应方法与原子当量方法)计算标准摩尔生成热值,与G4(MP2)-6X方法结合原子化能方法计算的标准摩尔生成热值做相关性分析,并对4种方法进行了比较研究。

1 计算方法

运用Gaussion 09[20]软件,在B3YLP/6-311G( d, p)理论水平下,对设计的160个含能分子进行几何优化,并进行振动频率计算,获得零点振动能ZPE,所得结构均证实为势能面上的极小点(无虚频);在MP2/6-311++G(d, p) 理论水平下获得更精确的电子能E(MP2),在此基础上分别借助原子化能反应、原子当量反应、等键反应求得化合物的生成热。同时,将G4(MP2)-6X方法中的几何优化与振动频率计算的泛函与基组采用B3LYP/6-311G( d, p)以节约计算资源,并在Bun Chan[19]给出的脚本文件中做出了修改以直接输出298K下的焓值H(298K),结合原子化能方法计算得到化合物的气相生成热。

原子化能方法(Atomization Energies)[15],首先分别计算同一等级下分子与组成原子的焓值,并利用NIST网站[21]查得孤立原子的生成热,通过计算原子化能反应能来预测分子的气相生成热。计算公式如下:

ΔfHm(298K,M)=∑νiΔfHm(Atom,298K)-
[∑νiH(Atom,298K)-H(M,298K)]

(1)

ΔfHm(298K,M)=ΔfHm(0K,M)+
[Hcorr(M)-∑viHcorr(Atom)]

(2)

ΔfHm(0K,M)=∑νiΔfHm(0K,Atom)-ΔrHm(0K)

(3)

ΔrHm(0K)=∑νiE0(Atom)-E0(M)

(4)

式中:H(M,298K)为298K分子的焓值;∑νiH(Atom,298K)为298K的焓值;∑νiΔfHm(Atom,298K)为298K原子的标准生成热;E0是电子能与零点能之和;Hcorr是分子从0K到298K的热力学矫正值,孤立原子C、H、O、N的ΔfHm,0K实验值可由NIST网站[21]查得。

原子当量反应法(Atom Equivalent)[16]与原子化能相似,都是利用量子化学方法计算由分子形成原子时的能量变化,并且结合已知原子的相关信息,从而预测分子的生成热。原子当量方法计算公式如下:

ΔHi=Ei-∑jnjεj

(5)

式中:Ei是分子i的能量;εj记作一个“原子当量”,定义为εj=(Ej-xj),其中Ej是原子j的能量;nj是分子i中原子j的数目;xj是对原子j的理论水平校正。

等键反应法(Isodesmic Reaction)[17]是计算化合物生成热的一种较为精确的方法。在设计的等键反应体系中,化学键的类型和数目相同,产物分子和反应物分子电子环境相似,故电子相关造成的误差可以相互抵消,使得计算生成热的误差大大降低。等键反应方法基于Hess定律[22],通过设计等键反应,计算参与等键反应的分子的电子能量(E0)、零点振动能(ZPE)、热校正值(HT),利用下列等式计算等键反应的焓变ΔH298,由NIST网站[21]查的参考物质在标准状态下的生成热值,通过式(6)～(10)计算得到目标分子的气态生成热。

(6)

ΔE0=∑E0,P-∑E0,R

(7)

ΔZPE=∑ZPEP-∑ZPER

(8)

ΔHT=∑HT,P-∑HT,R

(9)

ΔH298=ΔE0+ΔZPE+ΔHT

(10)

2 结果与讨论

本研究以1,2,3-三唑和1,2,4-三唑为基础,唑环N1引入羟基,由H、—N═N—、—NH—NH—、—NH—、—CH2—、四嗪、吡唑和呋咱连接成双环三唑,设计16种桥连三唑-N-氧化物分子骨架类型,通过—CH3、—NH2、—OH、—CN、—NO2、—NHNO2、—NHNH2、—C(NO2)2、—C(NO2)3等基团调节能量和稳定性,获得160种新型含能分子结构式如图1所示。

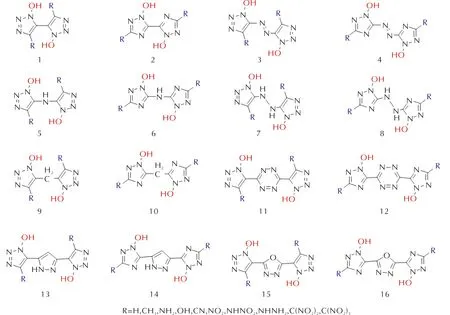
图1 设计的16种桥连三唑分子骨架类型Fig.1 Designed 16 kinds of molecular framework types of pontotriazole

2.1 几何优化

为了选取合适的计算模型,本研究中160个分子的初始结构都设置为能量更低的反式构象(反式1,2,3-三唑、反式1,2,4-三唑)。几何优化收敛后,桥基为H(1)、—N═N—(2)、四嗪(6)、吡唑(7)、呋咱(8)的化合物,环骨架仍保持和初始结构相似的平面构型,而其他桥连化合物(桥基为—NH—、—NHNH—、—CH2—),在桥基处有“折角”,使得两个唑环无法共平面。

由吡唑(7)、呋咱(8)桥接的双环三唑化合物,均翻转为顺式构型,说明由这两种桥基连接的化合物更趋于顺式构象;而由H(1)、—N═N—(2)、—NH—(3)、—NHNH—(4)、—CH2—(5)、四嗪(6)连接的双环三唑化合物趋于反式构象。本研究的160个分子的几何优化结构图见支撑材料中图S1～S9,图2为—H取代基系列的几何优化构型图。

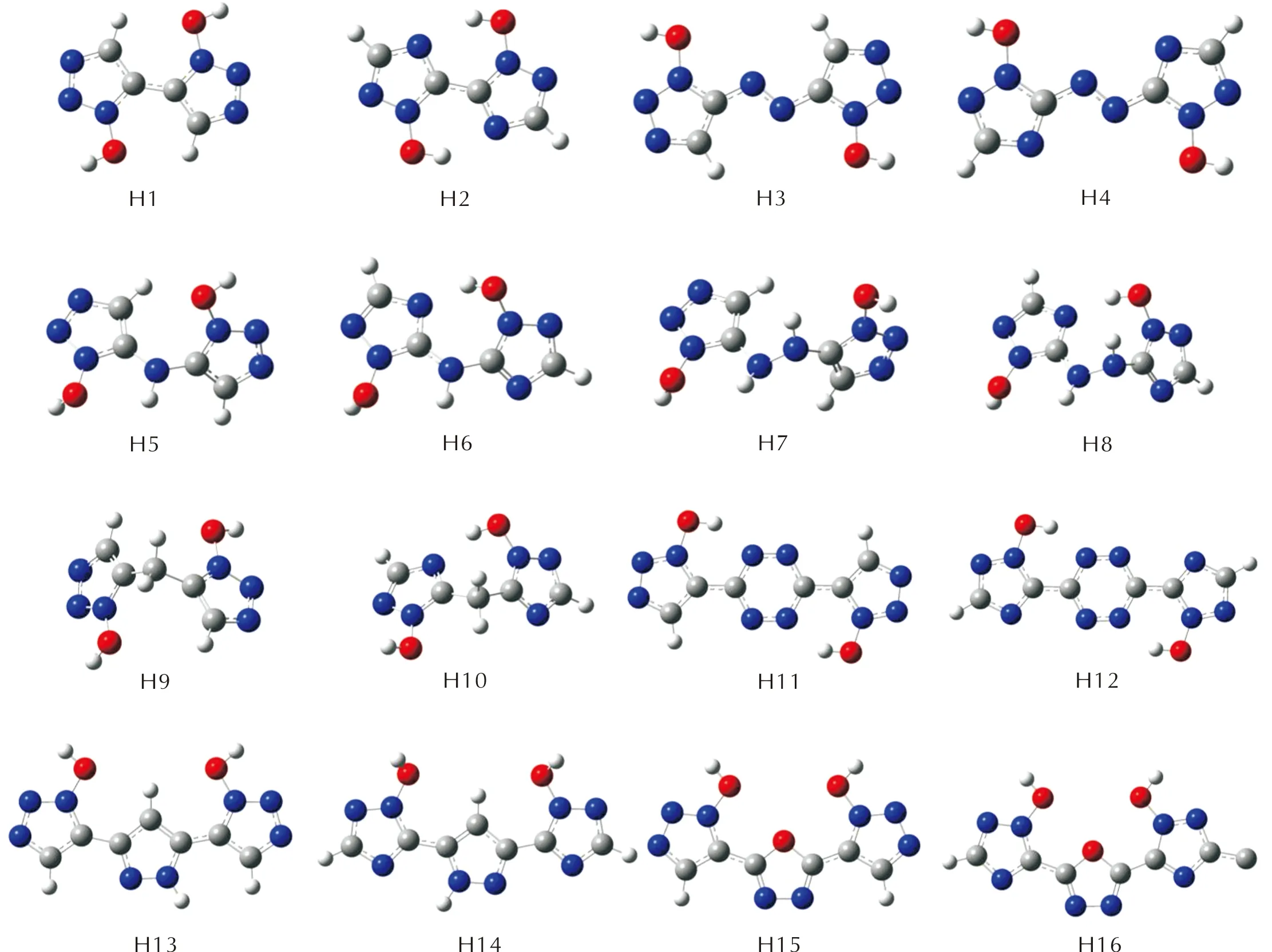
图2 —H取代基系列的结构优化构型图Fig.2 Optimized configurations of H series

以H(1)、—N═N—(2)、四嗪(6)、吡唑(7)、呋咱(8)为桥基的桥连双环三唑环,环骨架仍保持和初始结构相似的平面构型,表明当唑环与桥基共轭共平面时,分子的稳定性更高;此外,—N═N—、四嗪、吡唑、呋咱这类桥基,由于体系中引入了N—C、N—N键,将有利于提高含能化合物的爆炸性质[23]。而—NH—(3)、—NHNH—(4)、—CH2—(5) 桥连化合物中,两个唑环面存在“折角”,两个唑环和桥基之间由于电子排斥作用而呈异面构型。这可能是因为—NH—与—NHNH—的孤对电子在sp3杂化轨道,无法与唑环的游离电子共轭,而—CH2—没有多余的孤对电子或空轨道;这三种桥基的H原子处在sp3杂化轨道,受空间排斥的影响,两个唑环与桥基均呈异面构型。

由吡唑(7)、呋咱(8)桥接的双环三唑化合物均翻转为了顺式构型,说明由这两种桥基连接的化合物更趋于顺式构象;这可能因为反式构型下,吡唑上的H与唑环羟基上的O的距离为1.55605Å,相比于顺式构型下吡唑H与羟基O的距离为2.47471Å,原子间空间斥力更弱;呋咱系列化合物在顺式构型下取代基对称向两边伸展,而反式构型下取代基受呋咱的空间排斥。

2.2 不同方法计算的生成热对比

用G4MP2-6X方法计算了常用炸药TNT、NTO、FOX-7、TATB与LLM-105的固态生成热,结果见表1。与NIST网站查阅的实验值对比,误差不超过40kJ /mol,证明G4MP2-6X方法预测的标准生成热结果可信。

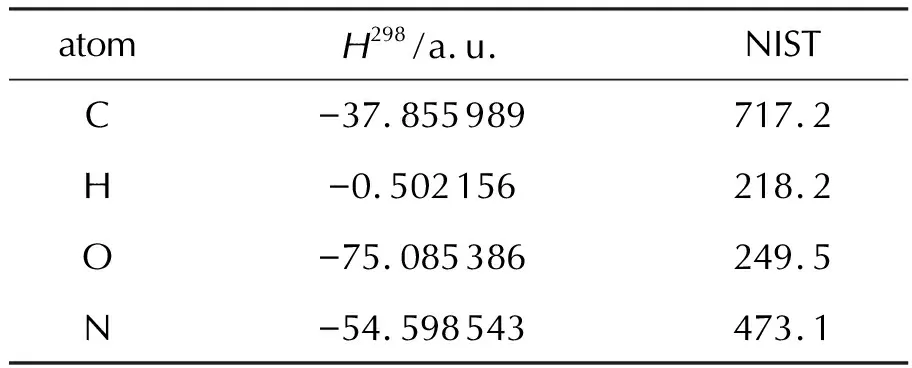
表1 C, H, O, N原子的计算焓值和实验焓值Table 1 Enthalpies for atoms C, H, N and O and their literature values for atomic ΔH°f,298/(kJ/mol)

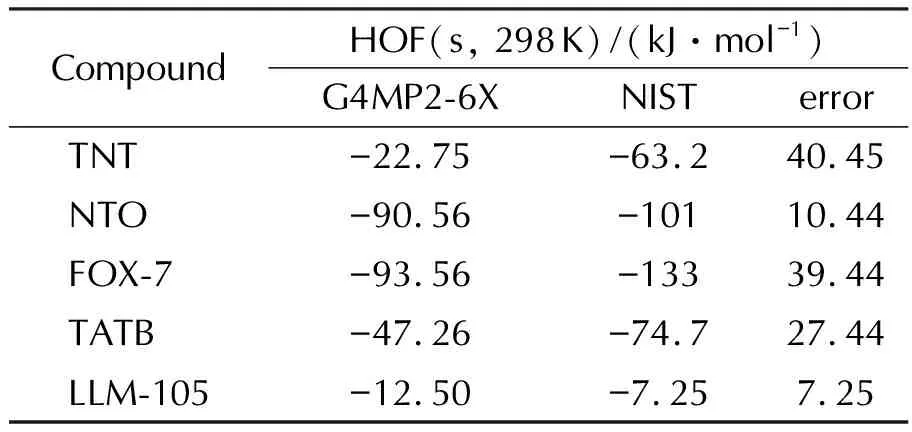
表1 G4MP2-6X计算方法得到传统含能化合物的HOF(s, 298K)值及与NIST实验值对比Table 1 Comparison of the HOF(s, 298K) values calculated by G4MP2-6X and experimental values by NIST

在B3LYP/6-311G(d,p)//MP2/6-311++G(d,p)理论水平下,分别用原子化能法、原子当量法与等键反应法对160种设计的含能分子的标准摩尔生成热进行计算,并与G4MP2-6X方法直接读取的标准摩尔生成热值进行对比,结果如表2所示。

表2 C、H、O、N原子当量Table 2 Atom equivalents of C, H, N and O

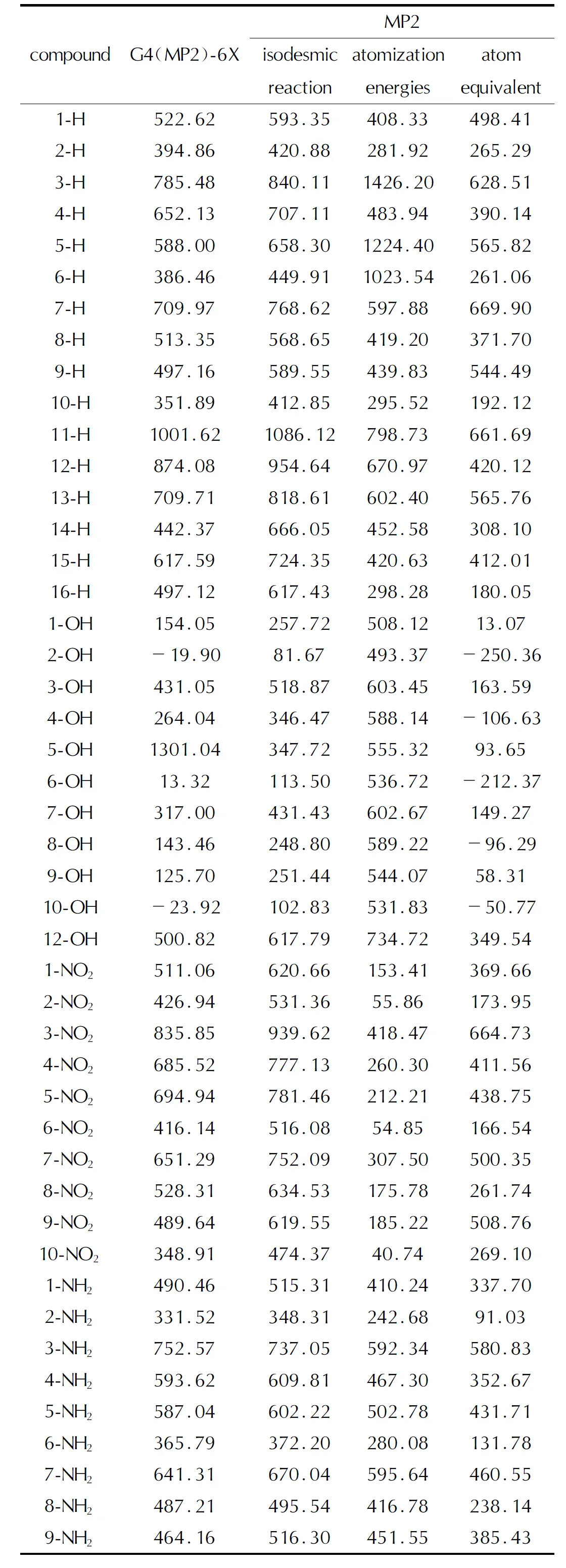
表2 不同方法计算的HOF(g, 298K)值Table 2 The HOF(g, 298K) values calculated by different methods

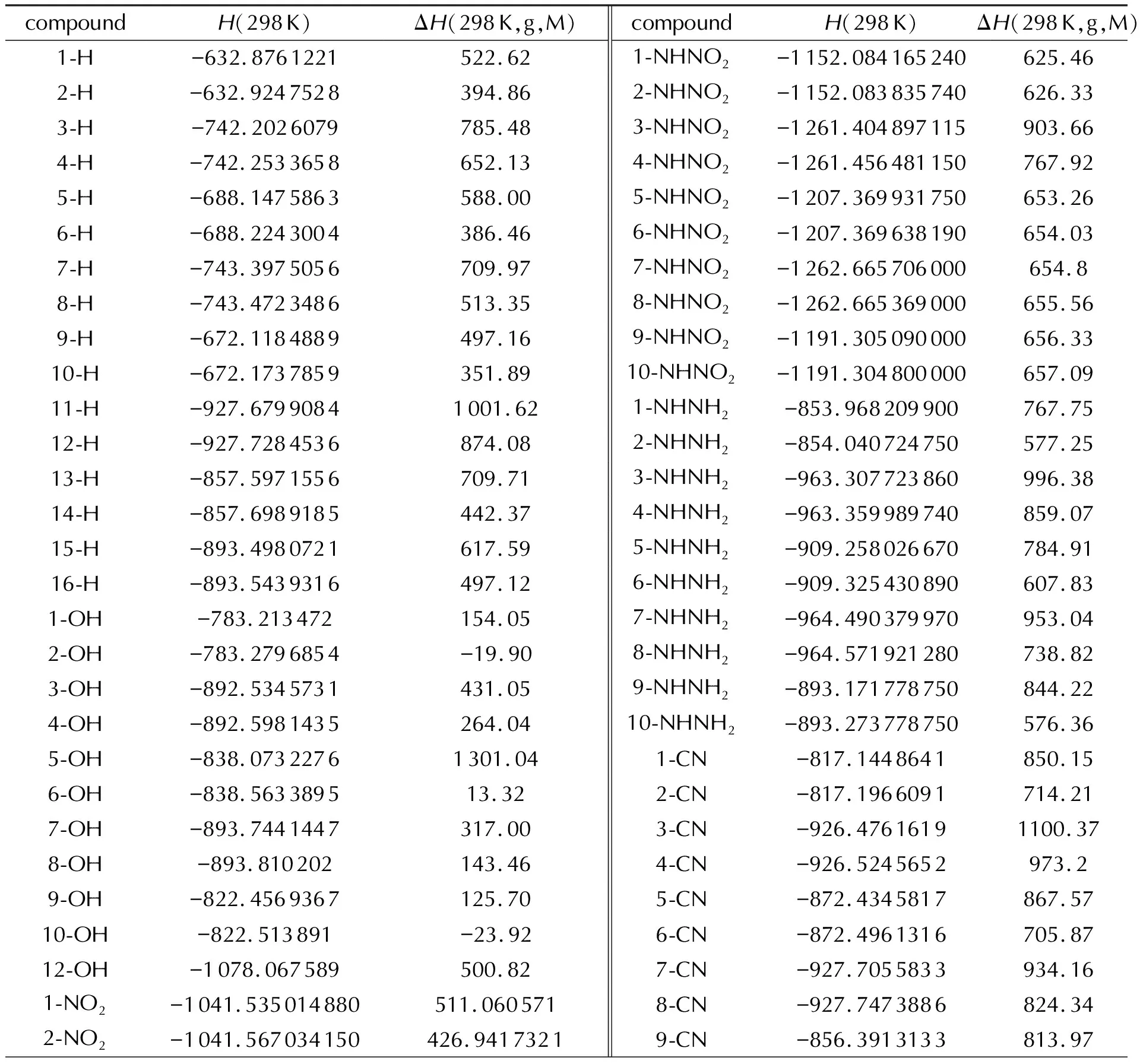
表3 G4(MP2)-6X方法结合原子化能方法的计算数据Table 3 Calculation data of G4(MP2)-6X method combing the Atomization energies method

为了对比3种辅助反应(原子化能方法、等键反应方法与原子当量方法)求得的标准摩尔生成热与G4(MP2)-6X方法结合原子化能方法输出的标准摩尔生成热的相关性,分别绘制了3种方法与G4(MP2)-6X方法的线性相关图,并拟合了辅助方法与G4(MP2)-6X方法的生成热的一元回归方程,如图3所示。其中,原子化能方法的相关性最高,相关系数为0.88513;等键反应方法次之,相关系数为0.43492;原子当量方法的相关性最低,仅有0.15977。对于本研究的160个含能分子,等键反应的相关性较低,可能是因为以—H(1)、—N═N—(2)、四嗪(6)、吡唑(7)、呋咱(8)为连接基团的分子,它们的共轭环骨架在等键拆分时被破坏,并且无法利用已有气相实验生成热数据的小分子建立等键方程以还原共轭的电子环境,从而带来误差。

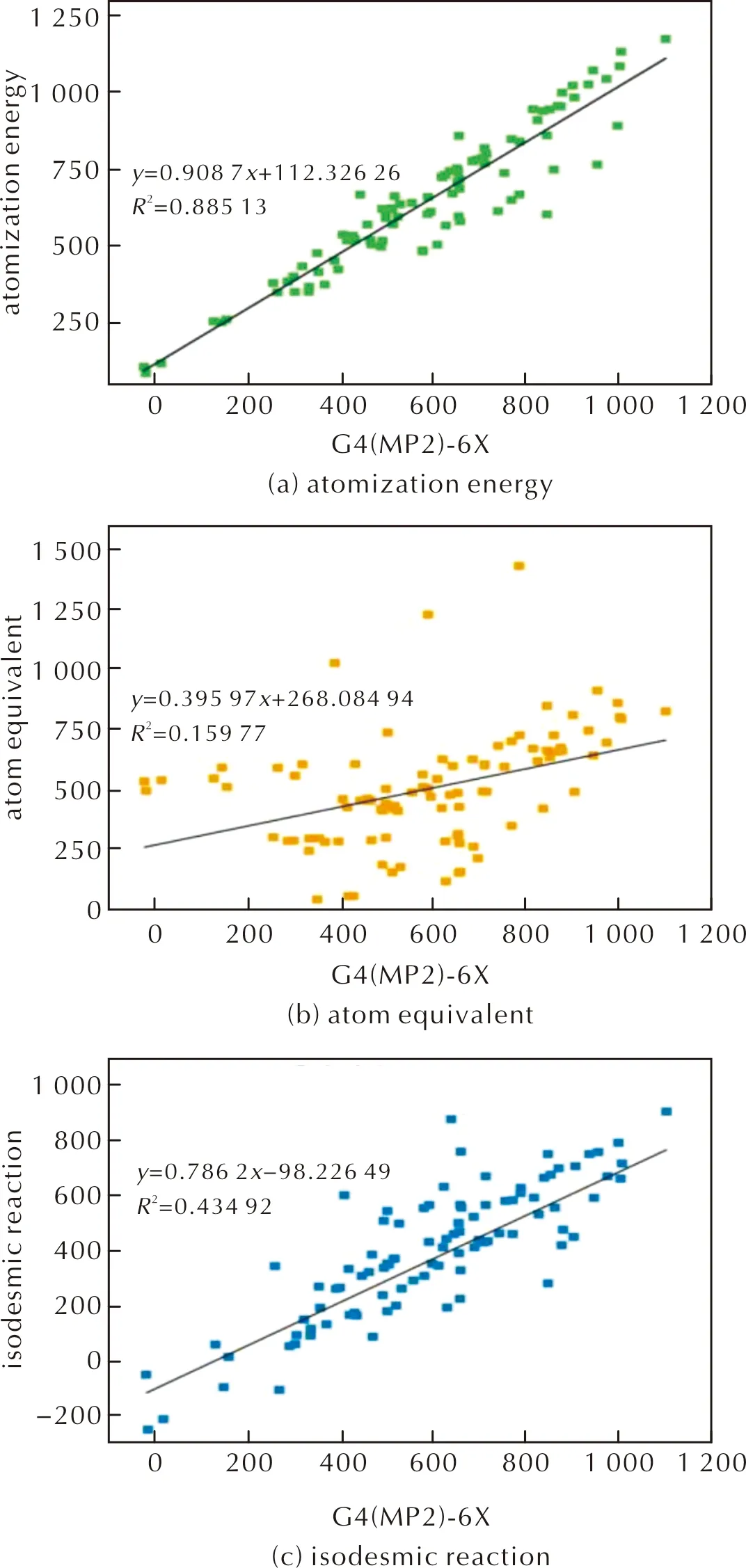
图3 不同方法所计算的HOF值与G4(MP2)-6X方法输出的HOF值的拟合曲线图Fig.3 Fitting curves of HOF values calculated by different methods with the values by G4(MP2)-6X methods

图4为按照基团分类的160个化合物的HOF值(原子化能方法计算)。

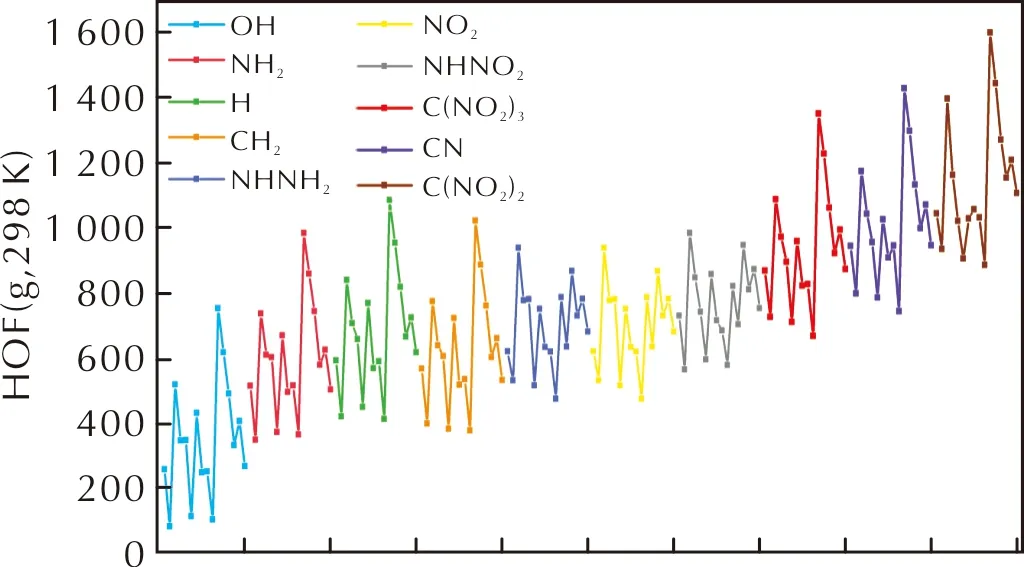
图4 原子化能方法计算的160个化合物的HOF(g,298K)值Fig.4 HOF(g,298K) values of 160 kinds of compounds calculated by atomization energy

由图4可知,取代基—C(NO2)2、—C(NO2)3、—NHNO2和—CN显著提高了分子的生成热,而—OH与—NH2取代基系列的生成热低于—H系列。—C(NO2)2的氮含量与CN键数量都不如—C(NO2)3,但HOF值更高,这可能因为偕二硝基基团呈平面构型,共轭的结构使得生成热提高。同一桥基连接的联三唑同分异构体(联1,2,3-三唑,联1,2,4-三唑),桥连双1,2,3-三唑的HOF更大,这可能因为1,2,3-三唑的生成焓(272kJ mol-1)比1,2,4-三唑(109kJ mol-1)高。对于10种不同取代基,四嗪联三唑分子骨架都具有最高的HOF值,可能因为四嗪与三唑环共轭,分子生成热提高。

3 结 论

(1)探究了目前常用3种辅助方法计算的HOF值与G4(MP2)-6X方法结合原子化能方法输出HOF值的相关性。首先在B3LYP/6-311G(d, p)理论水平下对160种新型含能分子进行结构优化、频率计算,并进一步在更高级别的MP2/6-311++G(d, p)理论水平下对分子进行了单点能计算。分别读取热力学数值与电子能量,利用3种常用的辅助反应(原子化能方法、等键反应方法和原子当量方法)计算HOF值,对比G4(MP2)-6X方法输出的HOF值,并拟合了与G4(MP2)-6X方法的相关性。

(2)3种方法的相关性为:原子化能方法(0.88513)>等键反应方法( 0.43492 )>原子当量方法(0.15977)。建立了线性回归方程,可采用该方程结合B3LYP/6-311G(d, p)//MP2/6-311++G(d, p)理论水平获得G4(MP2)-6X方法的计算精度。本研究计算的160个物质在不同理论水平和生成焓计算方法下的生成焓,可供广大研究人员参考使用。

图S1 —CH3取代基系列分子的几何优化构型图Fig.S1 Optimized configurations of —CH3 series

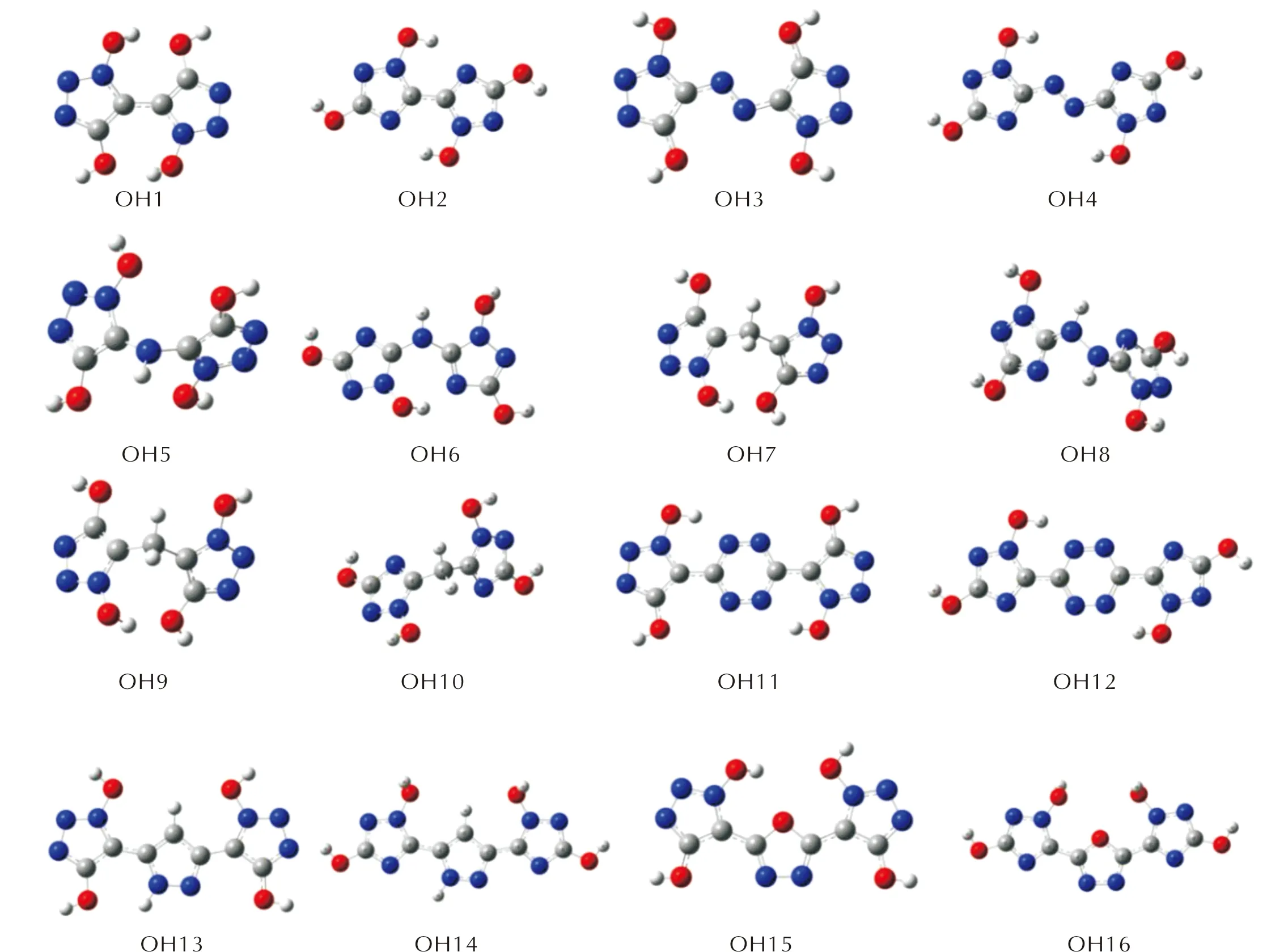
图S2 —OH取代基系列分子的几何优化构型图Fig.S2 Optimized configurations of —OH series

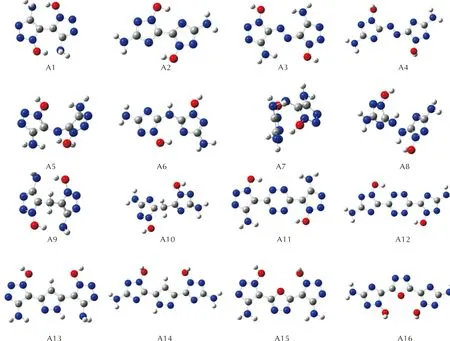
图S3 —NH2取代基系列分子的几何优化构型图Fig.S3 Optimized configurations of —NH2 series

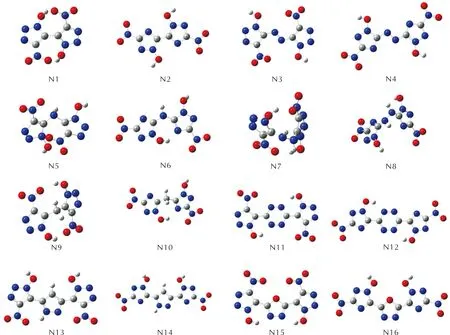
图S4 —CN取代基系列分子的几何优化构型图Fig.S4 Optimized configurations of —CN series

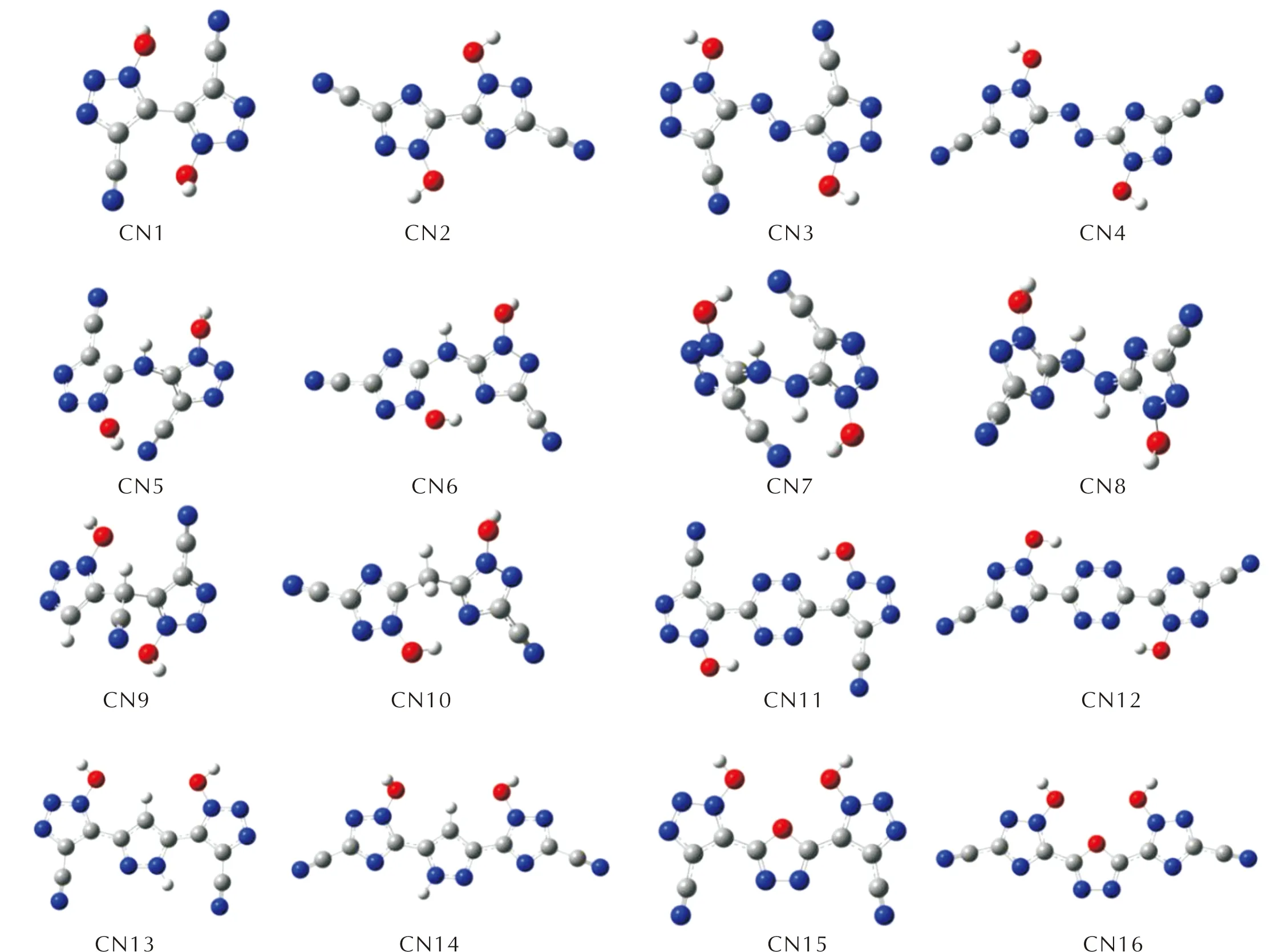
图S5 —NO2取代基系列分子的几何优化构型图Fig.S5 Optimized configurations of —NO2 series

(相关支撑材料见文后)

支撑材料

1 计算方法

原子化能方法使用的原子焓值如表1所示。

原子当量反应法中使用如表2所示Rice[1]拟合的原子当量。

构建等键反应用到的分子包括1,2,4-三唑、1,2,3-三唑、NH3、N2H4、CH3NH2、N2H2、H2、C2H6、C2H4、CH3NHNH2、CH4、CH3OH、C2H5NOHC2H5、C2H5NHC2H5、CH3CH2CH3、C3H4N2、CH3OCH3、CH3CN、CH3NO2、CH3NHCH3、C2H5OC2H5, 在B3LYP/6-311G(d, p)//MP2/6-311++G(d, p)水平进行几何优化、振动频率与单点能计算,由NIST网站[2]查得标况下的生成焓值。

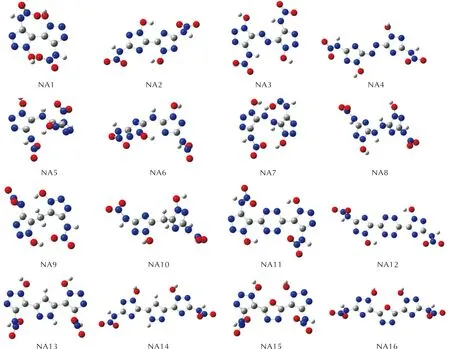
图S6 —NHNO2取代基系列分子的几何优化构型图Fig.S6 Optimized configurations of —NHNO2 series

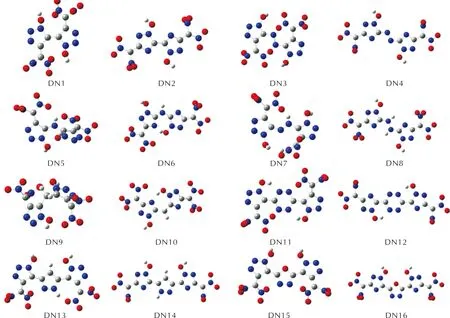
图S8 —C(NO2)2取代基系列分子的几何优化构型图Fig.S8 Optimized configurations of —C(NO2)2 series

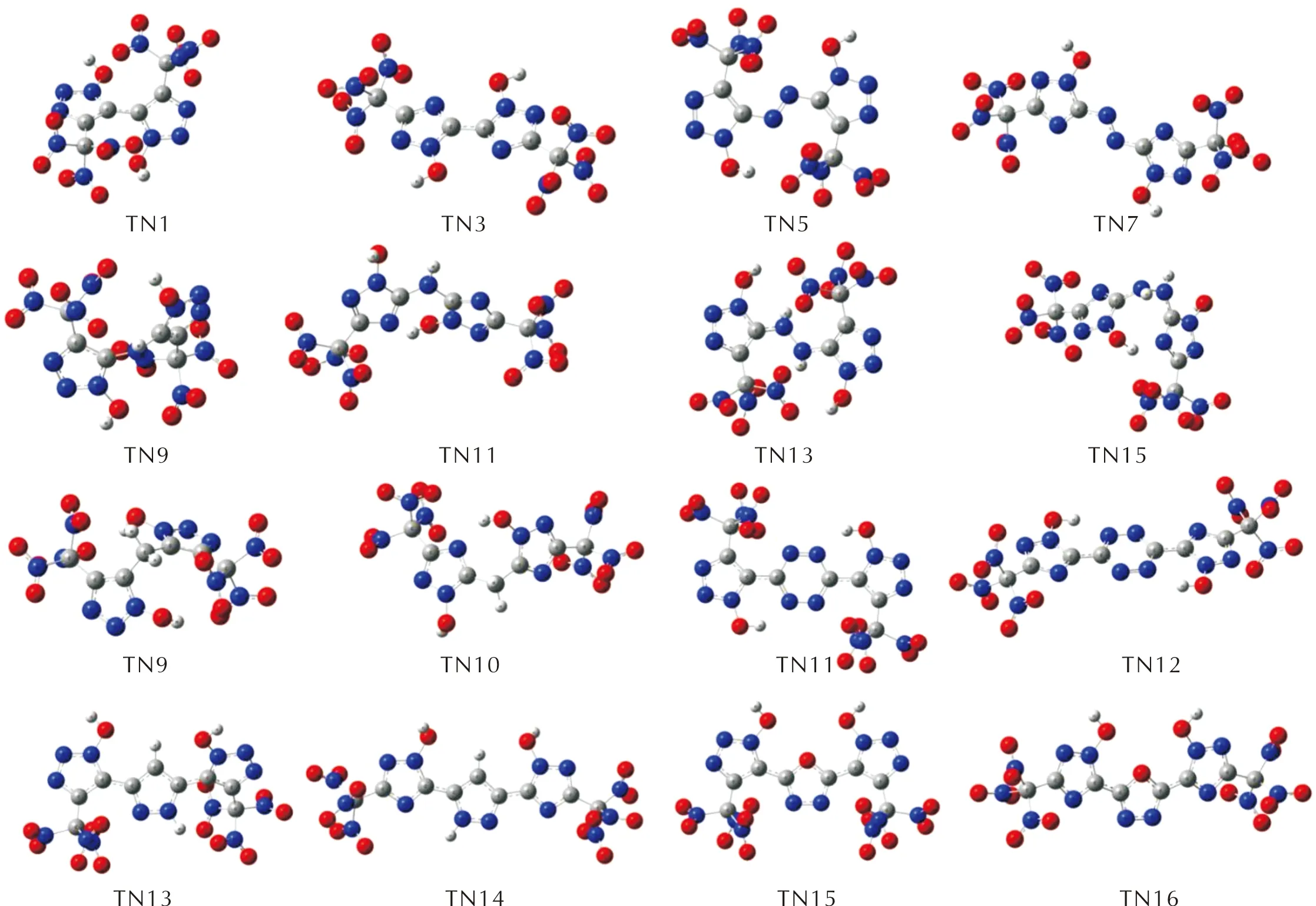
图S9 —C(NO2)3取代基系列分子的几何优化构型图Fig.S9 Optimized configurations of —C(NO2)3 series

2 几何优化构型图