基于HHO-CNN的轴承故障诊断方法研究

刘玉鑫,武文博,张雄,万书亭

(1.国家电投内蒙古能源有限公司 通辽霍林河坑口发电有限责任公司,内蒙古 通辽 028000;2.华北电力大学 机械工程系,河北 保定 071003)

轴承被称作是旋转机械的关节,广泛应用于带式输送机托辊群、风力发电机传动链等设备中,起到重要的支撑和传动作用.轴承的运行状态关乎整个机械设备的可靠性和稳定性,因此轴承的状态监测与故障诊断一直是本领域的热点问题.基于频域分析、时域分析和统计特征提取的诊断方法是常用的手段[1-2],这些方法具有明确的机理依据和良好的可解释性,但是传统特征提取方法往往依赖于领域专家的经验,且对于复杂多故障模式难以进行准确地识别.近年来,深度学习在众多领域迅猛发展,其强大的特征提取和学习能力在轴承故障诊断领域受到关注[3].机器学习模型,如卷积神经网络和递归神经网络(RNN),在处理复杂数据、挖掘数据隐藏的特征以及提高预测和诊断准确性方面表现出了卓越的能力.在轴承故障诊断中,机器学习模型可以从大量的监控数据中自主学习和识别故障模式,无需任何先验的知识或假设,极大地提高了故障诊断的效率和准确性[4-6].

尽管机器学习在轴承故障诊断中表现出了巨大的潜力,其应用仍面临着诸多困难.模型结构和参数选择、不均衡数据分布的权重匹配、模型决策过程的可解释性等问题仍待进一步解决.李昕燃等[7]提出了一种滚动轴承故障诊断方法,该方法以改进后的麻雀搜索算法(sparrow search algorithm,SSA)优化支持向量机(support vector machine,SVM),优化后的支持向量机能够实现更准确的自适应分类效果.杨昆等[8]提出了一种改进的Faster R-CNN目标检测和分类模型,该模型相比于优化前在运算性能和识别准确率等方面有显著提升.金岩磊等[9]结合灰狼算法和变分模态分解(variational mode decomposition,VMD)提出了改进的变分模态分解方法,并用于轴承故障信号分解及特征矩阵构建,利用卷积神经网络(convdutional neural network,CNN)模型对特征矩阵进行模式识别,达到了良好的诊断效果.金志浩等[10]将Welch功率谱和结合进行轴承的故障诊断,该方法具有很好的抗干扰能力.段洁利等[11]针对果园索道轴承提出了一维端对端轻量化CNN检测方法,该方法参数量小且准确率高,在有噪声的环境中有着很好的鲁棒性.针对CNN故障识别准确率和效率较低的问题,郑建波等[12]利用循环谱相关(CSCoh)提取轴承的故障特征,生成循环谱相关图像,应用CNN对生成的故障特征灰度图进行识别,从而实现轴承的故障诊断.

本文针对CNN处理多分类模式识别过程中由超参数问题引起的准确率低、收敛速度慢等问题,提出了一种基于哈里斯鹰优化(HHO)算法优化的CNN分类模型.使用HHO算法对CNN模型的超参数空间进行优化,计算适应度值并获取全连接层的单元数量和迭代次数,利用优化后的CNN模型对轴承数据集进行分类,通过实验数据集验证了所提方法的有效性.

1 理论依据

1.1 HHO算法

HHO算法是一种群智能优化算法,由Heidari等[13]于2019年提出,其灵感来源于哈里斯鹰独特且高效的捕猎策略.在此策略中,一群鹰会联手,从多个方向齐头并进地发动攻击,当其中一只表现最优秀的鹰做出冲击行动捕猎猎物时,其他的鹰会调整策略并接替其进行追击.这种策略转换在混淆逃逸的猎物方面效果显著.此战术的主要优势在于,哈里斯鹰能够不断地追逐猎物直至其筋疲力尽,最终由最强壮、经验最丰富的鹰轻松捕获并分享给同伴.HHO算法主要包含3个阶段:勘探、勘探与开发的转换以及开发阶段.

1.1.1 勘探阶段

HHO算法的种群初始化方法与大多数智能优化算法相同,即随机产生搜索空间中的若干候选解.设计2种策略模拟哈里斯鹰对猎物的搜索,并认为2种策略的采用概率是相等的(产生1个[0,1]的随机数和0.5进行比较).2种搜索策略如下:

(1)

(2)

(3)

其中,N代表种群规模.

1.1.2 从勘探到开发的转换阶段

HHO算法可以从勘探转换到开发,哈里斯鹰会根据猎物的逃跑能量,在勘探和开发行为之间进行转换.而猎物的能量在逃跑过程中是动态降低的,猎物的逃跑能量计算公式为

E=2E0(1-t/T),

(4)

其中,E0是猎物的初始逃跑能量,每次迭代中,在(-1,1)随机取值;T为最大迭代数.当E0在-1～0时,说明猎物身体衰弱;当E0在0～1时,说明猎物身体强壮.动态逃逸能量E在迭代过程中呈下降趋势.当逃逸能量|E|≥1时,鹰搜索不同的区域来探索猎物的位置,此时HHO算法处于勘探阶段;当|E|<1时,种群尝试在当前解的邻域内寻找更优解.总之,当|E|≥1时进行勘探,当|E|<1时进行开发.HHO算法在勘探和开发之间的动态转换如图1所示.

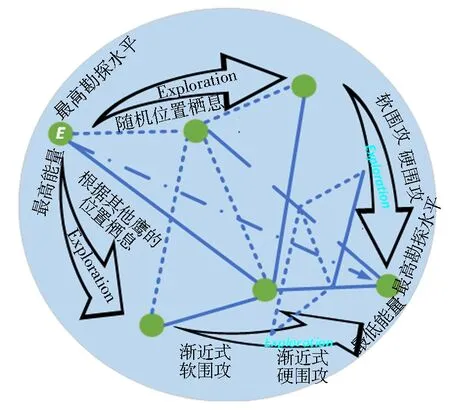
图1 猎物的逃跑能量转换Fig.1 Escape energy conversion plot of the prey

1.1.3 开发阶段

当|E|<1时,种群进入开发阶段.而在实际开发过程中,依据哈里斯鹰的捕食行为,设计了多种位置更新方式.首先定义一个[0,1]的随机数r.

软包围:当0.5≤|E|<1且r≥0.5时,哈里斯鹰采用软包围策略进行位置更新,

(5)

(6)

其中,J=2-2r,r是[0,1]随机数;即J是[0,2]的随机数;Δxt是当前最优个体的位置和当前个体之间的“距离”.

硬包围:当|E|<0.5且r≥0.5时,哈里斯鹰采用硬包围策略进行位置更新,

(7)

渐近快速俯冲的软包围:当0.5≤|E|<1且r<0.5时,猎物具有足够的能量逃脱追捕,因此在软包围下,哈里斯鹰需要进行突袭,即快速俯冲.在HHO算法中使用了Levy飞行模拟猎物的逃跑模式.假设哈里斯鹰可以在与同类的猎物竞争中选择较佳的俯冲方式扑向猎物.通过式(8)来帮助哈里斯鹰评估下一步的行动.

(8)

将这种评估与前一次的俯冲进行比较,以检测它是否是一次可行的俯冲,在接近猎物时做不规则的、突然且快速的俯冲.以Levy飞行来定义这种俯冲方式,

Z=Y+S·L(D),

(9)

S是一个D维随机向量,每个元素取值[0,1].L(x)代表Levy飞行函数,

(10)

其中,μ、v均为(0,1)的随机值;β是一个常数,设为1.5.将这种俯冲方式的选择设计为基于哈里斯鹰当前位置的适宜度,即

(11)

渐近快速俯冲的硬包围:当|E|<0.5且r<0.5时,猎物没有足够的能量逃跑,哈里斯鹰会进行硬包围,并进行俯冲以捕捉猎物.哈里斯鹰的下一步行为

(12)

如果哈里斯鹰发现猎物存在欺骗行为,也会改变其下一步行动,采用式(13)调整,

Z=Y+S·L(D)

(13)

1.2 CNN模型

在轴承故障诊断中,需要处理大量的振动信号数据,这些数据可以被看作是一维序列或者通过数学变换被转换为二维图像数据,CNN模型包括卷积层、池化层、展平层、全连接层和输出层,其中卷积层和池化层最为重要,CNN模型如图2所示.

图2 CNN模型Fig.2 CNN model

卷积层的作用是特征提取,卷积过程为

f=φ(W*x+b),

(14)

其中,x为振动信号数据,W卷积核矩阵,b为偏置量,φ为激活函数,*为卷积操作.

池化层用于减小特征图的尺寸,同时保留重要的信息.最常见的池化操作是最大池化,选择每个区域中的最大值,从而减小图像的空间分辨率,这有助于降低计算复杂度和防止过拟合.通常在卷积层之后应用激活函数,最常见的是修正线性单元(ReLU),以引入非线性性质,有助于CNN模型学习复杂的非线性关系.层叠结构,CNN通常由多个卷积层和池化层的层叠组成,以逐渐提取和组合不同级别的特征,这种层叠结构允许CNN学习图像的抽象表示.在CNN的顶部,通常有1个或多个全连接层,用于执行最终的分类或回归任务.这些层与前面的卷积和池化层之间的特征进行连接,并生成最终的预测结果.

CNN模型的一般执行过程包括数据采集、数据预处理、特征提取和分类、模型测试和评估等.通过振动传感器等设备收集轴承的运行数据,包括正常运行数据和不同故障状态下的数据,对原始的振动信号进行处理,可以直接将一维的振动信号作为输入,也可以通过时频分析等方法将其转化为二维的图像,比如使用短时傅里叶变换(STFT)、小波变换等,这样便于利用CNN在图像处理上的优势,使用CNN进行特征提取和分类.通过训练,CNN能够从数据中自动学习并提取出区分正常和故障轴承的特征,训练完成后,使用独立的测试集评估模型的性能,包括准确率、召回率、精确率等.相比于传统的全连接神经网络,CNN在处理轴承故障数据上,具有更好的性能和更高的效率,这主要得益于卷积操作和权重共享的设计,使得网络能够更好地捕捉轴承故障特征信息,并减少了大量的参数,从而降低了过拟合的风险.

2 模型参数

2.1 CNN模型参数设置

将CNN模型作为故障分类的主要模型,其中包含1层输入层、1层全连接层和1层输出层,模型的卷积层分别为1层、2层、3层时的准确率和损失率如图3所示,模型在卷积层为2层时损失率最低,而搭建卷积神经网络时,通常是在卷积层之后紧接着添加池化层.1层卷积层搭配1层池化层是一种常见的模式,有助于减小特征图的尺寸,减少计算负担,并逐渐提取特征,因此选取了2层卷积层、2层池化层构建CNN模型.设置CNN网络的具体参数如表1所示.在CNN网络模型中,卷积层使用ReLU激活函数,优化器为adam,交叉熵损失函数与分类任务的本质相符,易于优化和计算梯度,因此使用交叉熵损失函数作为目标函数来指导网络参数的学习,激活函数为Sigmoid.迭代次数初始设置为100,每次传递给模型的样本数量为16,其中训练集样本数量为90%,测试集为10%.

表1 CNN网络参数

2.2 HHO优化参数设置

HHO优化参数设置如表2所示.

表2 HHO初始化参数

使用HHO算法优化CNN模型的参数:首先,以损失函数最小化为优化的目标,将CNN模型的参数编码为一个可搜索的解空间;其次,使用HHO算法搜索最优解,在每一步迭代中,算法根据哈里斯鹰的捕食策略更新解,以期找到损失函数的最小值;最后,将算法找到的最优解解码回CNN模型的参数,并更新模型.

2.3 算法流程

实验流程如图4所示,实验的具体步骤如下.

步骤1:构建轴承故障数据集,其中训练集占90%,测试集占10%;

步骤2:初始CNN模型参数;

步骤3:利用HHO优化CNN,寻找最优迭代次数和全连接层单元数;

步骤4:捕获参数最优解并返回CNN模型,确定迭代次数和全连接层单元数;

步骤5:以Sigmoid作为激活函数,进行轴承故障分类;

步骤6:输出结果,将轴承分类的准确率和损失率转为图像输出.

3 实验信号处理

3.1 辛辛那提大学轴承实验台数据集

辛辛那提大学轴承实验台如图5所示,实验台由交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统和测试轴承等组成.采用高精度加速度计测量轴承X方向和Y方向的振动信号.实验采用Y方向上的振动信号构建数据集,采样频率为20 kHz,采样时长为1 s,采样点数为20 480.数据集标签设置为内圈故障、外圈故障、滚动体故障和正常数据.4类信号的时域如图6所示.

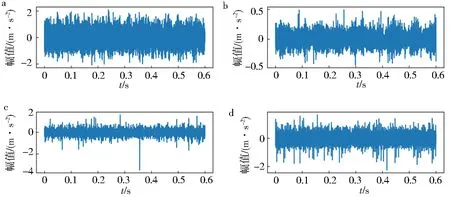
a.正常数据;b.内圈故障;c.外圈故障;d.滚动体故障图6 4类信号时域Fig.6 Time domain diagram of four types of signals

用CNN模型进行分类,得到的训练集和测试集的准确率和损失率如图7所示,准确率在迭代15次以后收敛,达到了96%.损失率在迭代100次以后还未收敛.

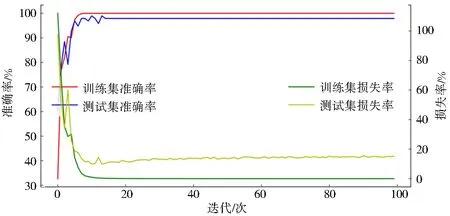
图7 4类信号CNN模型实验结果Fig.7 Experimental results of the CNN model for 4 types of signals

在优化算法中,适应度函数是用来评估解(即一组参数或决策变量)的质量.适应度值通常与解的好坏成正比:更好的解有更高的适应度值.利用HHO算法优化CNN,得到的优化参数见表3.

表3 HHO优化参数

将优化后的参数替代之前的预设参数,得到的模型准确率和损失率如图8所示,HHO-CNN模型准确率在迭代5次以后开始收敛,达到了100%的准确率,损失率在迭代50次以后开始收敛,损失率为0.较CNN模型在准确率和损失率都有了很大提升,同时在计算速度(FPS)和运行内存占用方面也有了很大进步,结果见表4.

表4 HHO-CNN和CNN内存占用和FPS对比

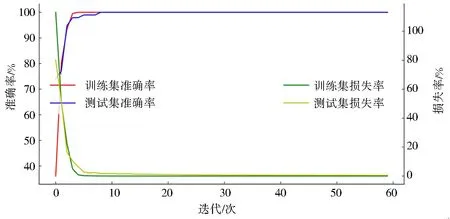
图8 4类信号HHO-CNN模型实验结果Fig.8 Experimental results of the HHO-CNN model for 4 types of signals

SNE是一种常见的无监督学习方法,用于降低数据集的维度,同时尽可能保留原始数据的变异性.T-SNE可以将高维的轴承数据可视化为二维的散点图,方便直观地理解轴承的故障分类.在图9中,HHO-CNN模型分类结果特别清晰,而CNN模型虽然已经成功分类,但是部分故障类型样本存在混叠.混淆矩阵显示了模型的真实标签和预测标签之间的关系,包括正确的预测(真阳性和真阴性)和错误的预测(假阳性和假阴性).通过混淆矩阵可以理解模型的性能,尤其是模型对于不同类别的分类情况,从而能够更准确地评估模型的精确度等指标.图9中,HHO-CNN模型没有分类错误,CNN模型存在2处分类错误.

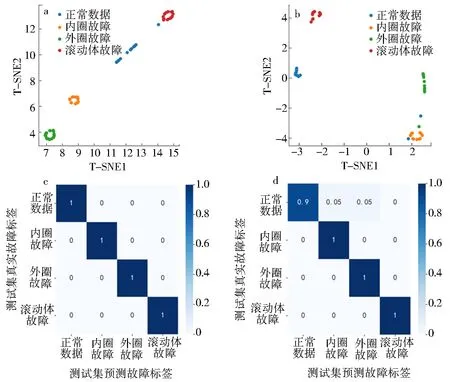
a.HHO-CNN降维可视化;b.CNN降维可视化;c.HHO-CNN混淆矩阵;d.CNN混淆矩阵图9 HHO-CNN和CNN模型实验结果对比Fig.9 Comparison of the experimental results of the HHO-CNN and CNN models

3.2 西安交通大学轴承数据

西安交通大学轴承实验平台由交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统和测试轴承等组成,如图10所示.实验中使用DT9837便携式动态信号采集器采集振动信号,以Y轴方向采集的信号构建数据集,采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s,采样点数为131 072,数据设置如表5所示.9种信号的时域见图11.

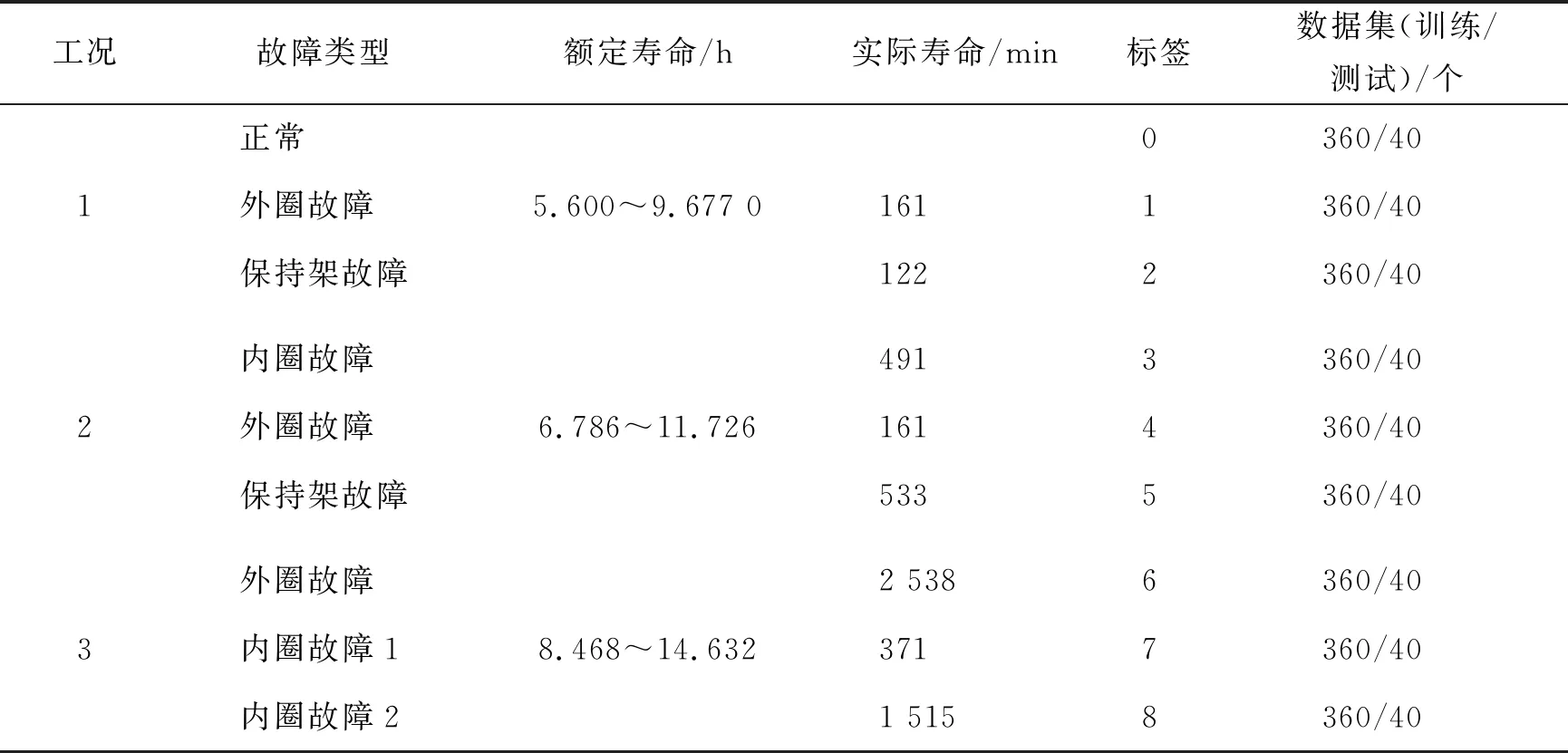
表5 数据设置

图10 西安交通大学轴承实验台Fig.10 Bearing experimental bench of Xi'an Jiaotong University

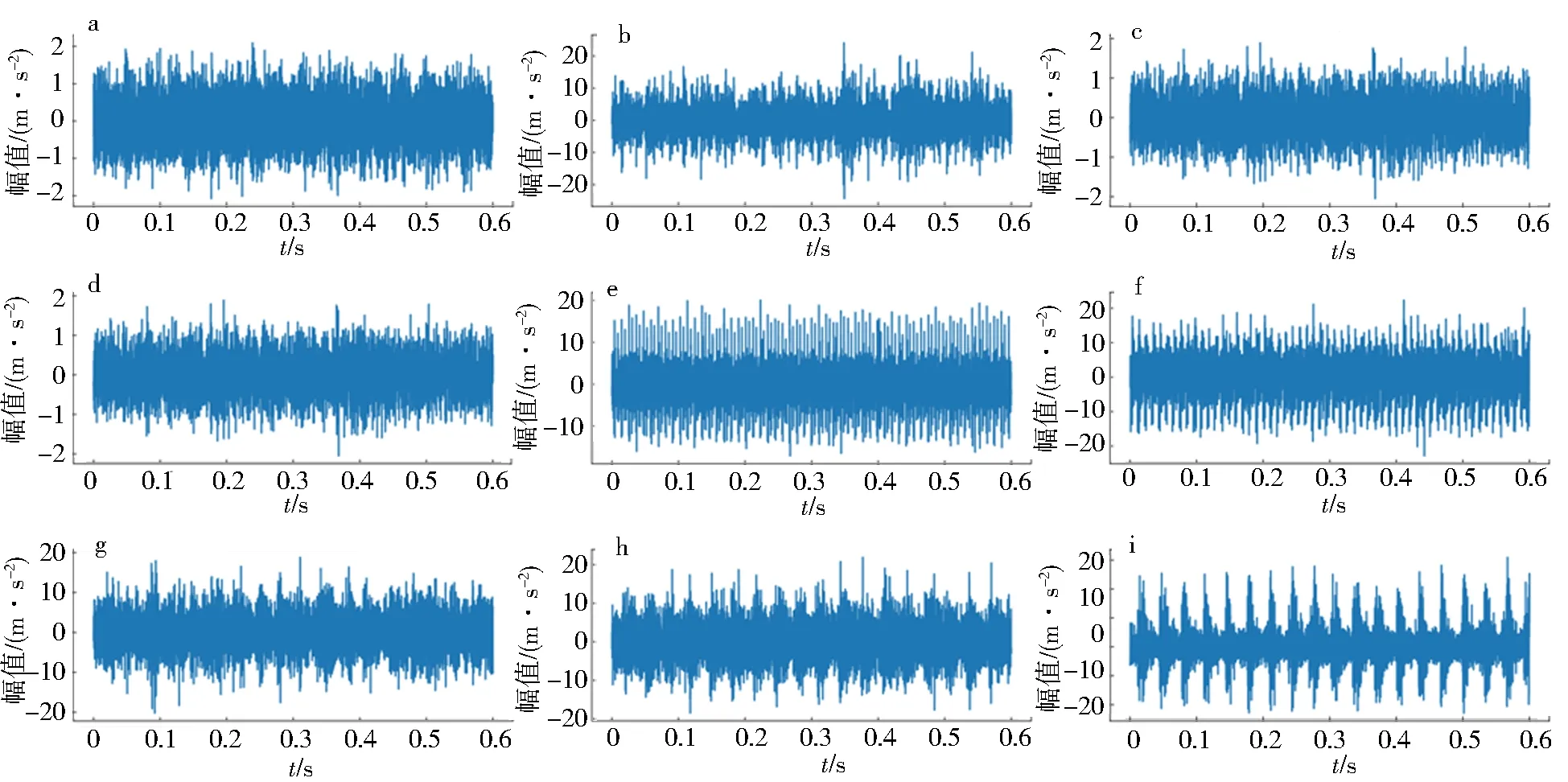
a.正常;b.工况1外圈故障;c.工况1保持架故障;d.工况2内圈故障;e.工况2外圈故障;f.工况2保持架故障;g.工况3外圈故障;h.工况3内圈故障1;i.工况3内圈故障2图11 西安交通大学轴承实验台9类信号时域图Fig.11 Time domain diagram of 9 types of signals of bearing test bench of Xi'an Jiaotong University

保持HHO-CNN和CNN模型的参数不变,利用CNN模型对西安交通大学轴承实验台的数据进行分类得到的结果如图12所示,CNN模型在迭代20次以后收敛,准确率为95%,损失率迭代100次以后仍未收敛.

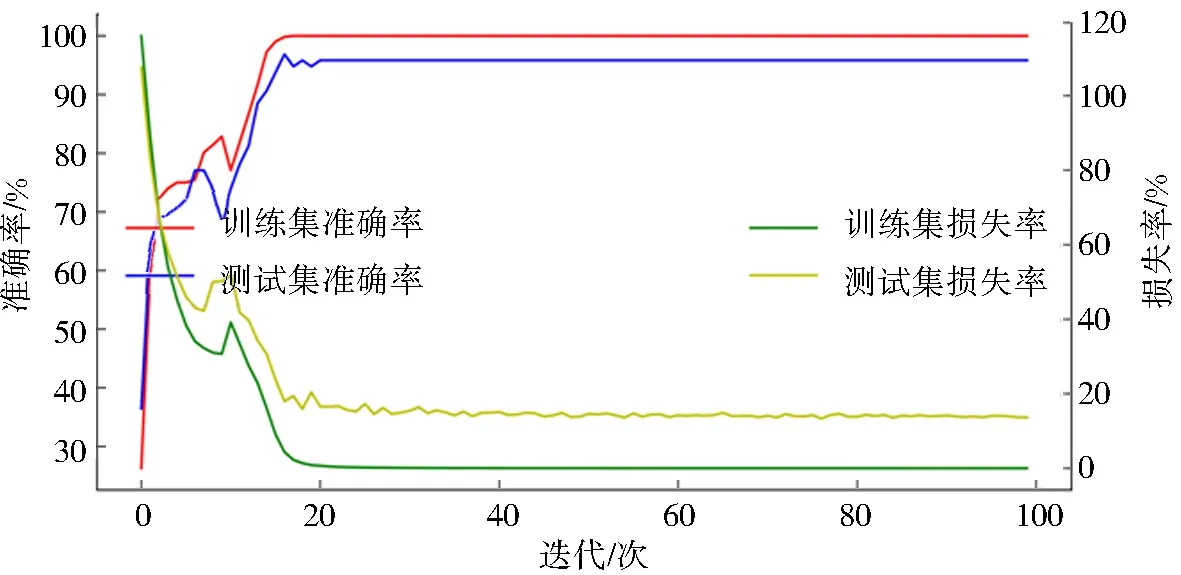
图12 9类信号CNN模型实验结果Fig.12 Experimental results of the CNN model for 9 types of signals

利用HHO对CNN进行优化,HHO优化后的迭代次数为70,全连接层的单元数为68,得到的结果如图13所示.准确率迭代10次以后收敛,保持在98%,损失率迭代10次以后保持在7%.

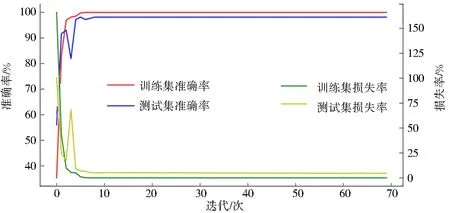
图13 9类信号HHO-CNN模型实验结果Fig.13 Experimental results of the HHO-CNN model for 9 types of signals

图14所示为9种不同类型轴承故障的混淆矩阵,HHO-CNN模型在标签2、4、7出现了分类错误,CNN模型仅在标签0、3、5分类正确,其他标签都存在错误.

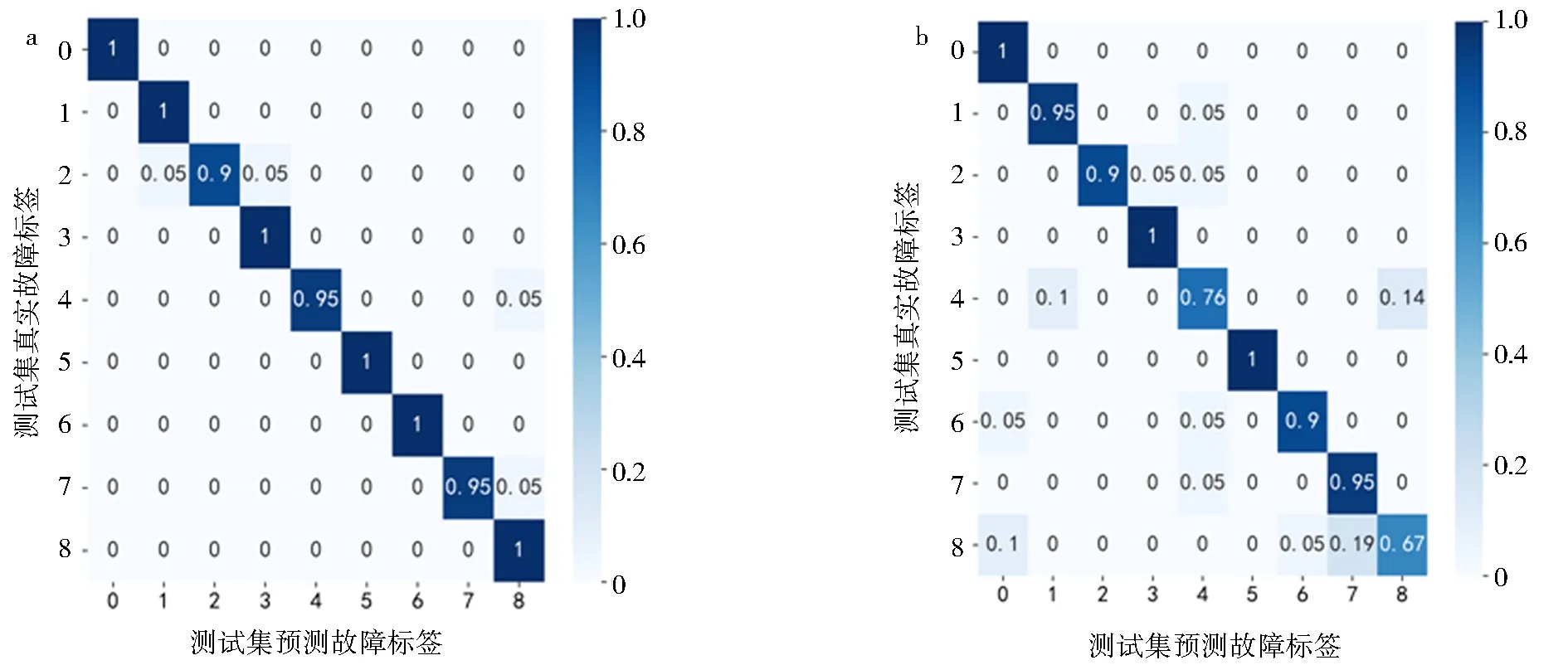
a．HHO-CNN混淆矩阵;b．CNN混淆矩阵图14 HHO-CNN和CNN模型实验结果对比Fig.14 Comparison of the experimental results of the HHO-CNN and CNN models

为直观展示模型的优化过程,采用T-SNE可视化将高维特征映射到二维空间,如图15所示.在图像输入层中,同一类别的数据点相对杂乱、分散,很难对每种故障类型进行分类.通过构建CNN模型和设置CNN模型参数,能够将同一类型的数据点进行归纳,但是错分的数据比较多,通过HHO算法优化,搜寻最优参数,得到最终的分类结果,仅有2、4、7识别错误,存在少数数据点错分,其他样本之间彼此远离.

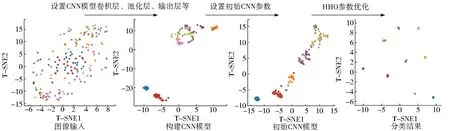
图15 T-SNE可视化Fig.15 T-SNE visualization

3.3 模型对比

为了评估HHO-CNN轴承故障检测模型的优势,同时选择GA-CNN、PSO-CNN、WOA-CNN[14-15]作为参照模型进行比较.在保持CNN模型其他参数不变的前提下,利用这4种优化算法共同优化全连接层的单元数量,结果如图16所示.图16表明HHO-CNN模型在准确率、损失率和计算速度方面优于其他3种模型.

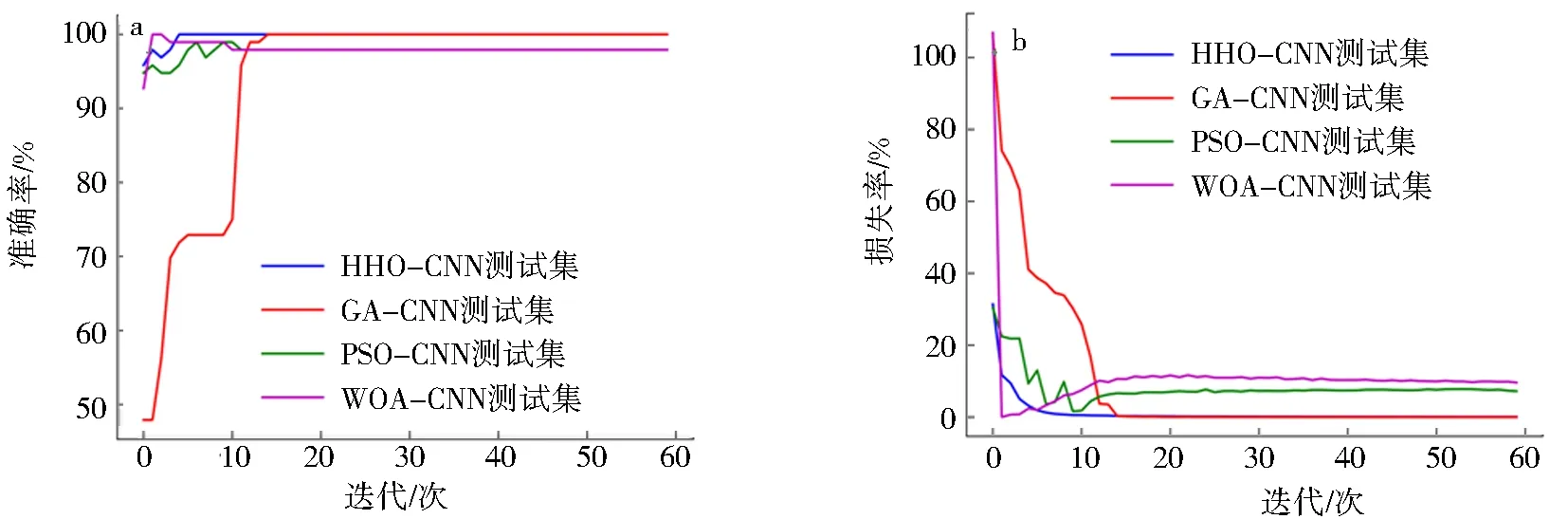
a.准确率;b.损失率图16 4类优化模型分类结果对比Fig.16 Comparison of the classification results of four optimized models

以RMSE(均方根误差)、MAE(平均绝对误差)衡量模型预测误差,数值越小说明模型的预测效果越好.R2(决定系数)用来衡量模型预测能力,数值越接近1说明模型的预测效果越好.4种模型分析对比结果如图17所示.图17表明HHO-CNN模型优于另外3种模型.

4 结论

针对CNN模型进行模式识别过程中的超参数问题,尤其是在处理多分类时由超参数引起的准确率低、收敛速度慢等情况,提出了一种HHO-CNN方法.

1)HHO对CNN模型的超参数空间进行优化,具有高效的探索和利用表现,使得CNN结构更适合轴承故障数据集的复杂性,增强了模型学习数据中复杂模式的能力.

2)得益于HHO以适应度最优为目标的参数捕获和位置更新能力,使得全连接层的单元数量和迭代次数可以实现迅速收敛,并将优化后全连接层的单元数量和迭代次数赋值给CNN模型,表现出更高的诊断准确性、更高的精度、更快的运算速度以及更少的内存占用率.

3)通过轴承多故障分类数据验证了所提方法对不同故障类型和故障程度数据集的模式识别效果.