轮轨激励条件下轴箱轴承内圈故障振动特性分析

邓飞跃,王红力,高瑞洋,李浩

(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.河北省工程机械动力与传动控制重点实验室,河北 石家庄 050043)

高速列车轴箱轴承一般采用双列圆锥滚子轴承,具有较为复杂的机械结构,时刻承受着来自车辆与轨道之间复杂激励的作用,因此有必要建立更为准确的轴箱轴承故障动力学模型,深入开展故障轴承动力学行为研究,为更好地进行轴承故障诊断奠定理论基础.

近年来,有关故障轴箱轴承动力学行为的研究得到了广泛关注.曾京等[1]采用Simpack软件建立考虑轴箱轴承表面波纹度缺陷的动力学模型,分析其对车辆振动特性的影响.丁东升等[2]使用Solidwork和ADAMS建立含外圈故障的列车轴承动力学模型,分析了不同故障位置下振动响应特性;刘永强等[3]建立了轴箱轴承非线性动力学模型,进行了正常与外圈故障下轴承动力学行为规律研究;Ma等[4]通过分析轴箱轴承内、外圈故障模型,研究了不同故障程度及不同转速下轴承的振动特性.刘建新等[5]构建了列车轴承外圈滚道剥离故障模型,对轴承故障状态下振动响应进行了分析.但是,上述研究大多构建的都是含故障的单一轴承动力学模型,没有考虑轴箱轴承内圈与列车轮对配合时受到轮轨之间复杂激励的作用.

将轴箱轴承集成于车辆-轨道动力学模型中,更符合列车轴承动力学分析的实际工况.曹青松等[6]建立了车体-构架-悬挂-滚动轴承-轮轨的垂向耦合动力学模型,研究了不同间隙量和行驶速度下,列车轴承支承松动的非线性动力学特性.Wang等[7]通过分析轴箱轴承与车辆-轨道耦合动力学模型,研究了轨道不平顺激励下轴承的振动响应.Li等[8]基于轴承非线性时变接触载荷,建立了车辆-轨道模型,分析了轨道不平顺激励下车辆的振动特性.易彩等[9]建立了一种包含柔性轮对的轴箱轴承-车辆-轨道耦合动力学模型.任尊松等[10]则构建了考虑轴箱轴承与列车各部件耦合关系的车辆-轨道动力学模型.上述研究为更加准确地分析轴承动力学行为提供了积极的借鉴意义,但是上述研究针对的大都是健康轴箱轴承动力学模型,缺少对含故障的轴箱轴承动力学行为研究.

基于上述分析,本文采用多体动力学分析方法,将轴箱轴承动力学模型与车辆-轨道动力学模型相融合,考虑轮轨之间复杂激励的影响,对含内圈剥离故障的轴箱轴承动力学行为进行了深入研究,通过滚振实验台轴箱轴承实验进行了验证分析.研究结果为高速列车轴箱轴承故障机理分析与运营维护提供了一定的理论基础.

1 车辆-轨道系统动力学模型分析

在UM中构建的高速动车组单节车辆动力学模型由车体、构架、轮对与转臂轴箱等组成,车辆系统拓扑关系如图1所示.UM中将轴箱、构架和车体设置为邻接刚体约束,各主要部件组成及其自由度如表1所示.一系阻尼力具有非线性粘弹力特性,二系垂向减振器具有线性力特性,二系横向减振器具有散点特性,抗蛇行减振器具有线性粘弹力特性.

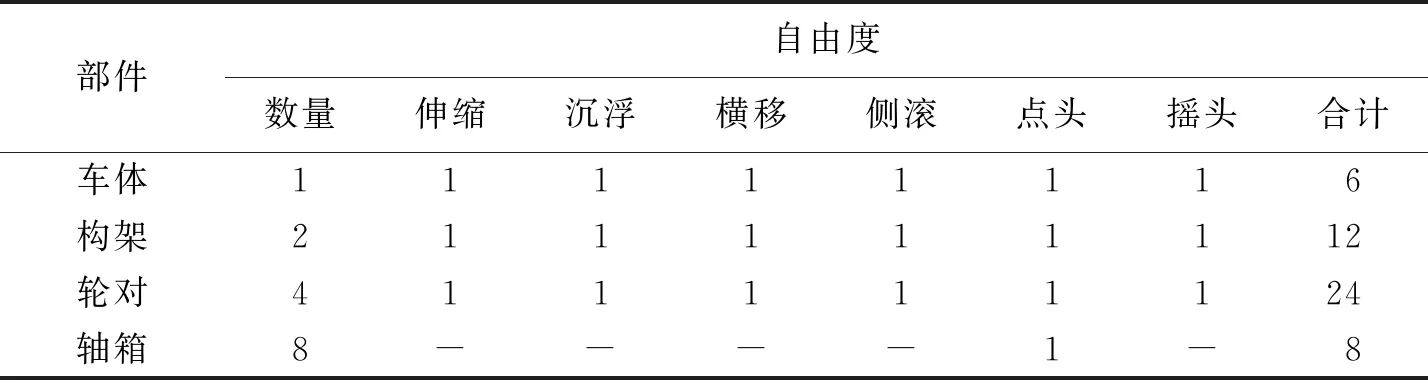
表1 车辆系统组成及自由度

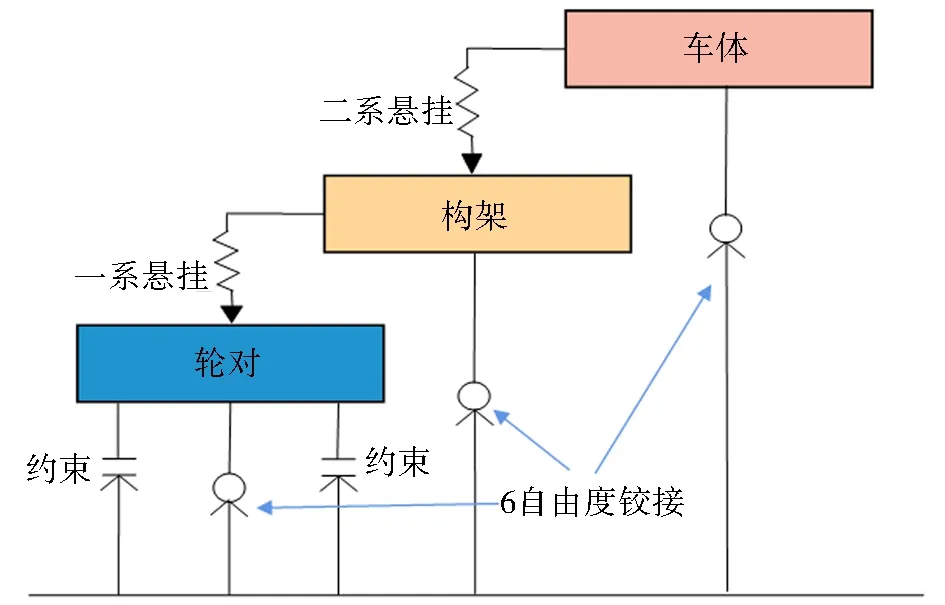
图1 车辆动力学模型拓扑图Fig.1 Topology map of vehicle dynamic model

钢轨型号选取CN60轨,车辆踏面为S1002CN型踏面,轮轨接触通过UM软件进行非线性化处理.根据CRH380B高速动车组及转向架相关参数,构建转向架模型与单节车辆-轨道系统模型如图2所示.

a.转向架;b.车辆-轨道系统图2 系统动力学模型Fig.2 System dynamic modeling

从车辆运动稳定性、平稳性和安全性3个方面对所构建车辆-轨道系统动力学模型进行验证.采用减速法计算车辆模型临界速度如图3所示.从图3中可知车辆达到稳定状态时,临界速度为709.2 km/h,满足车辆运动稳定性要求.Sperling指标W是评价车辆运行平稳性常用指标,车辆模型在直线轨道上仿真运行,轨道不平顺选取实测线路“京津谱”轨道激励,车速分别设置为290、300、310 km/h,计算车体前后2个点的Sperling指标见表2.从表2中可知,测点1和测点2的横向Sperling指标均在1.6以下,垂向Sperling指标均在1.3以下,满足国家规定2.5以内的标准.计算车辆模型运行安全性指标脱轨系数与轮轴横向力,结果见表2.车速在290～310 km/h,车辆的最大脱轨系数在0.16以下,轮轴横向力最大为10 592 N远小于规定极限值,脱轨系数和最大轮轴横向力也都满足国家标准规定.通过对车辆运动稳定性、平稳性和安全性的验证,证明了所建立的车辆-轨道系统动力学模型的准确性.

表2 车辆系统的指标评价

图3 临界转速分析Fig.3 Critical speed analysis

2 轴箱轴承动力学建模

2.1 轴箱轴承载荷分析

轴箱轴承内圈与轮对连接,外圈匹配在轴箱箱体内,分别与一系弹簧、一系垂向减振器以及转臂相连,再与转向架构架相连,如图4所示.列车实际运行中,转向架中一系弹簧、一系垂向减振器和轴箱转臂等多个部件,在列车自重、轮轨激励、转臂运动等作用下对轴箱轴承有着非常复杂的载荷冲击.

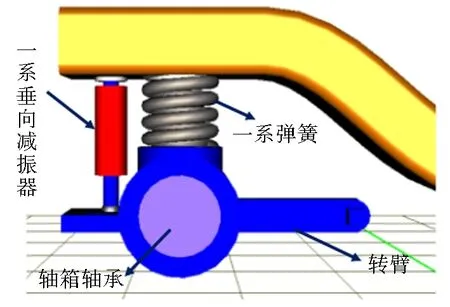
图4 轴箱轴承安装位置Fig.4 Installation position of axlebox bearing

为了更好地考虑轨道激励对轴箱轴承振动冲击的影响,在高速动车组整车动力学仿真中,将真实的“京津谱”作为轨道激励,分别计算一系弹簧、一系垂向减振器和轴箱转臂,对轴箱横向、纵向和垂向3个方向上的载荷数值,并分别按3个方向进行叠加,得到的轴箱轴承载荷谱见图5.轴箱轴承在横向、纵向和垂向3个方向上所受载荷均在轮轨激励作用下沿时间轴有着明显的变化,其中垂向载荷最大,是轴箱轴承所承受主要载荷.

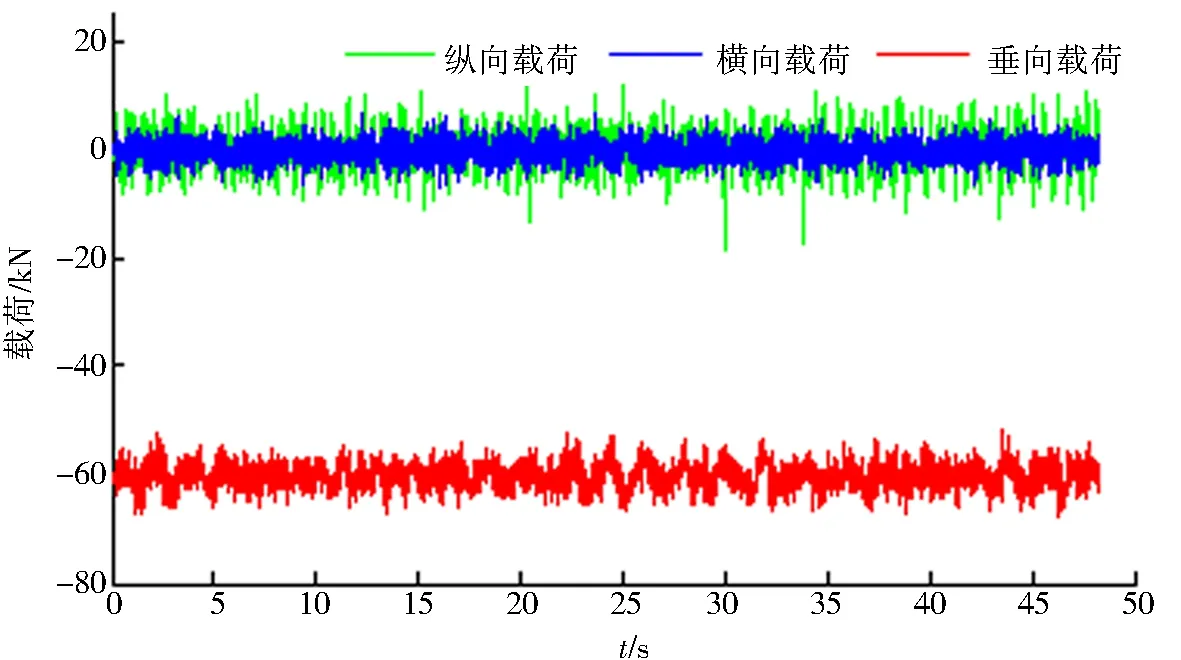
图5 轴箱轴承所受载荷Fig.5 Load of the axlebox bearing

2.2 轴箱轴承三维模型的建立

以CRH380B高速动车组采用的德国FAG系列双列圆锥滚子轴承为对象,选取其相关参数,使用Solidwork软件分别构建轴箱轴承外圈、内圈、滚子、保持架、隔圈等零件三维模型结果如图6所示.

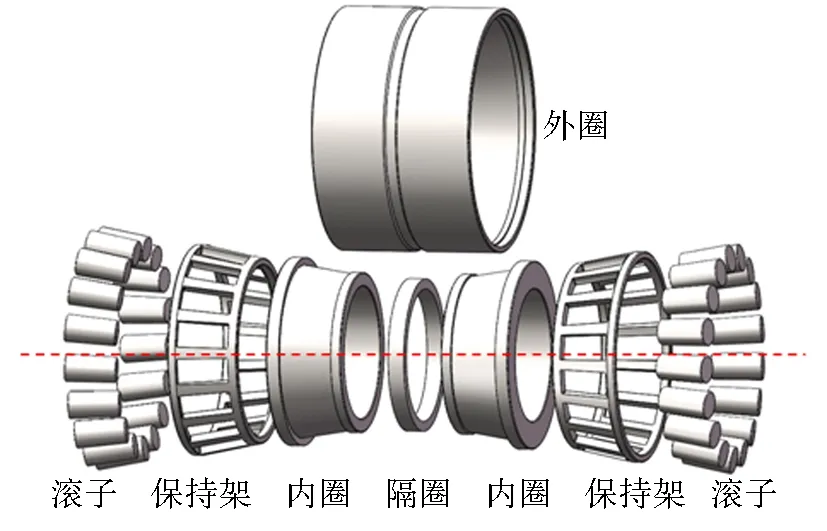
图6 轴箱轴承零件三维模型Fig.6 3D model of axlebox bearing parts

列车运行中,轴箱轴承内圈故障频率会被转轴旋转频率不断调制.故障位于加载区域时,故障冲击剧烈,振幅较高;移出加载区域后,振幅又会显著降低.因此,相比外圈故障,轴箱轴承发生内圈故障时,轴承系统振动响应更为复杂.基于此,在轴承内圈滚道仿真了剥离故障,故障尺寸为48 mm×2 mm×1 mm,内圈故障模型见图7a,各轴承零件装配完毕后见图7b.

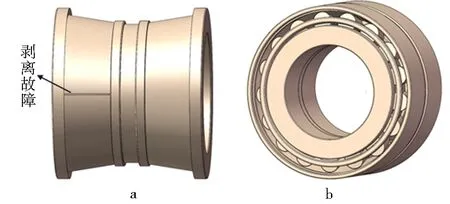
a.内圈故障;b.轴承装配体图7 轴箱轴承故障模型Fig.7 Fault model of axlebox bearing

2.3 轴箱轴承三维模型建立

将已建立的轴箱轴承装配体模型以Parasolid格式导入至ADAMS/View中.依据轴承运动关系,轴承内圈与地面间添加旋转副驱动进行驱动;外圈与地面间添加扭簧固定.轴箱轴承模型包含34个滚子、2个保持架、1个外圈、2个内圈、1个隔圈,其中滚子、保持架、外圈均有6个自由度,内圈与隔圈均设置1个旋转副,共计225个自由度.此外,滚子与内、外圈、保持架之间,隔圈与内圈之间通过宏命令方法来定义接触关系,共计104个刚性接触.鉴于列车运行过程中,轴箱轴承承载区域在轴承上方[11],将车辆-轨道系统中得到的轴箱轴承垂向载荷均分为3组施加于轴承外圈上方,指向轴心.横向载荷和纵向载荷则分别添加于轴承内圈质心处,轴承动力学仿真时间设置为1 s,仿真步长为0.001 s.

3 实验验证与分析

3.1 实验介绍

高速动车组轴箱轴承实验是在交通工程结构力学行为与系统安全国家重点实验室高速列车单轮对滚振实验台上进行的.该实验台结构如图8a所示.实验台下方有2个驱动轨道轮,每个轨道轮分别由2台液压激振器提供横向和垂向激振,因此实验台可以同时进行滚动和振动加载,能够模拟高速列车时速500 km/h以内不同速度等级、不同激扰条件下轴箱轴承跑合振动测试实验.实验台上拾振器安装在测试轴承端盖上方,如图8b所示.选取轴箱轴承实际运行出现的内圈剥离故障(图8c所示)进行测试,故障尺寸大小与故障仿真模型基本相同,验证了所建立的内圈剥离故障模型的准确性.实验过程中轴承转速设置为1 800 r/min,采样频率为25 600 Hz.通过计算,得到轴承内圈旋转频率和故障特征频率分别为fr=30 Hz、fi=290.9 Hz.

a.高速列车轴箱轴承综合实验台;b.传感器测点;c.内圈剥离故障轴承图8 轴箱轴承实验Fig.8 Axlebox bearing test

3.2 验证分析

实验得到的轴箱轴承内圈故障信号时域波形如图9a所示,信号波形中周期性的故障冲击成分比较明显.仿真信号波形如图9b所示,由于轮轨激励的影响,虽然存在一定程度的干扰,但仍可观察到故障冲击成分.包络解调分析结果如图10所示,实验信号包络谱中可以发现清晰的转频成分、内圈故障频率fi以及周围的边频带(图10中红色虚线部分),这符合轴承内圈故障特征频率受转频调制的特点.仿真信号包络谱中也可以提取出转频、故障频率以及相应的边频带,这与实验信号结果相同,证实本文所建立的轴承内圈剥离故障模型较为准确.

a.测试;b.仿真图9 轴箱轴承内圈故障信号的时域波形Fig.9 Time domain signal of axlebox bearing with inner race fault

a.测试;b.仿真图10 轴箱轴承内圈故障信号的包络谱Fig.10 Envelope spectrum of axlebox bearing with inner race fault signal

选取文献[2]方法,仅在轴承上施加定载荷作用,而不考虑轮轨激励的影响,对内圈故障轴承振动特性开展分析,结果如图11所示,图11中蓝色部分为定载荷下仿真的结果.从图11可知定载荷下周期性故障冲击成分非常明显,几乎没有噪声干扰成分,对应包络谱中也仅出现非常明显的转频、内圈故障频率及边频带.而本文仿真的内圈故障信号波形中包含有一定程度的噪声干扰,频谱中也出现明显的杂频成分,这是由轮轨激励导致的.由此得出结论,高速列车实际运行中,轮对激励对轴箱轴承动力学行为有着不可忽视的影响.

a．时域波形; b.包络频谱图11 故障振动特性对比分析Fig.11 Analysis comparison of vibration characteristics of fault

4 动力学仿真分析

4.1 转速分析

轴承内圈转速分别设置为1 500、1 800 r/min,得到保持架、滚子转速仿真结果如图12、13所示,转速仿真结果与理论值对比结果如表3所示.从表3可知,保持架转速理论值与仿真值较为接近,误差为1.03%.轴箱轴承模型的几何误差、润滑状态误差、滚子存在歪斜、倒角、倒棱等因素导致滚子转速仿真值误差稍大,理论值与仿真值误差为6.57%,仍在合理范围内.

表3 保持架、滚子转速仿真结果

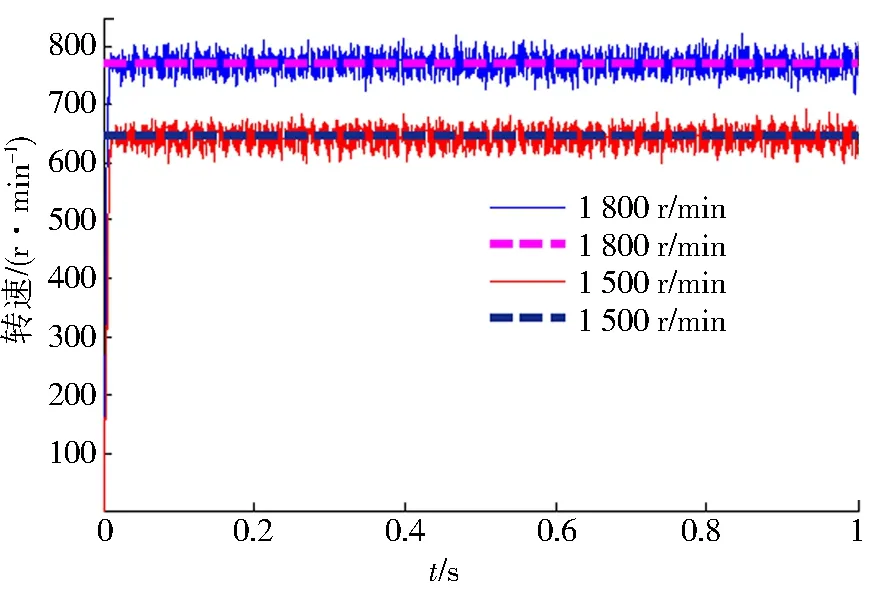
图12 保持架转速仿真结果Fig.12 Simulation results of rotational speed of cage

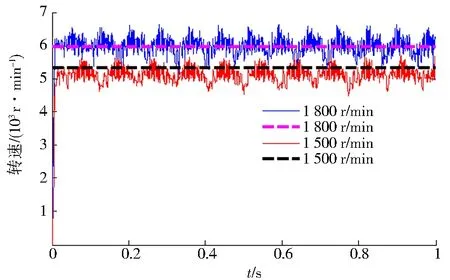
图13 滚子转速仿真结果Fig.13 Simulation results of rotational speed of roller

4.2 接触载荷分析

在轴箱轴承模型中随机选取某一滚子,分析其与内、外圈滚道接触载荷的变化.图14a是故障侧滚子、非故障侧滚子与轴承内圈滚道接触载荷的变化;图14b是轴承非故障侧滚子、正常轴承滚子接触载荷的变化.滚子运动至轴承上方承载区域时,载荷明显增大,运动至非承载区域时,载荷显著减小,接触载荷呈现周期性的波峰分布.故障侧滚子与内圈滚道的接触载荷要大于非故障侧,正常轴承滚子与内圈接触载荷则要小于非故障侧轴承滚子,接触载荷大小整体呈现出“故障侧大于非故障侧,非故障侧大于正常轴承”的特点,这说明内圈故障的存在导致轴承冲击载荷显著增大.图15给出了滚子与外圈接触载荷的变化,滚子运行至承载区,与外圈接触载荷达到最大,载荷方向与滚子内圈接触载荷方向相反,故障侧接触载荷最大,非故障侧次之,正常轴承的最小.图16显示了考虑轮轨激励下与定载荷条件下轴承故障侧滚子与内、外圈接触载荷的变化,考虑轮轨激励条件下滚子与内、外圈的接触载荷要明显大于定载荷条件下.

a．内圈故障轴承;b.故障轴承与正常轴承图14 滚子与内圈接触载荷的变化Fig.14 Contact load change between roller and inner race

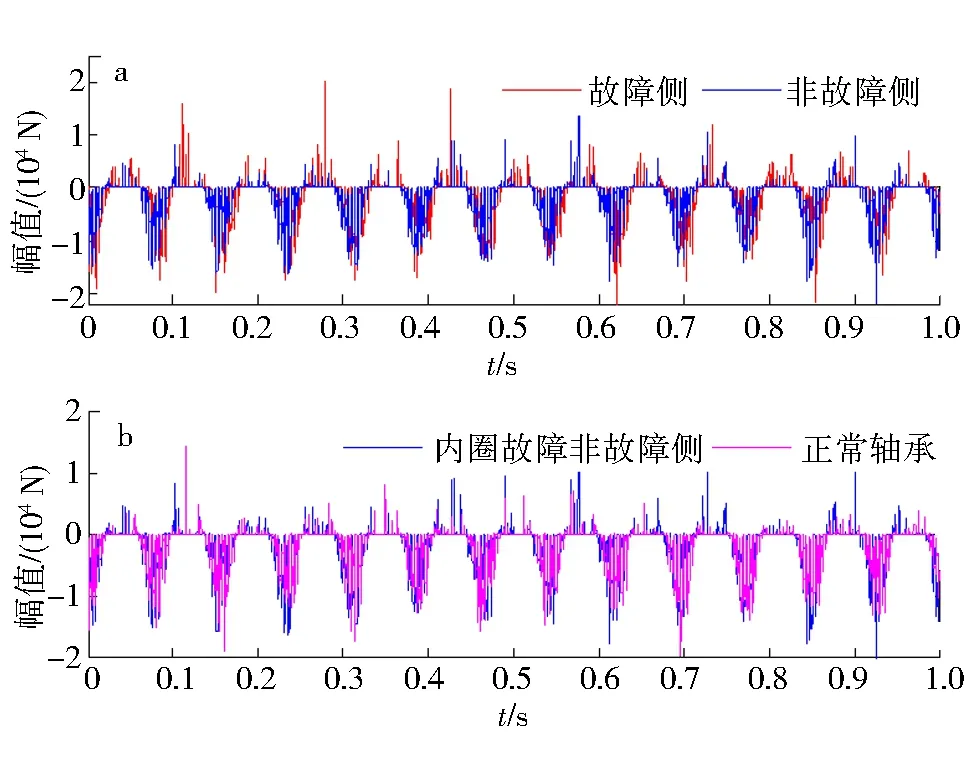
a．内圈故障轴承;b.故障轴承与正常轴承图15 滚子与外圈接触载荷的变化Fig.15 Contact load change between roller and outer race

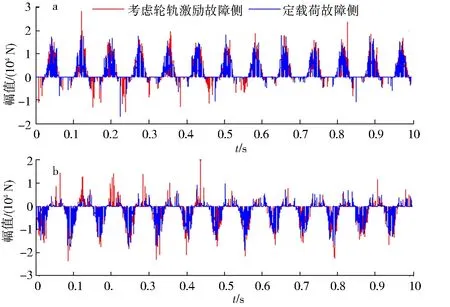
a.滚子与内圈之间;b.滚子与外圈之间图16 不同条件下接触载荷的变化Fig.16 Contact load change under different conditions

4.3 质心运动轨迹分析

传统分析质心轨迹的方法是观察轨迹的变化范围,本文在此基础上引入盒维数(box dimension,BD)指标作为量化评判质心混乱程度的依据.根据盒维数计算原理[12],分析轨迹二维图像,定量得出质心轨迹的复杂程度.

考虑轮轨激励条件下,轴箱轴承保持架在X-Z平面的质心运动轨迹如图17所示.故障侧保持架质心轨迹波动范围X方向为-0.5～0.6 mm,Z方向为0.1～0.9 mm,相比非故障侧质心运动范围更广,轨迹也更杂乱无章,故障侧的BD要明显大于非故障侧质心轨迹BD.这说明当轴承一侧发生内圈故障时,故障侧保持架的振动更为强烈.正常轴承的保持架质心波动范围最小,杂乱现象很轻微,BD为1.590 6,数值最小.内圈故障的出现导致轴承保持架稳定性变差,出现了明显的保持架质心轨迹波动.考虑轮轨激励与定载荷下,故障轴箱轴承保持架质心轨迹变化如图18所示,轮轨激励使得保持架质心轨迹更为混乱.

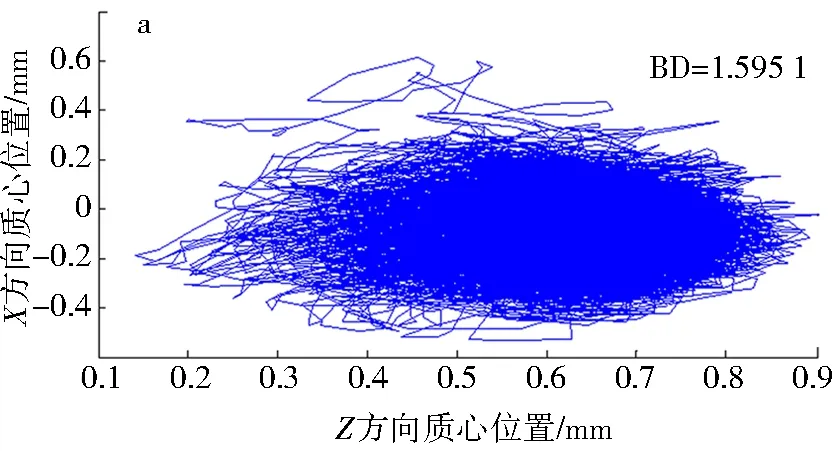
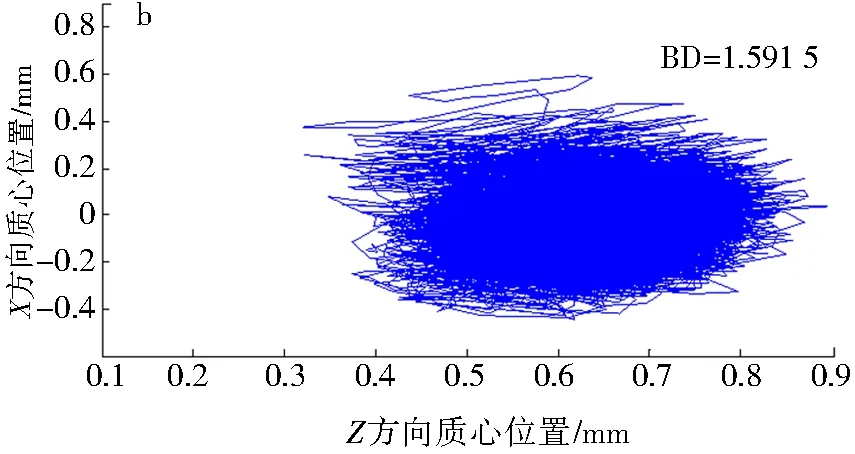
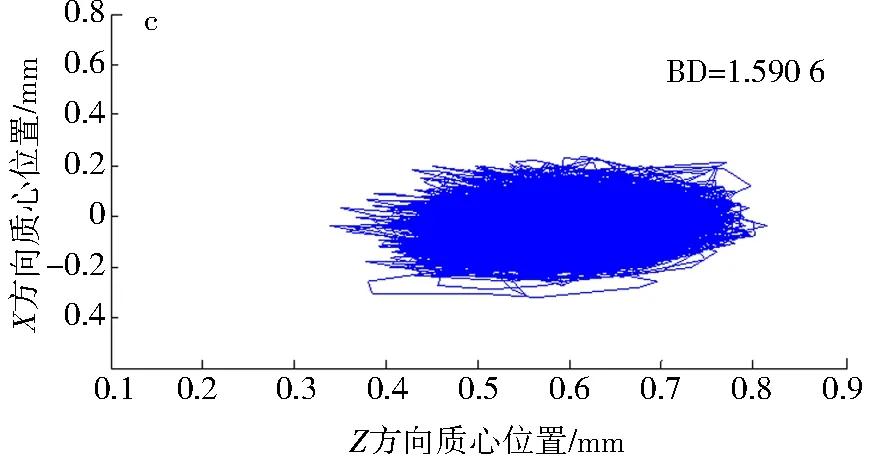
a.故障侧;b.非故障侧;c.正常轴承图17 考虑轮轨激励条件下保持架质心轨迹 Fig.17 Trajectory of the mass center for bearing cage under wheel-rail excitation

图18 不同条件下保持架质心运动轨迹Fig.18 Trajectory of the mass center for bearing cage under different conditions

考虑轮轨激励条件下,故障轴承与正常轴承的外圈质心运动轨迹如图19所示.故障轴承外圈质心波动范围更大,轨迹更为杂乱,BD为1.679 5,明显大于正常轴承BD值1.675 4.这说明轴箱轴承内圈故障也会引起外圈异常振动,破坏了外圈运动的稳定性.考虑轮轨激励与定载荷条件下,故障轴承的外圈质心轨迹如图20所示,轮轨激励影响下外圈振动非常混乱,不可避免地会引发噪声,一定程度上会淹没内圈故障的振动特征,使得故障特征难以识别.综上可知,轮轨激励使得轴箱轴承内部各个元件间的接触载荷、保持架与外圈的振动更为复杂,对故障轴承的动力学行为带来了不可忽视的影响,只有考虑轮轨激励的影响,才能准确揭示故障轴箱轴承振动特性规律.

a.故障轴承;b.正常轴承图19 考虑轮轨激励条件下轴承外圈质心轨迹Fig.19 Trajectory of the mass center for outer ring under wheel-rail excitation

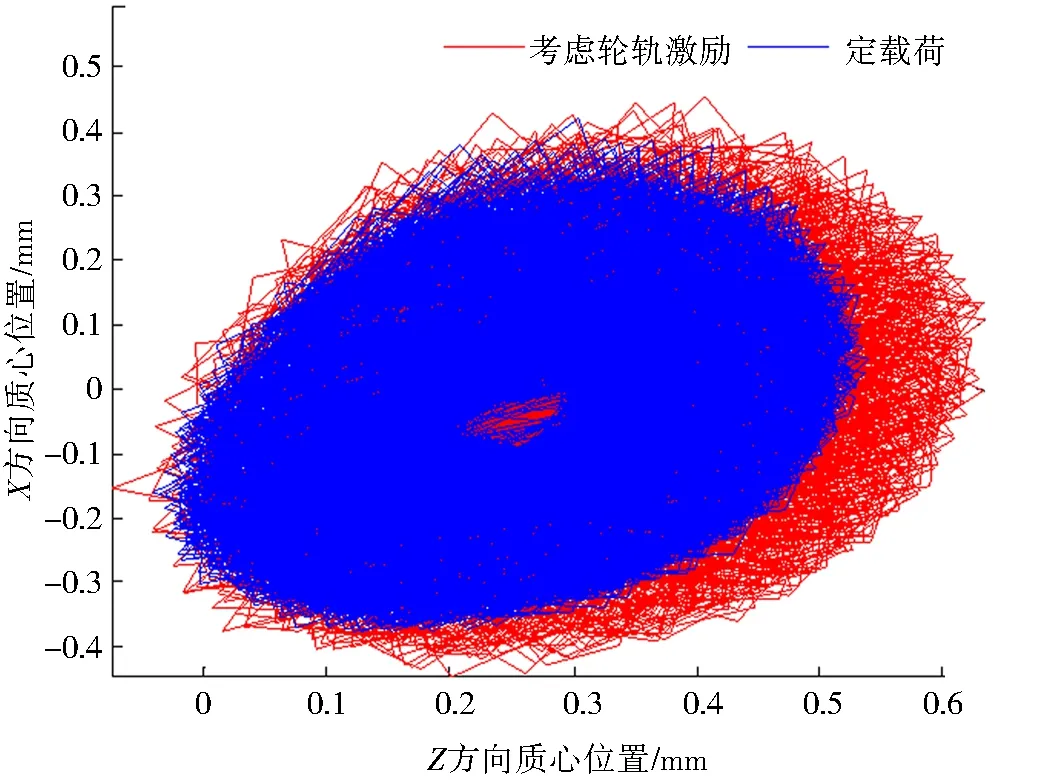
图20 不同条件下外圈质心运动轨迹Fig.20 Trajectory of the mass center for outer ring under different conditions

5 结论

建立了车辆-轨道动力学模型,基于稳定性、平稳性和安全性分析验证了模型的准确性,并通过获取轴箱轴承所受的垂向、纵向和横向载荷,考虑了轮轨复杂激励的影响.对轴箱轴承内圈故障振动分析可知,轴箱轴承滚子与内、外圈接触载荷呈现周期性的分布,故障侧接触载荷要明显大于非故障侧,内圈故障冲击破坏了保持架的稳定,保持架与外圈质心波动更为剧烈,导致轴承动力学行为更加复杂.