基于改进果蝇算法的多频组合中长期电力负荷频率自抗扰控制方法
肖 成
引言
多频组合电力系统具有出力不确定性的特性,对系统频率的稳定性造成了严重威胁。针对中长期电力负荷频率的波动问题,本文采用改进果蝇算法设计了一种电力负荷频率控制方法,赋予控制过程的自抗扰属性,实现电力负荷频率自抗扰控制。
一、电力负荷频率自抗扰控制方法设计
多频组合中长期电力负荷具有静态和动态的特性,通常情况下,当系统稳定运行时,负荷频率也呈稳态特性变化;当系统联结出现波动时,负荷频率体现出动态变化特性[1],因此,为在不同条件下更好地控制电力负荷频率,本文设计内模负荷频率控制器实现频率自抗扰控制。
内模控制具有结构简单、运算简便的优势,是其他一些需要通过模型来实现控制器设计的方法的依据。P表示被控制对象;Q表示控制器中的跟踪微分器;Qd表示自抗扰内模控制器。
本文设计的电力负荷控制器包含三个子控制器,分别为跟踪微分器(TD)、扩张状态观测器(ESO)以及非线性组合部件(NLSEF),通过三个子控制器的单独控制,计算扰动估计值和步长输出值,之后将输出结果进行拟合,得到最终控制器。
首先对对象模型δ进行分解,分为两个部分[2-3]:
扩张状态观测器(ESO)的控制过程为[4]:
非线性控制(NLSEF)可将微分器与观测器的输出量进行综合控制,其控制过程为[5]:
将式(1)~(4)进行整合,并结合负荷频率动态模型,得到最终自抗扰内模控制器如下所示[6]:
根据负荷频率变化特性,将电力系统负荷频率动态模型分解为两个子模型,设计包含三个控制部分的自抗扰内模控制器,实现负荷频率的控制。
负荷频率控制器参数优化的目的在于在一定的搜索范围内找到合适的的值,使得控制器的输出值为最佳。在优化过程中,以负荷频率控制性能为适应度,设置初始算法的参数,然后运行负荷频率动态模型,得到目标函数适应值,将其与果蝇算法中的适应值相比较,如果满足迭代结束标志或者迭代次数等于最大迭代次数则结束搜索;若不满足精度要求返回循环。本文采用的是实数编码,编码形式为实数编码,对P控制器参数搜索中的每个果蝇个体的坐标编码:。
利用改进果蝇算法优化负荷频率控制器整定参数的具体步骤如下:
设置蝇群大小、个体数量、最大步长和群体位置等算法参数;
赋予果蝇一部分自适应搜索步长算法寻优,另一部分按固定步长寻优;
预计第K个体和原地位置之间的距离,估算味道浓度值;
将上一步计算得出的指标作为新的适应度函数值,并与初始适应度值比较,若满足条件则完成迭代,进而得到最佳的控制器参数,否则,重新确定群体中最优位置即味道浓度最高的地方,之后果蝇其他群体朝该位置坐标移动,生成新的果蝇群体,重复以上步骤,直到满足迭代终止要求,输出最优控制器整定参数。
利用改进果蝇算法,根据如上优化步骤对负荷频率控制器整定参数进行优化,以求得期望的控制性能的负荷频率控制器,使得频率控制结果符合实际应用需求。
二、实验论证
为测试文中所提电力负荷频率自抗扰控制方法的实际性能,选取典型多频组合中长期电力系统为研究对象,该系统的空调集群数量为台,频差死区,单体最大和最小输出功率限制分别为。在MATLAB/Simulink平台上,将上述相关参数输入或代入图1,获得具体的风电数据和负荷频率响应代码,由M文件编写并与系统模型连接,实现仿真过程。选取不同方法作为所提方法的实验对比方法。记文献[1]基于大变异遗传算法的负荷频率自抗扰控制为方法1,文献[2]基于一致性算法的负荷频率控制为方法2。

图1 随机负荷扰动
为测试基于改进果蝇算法的电力负荷频率控制方法在随机负荷扰动下的控制性能,根据随机负荷的变动情况,对系统输入如图1所示的随机负荷扰动。
如图1所示,随机负荷扰动具有变化不规律且无周期性的特点,利用该工况能够测试负荷频率控制方法的综合控制性能。
同时采用方法1方法2与文中方法对上图工况下的负荷频率进行自抗扰控制,不同方法的控制效果及对比如图2所示。
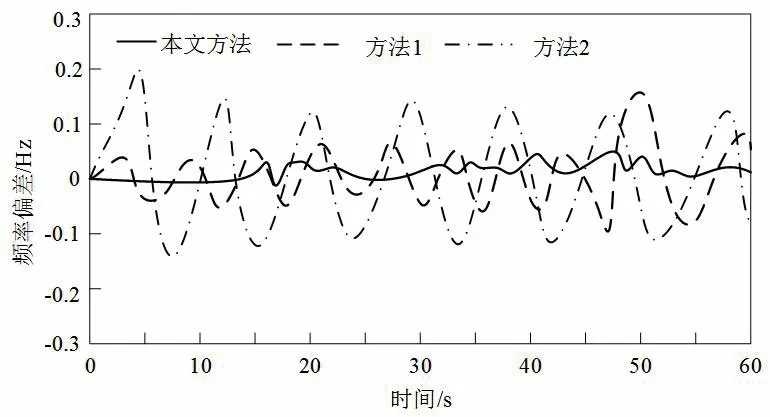
图2 随机负荷扰动下的负荷频率控制对比结果
从图2可以发现,文中所提方法对于随机负荷扰动的频率控制性能较为显著。
在电力系统中引入阶跃负荷,如图3所示。
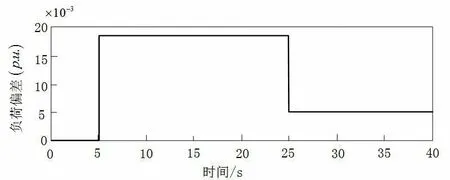
图3 阶跃负荷扰动
如图3所示,系统在第5s和第25s时分别受到0.018p.u.和0.018p.u.的上升与下降趋势的阶跃负荷扰动。
对受到阶跃负荷扰动下的系统进行频率控制,得到的控制效果及对比如图4所示。
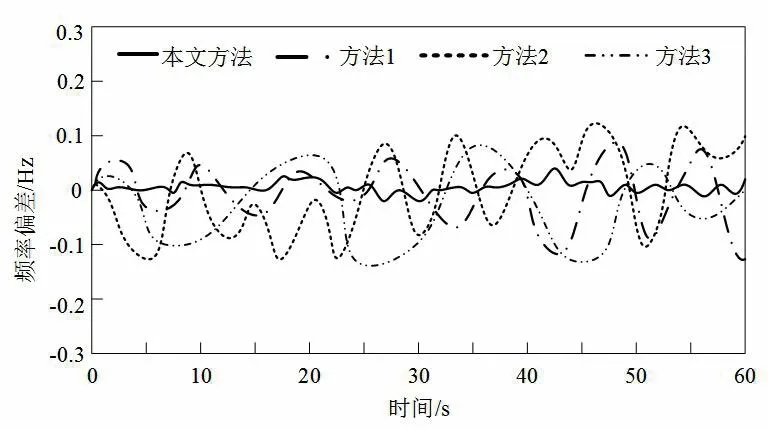
图4 阶跃扰动下的负荷频率控制对比结果
根据图4对比可知,自适应调节控制对象的最佳输出值,故对于阶跃负荷扰动下的负荷频率控制性能较好。
结束语
本文研究了多频组合中长期电力负荷频率自抗扰方法,并引入了改进果蝇算法优化频率控制器的整定参数,体现了基于改进果蝇算法的电力负荷频率自抗扰控制方法的有效性与优越性。

