基于改进随机森林的海量结构化数据异常辨识算法

宋冀峰

(中国政法大学, 刑事司法学院, 北京 100088)

0 引言

随着社会信息化水平的不断提升,网络中的结构化数据呈现爆发式增长。而面对如此海量的结构化数据,确定其中的异常数据能够充分满足高速存储应用、数据备份、数据共享以及数据容灾需求。但是由于结构化数据具有较高的复杂性,导致异常点识别精准率低与辨识耗时长的问题出现[1],因此寻找一种面向海量结构数据异常点辨识的方法是很有必要的。

为此相关研究人员陆续提出各种结构化数据辨识算法。文旭等[2]针对数据辨识精度差问题,提出一种基于因子分析的数据异常辨识算法。通过分解大数据负荷曲线,获得波动特征较为显著的随机分量,求解了随机分量中的异常数,但在实际应用中,这一算法仅适合于单个异常点检测,对于连续范围的异常点检测的效果差;殷浩然等[3]提出一种基于三维卷积神经网络的数据异常辨识算法,提取数据矩阵中的异常特征,利用三维卷积神经网完成辨识任务。但该算法的运行过程较为复杂,导致耗时增加。

为此,综合上述问题,提出基于改进随机森林的海量结构化数据异常辨识算法。随机森林作为一种深度学习算法,在数据异常点分类问题中的应用较为广泛,使用随机选择特征子集增加结构化数据中决策树的随机性,从而缩小异常检测的范围;通过局部敏感哈希算法对结构数据异常点度量,引入相关的向量空间,最终完成对数据异常辨识。

1 海量结构化数据去噪处理

由于原始结构化数据中存在大量环境噪声分量,这些均是大量不可用的数据,即噪声点,需要对数据中的噪声点进行去除。通过互补集合经验模态分解[4]方法,得到结构数据的本征模态函数,对本征模态函数分量进行重构,获得增强后的数据,实现数据去噪处理。

互补集合经验模态分解方法[5]主要依赖于经验模态分解方法,假设初始结构化数据信号为Z(t),在信号引入正值的随机白噪声[6]ui(t)与负值的随机白噪声-ui(t),此时的结构化数据信号表达式如下:

Zi(t)=Z(t)+ξ0ui(t),i=1,2,…,n

(1)

(2)

式(2)中,k代表最大相关熵。将正数值的随机白噪声的轮数进行到2M轮次数时,结合文献[8]的研究成果对于经验模态分解互补集合进行推理,其具体的表达式如下:

(3)

将经验模态分解集合结果与残差数值进行组合重构,获得去噪的结构化数据:

(4)

2 基于改进随机森林的异常数据范围确定

随机森林[9]是当前最广泛的分类器之一,通过随机选择特征子集来分裂决策树的节点,提高决策树的随机性,以此实现随机森林改进,进而提高结构化数据异常范围的确定精准度。

(5)

式(5)中,T代表超参数,fk(x)代表无剪枝的决策树,抽样数据集的预测公式为

(6)

式(6)中,I代表指示函数。AdaBoost算法有着非常优秀的泛化能力,该方法通过不断更新样本的权重,使决策树将精力都使用在之前的分类样本上,进而提高泛化能力,AdaBoost算法对随机森林进行T轮加权的具体公式如下:

(7)

式(7)中,αi代表每轮权重系数。经过i-1轮迭代随机森林模型表达式如下:

Fi-1(x)=α1f1(x)U1(x)+…+Ui-1(x)αi-1fi-1(x)

(8)

结合上述分析,搭建泛化风险函数,具体表达式如下:

(9)

(10)

3 结构化数据异常辨识方法设计

通过局部敏感哈希算法,在数据异常范围内训练数据,将牵引数据集按照不同类别进行分类,设定异常缩小范围后的数据Q,建立相应的哈希表。其在高斯分布中分布均匀,形成高斯矩阵A,通过结构化数据在高维空间中分布稀疏的情况,获得结构化数据的中空间几何坐标位置,假设结构化数据的异常特征向量用(wq1,wq2,…,wqj)表示,j代表结构化数据异常簇个数,wqj代表第j个异常簇在结构数据库中的比重,向量空间模型中结构化数据异常簇之间的相似度[11]表达式:

(11)

式(11)中,wij代表结构化数据异常簇频率[12]。通过概率设定阈值,完成异常数据的判断。

4 实验检测与分析

为了验证提出的基于改进随机森林的海量结构化数据异常辨识算法有效性,选择因子分析异常辨识算法与三维卷积神经网络算法进行对比实验。

实验的基础使用Windows 10系统,在仿真软件中设定二叉树为100,数据样本量为400 GB。

为了更深程度地对结构化数据进行异常点辨识,对结构化数据中的特征值与梯度值的变化曲线进行实验分析。

分析图1中的结构化数据特征值变化曲线可知,当时间周期为7、9、10的情况下,结构化数据特征值高于告警值,这说明结构化数据可能存在异常问题,因此这些数据中可能存在异常数据,非常适合进行后续实验。分析图2中的结果可知,所有周期的结构化数据梯度值均位于下告警值上方,且周期为8的情况下结构化数据梯度值超过了上告警值,说明非结构数据集合中的异常特征显著,这种幅度突增的关系显示了结构化数据存在异常点,以此为基础进行实验测试所得的结果具备真实性和可靠性。

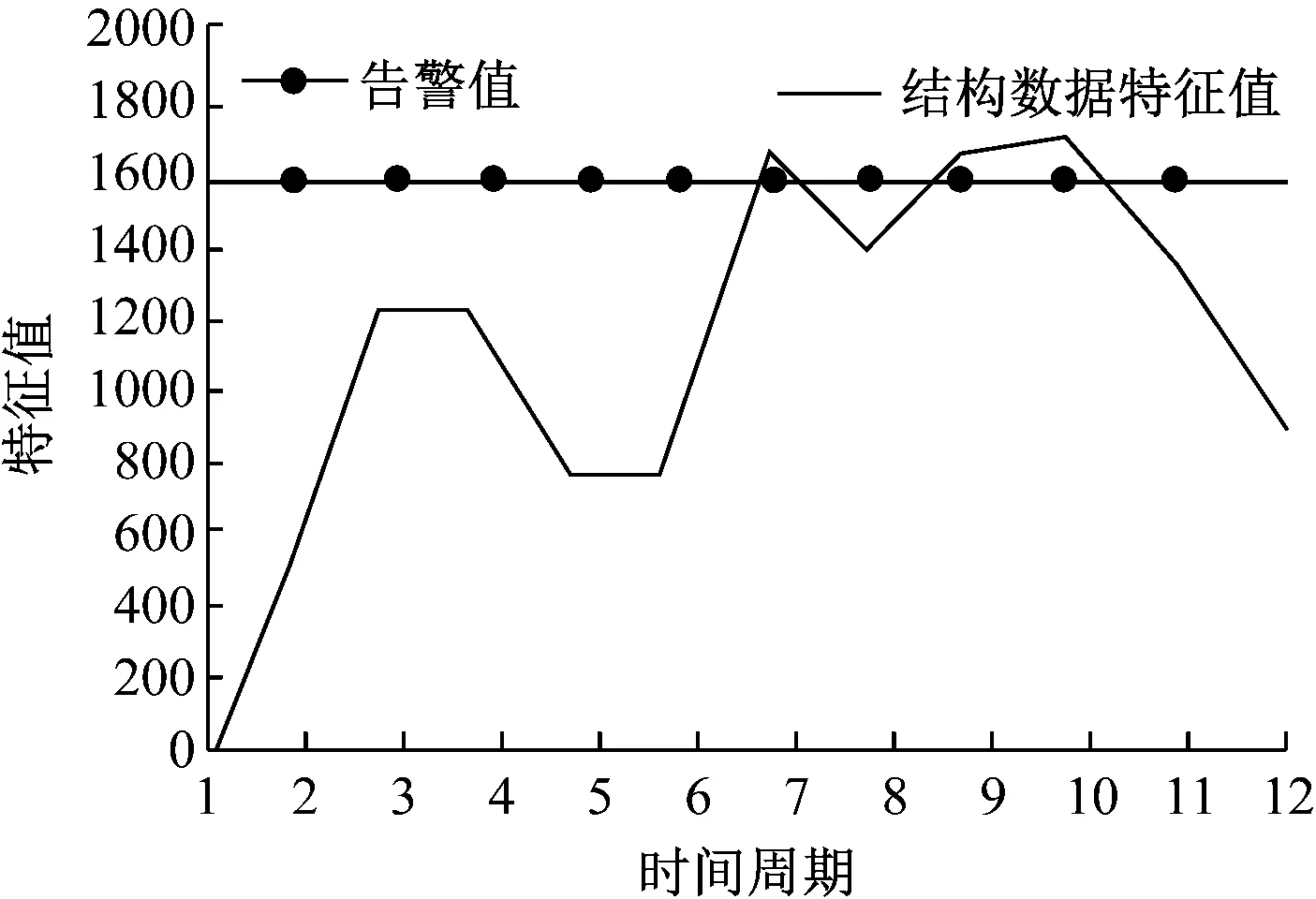
图1 结构化数据特征值变化曲线

图2 结构化数据梯度值变化曲线

海量结构化数据异常辨识精准度表示被正确标注为异常的数据在所有被标识为异常的数据中的比例,其中异常数据总量为5000个,则3种方法的异常数据辨识数量如表1所示。

表1 3种方法的异常数据辨识数量

结合上述数据得出3种算法的海量结构化数据异常辨识精准度对比结果,具体如图3所示。

图3 三种方法的辨识精准度对比结果

分析图3中的数据可知,随着实验次数的增加,3种算法的海量结构化数据异常辨识精准度均呈现显著的波动变化趋势。因子分析算法与三维卷积神经网络算法的辨识精准度都相对较低,且曲线浮动过于不稳定,精准度水平并不高。其中,因子分析算法的辨识精准度最大值为74.7%,最小值为61.9%;三维卷积神经网络算法的辨识精准度最大值为81.2%,最小值为68.4%。与实验对比算法相比,所提算法的异常数据辨识精准度最高,辨识精准度最高达到了95.8%,且精准度曲线相对稳定,这是由于所提算法使用随机选择特征子集增加了结构化数据中决策树的随机性,确定了异常范围,进一步提高了异常数据辨识精准度。

3种算法的异常数据辨识耗时数据如表2所示。

表2 异常数据辨识耗时数据

为了更为清晰的看到3种算法的辨识耗时的变化趋势,结合上述数据绘制辨识耗时对比结果图像,具体如图4所示。

图4 3种方法的辨识耗时对比结果

分析图4中的结果可知,随着结构化数据量的增加,3种算法的辨识耗时均呈现上升趋势。当结构化数据量为100 G的情况下,所提算法的辨识耗时为0.77 min,因子分析算法的辨识耗时为2.64 min,三维卷积神经网络算法的辨识耗时为1.85 min;当结构化数据量为200 G的情况下,所提算法的辨识耗时为1.79 min,因子分析算法的辨识耗时为5.74 min,三维卷积神经网络算法的辨识耗时为4.01 min;当结构化数据量为300 G的情况下,所提算法的辨识耗时为2.52 min,因子分析算法的辨识耗时为5.72 min,三维卷积神经网络算法的辨识耗时为4.51 min;当结构化数据量为400 G的情况下,所提算法的辨识耗时为2.52 min,因子分析算法的辨识耗时为5.72 min,三维卷积神经网络算法的辨识耗时为4.51 min。综合来看,所提算法的辨识耗时更短、效率更高。

5 总结

为了在海量数据中精准辨识数据结构化数据异常,其首要工作就是解决原始结构化数据中存在外界环境噪声干扰的问题。由于原始数据中有大量噪声数据,通过对互补集合经验模态分解方法进行噪声点去除,在此基础上通过改进随机深林模型确定异常点范围,凭借局部敏感哈希算法对结构化数据异常点进行异常度量,可以有效辨识结构化数据中的异常点。实验结果证明,该算法的辨识精准率高、时间短,具有较强的适用性,可以提高海量结构化数据网络的安全性,有效避免数据错误和异常对用户造成影响。