一种极端天气条件下配电网预警系统设计与研究
胡学强, 董伟锋
(南方电网数字电网研究院有限公司, 广东, 广州 510700)
0 引言
如今,现代社会各领域的发展均离不开互联网、电力、水、通信等重要基础设施的正常运转,其中电力设施又是各个环节的基础和根本[1-3]。然而这些基础设施不可避免地面临各种问题和威胁,包括自然灾害(如地震、台风和洪水)和设备老化、退化等。这些挑战增加了配电网基础设施故障的概率,并可能对电网造成前所未有的破坏,如电力塔架倾斜或倒塌、输电线路断裂,甚至形成大规模停电[4-6]。因此,迫切需要建立有效的极端天气下配电网输电线路预警系统,为输电线路的调度、运行、维护和检修提供决策支持。
极端天气事件(如台风)对电网的破坏机理是复杂的,电力设备故障可能由工程施工质量、物理化学环境、极端天气等多种因素造成的。其中一些因素难以量化,因此给原因分析和损伤预测建模带来了挑战。文献[7]设计了一种基于数据分析的电网故障信号预警系统。然而,台风的破坏将导致电网结构的动态变化,数据分析的结果扩展性较差。文献[8]在多时间尺度连锁故障预测模型中考虑台风动态影响线路故障的相关概率,构建连锁故障事故链和台风变化过程的配合关系。然而,使用事故链模型具有较高的计算开销,因此无法用于大规模研究。文献[9]针对110 kV输电线路提出一种同时考虑台风暴雨灾害下的倒塔与断线事故评估方法。然而,台风事件模拟时需要考虑风速概率分布,否则将导致输电线路的失效模型过于简化,从而影响预测结果的可信度。
为此,本文建立了极端天气灾害下输电线路损失预警系统。同时设计了基于随机森林方法、蒙特卡罗方法以及极值Ⅰ型概率分布的输电线路损伤概率计算模型。
1 系统介绍
为了预防和控制极端天气事件对配电网输电线路的破坏,本文构建了配电网极端天气预警系统。系统由3个功能模块组成:信息采集模块、信息处理模块和预警与评估模块。系统详细体系框架如图1所示。
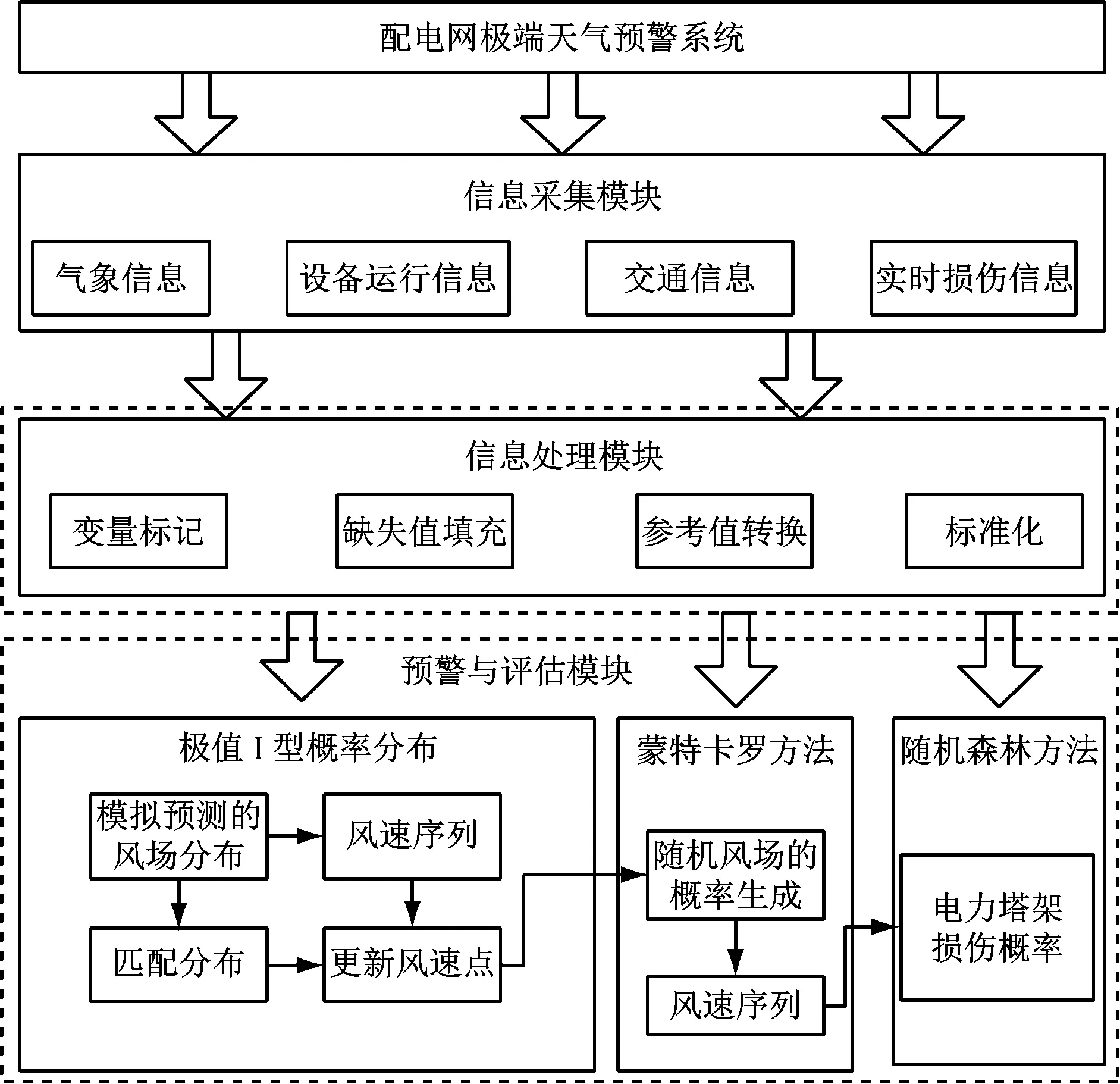
图1 配电网极端天气预警系统框架
1.1 信息采集
信息采集模块能够采集对配电网输电线路损伤预警而言必不可少的信息,涵盖交通信息、气象信息、实时损伤信息、设备运行信息等。虽然输电系统由输电塔、绝缘子、导线和地线等组成,但研究主要考虑配电网输电线路的损坏,包括塔架倾斜和断裂。
1.2 信息处理
信息处理模块包括变量标记、缺失值填充、参考值转换和标准化等操作。其中,变量标记用于标记损坏状态,缺失的值使用中间值填充。进一步,使用参考值转换,将风速和塔架设计风速转换为10 m标准高度。
需注意,风速随高度的变化遵循如下指数规律[10]:
(1)
式(1)中,Vz是高度z处的风速(单位为m/s),V1是高度z1处的风速(单位为m/s),α是表面粗糙度系数。考虑到气象站一般位于开阔平原,其表面粗糙度一般取0.13~0.18。
最后,将所有数据x标准化为:
(2)
式(2)中,x*是标准化特征,x是原始特征,xmin和xmax是原始特征的最小值和最大值。
1.3 预警与评估
评估和预警模块构建设了基于以蒙特卡罗方法[11]、极值I型概率分布[12]、随机森林方法[13](RF)的输电线路损伤概率混合预测模型。更具体地说,采用极值I型概率分布和蒙特卡罗方法来模拟风场。利用RF方法预测了输电线路在各种风场作用下的损伤概率。该混合方法考虑了预测风速的不确定性,实现了基于RF方法每次预测的加权概率输出。
2 混合预测模型
2.1 模型介绍
首先,混合模型采取极值I型概率分布,对预测的相关风场分布进行模拟。风速点间距能够达到1 km×1 km。由于预测风速是时间长达10 min、位于10 m高度处的平均风速,所以能够乘以风速系数,得到高达10 m处的最大风速。风速系数是指从平均风速过渡到瞬时风速的参数,一般情况下界定为10 min间隔内风速和平均风速间的相应比率。如果各风速点的风速分布能够服从极值I型概率分布。
结合距离限制的情况,向各塔匹配风速:
|X1-X2|+|Y1-Y2|≤ξ
(3)
式中,(X1,Y1)是风速的地理坐标,(X2,Y2)是某个发电塔的地理坐标,ξ为任意正实数。如果(X1,Y1)和(X2,Y2)满足式(3),则风速点与该塔匹配,并将塔的坐标作为新的风速点。
其次,以蒙特卡罗方法为基础,完成了随机风场的相应概率生成。在各风速点,按照均匀分布能够随机生成的风速wij达到了M个,其中i(i=1,2,…,N)、j(j=1,2,…,M)分别代表着风速点序列、随机样本序列。而且,能够借助具有良好拟合的极值I型概率分布,将各样本的相关概率计算出来。
最后,在各随机风场中,采取RF方法将电力塔架本身的损伤概率f(xi|wi=wij)计算出来,xi、wi分别代表着风速i点的特征向量、风速分量。按照蒙特卡罗方法,风速点的相关塔架损坏概率和M个预测结果的相应平均值相等。各风速点的相应塔架损坏概率是Pi。
为了使预测结果是可靠的、稳定的,故:
(4)
迭代M时Pi的偏差定义为
(5)
式中,εM是迭代M和M-1之间Pi的偏差,且M>1。本文中的收敛约束定义为|εM|<0.01。
2.2 相似性分析
为了比较不同模型的预测结果的对应数值,本文将下列相似性指标引进:震级相似性、分布相似性、累积相似性和综合相似性。
2.2.1 分布相似性
分布相似性表示预测损害的地理分布与实际损害的接近程度。本文计算预测结果与实际损伤情况之间的分布相似性,分布相似性越大,预测的损伤分布越接近实际情况。具体公式如下:
(6)

2.2.2 震级相似性
损伤概率越高,发生损伤的可能性越大。为了制定准确的防灾减灾战略,有必要设定损失概率的阈值并采取预防措施,即当预测损伤概率大于阈值时,认为发生了损伤;当预测值小于阈值时,不可能发生损伤。
在概率阈值不同的情况下,为了分析实际损伤和预测损伤大小间的相似性,可以如下定义概率阈值Pj下的预测模型i的震级相似性:
(7)
式中,Pj表示j级的概率阈值,M表示实际损伤程度,Mi表示Pj下模型i的预测损伤程度,MSi表示Pj下模型i的损伤程度相似性。MS越大,预测震级越接近实际情况。
2.2.3 累积相似性
为了评估对概率阈值的鲁棒性,累积相似性定义为
(8)
式中,l是概率阈值水平的数量,CSi是模型i的累积相似性。累积相似性反映了模型在不同概率阈值下保持预测精度的能力。CSi越大,模型对概率阈值的鲁棒性越强。
2.2.4 综合相似性
损害预测需要关注损害的分布和程度,以便在不造成低估或高估的情况下做出准确的防灾减灾决策。因此,将综合相似度定义为分布相似度和累积相似度的算术平均值:
(9)
式中,SSi表示模型i的综合相似性,DSi表示模型i的分布相似性。SS值越高,预测的损伤分布和大小越接近实际损伤情况。
3 仿真与分析
3.1 数据采集
预测和测量的风速数据均来自电网部门,其中预测的最大风速数据来自着陆前24小时的预测风速序列。数据集中电力网主要为广东省沿海地区11个城市,分别为惠州、揭阳、潮州、江门、茂名、汕尾、汕头、阳江、中山、湛江以及珠海等。
3.2 信息处理
首先,通过分类变量标记配电网中电力塔的损坏状态。仿真中,损坏状态用1表示,未损坏状态用0表示。此外,本文采用中值插值来填充缺失值。表1所示为仿真中设计的变量及其定义。经过处理后,利用4次台风作用下的损伤信息对模型进行训练。

表1 仿真中设计的变量及其定义
3.3 损伤警告和评估
首先,利用经过处理的四次台风下的损伤信息构建的训练数据集对RF模型进行训练。训练数据集由划分为特征和损伤状态的案例组成。根据信息处理结果,配电网电力塔的损坏状态由分类变量标记,如果塔损坏,分类变量为1,否则为0。数据集中代表损害状态0的案例是从这四次台风的历史记录中随机选择的。然后利用训练数据集拟合RF模型。
各风点的风速都是随机生成的,而且可以按照极值I型概率分布,将其生成率计算出来。可以将RF方法引入产生的风速中,预测损伤概率。重复上述过程,直到概率收敛。
3.4 结果与分析
图2所示为经过150次迭代后,预测损伤概率结果统计图。可以看出,本文所提混合模型预测平均值偏差(AVD)约为0.03,并随着迭代次数的增加而不断波段,且最大不超过0.05。然而,仅只有RF模型情况下预测AVD约为0.07。同理AVD随着迭代次数的增加而不断波段,且最大达到0.1。分析原因,混合预测模型采取蒙特卡罗方法以及极值I型概率分布,对随机风场进行模拟。在风场发生概率是一定的情况下,借助RF法将每个风场下输电线路的相关损伤概率计算出来,将平均损伤效应求出来。相比于混合预测模型,在预测周期内单模型RF方法仅采取最大风速场,但并未考虑各风速点最大风速的概率,所以在具体运用的过程中可能会出现一定局限性。而且,在特定情况下,实测风速获得了丰富的数据,只采取最大风速数据势必会丢失不少有效信息。所以,相比于损伤概率的混合预测模型,采取单一模型中的RF方法,其实际应用价值应该达到更大水平。
进一步,不同方法下4个指标比较结果如表2所示。可以看出,单模型RF法在实测风速下的预测损伤分布最接近实际损伤情况,达到了0.0155。然而在预测风速下只达到了0.0097,这意味着预测风速的不确定性,会在较大程度上影响预测结果。采取混合预测模型后,分布相似性的数值增加到了0.0108,和单模型RF法预测风速的相应结果相比,大致高出了8.62%;预测风速和实际风速下单模型RF方法的震级相似性远低于混合预测模型,表明混合预测模型的预测损伤震级更为准确;混合预测模型本身的累积相似度达到了0.3469,依次比实际风速和预测风速下这两种方式高出了7倍和6倍;最后,混合预测模型的综合相似度最好(0.1785),分别比前两种模型下高约5倍。仿真结果对蒙特卡罗方法以及极值Ⅰ型概率分布模拟台风风场方面的有效性做出了进一步验证。

表2 不同方法下4个指标比较结果
4 总结
本文研究与分析了极端天气事件对配电网造成的损伤概率,提出了一种基于混合模型的配电网极端天气损失预警系统。该系统采用极值I型概率分布和蒙特卡罗方法来模拟风场。利用RF方法预测了输电线路在各种风场作用下的损伤概率。系统考虑了预测风速的不确定性,实现了基于RF方法每次预测的加权概率输出,从而有效提高输电线路损伤概率预测的效果。

