基于超单元法的无轴承尾桨根部动力学等效参数分析

邱志祥, 喻国瑞

(中国直升机设计研究所,江西 景德镇 333001)

0 引言

旋翼动力学分析中的动力学参数即为结构的力学参数,将旋翼简化为梁模型的经典气弹分析方法中,需输入桨叶剖面特性、桨毂剖面特性和操纵线系刚度等参数。

无轴承尾桨柔性梁根部通过金属夹板夹持,在夹持区外侧,袖套与柔性梁通过支撑轴承连接,形成多路传力构型,如图1所示。柔性梁根部变形会影响支撑轴承对袖套的支撑效果,从而影响挥舞二阶模态特性。而挥舞二阶模态通常靠近4Ω,设计不合理会导致共振。传统建模时,假设与金属夹板接触区域的柔性梁简化为刚性梁段,柔性梁根部偏刚硬,无法准确捕捉挥舞二阶模态特性。

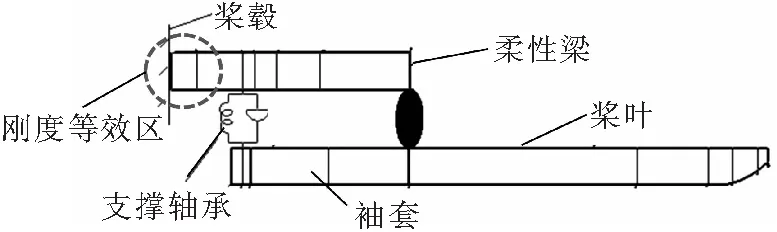
图1 无轴承尾桨动力学建模

针对上述问题,本文利用静力缩聚超单元法计算柔性梁根部夹持区等效动力学参数,分析柔性梁根部不同缩聚长度对尾桨动力学的影响,探究其机理,并给出合适的等效区域方案。尾桨静态动特性试验和旋转动特性试验结果表明,该等效方法计算精度满足工程所需。

1 超单元基本理论推导

超单元法是将各子结构内部自由度缩聚到边界自由度上,然后将子结构的独立边界自由度进行组合求解。常用的超单元法分为三种:静力变换超单元法、定频动力变换超单元法、模态综合超单元法[1-2]。其中,静力变换超单元法强制忽略了内部自由度,会导致高阶振动分析产生较大误差。当关注的频率成分远大于子结构模态频率,静力变换超单元法可大大降低模型分析的复杂度。如图2,假设子结构1是复杂结构,内部多路传力,且包含非线性接触约束,不能直接看成单梁结构。

图2 子结构示意

使用有限元技术,将结构离散,设总共有N个自由度。将N个自由度进行区分,分成子结构1边界上的自由度(下标m)和非边界上的自由度(下标s)。则可以将子结构1的动力学方程写为:

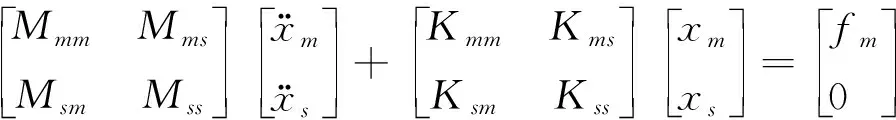
⑴

对上述时域方程做傅里叶变换,可写为频域传递矩阵表达式:

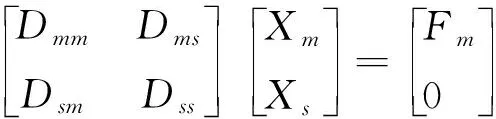
(2)

根据上式有:

DsmXm+DssXs=0

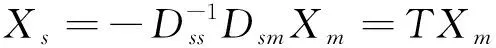
(3)

将(3)带回(2)式,可得

(Dmm+DmsT)Xm=Fm

令

P=Dmm+DmsT

由此可将(1)变换为

PXm=Fm

(4)

上述为超单元法的基本理论,式(4)称为超单元方程,P为超单元动力矩阵。根据该基本理论,完全等效不具有梁特性的子结构1(桨毂),就需要通过桨毂的三维实体,建立有限元模型,再生成2节点超单元梁模型即可。

将超单元方程转换至模态坐标系(Φ为模态振型,ξ为模态坐标),此时子结构动力学方程如下:

ΦT(K-ω2M)Φξ=ΦTFm

(5)

(Kdiag-ω2Mdiag)ξ=Fξ

结构固有频率

最终动力学方程描述如下

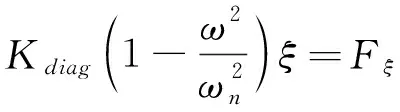
(6)

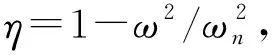
本文所采用的静力缩聚超单元法,是在局部柔性不突出的情况下,子结构最低阶模态固有频率远大于外载激励最高频率,此时P可退化成刚度等效矩阵,因此超单元法的实现流程可转化为对桨毂支臂整体静刚度的等效过程[3]。Sikorsky工程师在开展S-97 CFD-CSD耦合分析结构建模时[4],也利用三维有限元手段,将复杂的桨毂支臂等效为一维梁单元。

2 桨毂支臂三维有限元分析

图3给出了一无轴承尾桨根部柔性梁约束区域示意图,由柔性梁、上下盖板、耐磨板、螺栓组成。离心力通过扁担式柔性梁相互抵消,挥舞、摆振弯矩通过柔性梁传递至盖板。

图3 无轴承尾桨根部结构示意图

2.1 三维有限元建模

分析桨毂支臂传力路径方式,保留其承力主体结构,包括柔性梁、上下盖板、耐磨板和螺栓。

图4给出了柔性梁建模和子区域切分结果。柔性梁是由多种材料铺层组合得到的非均质各向异性结构,为真实模拟其属性,将其按照铺层区域进行弦向、展向切分,使同一区域内铺层信息一致,然后利用复合材料铺层定义该子区域材料属性。

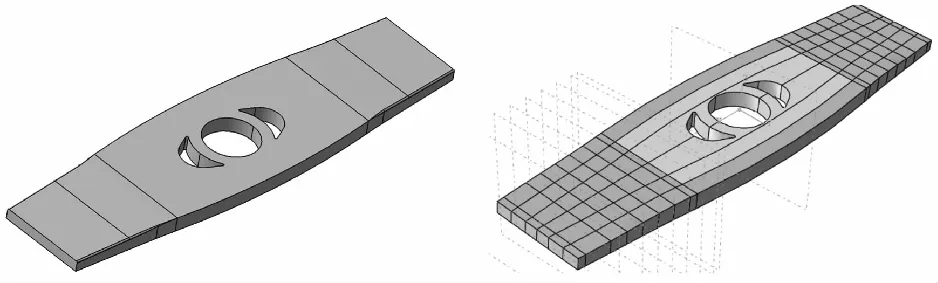
图4 柔性梁建模和子区域切分

模型中包含两大类约束,一是直接Tie,二是设置接触摩擦约束。其中,螺栓端面与内外压板,耐磨板与内外压板接触面设置为Tie;螺栓柱面与盖板,耐磨板与柔性梁耐磨布接触面,柔性梁侧面与内外压板弧形槽面设置为接触摩擦约束。

图5为模型中包含的螺栓。螺栓采用实体模拟,模型中有两种规格的螺栓,包括8个长规格螺栓,4个短规格螺栓。在模型中施加BoltLoad,载荷施加收敛后,设置长度不变条件。

图5 螺栓模型

各柔性梁端面设置RP,作为加载点。固支约束内压板靠近尾减机匣端面。

模型分两步加载:Step1为加载螺栓预紧力,夹紧夹板和柔性梁;Step2为频率分析或静力分析(分别加载挥舞弯矩、摆振弯矩、扭矩)。实际分析时,由于Step1中未约束柔性梁刚体位移,初始未压紧时,模型容易不收敛,因此在两分步中间新增分析步,同时在Step1中增加柔性梁的位移约束条件,保证螺栓加载的收敛性,然后在新增分析步中撤除额外约束条件。

无轴承尾桨具有双路传力布局,柔性梁夹持区域外侧通过支撑轴承和袖套连接,不同长度柔性梁缩聚对尾桨动特性有影响,因此建立不同长度的柔性梁缩聚模型。图6给出了长、短两种柔性梁模型。

图6 无轴承尾桨根部三维有限元模型

2.2 固有频率计算

图7给出了上述长、短柔性梁无轴承尾桨根部三维有限元模型的模态分析结果。

图7 尾桨根部模态分析结果

尾桨动力学设计关注前8阶谐波影响。固支边界条件下,将尾桨根部整体静刚度等效为动力学参数,子结构简化分析误差见表1。

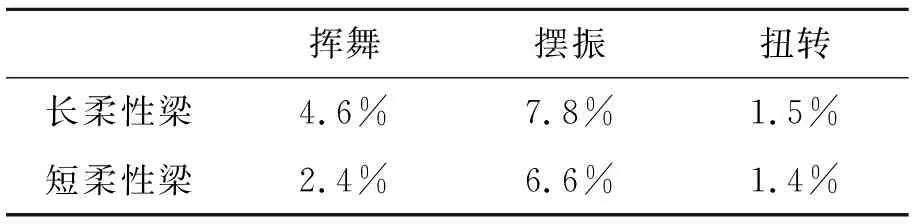
表1 子结构简化分析误差

计算结果表明,子结构简化分析,刚度误差在10%以内。

2.3 静力分析和动力学参数等效

在上述模型的基础上,对桨毂支臂进行静刚度分析。图8给出了长柔性梁模型在不同方向加载下的应力云图。

图8 长柔性梁模型变形云图,加载1000 N·m力矩

计算出柔性梁端面中心点的转角变形,采用静力缩聚超单元法计算出的柔性梁根部等效挥舞刚度、摆振刚度、扭转刚度如表2所示。

表2 加载1000 N·m力矩,静力分析计算转角(rad)和刚度(N·m2)

3 柔性梁等效长度影响分析和旋转动特性试验验证

3.1 不同长度柔性梁等效影响分析

将表2等效刚度带入无轴承尾桨CAMRAD动力学模型,得到各阶模态频率如表3。

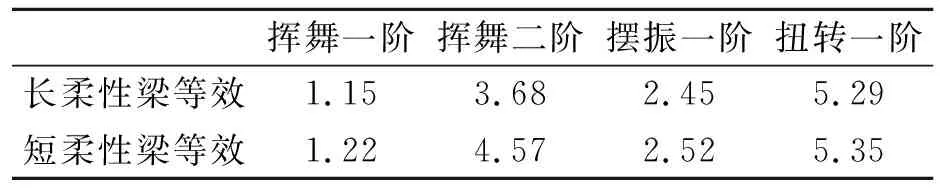
表3 长短柔性梁等效对尾桨频率影响

计算结果表明,不同柔性梁根部缩聚长度对挥舞二阶影响很大。为探究其内部机理,对柔性梁缩聚长度开展影响分析。提取长柔性梁模型中柔性梁中心线的挥舞弯曲变形曲线,曲线斜率即为转角,由转角即可得到等效刚度。图9给出了挥舞变形、转角和挥舞刚度随柔性梁缩聚长度的变化曲线。

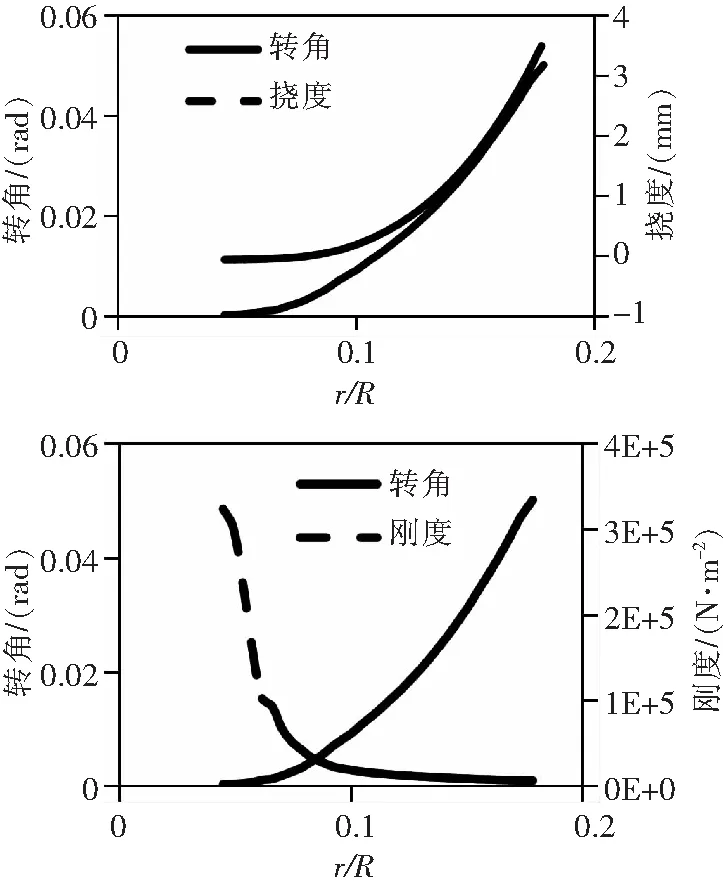
图9 挥舞弯曲变形,挠度、转角、刚度沿展向变化

取不同状态等效刚度,分析挥舞二阶频率,结果如表4和图10。计算结果表明,额定转速、正常支撑轴承参数、挥舞二阶频率随着柔性梁缩聚长度增加呈近似线性降低。不考虑离心力和支撑轴承径向刚度,挥舞二阶绝对值下降,但随柔性梁缩聚长度变化的规律类似。不考虑支撑轴承轴向刚度,柔性梁缩聚长度不影响挥舞二阶频率。

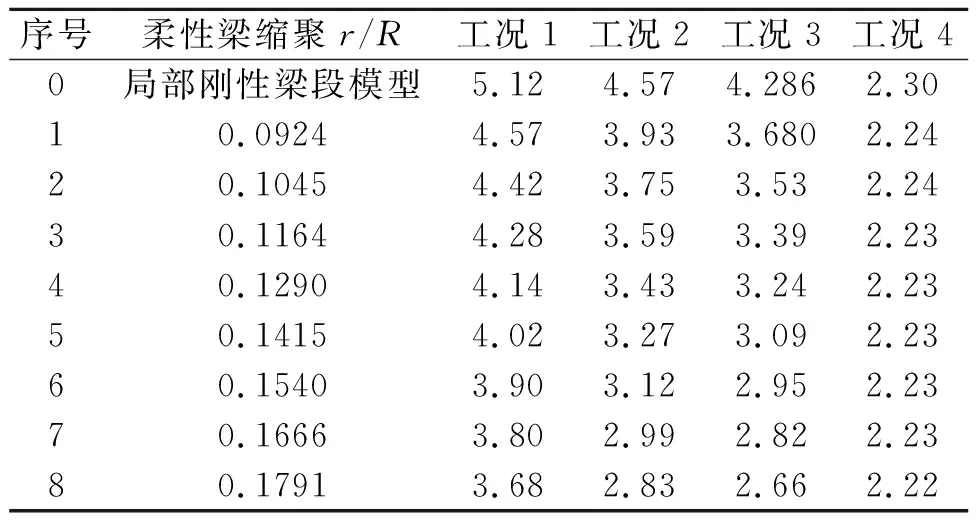
表4 不同状态挥舞二阶频率与额定工作转速之比

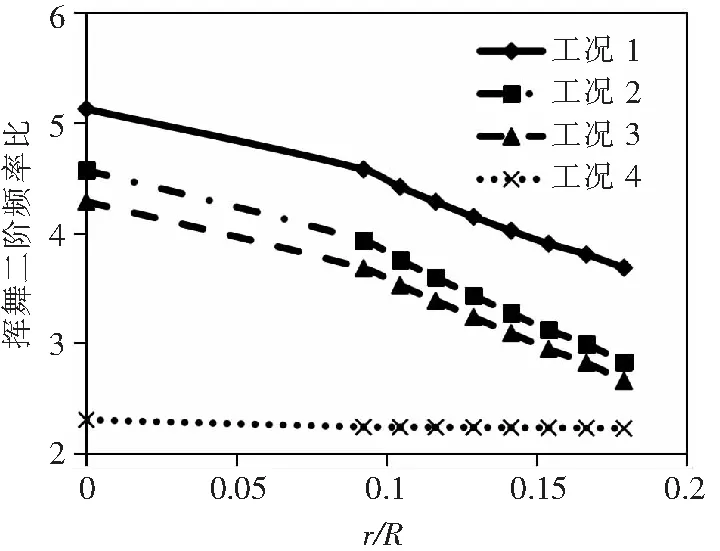
图10 不同工况下的挥舞二阶频率

图11是工况1下不同柔性梁缩聚长度对应的挥舞二阶振型。结果表明,随着柔性梁缩聚长度的增加,袖套根部(支撑轴承到与桨叶融合处)的弯曲变形减弱,意味着袖套弯曲刚度对挥舞二阶贡献降低。这是挥舞二阶频率随柔性梁缩聚长度增加而降低的原因。

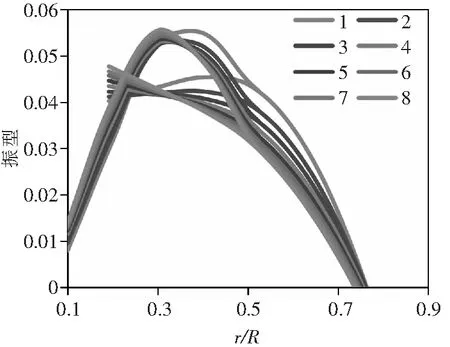
图11 工况1,不同柔性梁缩聚长度,挥舞二阶模态振型

各工况说明如下:工况1—额定转速,正常支撑轴承参数;工况2—0转速,正常支撑轴承参数;工况3—0转速,支撑轴承径向刚度为0;工况4—0转速,支撑轴承径向刚度和轴向刚度均为0。

给定柔性梁缩聚长度为0.1290R,图12给出了不旋转状态下支撑轴承轴向刚度对挥舞二阶的影响。计算表明,支撑轴承刚度对挥舞二阶影响很大,存在一个刚度敏感区,实际设计时应保证刚度在敏感区外,避免挥舞二阶出现较大波动。

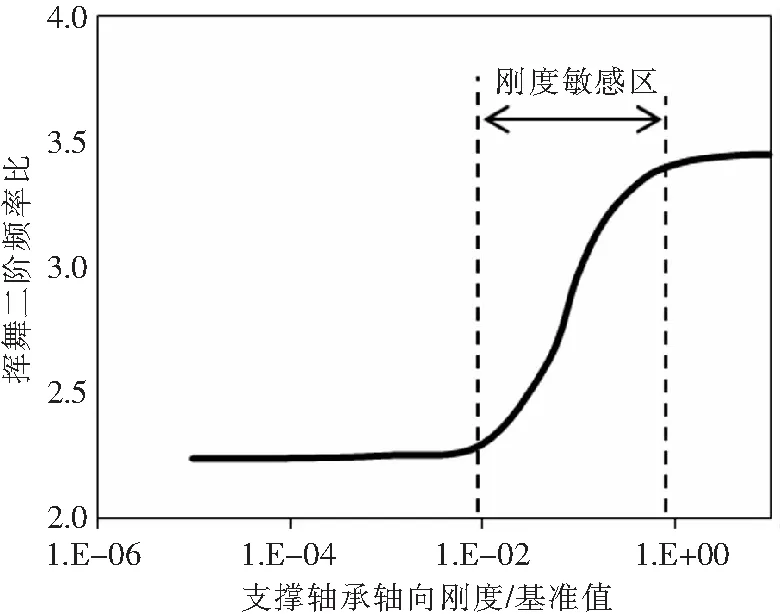
图12 支撑轴承轴向刚度对挥舞二阶频率影响

3.2 试验验证

1)尾桨叶静态动特性试验

将一对尾桨的中央部分通过试验夹具固支在地轨上,模拟实际夹板夹持情况,固支基础尽量刚硬。

表5给出了试验和计算对比。结果表明,考虑柔性梁根部缩聚后,挥舞二阶、摆振一阶计算结果更贴合试验值。计算值仍小于试验值,原因有二:一是桨叶本身制造偏差;二是试验根部约束并不是真正“刚性”条件。

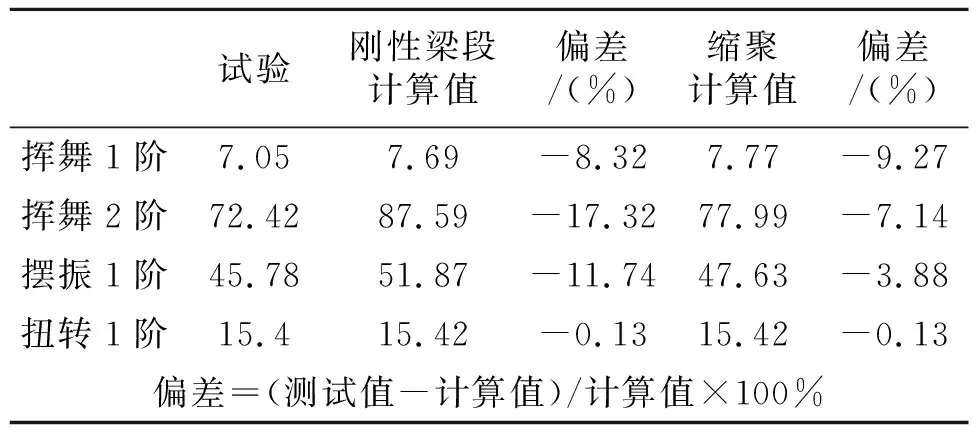
表5 静态动特性试验结果

2)尾桨旋转动特性试验

开展尾桨旋转动特性试验,通过谐波分析方法[5]识别尾桨停车前降转速时域数据。通过识别不同转速共振点,外插得到额定转速下的尾桨叶各阶频率。挥舞二阶和摆振一阶识别结果如表6。

表6 计算值和试验值对比

试验结果与柔性梁夹持区静力缩聚计算结果吻合,说明使用静力缩聚计算无轴承尾桨柔性梁根部动力学参数的有效性。

4 结论

本文利用静力缩聚超单元法计算柔性梁根部夹持区等效动力学参数,分析柔性梁根部不同缩聚长度对尾桨动力学的影响。对于双路传力的无轴承尾桨,柔性梁根部缩聚长度影响袖套在各阶模态中的参与程度,特别是挥舞二阶,需谨慎选取等效区域。计算和试验结果表明,选取夹板夹持区域进行动力学等效,能够较好地满足设计需求。同时,支撑轴承轴向刚度对挥舞二阶频率有较大影响,存在刚度敏感区,设计时需要避开。