电阻应变片应变传递建模与分析

黄飞虎,唐江光,周 鑫

(中国直升机设计研究所 江西 景德镇 333001)

0 引言

电阻应变测试技术由于具有高精度、观测范围广泛和高稳定性等优点,目前已广泛应用于航空航天、交通运输、土木工程和机械工程等众多领域[1-2]。在直升机试验、试飞项目中,电阻应变计是最为常用的应变测试方式。为进一步提高试验、试飞中测试数据的精确性,需要对电阻应变计的应变传递机理进行深入分析与研究。电阻应变计的种类较为多样,其中应用最为广泛的是金属粘贴式电阻应变片。

针对电阻应变片的应变传递机理,国内外学者开展了大量的研究。Stehlin[3]通过建立“基体-胶接层-敏感栅”的一维应变传递模型,推导出电阻应变片敏感栅轴向的应变分布公式;Zike 等[4]利用ABAQUS 软件建立了电阻应变片的有限元模型,通过仿真得到了应变片基底和敏感栅的应变分布,对应变传递的影响参数进行了分析和试验验证;王彪等[5]通过建立“基体—胶接层—基底—敏感栅”的二维应变传递解析计算模型,从理论上分析了金属粘贴式电阻应变计的应变传递机理并得出解析解;许艺青等[6]通过建立电阻应变片的三维简化模型,对不同敏感栅结构进行模拟,揭示其对应变片应变传递的误差影响;Ajovalasit等[7]建立了“基体-敏感栅”的简易应变传递二维模型,分析得到了电阻应变片纵向正应力和切应力分布函数,并计算得出应变片灵敏度系数的近似解。

本文利用ABAQUS软件首次建立电阻应变片“等强度梁(基体)—胶粘层—基底—敏感栅—覆盖层”的三维有限元模型,通过仿真分析得到电阻应变片各结构参数对其应变传递的影响。

1 电阻应变片结构及工作原理

电阻应变片通过胶粘剂粘贴在被测物体(基体)的表面;当基体在外力作用下产生形变时,其应变通过胶粘剂所形成的胶粘层传递到电阻应变片的基底,再从基底传递至敏感栅,使敏感栅栅丝截面面积发生变化,即电阻值相应发生变化;通过测量应变片的电阻值变化即可得出基体的应变。敏感栅是电阻应变片的核心传感元件,一般由康铜、锰铜、铂铱合金等导电性优良的金属材料制成,如图1所示。其中,a表示栅丝的宽度,b表示栅丝之间的间距,c表示栅丝的长度;基底用于保持敏感栅的几何形状,且具有较好的绝缘性以避免基体对敏感栅电阻值造成影响;引出线用于将敏感栅的电信号传递至外界的测量设备中。

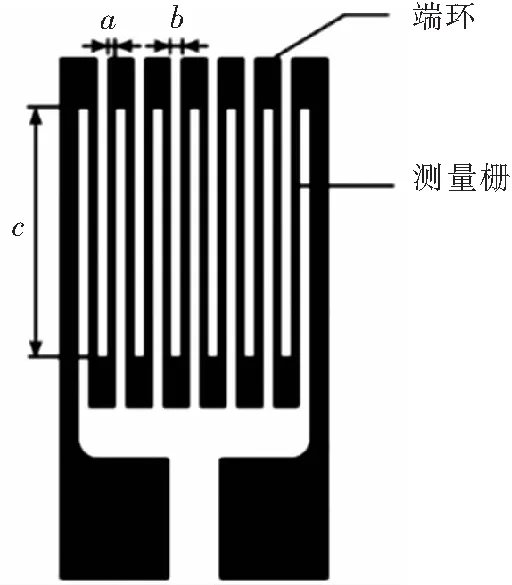
图1 敏感栅模型

电阻应变片在实际应用中,需用胶粘剂将应变片与被测基体粘接在一起,将基体的应变量尽可能精确地传递至应变片。同时,通常需在应变片外表面涂上一层覆盖层,用以防止敏感栅直接受到外界的机械损伤和环境的侵蚀。其基本结构如图2所示。其中,Te表示覆盖层的厚度,Tg表示敏感栅的厚度,Tm表示基底的厚度,Ta表示胶粘层的厚度,Ts表示被测基体的厚度。

图2 应变传递模型剖面图

2 电阻应变片有限元模型建立

本文通过ABAQUS有限元软件建立了“等强度梁(基体)—胶粘层—基底—敏感栅—覆盖层”的有限元模型。为避免产生较大的网格扭曲问题,所有部件均采用细网格剖分的线性减缩积分单元C3D8R,不同层之间均采用绑定约束(tie)。为提高有限元仿真结果的准确性,同时尽可能地减少模型的计算量,在网格划分时对基体、敏感栅进行了局部网格的加密。具体有限元模型如图3所示。各部件具体尺寸及材料参数如表1所示。

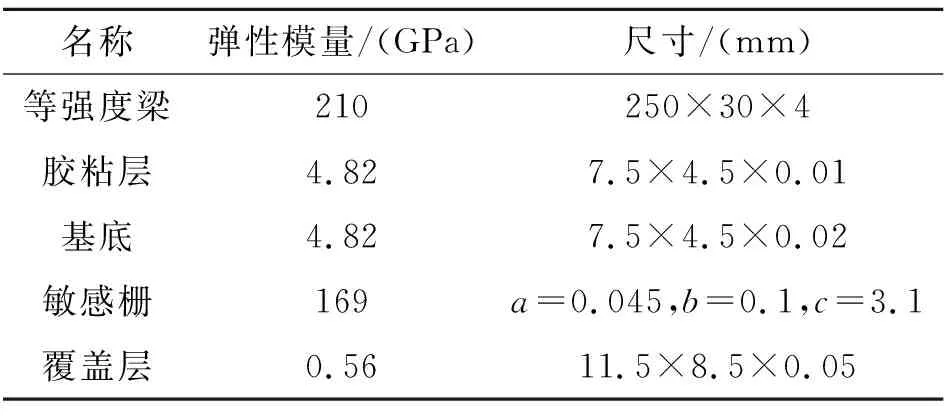
表1 各部件尺寸及材料参数

图3 有限元模型

将等强度梁左端上下表面全约束,并在右端焦点处施加9 N的集中载荷。其受力简图如图4所示。

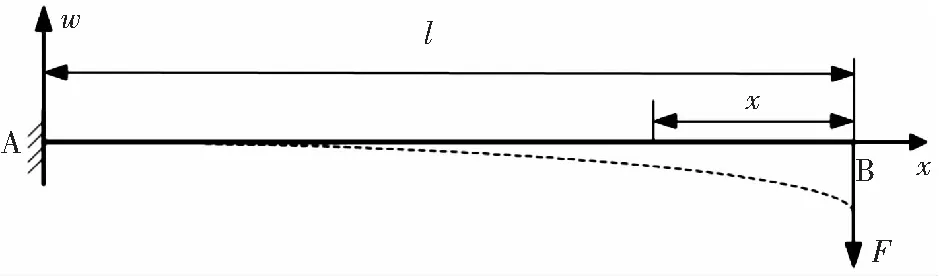
图4 等强度梁受力分析模型

根据梁的挠曲轴微分方程及该模型的边界条件可以求出该模型在x点处的挠度和应变分别为:

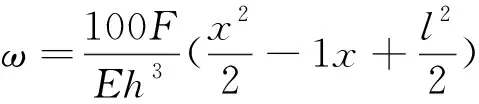
(1)

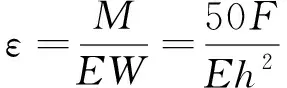
(2)

式中,ω表示等强度梁的挠度,F表示等强度梁焦点处所受集中载荷,E表示等强度梁的弹性模量,h表示等强度梁的厚度,x表示x点到B点间的距离,l表示梁的全长,M表示x点处所受弯矩,W表示x点处的抗弯截面系数。

故可求出等强度梁B点处的挠度为2.09 mm,等强度梁上下表面三角区x方向平均应变为1.33×10-4。

通过ABAQUS有限元软件仿真得到未粘贴应变片时等强度梁模型挠度云图与x方向应变云图分别如图5、图6所示。

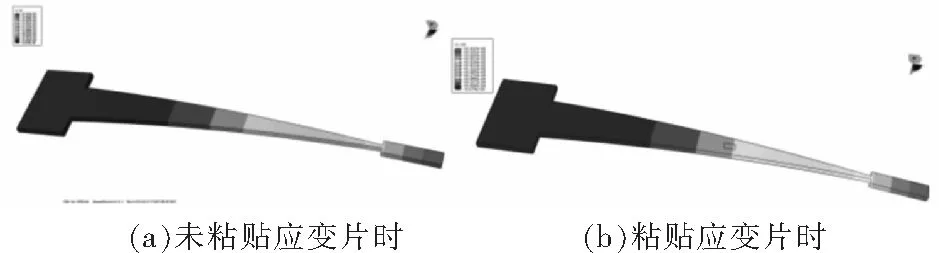
图5 未粘应变片时的挠度云图

图6 未粘应变片时的E11应变云图

由图可知,未粘贴应变片时,等强度梁焦点处的挠度为2.06 mm,等强度梁上下表面三角区x方向平均应变为1.20×10-4。仿真结果与理论计算值基本一致,表明了该等强度梁有限元模型的有效性。粘贴应变片时,等强度梁焦点处的挠度为2.05 mm,等强度梁上下表面三角区x方向平均应变为1.19×10-4,相比于未粘贴应变片时的值基本没有改变,表明应变片的粘贴对基体的变形几乎无影响。

已知电阻式应变片整体E11(x方向)应变云图如图7所示。

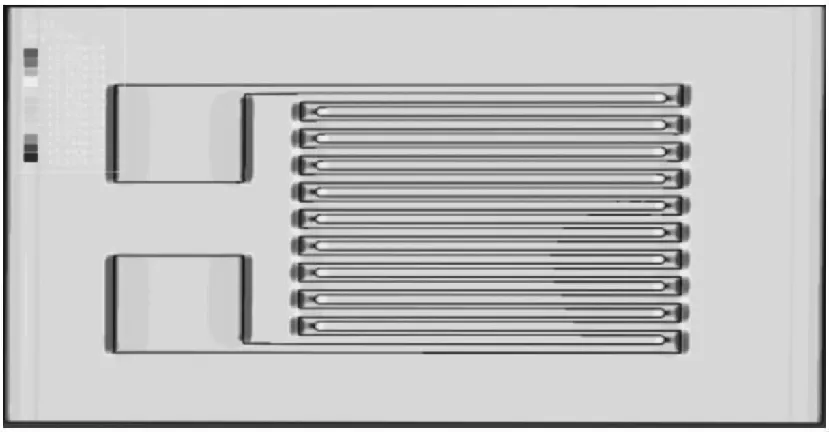
图7 电阻式应变片E11应变云图

提取应变片path路径上所有节点的应变值绘制应变片的应变分布曲线如图8所示。

图8 E11应变分布曲线

图中,蓝色曲线(实线)为应变片基底应变分布曲线,红色曲线(虚线)为应变片敏感栅应变分布曲线。区域a为被测结构表面与基底之间的应变过渡区域,区域b为基底与敏感栅之间的应变过渡区域。由于应变过渡区a的存在,在制造电阻应变计的时候通常使基底尺寸远大于敏感栅尺寸,以保证敏感栅丝不受粘贴过渡区的影响。在应变过渡区b中,敏感栅最外端的应变几乎为0,越靠近应变片中心位置的应变越大,直至等于被测基体的实际应变。应变过渡区b的存在,使得应变片敏感栅整体长度上的平均应变不可能100%等于被测基体的实际应变,即电阻式应变片的平均应变传递率(敏感栅整体长度平均应变/被测基体实际应变)只能无限趋近于1,且该传递率随着敏感栅长度的增大而增大。

3 各参数对应变传递的影响

由于电阻式应变片在实际应用中,需要通过胶粘剂将其粘贴至被测基体表面,被测基体的应变通过基体与胶粘剂间的剪切力传递至胶粘层;之后通过胶粘层与应变片基底间的剪切力传递至基底;最后通过基底与敏感栅间的剪切力传递至敏感栅。因此,需考虑各个结构的参数对应变片应变传递的影响。

3.1 基体弹性模量对应变传递的影响

等强度梁(基体)几何尺寸和胶粘层、基底、敏感栅、覆盖层物理参数保持不变,仅改变基体的弹性模量E,分别为0.21 GPa、2.1 GPa、21 GPa、210 GPa和2100 GPa时,敏感栅应变分布曲线如图9所示,相应的应变传递率变化曲线如图10所示。

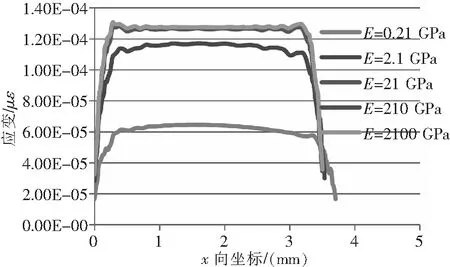
图9 应变分布曲线

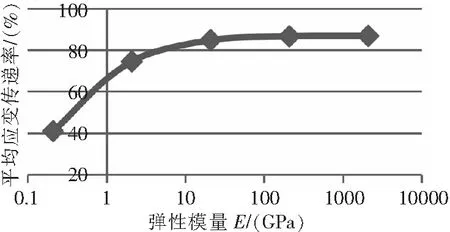
图10 应变传递率变化曲线

由图9、图10可知,基体弹性模量越大,敏感栅中间最大应变点的应变值越大,中间端的应变分布越均匀。平均应变传递率随弹性模量的增大而增大。增大幅度在弹性模量0.21 GPa～2.1 GPa区间内最为明显,在弹性模量210 GPa～2100 GPa区间内几乎不变。该特性表明应变片在测量弹性模量越大的基体时所测出的平均应变值越接近真实值;基体弹性模量越小,测量值越不准确。

由于电阻应变计的灵敏度系数一般通过在专门灵敏度系数检定装置上标定得到,因此为保证实际测量中灵敏度系数的准确性,实际被测基体弹性模量应当尽量与标定试验中的基体弹性模量保持一致。

3.2 胶粘层弹性模量对应变传递的影响

胶粘层几何尺寸和等强度梁(基体)、基底、敏感栅、覆盖层物理参数保持不变,仅改变胶粘层的弹性模量E,分别为0.01 GPa、0.1 GPa、4.82 GPa、10 GPa和100 GPa时,敏感栅应变分布曲线如图11所示,相应的应变传递率变化曲线如图12所示。

图11 应变分布曲线

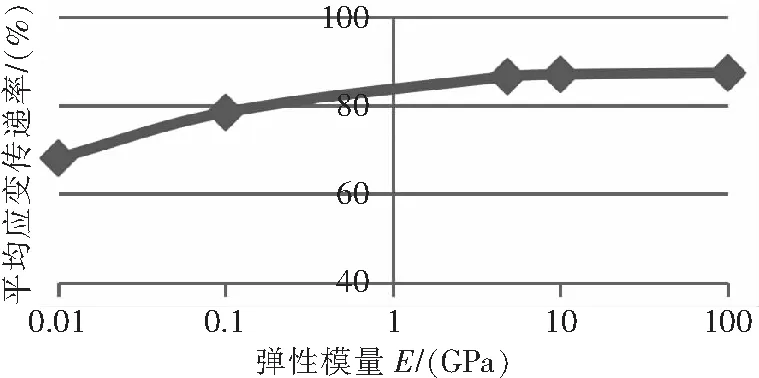
图12 应变传递率变化曲线

由图11、图12可知,胶粘层弹性模量越大,敏感栅中间最大应变点的应变值越大,中间端的应变分布越均匀。平均应变传递率随弹性模量的增大而增大,幅度在弹性模量0.01 GPa～0.1 GPa区间内最为明显,在弹性模量4.82 GPa～100 GPa区间内几乎不变。该特性表明在选择胶粘剂时应当尽量避免使用低弹性模量的胶粘剂,且胶粘剂高的弹性模量对平均应变传递率的影响不大,其值在4.82 GPa左右即可满足测量需求。目前常用的α-氰基丙烯酸酯类胶粘剂(502快干胶)固化后弹性模量在2 GPa～5 GPa之间。

3.3 基底弹性模量对应变传递的影响

基底几何尺寸和等强度梁(基体)、胶粘层、敏感栅、覆盖层物理参数保持不变,仅改变基底的弹性模量E,分别为0.01 GPa、0.1 GPa、4.82 GPa、20 GPa和100 GPa时,敏感栅应变分布曲线如图13所示,相应的应变传递率变化曲线如图14所示。

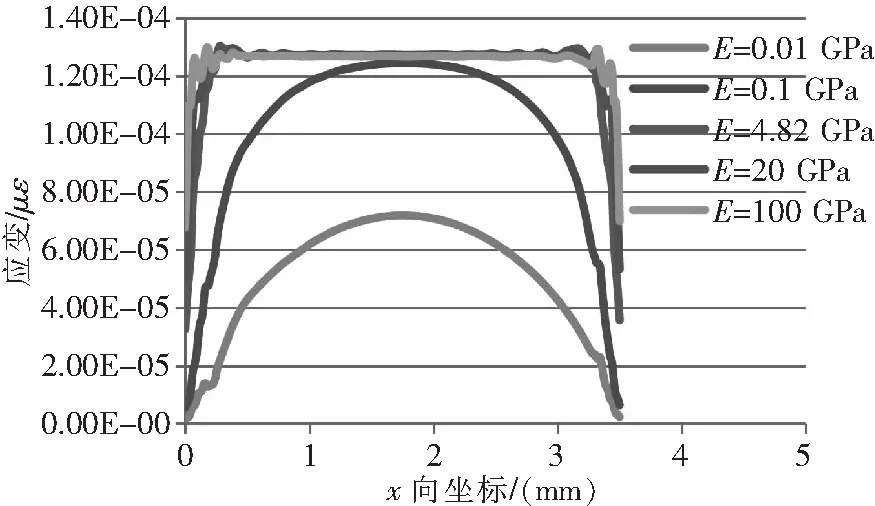
图13 应变分布曲线

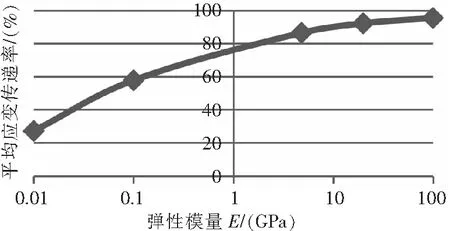
图14 应变传递率变化曲线

由图13、图14可知,基底弹性模量越大,敏感栅中间最大应变点的应变值越大,中间端的应变分布越均匀。平均应变传递率随弹性模量的增大而增大,幅度在弹性模量0.01 GPa～0.1 GPa区间内最为明显,在弹性模量4.82 GPa～100 GPa区间内仍有一定程度的增大。该特性表明应变片设计制造过程中,在保证应变片基底较高绝缘性和可塑性的同时应当尽量选择弹性模量较大的材料。

3.4 敏感栅弹性模量对应变传递的影响

敏感栅几何尺寸和等强度梁(基体)、胶粘层、基底、覆盖层物理参数保持不变,仅改变敏感栅的弹性模量E,分别为10 GPa、100 GPa、169 GPa和210 GPa时,敏感栅应变分布曲线如图15所示,相应的应变传递率变化曲线如图16所示。

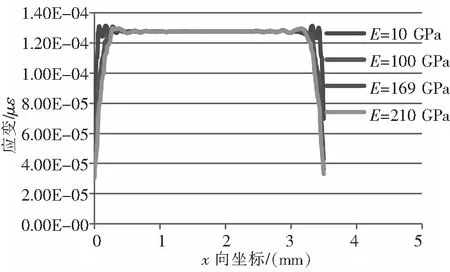
图15 应变分布曲线

图16 应变传递率变化曲线

由图15、图16可知,敏感栅中间最大应变点的应变值和中间端的应变分布几乎不随敏感栅弹性模量的改变而改变。平均应变传递率随弹性模量的增大而减小,但幅度在弹性模量10 GPa～210 GPa区间内均没有太大的变化。

3.5 覆盖层弹性模量对应变传递的影响

其他参数保持不变,仅改变敏感栅的弹性模量E,分别为0.56 GPa、5.6 GPa、56 GPa和560 GPa。此外,由于短期试验中常常存在不涂抹覆盖层以缩短试验周期的现象,故本文同时对有无覆盖层对应变传递的影响进行研究。敏感栅应变分布曲线如图17所示,相应的应变传递率变化曲线如图18所示。

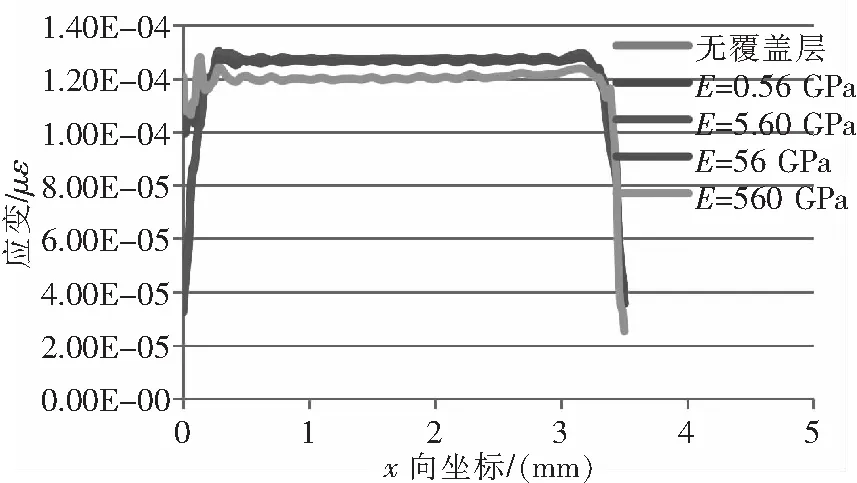
图17 应变分布曲线

图18 应变传递率变化曲线

由图17、图18可知,覆盖层弹性模量越大,敏感栅中间最大应变点的应变值越小,中间端的应变分布越不均匀。平均应变传递率随弹性模量的增大而减小,但幅度在弹性模量0.56 GPa～56 GPa区间内变化较小。目前覆盖层常用的南大705硅橡胶固化后的邵氏硬度为15 HA,弹性模量约为0.56 GPa。通过对无覆盖层和覆盖层弹性模量E=0.56 GPa对应的敏感栅应变分布曲线进行对比可知,两条应变分布曲线基本一致,即覆盖层的有无对应变片的测量几乎没有影响。在不考虑防潮防尘的短期试验中,应变片粘贴时可以不涂抹覆盖层以节约试验时间。

3.6 胶粘层厚度对应变传递的影响

等强度梁(基体)、基底、敏感栅和覆盖层物理参数保持不变,仅改变胶粘层厚度,分别为0.001 mm、0.003 mm、0.01 mm和0.03 mm时,敏感栅应变分布曲线如图19所示,相应的应变传递率变化曲线如图20所示。

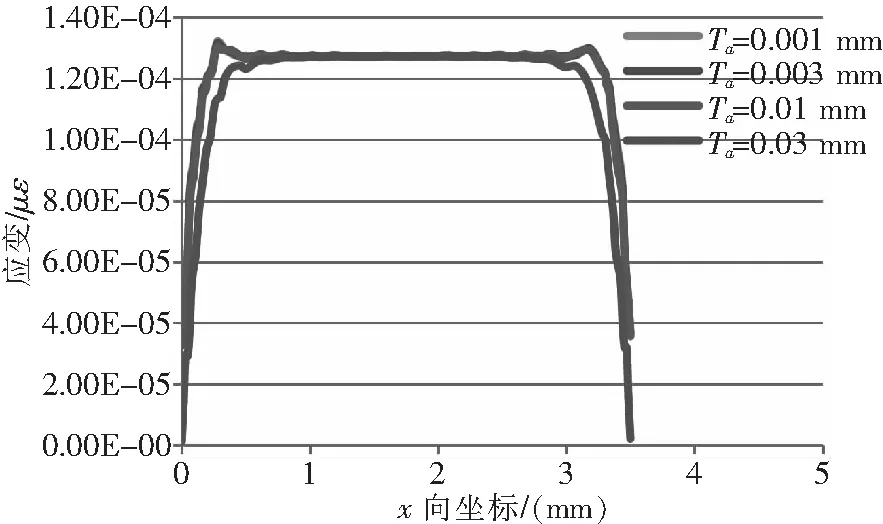
图19 应变分布曲线

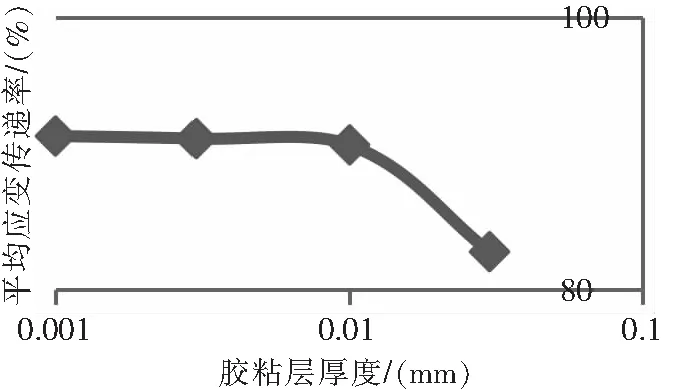
图20 应变传递率变化曲线

由图19、图20可知,敏感栅中间最大应变点的应变值和中间端的应变分布几乎不随胶粘层厚度的变化而变化,但应变过渡区b宽度明显变大。平均应变传递率随胶粘层厚度的增大而减小,但幅度在厚度0.001 mm ～0.01 mm区间内变化较小,在厚度0.01 mm ～0.03 mm区间内变化较大。因此,为保证应变片的测量精准度,在粘贴应变片时应保证胶粘层的厚度不大于0.01 mm。

3.7 基底厚度对应变传递的影响

等强度梁(基体)、胶粘层、敏感栅和覆盖层物理参数保持不变,仅改变基底厚度,分别为0.002 mm、0.006 mm、0.02 mm、0.06 mm和0.2 mm时,敏感栅E11应变分布曲线如图21所示,相应的应变传递率变化曲线如图22所示。

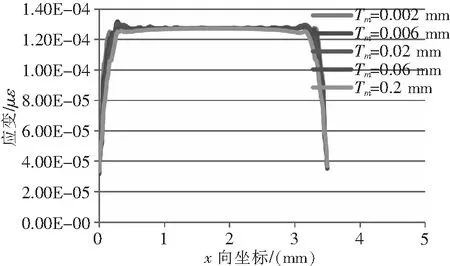
图21 应变分布曲线

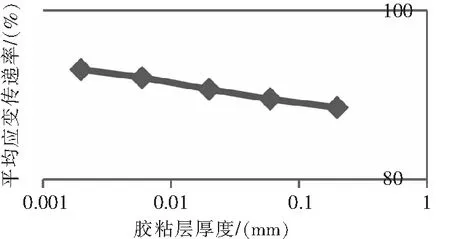
图22 应变传递率变化曲线

由图21、图22可知,随基底厚度增大,敏感栅中间最大应变点的应变值和中间端的应变分布几乎不变,但应变过渡区b宽度明显变大。平均应变传递率随基底厚度的增大而减小,变化幅度在厚度0.002 mm ～0.2 mm区间内基本一致。因此,为保证应变片的测量精准度,在该区间内的基底厚度越小越好。

3.8 敏感栅厚度对应变传递的影响

等强度梁(基体)、胶粘层、基底和覆盖层物理参数保持不变,仅改变敏感栅厚度,分别为0.0001 mm、0.001 mm、0.003 mm、0.006 mm和0.03 mm时,敏感栅E11应变分布曲线如图23所示,相应的应变传递率变化曲线如图24所示。

图23 应变分布曲线

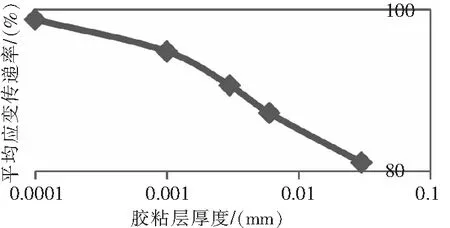
图24 应变传递率变化曲线

由图23、图24可知,敏感栅中间最大应变点的应变值和中间端的应变分布几乎不随敏感栅厚度的变化而变化,但应变过渡区b宽度明显变大。平均应变传递率随敏感栅厚度的增大而减小,变化幅度在厚度0.0001 mm ～0.03 mm区间内基本一致。因此,为保证应变片的测量精准度,在该区间内的敏感栅厚度越小越好。

3.9 敏感栅泊松比对应变传递的影响

敏感栅几何尺寸、等强度梁(基体)、胶粘层、基底和覆盖层物理参数保持不变,仅改变敏感栅泊松比,分别为0.1、0.2、0.3、0.4和0.5时,敏感栅E11应变分布曲线如图25所示,敏感栅E22(应变片横向)应变分布曲线如图26所示。

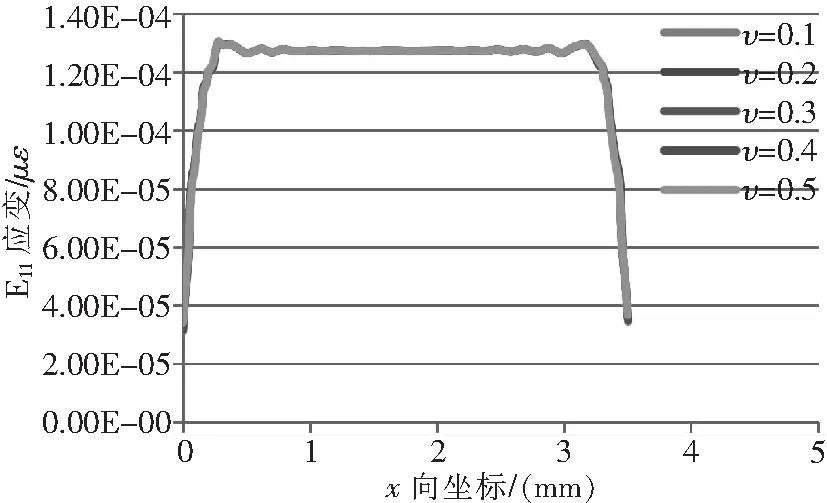
图25 应变分布曲线

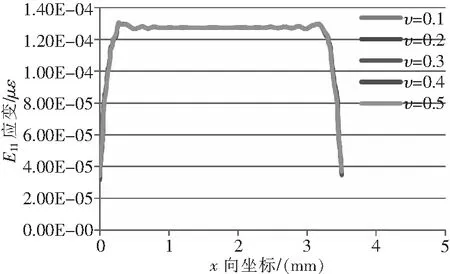
图26 应变分布曲线

由图25、图26可知,随敏感栅泊松比增大,敏感栅E11应变的中间最大应变点的应变值、中间端的应变分布和应变过渡区均几乎不变;敏感栅E22应变的中间最大应变点的应变值随着泊松比的增大而减小,应变过渡区宽度基本不变。由此可知,敏感栅材料的泊松比越大,其单位载荷下的截面收缩率越大,即电阻变化率越大,灵敏度越高。但敏感栅端部弯曲部分的横向效应也会随着泊松比的增大而进一步导致敏感栅灵敏度的降低[8],因此需适当选择敏感栅材料的泊松比。

4 结论

1)利用ABAQUS软件建立了“等强度梁(基体)—胶粘层—基底—敏感栅—覆盖层”的电阻式应变片有限元模型,通过对该模型三角区E11应变和焦点处挠度的有限元仿真和理论计算对比,初步验证了模型的有效性。

2)通过仿真得到应变片在具体参数下的应变云图及其应变分布曲线,由该曲线可知应变片敏感栅端部与基底间存在应变过渡区,使得应变片敏感栅平均应变不等于被测基体的实际应变。

3)本文分析研究了各部件弹性模量、厚度、覆盖层有无和敏感栅泊松比对应变片应变分布和平均应变传递率的影响。结果表明,基体、胶粘层和基底弹性模量越大,敏感栅和覆盖层弹性模量越小,胶粘层、基底和敏感栅厚度越小,则应变过渡区宽度越小,平均应变传递率越大。此外,敏感栅泊松比既会影响栅丝的电阻变化率,也会影响端部的横向效应,故存在一个最优值;覆盖层的有无对应变片的应变传递几乎无影响,故在实际应变片粘贴过程中可适时删除此项工艺。

4)针对大应变试验中应变片测不准及栅丝断裂问题,可以通过减小胶粘层和基底弹性模量来降低应变传递率,并尽量确保试验中被测基体弹性模量与应变片灵敏度标定试验中基体弹性模量保持一致。同时,可通过减小敏感栅泊松比的方式降低单位应变下栅丝的截面收缩率,从而有效缓解栅丝断裂问题。