一种用于激光跟踪仪的无纹波最少拍控制器＊

毛帅，刁晓飞，王先强，周辉，李安琪

（1.山东理工大学电气与电子工程学院，山东 淄博 255000；2.中国计量科学研究院几何量计量科学研究所，北京 100029；3.中电装备山东电子有限公司，山东 济南 250000）

激光跟踪仪具有速度快、精度高和测量范围大的特点，在航天航空、汽车制造、电子工业及大尺寸计量等领域具有广泛的应用[1]。激光跟踪仪是光机电一体化仪器设备，其运动跟踪主要依靠俯仰和水平旋转的2 部永磁伺服电机（PMSM）来实现。PMSM 伺服系统一般为位置环、速度环和电流环三闭环控制结构[2-3]，如图1 所示。目前，PMSM 控制结构中的电流环和速度环工程实现时都采用PⅠ控制器，而位置环采用P 调节器。这种工程的实现具有简易可行和强鲁棒性等特点[4-5]。但是激光跟踪仪需要有非常好的跟踪精度，不然会引起跟踪测量中断并干涉测量误差，常规的PMSM 三闭环控制系统不是完全适合激光跟踪仪的应用要求，所以需要设计跟踪精度更高、跟踪效果更好的PMSM 控制系统。

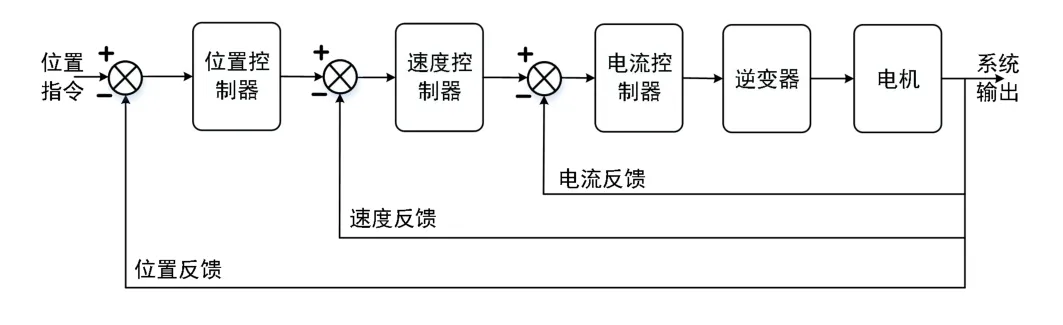
图1 PMSM 三闭环控制系统结构图

本文中，笔者在使用常规电流环和速度环PⅠ控制器的基础上，设计了一种能实现控制系统无纹波最少拍状态的位置环控制器，从而改进常规的PMSM 三闭环控制系统，满足激光跟踪仪高精度和快速跟踪的要求。

1 无纹波最少拍控制机理

具有数字控制器的离散控制系统如图2 所示。图2中，R（z）为参考输入，E1（z）为系统误差信号，D（z）为数字控制器，E2（z）为E1（z）经D（z）后的误差信号，G（z）为离散系统其他功能模块传递函数整合在一起的传递函数，C（z）为实际输出。

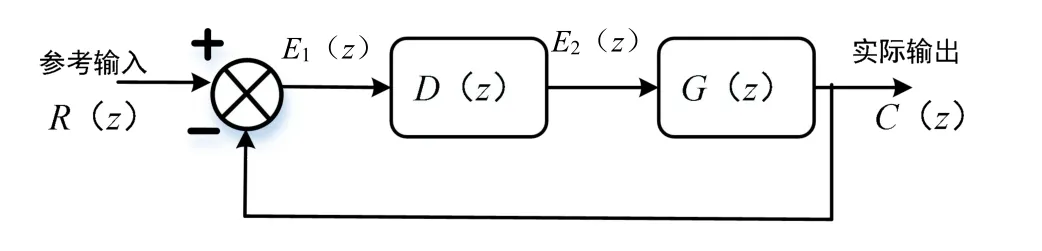
图2 具有数字控制器的离散控制系统

该离散系统的闭环传递函数和误差传递函数分别为：

显然，Φ（z）+Φe（z）=1，由式（1）和式（2）可求出数字控制器D（z），公式如下：

假设输入为斜坡函数，则输入R（z）可表示为：

式中：Kslope为斜坡函数斜率的数值；T为采样时间的数值。

由此可得误差信号E1（z）和E2（z），公式为：

一个采样周期称为一拍，经过最少拍使误差信号E1（z）为0，实现系统的无稳态误差输出，则此时的离散系统称为最少拍系统；在最少拍系统基础上，如果经过有限拍后，使误差信号E2（z）为固定值，将无纹波输入到G（z），则此时的离散系统称为无纹波最少拍系统。将E1（z）和E2（z）表示为z-1的多项表达式，即：

要实现离散系统的无纹波最少拍化，就是使式（7）和式（8）中的k1拍时刻及其以后所有时刻的e1为0，表明此刻跟踪上了目标位移；并且使公式中的k2拍时刻及其以后所有时刻的e2为固定值，表明此刻没有纹波，从而可避免纹波对系统造成损耗。

PMSM 控制一般采用最大转矩电流比的控制策略：d轴电流Id为0，主要控制q轴电流Iq，当d轴电流确定后，电磁转矩与q轴电流呈正比关系，从而实现电机的调速控制。根据PMSM 的电流方程、转矩方程和运动方程，便可建立PMSM 控制系统的速度环和电流环仿真模型，如图3 所示。图3 中，Lq为q轴电感分量，s 为s 域算子，R为定子电阻，J为转动惯量，B为阻尼系数，转矩系数KL为1.5 倍的磁极对数Pn，总延迟时间Tc在控制中近似表示为一阶惯性环节，30/π为速度单位rad/s 转换为r/min 的单位换算系数。因为跟踪仪的负载是固定不变且质心对称的，所以运动方程不用考虑负载转矩；并且使用有功阻尼方式对速度环进行PⅠ调节[6-7]，所以在速度环中添加了有功阻尼系数Ba。

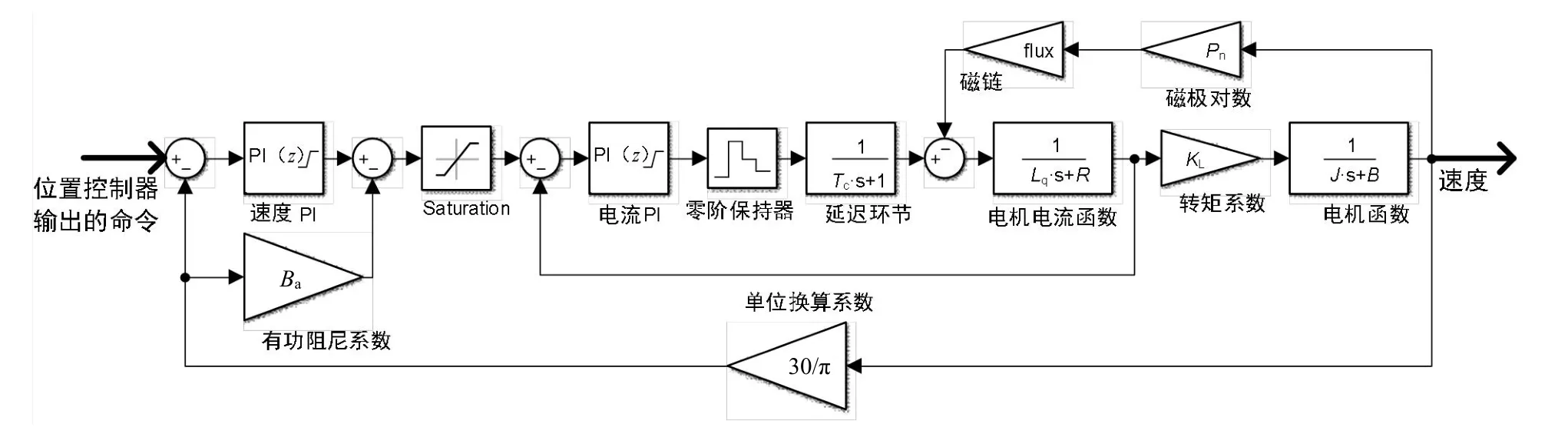
图3 PMSM 控制系统的速度环和电流环仿真模型

PMSM 控制系统的速度环和电流环都是采用PⅠ调节方式，因此，两环整合在一起的闭环传递函数可以等效为一阶低通滤波器（即使整合在一起的闭环传递函数不为一阶低通滤波器形式，通过调整两环的PⅠ调节器，也可将其变为一阶低通滤波器形式），该一阶低通滤波器离散域（z变换）形式为：

式中：A为放大系数；a为负的极点值。

一阶低通滤波器形式的响应类似过阻尼响应，响应中没有振荡响应变化。从激光跟踪仪的实际测量角度来说，因为电机运动控制过程中的跟踪的抖动振荡会使干涉光斑重叠度变小或使光斑位置在其精确测量区域外，这会导致激光跟踪仪中断其测量并使位移测量误差变大，因此激光跟踪仪的运动控制只允许有微小振荡，所以速度环和电流环整合在一起的闭环传递函数最适合整定为一阶低通滤波器形式。由此可得PMSM 离散控制系统整体模型，如图4 所示。

图4 PMSM 离散控制系统

对比图4 和图2，可看出位置环控制器P（z）就是图2 中的D（z），Gvi（z）、I（z）就是图2 中的G（z），其中I（z）为积分环节，I（z）=（30/π）/（1－z-1），通过设计P（z）就能实现PMSM 无纹波最少拍控制。

激光跟踪仪的跟踪的任意运动轨迹可看成许多非常微小段线性位移的集合，在某时刻一个微小线性段中轨迹速度不变（该速度为轨迹在此刻对应切线方向速度），在不同时刻不同运动速度的微小线段可以看成是不同斜率Kslope的斜坡函数。所设计的无纹波最少拍控制系统就是要实现在该线性段对应的采样时间内使PMSM 跟踪上实际轨迹位置点。取PMSM 离散控制系统的闭环传递函数和误差传递函数，分别为：

由式（10）、式（11）和式（3）可求出对应的位置环控制器P（z），即：

此时E1（z）和E2（z）为：

由式（13）可看出控制系统第二拍后值为0，即表示跟踪上了目标；由式（14）可看出控制系统第三拍后变成固定值，即表示此时控制系统无纹波。

2 仿真实验

这里使用图4 模型进行跟踪仿真。其中，Lq=12 mH，R=0.958 Ω，J=0.003 kg·m2，B=0.008 N·s/m，KL=6，Pn=4，Tc=0.5 ms，Ba=0.013，另外磁链值为0.182 7 Wb，电流环的比例调节系数取31.68，积分调节系数取1 053.8，速度环的比例调节系数取0.058 8，积分调节系数取2.66。

在仿真之前要先确定输入的斜坡函数最大斜率（即确定最大跟踪速度）。如果输入为单位斜坡函数，对应激光跟踪仪跟踪速度为360°/s，对应的在1 m 处的跟踪线速度约为6.3 m/s，在10 m 处跟踪线速度约为63 m/s，该速度已经可以满足现有的测量跟踪场景。所以，这里确定仿真时所输入斜坡函数的最大斜率为1。

图5 为3 种斜率输入时对应的输出响应及纹波情况（采样时间为0.001 s）。由图5 可看出，当第二拍时输出跟上了输入响应，并在第三拍后纹波消失，这与第二小节推导的最终结论一致。在跟踪仪测量时，PMSM 旋转多少角度（位置命令）是由光斑位置探测器测量决定的，光斑位置探测器采样时间TPSD内可认为是速度不变的微小段线性位移。

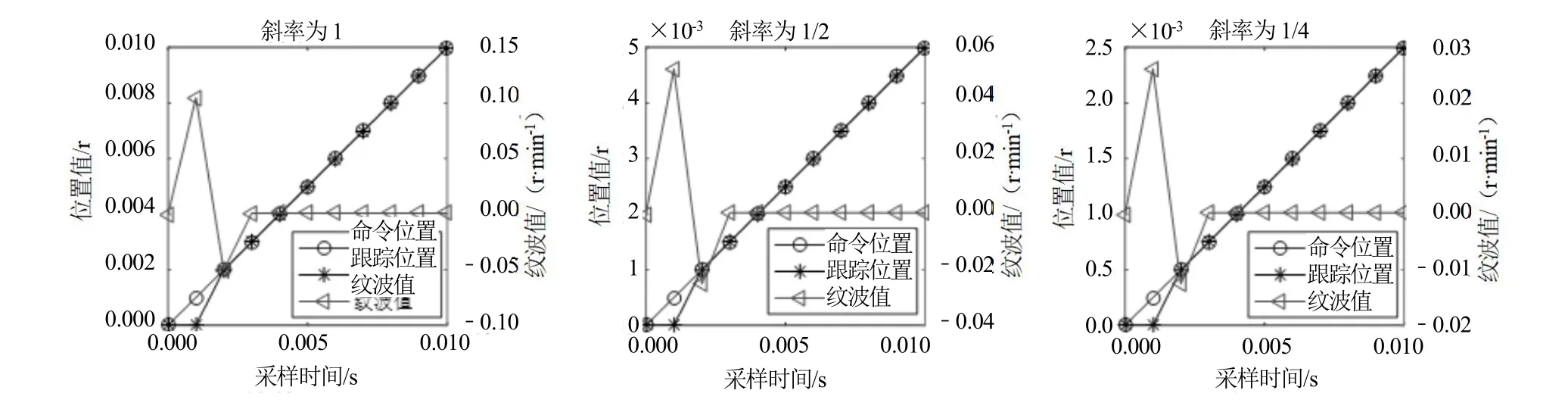
图5 3 种斜率输入时对应的输出响应及纹波情况

另外，由图5 可知，只要光斑位置探测器的采样时间TPSD大于等于3 倍的控制系统采样时间Tcon，就可以实现控制系统的无纹波最少拍状态。

图6 为单位频率正弦轨迹跟踪效果图。由图6 可看出，轨迹跟踪效果很好，在采样点（采样时间TPSD=0.003 s）上完全地跟踪上了命令。目前，PMSM控制系统中的位置环一般为比例调节器，如果将图4模型的P（z）（公式（12））换成比例调节器，其3 种不同比例值对应的单位频率正弦轨迹跟踪效果如图7 所示。相较图6，图7 的跟踪效果明显较差，当比例较小时会存在延迟跟踪现象，比例较大时会出现超量和欠量跟踪交替出现的振荡式跟踪效果。如果是一般的PMSM 控制应用，小幅度振荡式的跟踪现象是可以接受的，但是在激光跟踪仪应用中，这种情况极易引起跟踪测量中断并干涉测量误差。

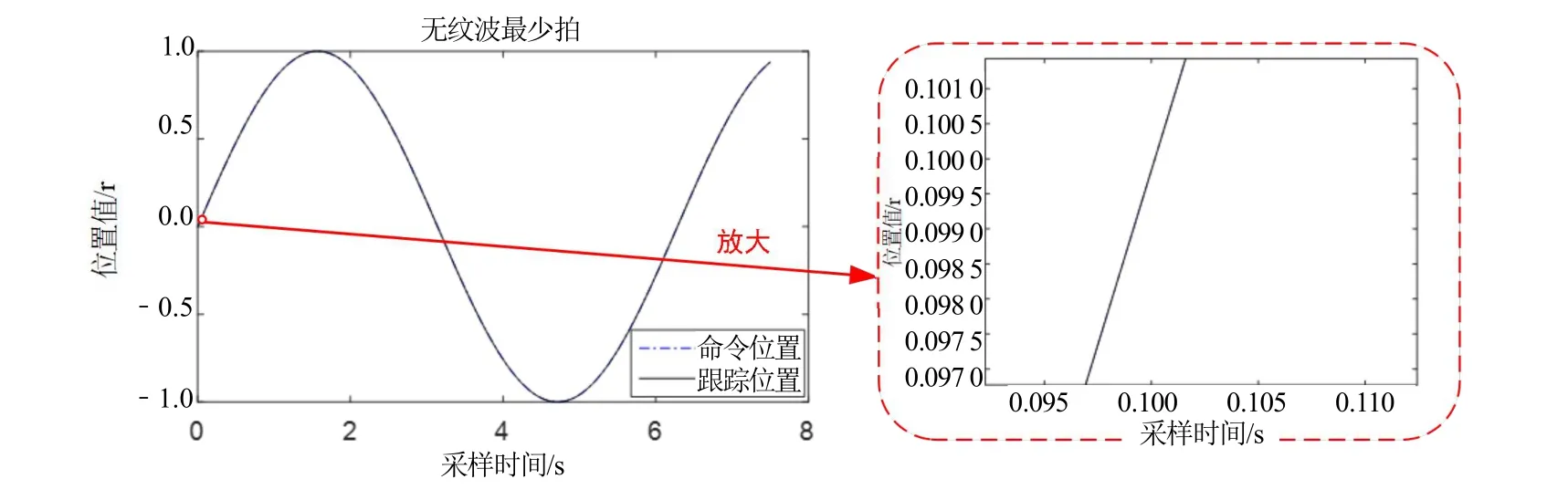
图6 单位频率正弦轨迹跟踪图

图7 3 种不同比例值对应的单位频率正弦轨迹跟踪图

3 结束语

针对激光跟踪仪测量跟踪时快速性和高精度的要求，笔者设计了一种能实现控制系统无纹波最少拍状态的位置环控制器，改进了常规的PMSM 三闭环控制系统，使PMSM 控制系统能以最少采样周期跟踪上运动轨迹，而且能避免纹波干扰造成系统损耗。通过仿真实验，验证了该系统相较常规的PMSM 三闭环控制系统具有明显的跟踪优越性。