基于贝叶斯网络模型的高速公路建设风险机制演化分析

张国华,王金成

(1.宁夏润通公路工程试验检测有限公司,宁夏 银川 750000;2.中国科学院长春光学精密机械与物理研究所,吉林 长春 130033;3.中国科学院大学,北京 100039)

1 引 言

高速公路建设是各地区实现互联互通的重要途径,也是国家整体经济发展的快车道。截至2021年底,我国交通运输部全年在高速公路建设上总投入高达2.6万亿元,同比增长6.0%[1]。在扩大规模的同时,各种人为因素、施工因素和环境因素所带来的风险也是建设中必不可少的考虑事项,高速公路建设中对风险机制的提前预警、过程分析和数据评估已经成为相关技术人员的研究重点。

为了构建更深层次的“多源一体化”动态数据评价系统,国内外专家学者针对风险因素的推理模型问题,衍生出诸多研究方法。按照对风险态势衍生级别的定性与定量分析来看,主要的研究方法有层次分析法[2],神经网络遗传算法[3],故障树分析法(FTA)[4],Meta分析法[5],Apriori算法[6]和贝叶斯网络模型[7]等。故障树统计模型和贝叶斯网络模型分别从定性和定量的角度来衡量事故重要度,将高速公路建设过程的风险等级进行逐级排序,但是目前的道路风险研究机制均是基于单源正向来构建次级风险的贝叶斯网络,而且考虑因素不完全,对于山区高速的“路-桥-隧”一体化风险机制有所欠缺。以西部地区的黎霍高速为例,基于故障树转化贝叶斯网络模型来求解高速公路建设中一些先验事件的风险概率。

2 故障树分析模型

2.1 基于故障树的风险识别分析

为了建立完整的风险评价体系,构建德尔菲法风险识别机制可以将致因因素考虑得更全面[8]。根据德尔菲法将这种复杂系统的风险因素划定为人为、道路、设备、环境和管理五大类。但是根据专家的细致讨论,一致认为管理因素是包含在其他四类之中的,在构建故障树时,中间事件就不单独考虑管理层面。在原有的德尔菲风险识别方法基础上将专家调查研究过程进行了改进,结合线上操作平台将风险识别过程简化,并且能在协同条件下更快更高效地完成全部工作。

1962年美国贝尔实验室根据逻辑命题和布尔代数运算首次提出FTA分析方法,该方法可以在任何简单或复杂系统内耦合其风险概率和安全性。FTA由顶上事件(T)、中间事件(M)、基本事件(X)等事件和与门、或门、非门、顺序与门、异或门等逻辑门构成。但是高速公路风险机制大多用“与”门和“或”门来搭建。通过改进型德尔菲法的讨论,构建了如图1所示的故障树模型,其中T1,T2,T3,T4代表次级顶事件。

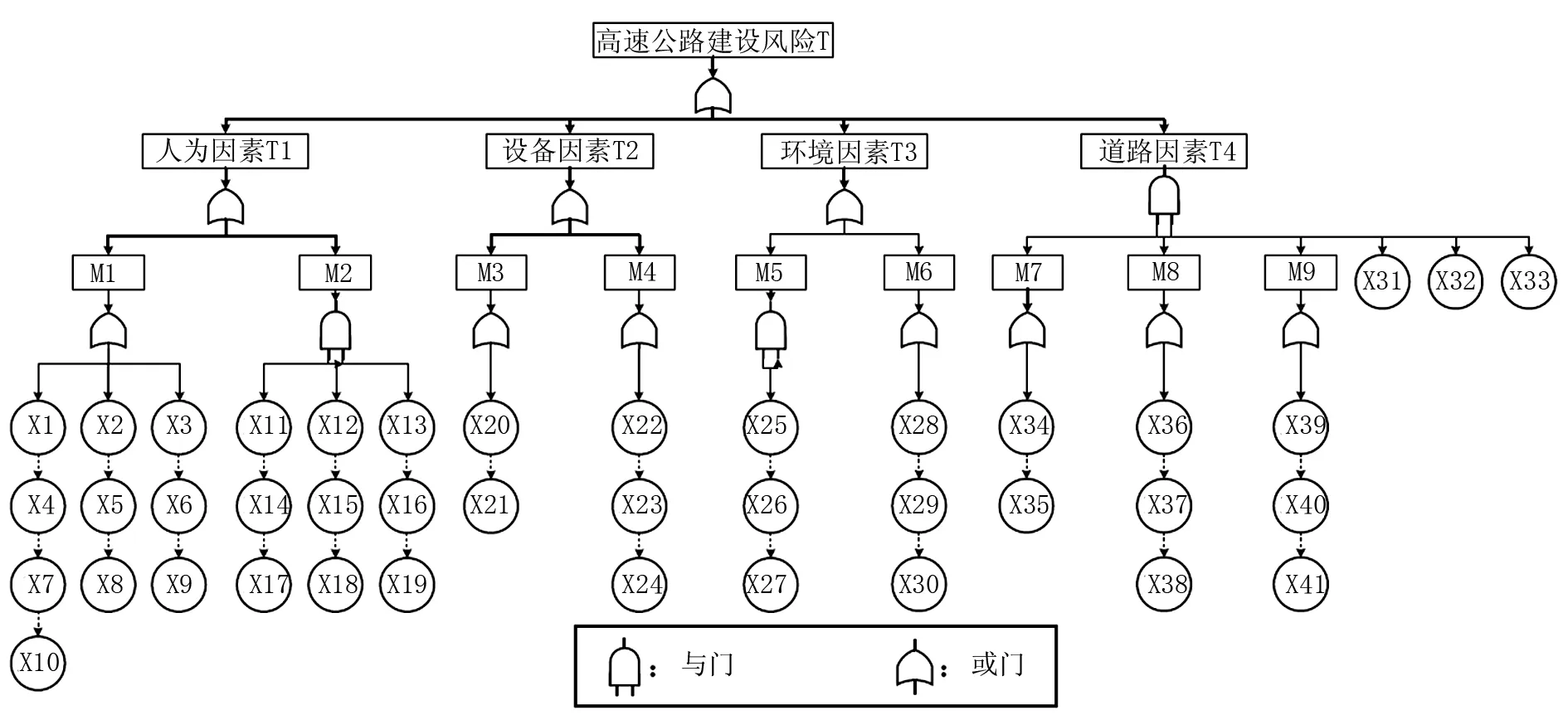
M1—人为主观因素;M2—人为客观因素;M3—设备自身因素;M4—设备相关因素;M5—交通环境因素;M6—自然环境因素;M7—道路因素;M8—隧道因素;M9—桥梁因素;X1—环境污染的防范;X2—地方政府的保护政策;X3—员工对薪金待遇不满;X4—部分工程技术难度大员工水平较差;X5—施工现场控制能力差;X6—业主拖延支付工程款;X7—业主资金短缺;X8—监理的协调不到位;X9—监理偏袒业主;X10—施工技术困难及新工艺的应用;X11—地方百姓的干扰;X12—合同管理水平不高;X13—合同工期较短;X14—施工质量要求高;X15—材料的短缺或材料不能按时到货;X16—材料价格可能上涨;X17—施工人员年龄大;X18—驾驶人员驾龄短;X19—驾驶人员疲劳驾驶;X20—施工机械设备落后;X21—施工机械设备故障;X22—供电供水的不稳定;X23—设备安装调试延期;X24—燃油供给不足;X25—工程机械量大;X26—监控、疏导不到位;X27—施工事故隐患;X28—严寒及酷暑降低工作率;X29—阴雨或洪水导致工程暂停;X30—火灾发生的概率较大;X31—路面潮湿;X32—夜间无照明;X33—山路居多易发生滑坡;X34—运输路面塌陷度高;X35—路面较窄;X36—隧道内设施缺陷;X37—隧道潮湿易坍塌;X38—仪器较大不易展开施工;X39—桥梁支柱不稳;X40—桥面较滑;X41—桥梁与路基衔接不牢。

2.2 故障树的数据结构分析

安全工程领域中结构重要度和最小割集重要度算法是对某一基本事件或其组合(割集)致使顶上事件出现故障的重要度进行定性计算的。最小割集是对故障树进行代数转化的有效途径,可以通过演绎的方式对该故障树模型进行重要度分析。分析中往往需要逐级分解,针对建立的故障树模型其结构函数可用公式(1)表示

(1)

式中:q为基本事件状态组合序号,且q=2n;Zi为状态分量;φq(X)等于0或1,表示不发生或发生。通过故障树的结构函数式(1)和布尔代数运算可得公式(2)。

T=T1+T2+T3+T4=(M1+M2)+(M3+M4)(M5+M6)+M7·M8·M9·X31·X32·X33=[(X1+…+X10)+(X11·…·X19)]+(X20+X21)+(X22+X23+X24)+X25·X26·X27+(X28+X29+X30)+(X34+X35)·(X36+X37+X38)·(X39+X40+X41)·X31·X32·X33

(2)

从公式(2)可知导致施工风险的途径有52条,每条途径基本事件最少1种,最多6种,而且1种的途径占50.2%,很容易引起事故。为了更清晰地表达建设过程中基本事件与顶事件之间的变化关系,通过公式(3)来表示i个事件的变化程度对顶事件变化的影响程度为

(3)

式中:P(T)为顶事件发生的概率;P(i)为第i个基本事件发生的概率假设顶事件必然发生概率为1,通过公式(3)可得各基本事件的概率重要度如表1所示。

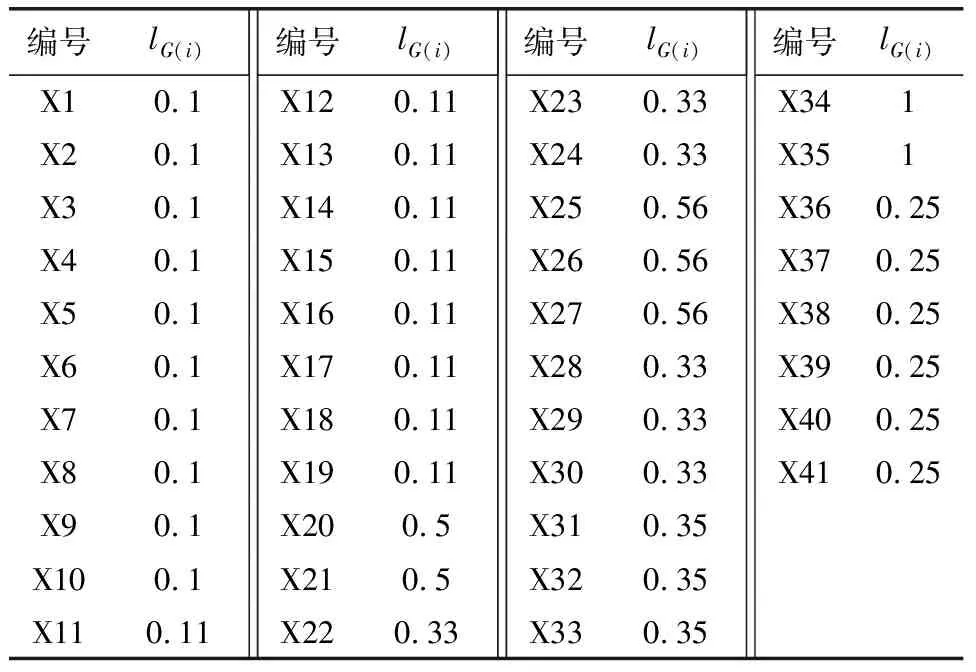
表1 基于故障树模型的基本事件概率重要度

假设可以通过计算重要度系数值来判定,通过构建公式(4)来表示最小割集重要度。

(4)

式中:N为最小割集总数;Eζ为第ζ个最小割集,Mζ为第ζ个最小割集的基本事件总数;i为事件序号。结合表中数据可知基本事件的重要度排序为lK(34)>lK(35)>lK(25)>lK(26)>lK(27)>lK(20)>lK(21)>lK(31)>=lK(32)=lK(33)>lK(28)>lK294)>lK(30)>lK(22)>lK(23)>lK(24)>lK(36)>…>lK(41)>lK(11)>>…>lK(19)>lK(1)>…>lK(10)。

结合公式(3)进行结构重要度分析可知路基情况是主要的风险因素,而且实际施工过程中主要应用的大型施工设备考虑的也是路面情况,人为因素和设备因素造成施工事故风险极低,周围环境因素在选址勘察时已经尽可能选取了最好的施工地址。

3 基于故障树构建贝叶斯网络模型

贝叶斯网络法相对其他风险评估分析模型而言不仅可以结合其中的某一种或多种方法进行综合评价,而且其节点可视化和简单操作是别的方法不可比拟的。贝叶斯网络模型的工作步骤与故障树的工作流程关联度极高,贝叶斯网络方法要先确定建设过程中的节点因素,然后分析其风险等级(顶事件、中间事件、底事件),紧接着要估计条件概率,给每个节点赋值,这是确定事件间关联度的必要条件,最终进行贝叶斯推理。贝叶斯概率表达式如公式(5)所示。

(5)

式中:P(F=f)称为节点的先验概率,表示不考虑事件B之前对事件F的概率进行估计,P(B=b|F=f)为条件概率,这里的先验概率由故障树基本事件概率确定,中间事件和顶事件的条件概率单独输入。前两个步骤正是故障树模型构建的过程,最终根据故障树和贝叶斯公式利用GeNIe分析软件构建的贝叶斯网络模型如图2所示。图中Y表示发生的概率,N表示不发生的概率,均为百分比。

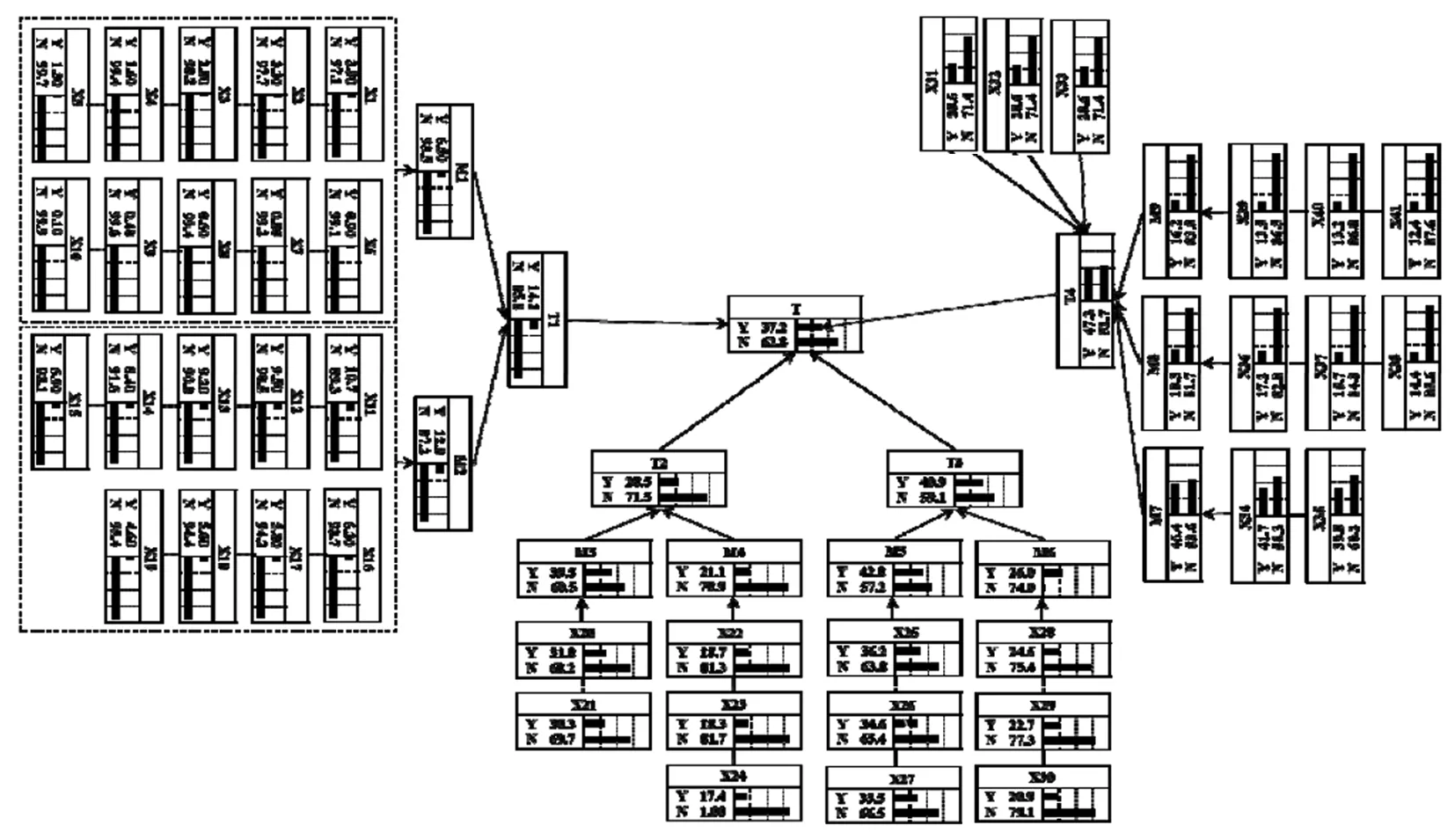
图2 基于故障树的黎霍高速公路一体化建设施工事故贝叶斯模型

由基本事件的重要度顺序和图2所示的贝叶斯概率模型可知在正向推理中故障树模型和贝叶斯网络的吻合度极高。这种方法将高密度高维度信息融合成多源具体化概率问题,以黎霍高速公路案例可知,施工路段的中间事件M4道路因素是最主要的事故致因源,其贝叶斯发生概率为47.3%,其包含的基本事件X34和X35发生概率分别为41.7%和39.8%;其次是周边交通环境因素,其贝叶斯发生概率为42.8,其包含的基本事件X25,X26和X27发生的概率分别为36.2%,34.6%和33.5%;设备自身因素的发生概率为39.5%,其包含的基本事件X20和X21的发生概率分别为31.8%和30.3%。其余基本事件和中间事件的概率均在30%以内,属于事故致因理论的安全范围。

在优化德尔菲法的协作下,该方法不仅可以将顶事件和各个层级的中间事件以及基本事件建立互联关系,还可以针对实际高速公路建设环境制定多模态安全策略。由于该案例中包含道路,桥梁,隧道,多模态安全策略主要是基于何种施工项目。在修设道路时由于道路因素占主要地位,可以针对该因素按照主次关系制定安全管理办法;同理在修设桥梁时考虑的主要是道路和设备因素;在修设隧道时主要考虑照明、滑坡、基础设施和环境因素。

4 结 论

依据在建的黎霍高速数据,将路-桥-隧一体化安全风险控制机制通过故障树模型和贝叶斯网络进行概率分析;故障树分析和贝叶斯网络概率模型的吻合度很高,对于人为、道路、环境、设备、管理等多源高密度安全信息进行融合;贝叶斯网计算简便,计算速度快,可同步更新信息,全局并行计算。根据黎霍高速风险机制,在此提出以下措施:(1)施工前加强基础设施的建设。(2)增加对施工设备的维护力度。(3)对施工人员进行定期培训考核。(4)保障供水供电。(5)对隧道内部环境进行实时检测。(6)提升桥梁施工的安全系数。(7)健全合同管理机制。通过多方的协调合作,健全安全风险管理机制将对高速公路一体化建设起到根本的保障作用。