软弱围岩偏压连拱隧道施工风险精准预测模型构建

余少华,严 江

(江西省交通设计研究院有限责任公司,江西 南昌 330000)

我国隧道工程的建设相对较为复杂,不仅是因为施工流程的繁琐,这在一定程度上也是因为复杂地质、地形所造成的[1]。软弱围岩由于强度低、稳定性差、变形持续时间长等,导致初支结构强烈变形甚至破坏,严重影响隧道施工和安全,对于隧道的建设,尤其是偏压连拱隧道的施工形成了一定的阻碍。为降低施工过程中的事故发生概率以及自然灾害的损坏范围,需要构建全覆盖式、系统的施工风险精准预测模型[2]。传统的施工风险预测模型一般是单向的,对于隧道工程内、外部结构存在的风险隐患可以进行快速处理,但是在实际应用的过程中,极容易受到工程变更或者外部因素的影响,导致预测结果不精准与不可靠[3]。因此,构建了软弱围岩偏压连拱隧道施工风险精准预测模型。考虑到最终预测结果的稳定性和安全性,需要选择较为真实的施工环境,根据实际的风险标准逐步构建更加灵活、多变的风险施工结构,有针对性地调整实际的风险预测流程,更为严谨地把控施工细节,以此来进一步增强实际的施工风险精准预测模型的应用能力,为后续的施工处理提供参考依据[4-5]。

1 构建偏压连拱隧道风险预测模型

1.1 提取风险预测因素

在完成对软弱围岩偏压连拱隧道施工风险精准预测模型的构建之前,需要先针对实际的工程施工需求及标准,提取对应的风险预测因素。通常情况下,风险预测一般具有较强的针对性,对于隧道施工的不同位置,所获取的数值信息也是不同的,需要有针对性地进行处理和提取。大致可以分为施工作业风险、材料运输风险以及现场作业风险三种。所提取的分类因素如表1所示。

表1 风险预测因素设定表

在完成对风险预测因素的设定之后,接下来根据实际的施工需求,对相应的施工预测区域做出划分。这部分可以从多个角度更改预测的方向,将单因素的提取与施工的各个环节相融合,为后续的风险预测模型的构建提供参考。

1.2 风险分级预测标准制定

在完成隧道施工的风险预测因素提取之后,需要结合实际的施工需求及标准,制定风险分级预测标准。常规的等级标准一般是依据工程的安全等级由低到高依次划定的,虽然可以完成预期的执行目标,但是针对于复杂的施工环境,极容易受到外部因素的影响,导致预测标准出现差异,出现预测等级混乱的问题。因此,需要根据施工隧道不同的状态及现状,构建对应的动态化风险分级预测标准。利用突变级数法,计算出归一风险均值,具体如公式(1)所示

G=β2+(γ1×0.5η)×γ1γ2

(1)

式中:G为归一风险均值;β为偏差系数;γ1为单向预测标准;γ2为预测误差;η为隧道覆盖区域,m2。

随后,将得出的归一风险均值作为分级预测的极限标准,再结合该隧道的风险综合评价等级,调整分级标准的变动区间,具体如表2所示。

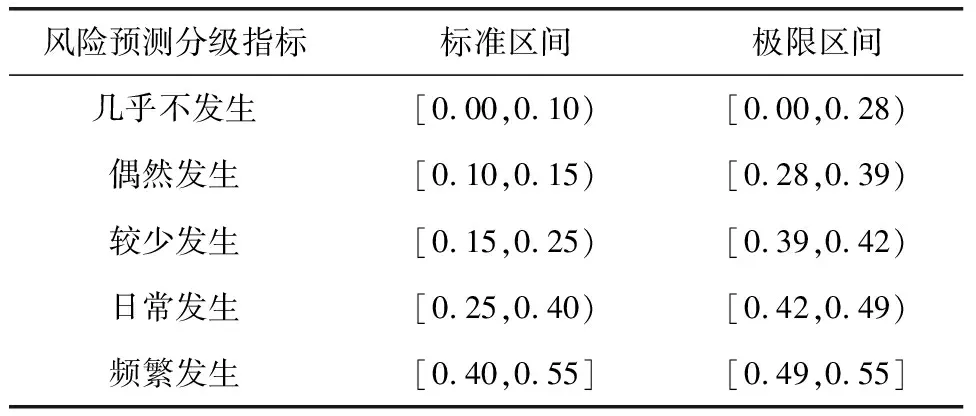
表2 分级标准变动区间设定表

最后,根据该隧道的建设需求及标准,调整分级标准,结合归一化处理模式和模糊综合评价法,测定出核心的分级预测标准点。

这部分需要注意的是,分级标准的设定一般是针对不同区域的,所以存在差异也是正常的,在进行风险预测结果汇总的过程中,结合统一的标准比照,以对应的比例缩小实际的预测差值,确保风险预测结果的精准、可靠即可。

1.3 隧道监测节点布设

在完成对风险分级预测标准的制定之后,接下来根据隧道的建设标准,根据软弱围岩偏压连拱隧道修建的延伸方向,设定软弱围岩偏压连拱隧道监测节点。这部分主要是利用监测控制节点,采集汇总实时的软弱围岩偏压连拱隧道施工数据,以此来为后续的预测工作奠定坚实的基础。利用模糊综合评价法在隧道中构建一个标定隧道监测空间,在隧道上方的承压截面上做出标记,并测算监测节点之间的距离,具体如公式(2)所示。

(2)

式中:U为监测节点之间的距离,m;v为标记点有效半径,m;Ψ1为预设覆盖范围,m2;Ψ2为监测半径,m;I为距离误差系数,无量纲。

通过上述计算,最终可以得出实际的监测节点之间距离。结合得出的结果,依据预测的范围,对监测节点之间的距离进行多方位调整,根据隧道施工量以及路段的变化,做出监测节点的标记与监测节点的关联,以此采集软弱围岩偏压连拱隧道相关数据,此处以隧道左线冲沟地段纵断面为例,具体如图1所示。

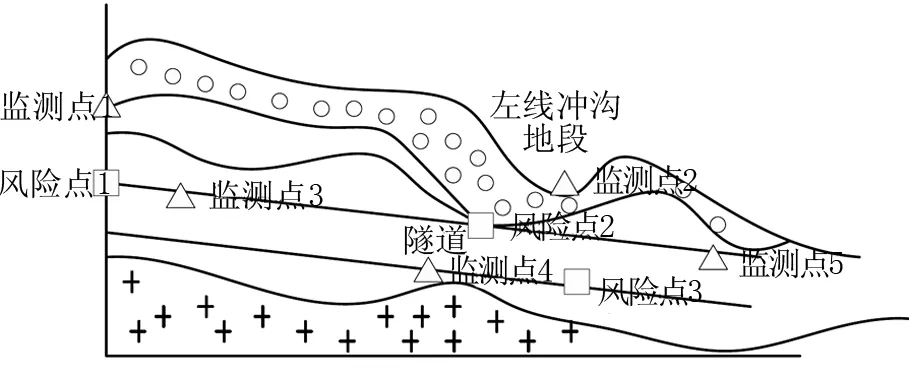
图1 隧道左线冲沟地段地质纵断面

根据图1,可以完成对隧道左线冲沟地段地质纵断面的分析和研究。根据隧道中此路段的风险现状,布设对应的监测节点,对其余的隧道路段做出标记,完成数据采集环境的搭建。

1.4 梯形风险预测矩阵构建

在完成对软弱围岩偏压连拱隧道监测节点的布设之后,接下来结合软弱围岩偏压连拱隧道的施工需求及标准,逐步构建梯形风险预测矩阵。这部分可以采用熵权及模糊综合评判法,测定出模型组建的基础数值及信息,提升软弱围岩偏压连拱隧道施工风险预测精准度与效率。

通常情况下,对于软弱围岩偏压连拱隧道的风险预测是较为复杂的,需要考虑到周围关联工程的情况,也要提前对隧道外部的承压能力调研,分析隧道坍塌的概率。完成基础工作的处理之后,接下来针对环境风险、勘察设计风险、施工风险以及材料控制风险等,设定对应的风险预测矩阵的层级。进行主观预测权重的计算,具体如公式(3)所示。

(3)

式中:D为主观预测权重;m为自然风险概率,%;n为定向评语集,个;π为风险归类差值。通过上述计算,最终可以得出实际的主观预测权重。结合得出的主观预测权重,可以分析出模型内部的预测偏重比例,并对预测整体结构做出有效调整。针对此时隧道修建情况的变化,对存在的隐藏风险做出描述,获取基础的预测评价指标数值,具体如表3所示。

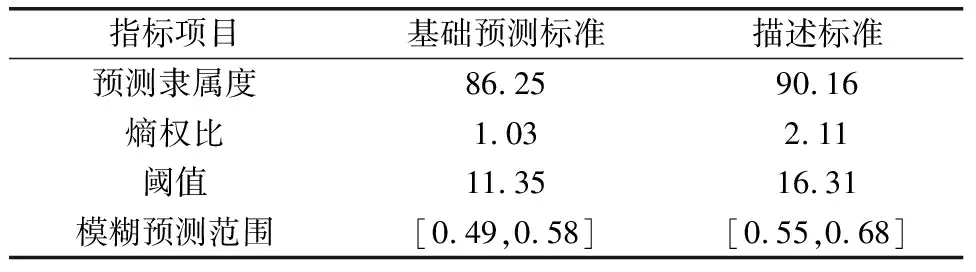
表3 基础预测评价指标数值设定表

根据表3,可以完成对基础预测评价指标数值的设定与比照调整。随后,需要结合工程进度的推进,更改模型整体的风险预测范围以及区域,实现动态化的风险预测处理。这部分需要注意的是,为增强实际的风险评价效果,降低总体的风险评价误差,可以在每一个调整风险预测范围时构建一个风险预测评语集,针对地势以及路段的变化,更改、调整矩阵中的预测指标项目。结合施工中存在风险的大小,逐步进行对应预测等级的进一步划分。根据预测节点所收集的实时数据,将预测目标依据梯形的框架排布,具体如图2所示。

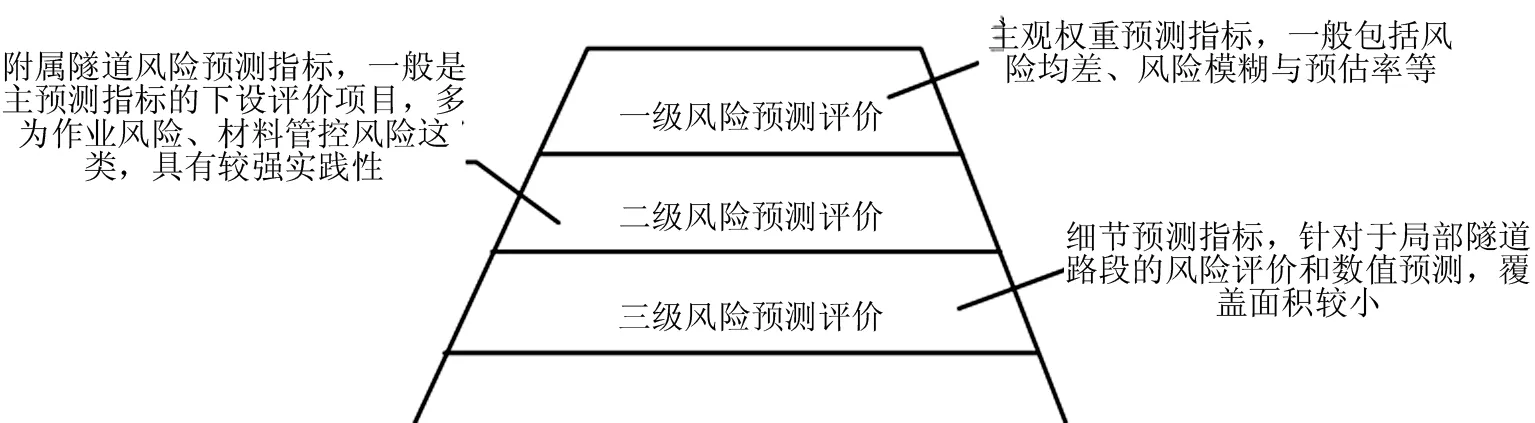
图2 梯形风险预测矩阵结构图示

根据图2,可以完成对梯形风险预测矩阵结构的设计。根据隧道施工路段的不同状态和需求,调整对应区域监测节点的布置和设定,为预测矩阵的应用构建一个动态化的环境,结合模糊综合评价法完成梯形风险预测矩阵的设计。

1.5 随机森林实现风险预测

在完成对梯形风险预测矩阵的构建之后,结合实际的需求和标准,接下来可以采用随机森林预测法实现隧道预测模型的构建。以江西省萍乡中环路安源隧道项目作为测试的对象,该隧道位于我国的东南部,地处国家级森林公园,地质为标准的软弱围岩区域。经过调查可以发现,隧道的修建位置地表还被古樟树群所围绕。隧道的中心位置地势较高,与煤矿采空区及巷道相互依托,平截面和纵断面两部分多处交叉增加了隧道的外部承压。

安源隧道位于萍乡市安源区安源镇安源煤矿附近,为一连拱式隧道,其起止桩号为K6+514～K6+660,隧道长度为146 m,净空为2×13.25 m×5 m,该隧道属于公路短隧道。隧址区属于低山丘陵区,地质条件复杂,施工安全风险高,施工难度大。该隧道整体处于边坡偏压浅埋区域,内部结构较为紧密,设定的隧道预埋深度为35 m,侧方承压结构的深度为15 m,内部构建为三车道的连拱隧道,隧道整体的内置跨度已可以达到31 m,是我国建设程度十分复杂的偏压连拱隧道。

随着隧道的修建进度,调整实际监测节点的位置,利用随机森林算法模式实现动态化预测。软弱围岩偏压连拱隧道分为几个部分,关联相同区域内的节点,在实际的软弱围岩偏压连拱隧道施工风险预测过程中,随机挑选一个监测节点,采集其中的相关数据,结合Bootstrap重抽样法进行随机测定和决策性的数据集构建,在标定的范围之内,获取模型的数据集单元,在不同的路段环境下,测定出实际的预测不平衡系数,具体如表4所示。

表4 不同路段预测不平衡系数表

根据表4,可以完成对不同路段预测不平衡系数的分析与获取。随后,结合随机路段不平衡系数的变化,测定出预测结果的准确度,细化预测模型的实际执行能力,最终实现软弱围岩偏压连拱隧道施工风险精准预测模型的构建。

2 结果分析

随机选取4个基本路段,测定风险预测模型的真实误报率,具体如公式(4)所示。

L=μs2×(o1-so2)

(4)

式中:L为风险预测模型的真实误报率,%;μ为模型灵敏度,是单位时间内输出的风险预测结果;s为预测均值;o1为特异值;o2为随机差值。

通过上述计算,最终可以得出实际的风险预测模型真实误报率,对获取的结果比照分析,具体如表5所示。

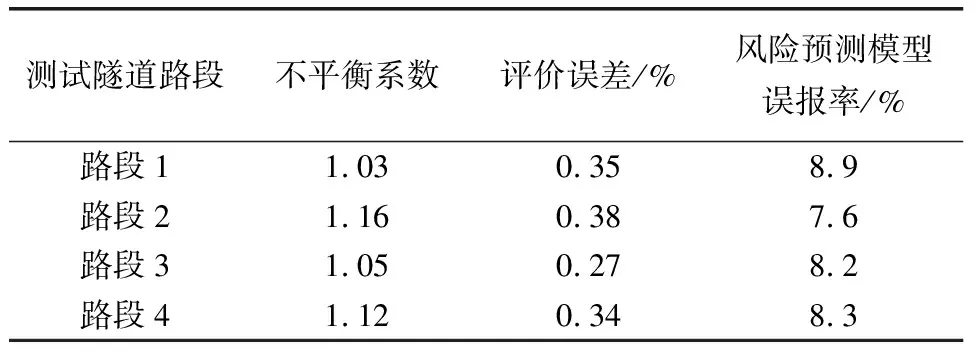
表5 测试结果对比分析表

根据表5可知,经过4个路段的测定分析,最终得出的软弱围岩偏压连拱隧道施工风险预测模型误报率均控制在10%以下,表明在实际应用的过程中,该模型的风险预测能力较强,误差小,更为可控,具有较高的实际应用价值。

为了进一步验证所设计模型的优越性,将传统模型作为实验对比方法,比较了不同模型的预测精准度,结果如表6所示。

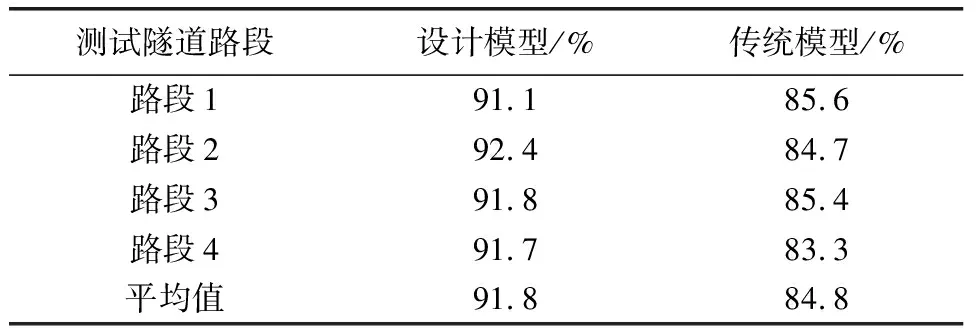
表6 不同模型预测精准度比较结果

分析表6中的数据可知,所设计模型的软弱围岩偏压连拱隧道施工风险预测模型预测精准度最大值为92.4%,平均值为91.8%,最小值为91.1%;传统的软弱围岩偏压连拱隧道施工风险预测模型预测精准度最大值为85.6%,平均值为84.8%,最小值为83.3%;综合分析上述实验结果可知,所设计模型的预测精准度远远高于传统模型,说明利用该模型可以得出精准的软弱围岩偏压连拱隧道施工风险预测结果。

在上述实验的基础上,比较了所设计模型与传统模型的软弱围岩偏压连拱隧道施工风险预测耗时,结果如表7所示。

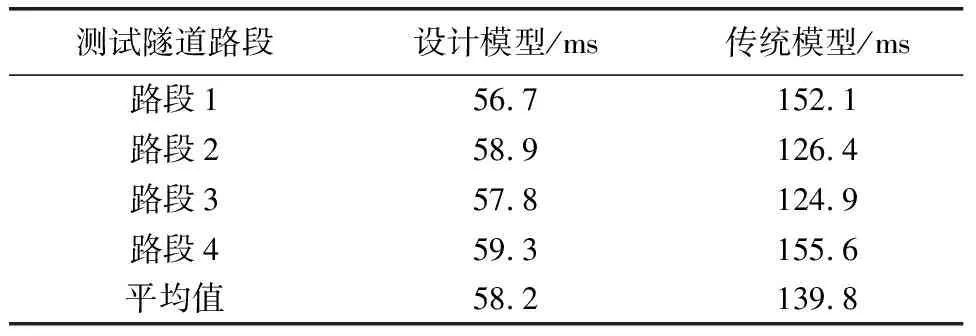
表7 不同模型预测耗时比较结果

分析表7中的结果可知,所设计模型与传统模型对于不同测试路段的软弱围岩偏压连拱隧道施工风险预测耗时存在一定的差异性,其中设计模型的软弱围岩偏压连拱隧道施工风险预测耗时最大值为59.3 ms,平均值为58.2 ms,最小值为56.7 ms;传统模型的软弱围岩偏压连拱隧道施工风险预测耗时最大值为155.6 ms,平均值为139.8 ms,最小值为124.9 ms;与设计模型相比,传统模型的预测耗时很长,说明这种模型的执行效率不高,而利用所设计模型可以快速获取软弱围岩偏压连拱隧道施工风险预测结果,整体预测效率较高,实际应用效果较好。

3 结束语

综上所述,完成了对软弱围岩偏压连拱隧道施工风险精准预测模型构建的分析与验证,主要结合真实的施工场景,通过调整对应的预测指标体系,归纳与提取总结隐藏的风险因素,完成对风险的归类。与此同时,针对此基础,进行预测结构的调整和重置,从多个方面进一步克服传统预测模型存在的偏倚问题,保证软弱围岩偏压连拱隧道施工风险预测结果变得更加真实可靠,为隧道施工营造一个更为安全、稳定的环境,保证软弱围岩偏压连拱隧道施工的安全顺利进行。