轻型客车垂向振动与俯仰振动的耦合性分析

邓跃跃，谢能烽

（1.特百佳动力科技股份有限公司，上海 201506；2.深圳技术大学城市交通与物流学院，广东 深圳 518118）

1 引言

垂向振动与俯仰振动是评价汽车平顺性的主要指标，但是汽车是一个复杂的系统，车身垂直振动与俯仰振动之间存在耦合现象，与之相关的研究也越来越多，文献[1] 在研究该问题时假定前后悬架的振动是非耦合的，这与实际情况差异较大；文献[2] 从功率的角度深入分析了垂向振动与俯仰振动的耦合关系，但是仿真计算时没有考虑整车系统非线性问题。

本文采用刚柔耦合动力学仿真方法和整车道路试验方法，揭示某车型的振动耦合关系。并对影响车身振动耦合性的悬挂质量分配系数进行系统性分析，为悬架系统参数的匹配设计提供参考，具有实际的工程应用价值。

2 垂向振动与俯仰振动耦合机理

图1为车身振动多体动力学简化模型，整车质量m等效地分解为前轴上、后轴上和质心上3 个集中质量mf、mr和mc。整车质心处的俯仰角β 与前后桥簧载质量的垂向位移zf和zr幅值及zf和zr的相位差有关，当相位差为180°时，俯仰角最大，同时俯仰角与轴距L 成反比关系；当相位差为0 时，质心处垂向位移zc最大。

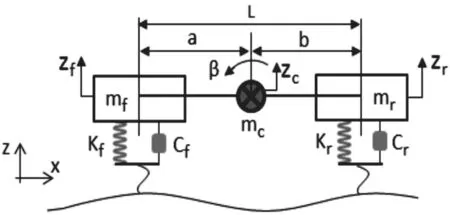
图1 车身振动模型

文献[4] 推导出的3 个集中质量表达式为：

式中，py为车身绕横轴y 的回转半径，a 为整车质心到前轴距离，b 为整车质心到后轴距离，L 为轴距。当悬挂质量分配系数ε=1 时，并且刚度中心与质量中心重合时，质心处垂向振动与俯仰振动不存在耦合现象，相应振型如图2（a）所示；但是汽车悬挂质量分配系数多数为0.8 ～1.2，mc多数不为零，质心处垂向振动与俯仰振动存在耦合现象，相应振型如图2（b）所示。通过上述分析可知，悬挂质量分配系数是影响车身垂向振动与俯仰振动耦合现象的主要因素。

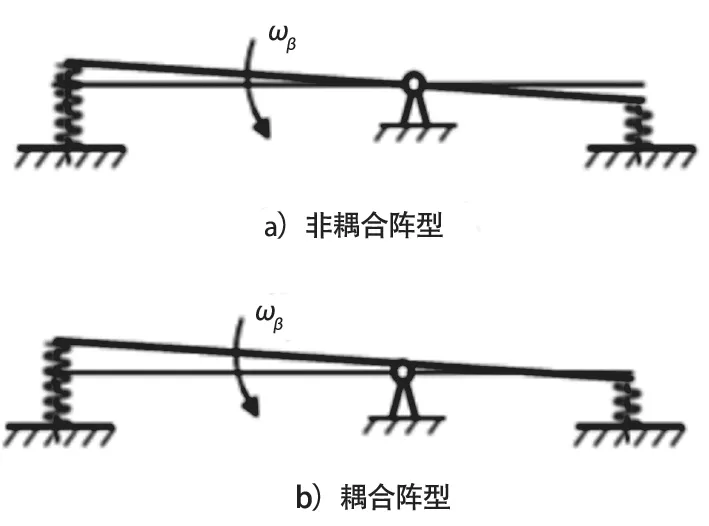
图2 车身振动振型简图

3 悬挂质量分配系数确定

3.1 悬挂质量分配系数计算方法

先假设悬挂质量分配系数为1，利用公式（2）计算a 和b 的值，式中mf′和mr′为前后悬架簧载质量实际测试值。

采用修正系数法计算车身绕横轴y 的转动惯量Jy，K1和K 为经验修正系数；对于单后轴车辆K1=0.48，对于双后轴车辆K1=0.5；K 的取值为0.3～0.4，对于大型车辆取上限，小型车辆取下限。

再利用公式（4）（5）便可以计算出悬 挂质量分配系数ε。

3.2 工程应用

以某车型为例，利用上述方法计算悬挂质量的分配系数。整车承载量不同时，质量分配系数一般不同，文中分别计算空载和满载条件下的整车质量分配系数。两种工况下，前悬架簧载质量实际测试值为1323kg、1530kg，后悬架簧载质量实际测试值为1790kg、2520kg，轴距为3310mm，取K1=0.48，K=0.35，计算结果如表1 所示。

表1 质量参数计算表

4 振动耦合仿真与试验

4.1 多体建模

目前，国内大多数的设计公司、科研院所和汽车公司多采用ADAMS/CAR 中的四立柱虚拟试验台对整车平顺性能进行仿真。由于四立柱虚拟试验台只能输入Z 向位移激励模拟道路垂直冲击振动，忽略了其他两向激励的影响；轮胎模型多采用系统自带的PAC2002 魔术轮胎或Ftire 轮胎模型，不能够真实地反应轮胎的性能，因此，仿真精度较低。本文根据三轴六自由度整车试验台的工作原理，创建三轴三自由度虚拟试验台，实现X 方向、Y 方向和Z 方向上的激励输入，同时避免轮胎模型不确定性对系统的影响，激励输入位置为四个轴头处，分析悬架参数对平顺性影响，将创建好的整车刚柔耦合多体模型搭载在虚拟试验台上，如图3 所示。

图3 整车多体模型

图中的弹簧作用是控制模型在X 方向、Y 方向上和Z 方向上的位移量，防止模型产生大的刚体位移。

4.2 仿真与试验分析

在前后悬架上方车架模型上创建加速度测量点，并依次给前后轴一个Z 向阶跃信号，观察车架上测量点位置处的振动加速度曲线，通过对比车架前后端加速度曲线来定性分析振动能量传递过程，并对前后悬架振动相关性进行分析。并按照《GB 4783-84 汽车悬挂系统的固有频率和阻尼比测定方法》对整车振动特性进行测试，加速度测试位置要与多体模型中的测试位置一一对应，如图4 所示。

图4 加速度传感器布置

取空载工况时的仿真数据与试验数据进行对比，验证建模方法和仿真结果的准确性，为质心位置优化做准备，对比结果如图5 和图6 所示。

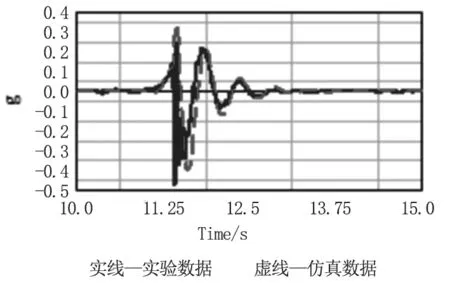
图5 前悬架对比结果

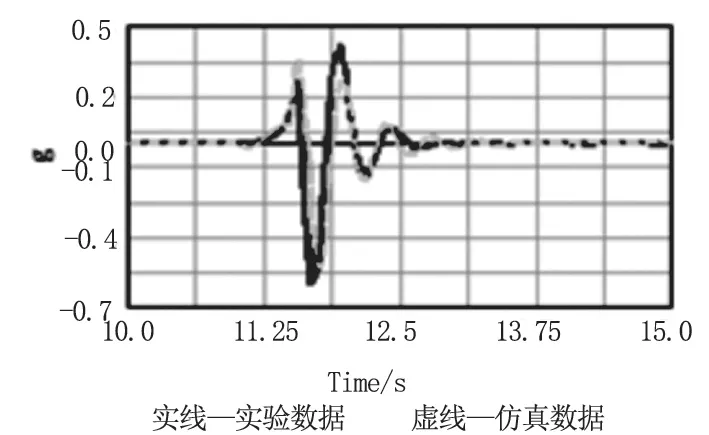
图6 后悬架对比结果

从图5 和图6 可知，空载工况的试验结果与仿真结果吻合度较高，验证了建模方法和仿真结果的准确性，可以利用此模型进行优化分析。空载工况，前后悬架振动试验结果如图7 ～8 所示。

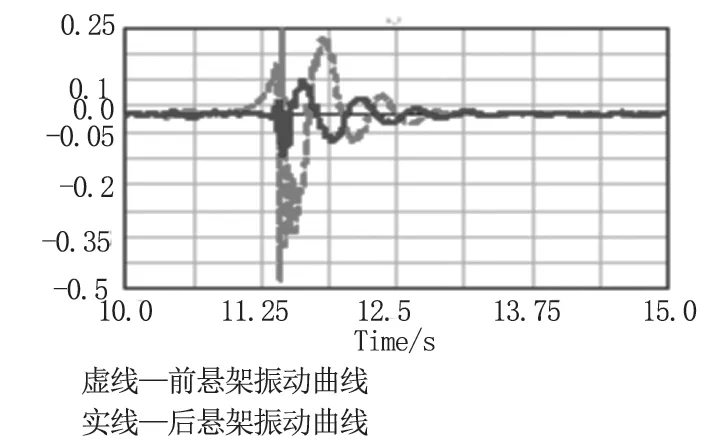
图7 空载工况前轮激励测试结果

图7 是前轮激励时的加速度测试数据，前悬架加速度幅值为0.22g，后悬架加速度幅值为0.0413g，两者幅值比为5.33。图8 是后轮激励时的加速度测试数据，后悬架加速度幅值为0.42g，前悬架加速度幅值为0.0762g，两者幅值比为5.51。从幅值比可以看出，空载工况时前后悬架振动相互影响的程度近似相同。

满载工况，前后悬架振动试验结果如图9 ～10 所示。图9 是前轮激励时的加速度测试数据，前悬架加速度幅值为0.202g，后悬架加速度幅值为0.057g，两者幅值比为3.54。图10 是后轮激励时的加速度测试数据，后悬架加速度幅值为0.338g，前悬架加速度幅值为0.0446g，两者幅值比为7.57。从幅值比可以看出，满载工况前悬架振动对后悬架的影响要远大于后悬架对前悬架的影响。

前后悬架幅值比在一定程度上反映了振动能量传递的大小，即悬架间的振动相关性。影响前后悬架振动相关性的因素主要有整车质量分配系数、前后悬架刚度与阻尼比、前后悬架的连接方式，本文从整车质量分配系数角度出发对整车系统进行优化，降低悬架间振动的相关性。

5 参数优化

由表1 可知，空载时整车质量分配系数约等于1，悬架间振动相关性主要由车架连接方式引起；满载时整车质量分配系数为1.17，是造成悬架间振动关联度较高的主要原因，需要对质量分配系数进行优化。文中利用建立好的整车多体模型，对整车质心坐标进行参数化优化，使车辆在满载工况下前后悬架振动相关度最小，即加速度振幅比最小。满载工况时，质心在X 方向上的初始坐标为1944.6mm。经过参数化优化后质心在X 方向上的坐标为1867.3mm，并对优化结果进行仿真验证。当前轮激励时, 前/ 后悬架加速度幅值为比为4.66，当后轮激励时,后/前悬架加速度幅值为比为6.13，与原方案相比，优化结果有了较好的改善。

6 结语

（1）对车身垂直振动与俯仰振动的耦合机理做了详细的分析，并详细介绍了质量分配系数的求解方法。

（2）不同载重量，某车辆的垂向振动与俯仰振动相关性不同，空载工况时2 种振动的解耦性最好。

（3）仿真结果与试验数据吻合性较高，说明模型精度较高，仿真方法可靠。

（4）整车质量分配系数是影响垂向振动与俯仰振动耦合性的重要因素，当其值为1 时，并保证刚度中心与质量中心重合时，2 种振动解耦性最佳。