基于线性方程-Adam算法的微震震源定位研究*

赵扬锋,赵 伟,王进铭,潘一山,3

(1.辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000;2.辽宁省矿山沉陷灾害防治重点实验室,辽宁 阜新 123000;3.辽宁大学 灾害岩体力学研究所,辽宁 沈阳 110036)

0 引言

随着我国国民经济的高速发展,矿山资源开发由浅层逐渐转向深部开采,矿山灾害日益频发,矿山微震震源定位反演作为微震监测系统的核心技术,对矿山灾害的预警有重要意义。

微震事件定位方法中,有基于射线追踪原理的定位方法、线性定位法及非线性定位法。射线追踪技术用于微震震源定位主要是Julian等[1]提出2点间射线追踪方法。Nakanishi等[2]将图形网络理论引入到射线路径计算中,提出最短路径射线追踪法。在此基础,上王辉等[3]提出将单纯形法与最短射线路径追踪法相结合的微震震源定位法,利用最短射线路径追踪法计算检波器到潜在震源点的反向射线路径,再在单纯形法计算得到的初始解区间内求节点走时-到时差之和最小值,该最小值对应的节点即为震源点。Peng等[4]提出基于Log-Cosh的震源定位的目标函数,为提高定位准确度和稳定性剔除掉较远距离的传感器P波到时数据,提高定位准确度及稳定性。线性定位法是针对微震参数数据未知量建立线性方程组的数学求解方法,在线性定位法中应用较广的是Geiger法,Geiger法是Geiger[5]将定位非线性问题转化为线性问题求解,利用震源位置坐标和发震时刻建立线性方程组,对方程组使用一阶泰勒展开后用最小二乘法求解参数方程得到震源位置。Waldhause等[6]提出双差定位法(HYPODD),采用绝对走时和互相关P波和S波差分走时,当所有观测到的事件与监测站台联系在一起时,观测到时和理论传播时差之间的双差最小,通过迭代调整互相关震源之间的向量差,得到最小二乘解。线性定位法计算效率高,但可能会陷入局部最优解,因此有学者提出非线性定位法。

非线性定位法可以避免陷入局部最优解,其主要是建立震源位置的目标函数,使用不同的算法求解目标函数最小值,得出震源位置坐标。典型的非线性定位法有网格搜索法[7]、牛顿法[8]、梯度下降法[9]等。其中,网格搜索法引入较复杂的速度模型,定位精度较高,但网格划分的疏密程度对计算速度和效率有很大的影响。梯度下降法是一阶优化算法,初始值的选取对定位精度有极大影响。牛顿法是二阶最优化算法,迭代次数少,若初始点选取合理,算法很快收敛。

除了提高算法本身的定位准确度之外,有学者将算法与其他算法相结合进行联合定位,提高算法定位的准确度及稳定性。林峰等[10]提出线性定位和Geiger定位相结合的联合定位法。用线性定位进行初步定位,再以线性定位解作为Geiger定位法的迭代初值进行求解。姜天琪等[11]提出1种将网格搜索法与牛顿法相结合的震源定位算法,利用网格搜索法为牛顿法提供迭代初值进行震源定位,能够有效避免由于迭代初值选取不当造成定位失败,提高了牛顿法定位准确度和稳定性。此外,微震监测台网的布置对定位精度有较大影响,因此刘晓明等[12]提出矿山微震监测台网的综合评价指标,为监测台网的布置提供一定的理论支持。

多数震源定位方法需要预先给定速度模型,速度模型精度直接影响定位结果准确性。针对速度模型对定位精度造成的不利影响,本文采用Adam算法[13]对震源进行反演定位,通过设置不同的P波波速来验证波速对定位结果的影响,结果显示该算法能够有效避免测速误差对定位精度造成不利影响。此外,为提升算法定位的稳定性,将线性方程法求得的初次定位解作为Adam算法的初始迭代值。

1 线性方程-Adam算法原理以及实现步骤

对矿山微震事件进行定位,利用微震波走时进行定位反演。在井下合理布置监测台站形成监测结构,通过各个监测台站检波器以及被激发微震信号的P波到时,建立走时方程如式(1)所示:

(1)

式中:ti是矿震微震信号P波到时时刻,s;t0是发震时刻,s;(xi,yi,zi)是第i个站台坐标,m;(x0,y0,z0)是震源坐标,m;V是P波波速,m/s。

根据式(1)建立目标函数,如式(2)所示:

(2)

式中:n为站台传感器数量。

1.1 线性方程定位法的定位原理

线性方程定位法忽略了复杂的速度模型,用对确定区域震源进行简化的方法,从未知的震中(x0,y0,z0)到站台检波器(xi,yi,zi)(i=1,…,n)之间距离的斜直线来计算微震走时T,如式(3)所示:

(3)

式中:T为微震信号P波计算走时,s。

将式(3)进行变换,如式(4)所示:

(4)

其中震源参数(x0,y0,z0,t0)是以下n-1个线性方程组的最小二乘解,如式(5)所示:

A·θ=r

(5)

式中:θ为震源参数向量(x0,y0,z0,t0)T;A是震源参数的系数矩阵;r是作差后的向量。

A和r如式(6)～(7)所示:

(6)

(7)

该方法至少需要5个站台的P波到时,无需反复迭代,在本文中用于Adam算法的初始迭代值。

1.2 Adam算法原理

Adam算法由梯度下降算法改进得到,相比于标准的梯度下降算法,Adam算法引入指数加权移动平均值对梯度值进行估计同时又增加了偏置修正,修正从初始化原点一阶矩和非中心的二阶矩估计,使迭代更快速收敛,同时避免陷入局部极小值。

假设有目标函数f(x1,x2,x3,…,xn),其中(x1,x2,x3,…,xn)是待更新参数,Adam算法的目的是求解该目标函数最小值;f1(x),f2(x)…fT(x)表示在后续的时间步1,2…T上的迭代更新。用gt=∇xft(x)表示目标函数f(x)的梯度。标准梯度下降算法按照式(8)来更新参数:

xt=xt-1-αgt

(8)

式中:xt为待更新参数向量;α为步长因子。

Adam算法引入指数加权移动平均值,如式(9)所示:

vt=βvt-1+(1-β)gt

(9)

式中:vt为指数移动平均值,初始化值为0;β∈[0,1]是控制指数衰减率的超参数。

当β取值接近0时,历史信息对当前梯度影响较小,这导致优化曲线中包含更多的噪声,会导致算法震荡或者不稳定的更新;当β取值接近1时,历史信息对当前梯度影响较大,算法优化更加稳定,但收敛速度较慢,适用于包含噪声较大的数据集。

在式(9)中计算指数加权移动平均值时需初始化v0=0,这导致第一项为零,使v1的估计值偏于零。因此在计算指数加权移动平均值时,为使得结果更加准确,引入偏差修正,如式(10)所示:

(10)

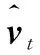
Adam算法的更新规则如下:

1)初始化一阶矩、二阶矩变量s=0,u=0,以及矩估计的指数衰减率,β1,β2∈[0,1]。

2)根据式(9)计算梯度的有偏一阶矩估计和梯度的二阶矩估计,如式(11)～(12)所示:

st=β1st-1+(1-β1)gt

(11)

式中:st为梯度的一阶矩估计。

(12)

式中:ut为梯度的二阶矩估计。

考虑到矿山开采环境的复杂性,β1和β2的选取按照Kingma[13]设置的默认值进行计算,即β1=0.9,β2=0.99。

3)根据式(10)修正一阶和二阶矩偏差,如式(13)～(14)所示:

(13)

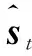
(14)

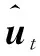
4)基于梯度下降更新参数,如式(15)所示:

(15)

式中:δ是用于数值稳定的小常数,取10-8。

1.3 线性方程-Adam算法用于震源定位步骤

由式(2)给定初值(x1,y1,z1,t1)进行迭代使目标函数达到最小值,得到震源空间位置。根据式(2)将目标函数做如下变化,如式(16)所示:

(16)

线性方程-Adam算法用于微震事件定位时的具体实现步骤如下:

1)首先读取各个检波器的位置数据及相应的P波到时数据。

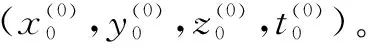
3)设定Adam算法的步长因子α,再将步骤2)计算得到的初步定位解作为Adam算法的初始迭代值进行求解计算。

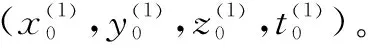
5)在每次的迭代循环内设置迭代终止条件,即迭代到某次时目标函数的值不再下降时跳出循环,输出迭代后的震源位置坐标。

6)重复步骤4)～5),直至达到迭代终止条件。

线性方程-Adam迭代法的流程图如图1所示。

2 线性方程-Adam算法模拟实验及结果

2.1 线性方程-Adam算法模拟实验方案

线性方程-Adam算法模拟实验如图2所示,设置的监测区域范围是2 000 m×2 000 m×1 500 m,图2中正方体表示检波器,球体表示微震事件,1～4是位于监测区域内的震源,5～6是监测区域外部的震源,各点的坐标如表1～2所示。

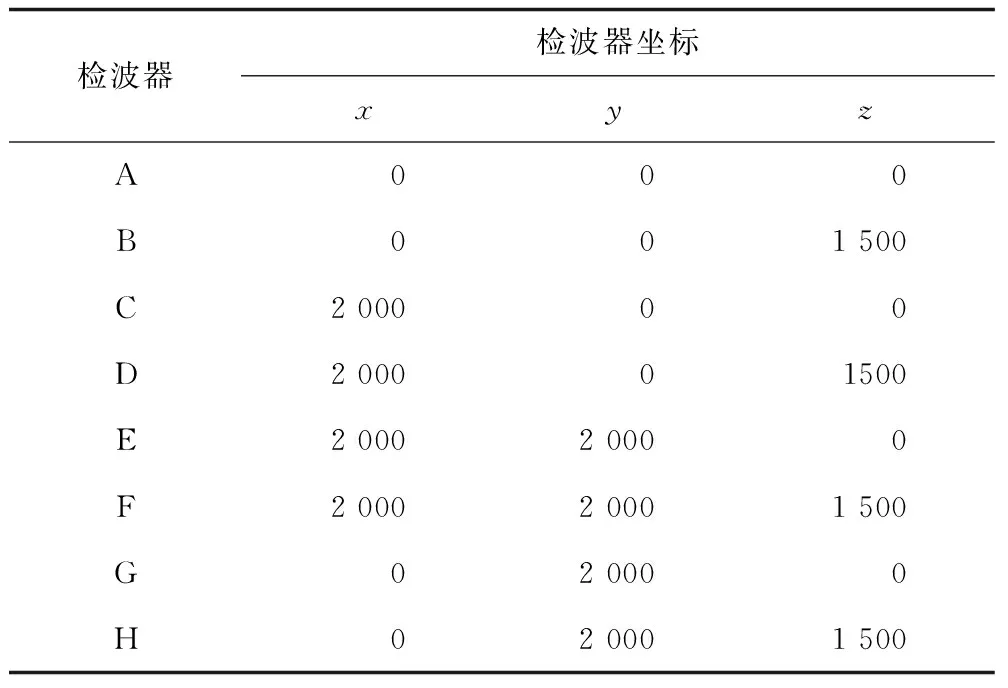
表1 仿真模型各检波器坐标Table 1 The coordinates of each detector in the simulation model 单位:m

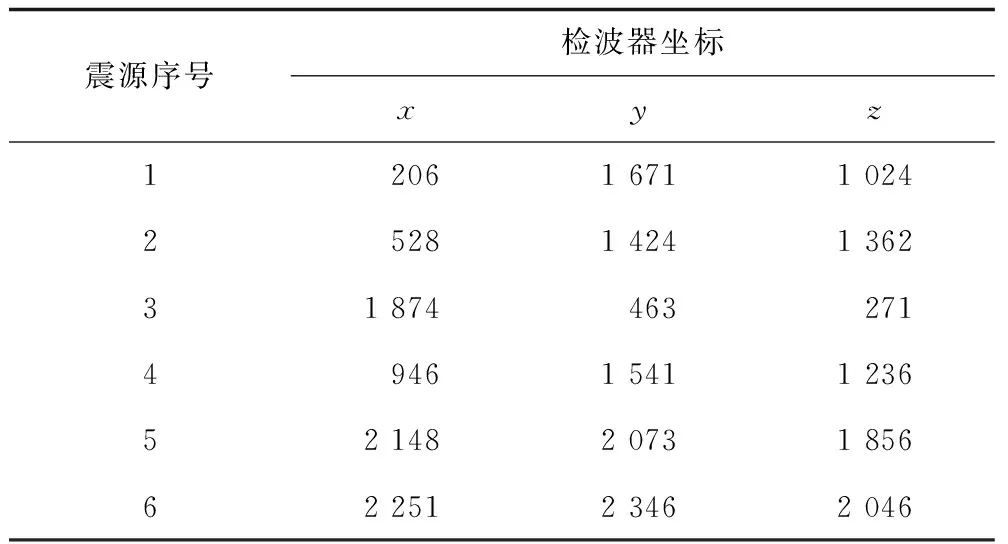
表2 仿真模型各震源坐标Table 2 The source coordinates of the simulation model 单位:m

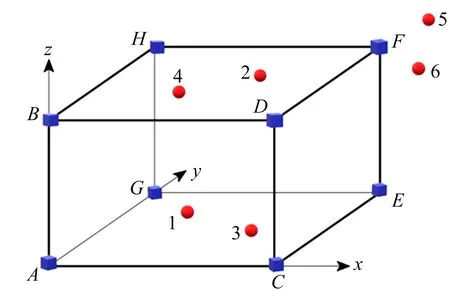
图2 检波器与微震事件分布Fig.2 Detector and microseismic event distribution

设现在微震P波平均波速为4 500 m/s,发震时刻0 s,按各个震源到检波器的距离计算得到P波到时,如表3所示。

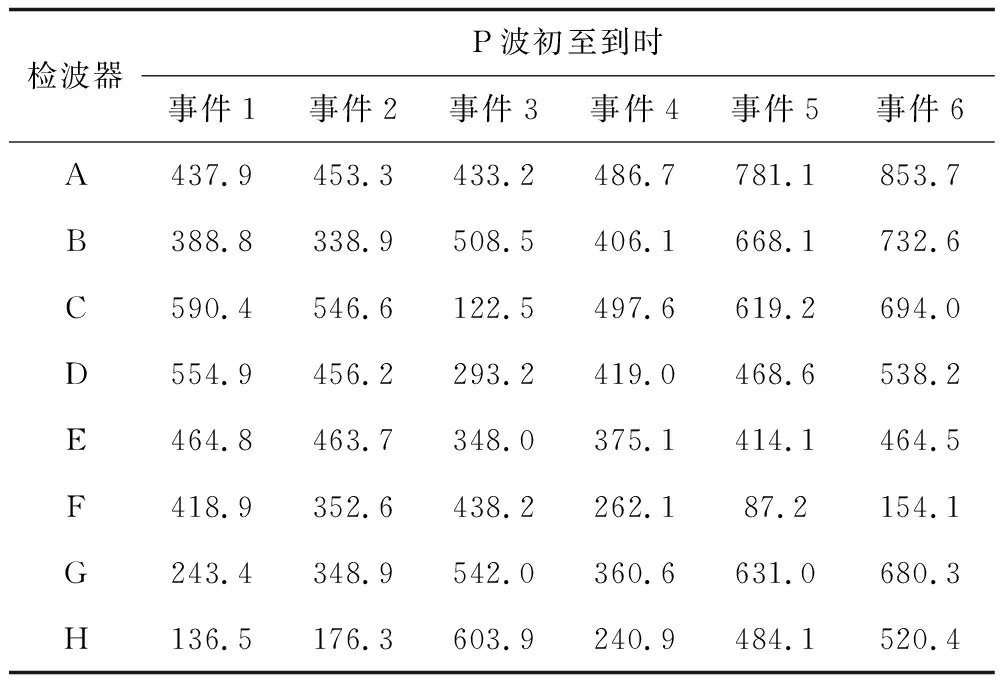
表3 仿真模型P波初至到时Table 3 Simulation model P wave first arrival time 单位:ms

在实际工程中,地下煤岩的各向异性使P波在传播过程中的波速是不断发生变化的,测得的波速会存在误差,在一些优化算法中,如网格搜索法、模拟退火法等,速度参数对定位结果有显著影响。因此本文将介质的各向异性体现在速度参数上,具体做法参考李健等[14]关于速度各向异性模型处理,在平均速度的基础上随机分配3%和5%的速度波动范围,表4为在速度各向异性条件下的P波初至时间。

表4 速度各向异性下的P波初至时间Table 4 P wave first arrival time under velocity anisotropy 单位:ms

2.2 定位结果分析

2.2.1 步长因子对定位结果影响

Adam算法在对目标函数优化时,初始迭代值选定后,利用空间距离公式计算得到定位坐标与震源坐标之间的总误差,如式(17)所示,不同步长因子定位结果见表5。步长因子对定位结果的影响由算法本身的性质和目标函数决定,与震源位置无关,因此表5选择微震事件1计算得到的定位误差,其他微震事件同样适用于此规律。

表5 步长因子对定位结果的影响Table 5 The influence of step factor on the positioning results 单位:m

(17)

式中:d为定位总误差,m;(x,y,z)为定位坐标,m;(x0,y0,z0)为震源坐标,m。

由表5可知,随着步长因子从0.1逐渐减小到0.001时,定位误差在减少。但当步长因子从0.001减小到0.000 1时,定位误差在增加。这是由于单步迭代算法在迭代计算时,计算机字长有限,每一步运算均需四舍五入,因此迭代的每一步会产生舍入误差。从收敛性结果来看,步长因子越小即步长越小,结果越准确;但从舍入误差来看,计算步数的增多导致舍入误差积累,最终使得计算结果失真,因此,选择步长因子10-3进行迭代。

2.2.2 迭代初值对定位结果的影响

对于大多数优化算法而言,迭代初值的选取会直接影响算法能否寻找到全局最优解,进而影响到定位结果。同样,Adam迭代算法的结果也会受到迭代初值的影响。在速度参数确定后,不同的迭代初值对定位结果的影响如表6所示,表6中每个微震事件的第1个迭代初值为线性方程法的定位解,其余2个迭代初值为随机初始值。

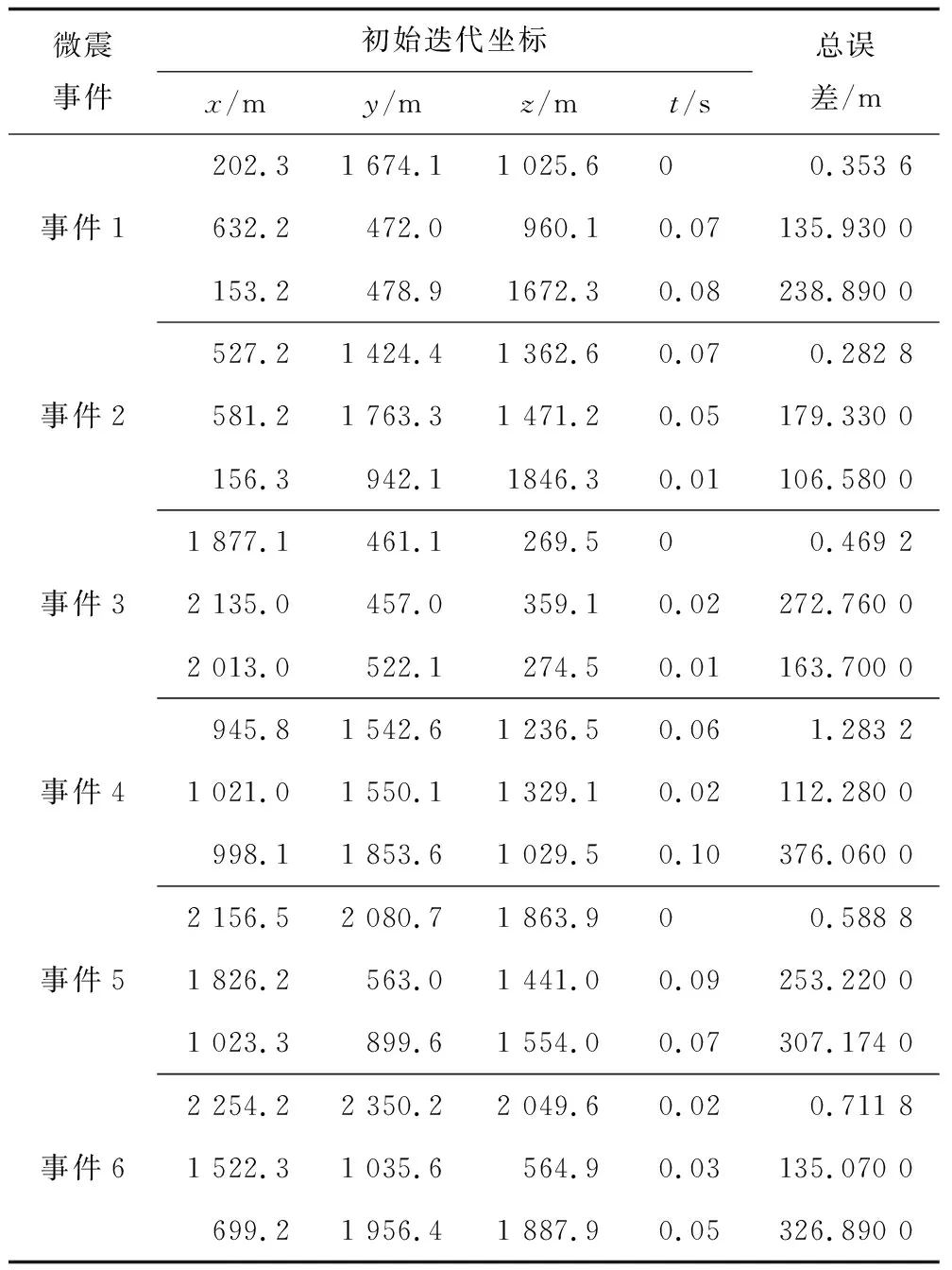
表6 不同迭代初值对定位结果的影响Table 6 The influence of different iterative initial values on the positioning results

观察表6中每个微震事件不同的迭代初值的总误差,选择线性定位法的定位结果作为Adam算法的初始迭代值时,每个事件的总误差均小于1 m,由随机初始化得到的迭代初值的定位总误差均在100 m以上,甚至达到300 m。因此每个微震事件的定位结果,迭代初值的不同对定位结果影响较大,而选取线性定位法的结果作为迭代初值,其定位准确度较高。

2.2.3 速度参数对定位结果的影响

为验证和比较线性方程-Adam定位法的准确性以及稳定性,本文分别选取线性方程-Adam算法、牛顿迭代法、模拟退火法、Geiger定位法4种方法对表3～4数据进行反演定位。此外,为更贴合实际的工作环境,加入测速误差对总定位结果的影响。

在速度各向异性的干扰下,测速误差分别为0,-3%,3%,即速度分别是4 500,4 365,4 635 m/s,4种方法的定位误差如图3所示。图3中编号见表7。

表7 图例编号Table 7 Legend number

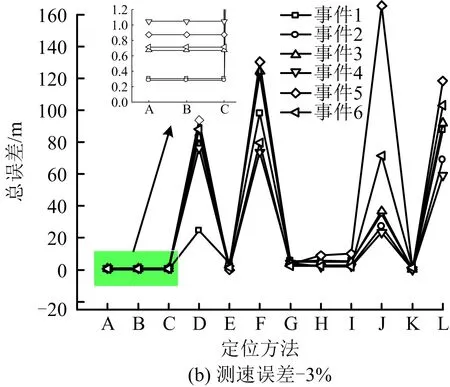
图3 速度各向异性和测速误差影响下的定位误差对比Fig.3 Comparison of positioning errors under influence of velocity anisotropy and velocity measurement error

1)速度各向异性对定位结果的影响。图3(a)中的定位准确度折线展示了在无测速误差情况下,速度各向异性对定位结果的影响。图3中的6条折线代表6个微震事件在速度各向异性条件下,使用不同定位方法得到的定位结果。图3中的横坐标表示各种方法对应的速度各向异性范围,以微震事件1为例,利用牛顿迭代法定位,D、E、F分别表示牛顿迭代法在速度各向异性为0、3%和5%时,微震事件1的定位总误差。

各向异性范围为0时,图中的附图结果显示,线性方程-Adam法、牛顿迭代法、模拟退火法以及Geiger法的定位结果相对准确。

当各向异性范围为3%时,图3(a)中的附图结果显示,线性方程-Adam法的定位结果没有受到影响,而其他方法均受到不同程度的影响。观察横坐标E代表的牛顿迭代法,在各向异性范围为3%时,定位总误差明显增加。模拟退火法在各向异性范围为3%时,对微震事件的定位误差虽有增加,但误差在可接受范围内。而Geiger法在速度各向异性范围的影响下,对微震事件的定位误差最大。

各向异性范围为5%时,线性方程-Adam算法对各微震事件仍然能准确定位,而其余3种方法对各微震事件定位结果误差均较大。综合上述定位方法与线性方程-Adam算法的对比,在速度各向异性的条件下,只有线性方程-Adam法能够实现准确定位。

2)测速误差对定位结果的影响。速度各向异性范围为0的条件下,对比分析测速误差对定位结果的影响。观察对比图3(a)～图3(c)中横坐标A、D、G、J对应的定位总误差,对比图3(a)～图3(c)的附图横坐标A,线性方程-Adam算法对各微震事件定位的结果显示,在各向异性范围为0时,不同的测速误差对定位结果不会产生影响。对比图3(a)～图3(c)的横坐标D,结果显示随测速误差的增加,牛顿迭代法对各微震事件定位的误差在增大。对比图3(a)～图3(c)的横坐标G,结果显示随测速误差的增加,模拟退火法对各微震事件定位的误差相差较小,因此测速误差对模拟退火的定位影响较小,但模拟退火法的定位准确度和稳定性要稍劣于线性方程-Adam算法。对比图3(a)～图3(c)的横坐标J,结果显示随着测速误差的增加,Geiger法对各微震事件的定位误差在增大,测速误差对Geiger法的影响比对牛顿迭代法的影响还要大。线性方程-Adam算法不会受测速误差的影响,测速误差对模拟退火的影响较小,对牛顿迭代法和Geiger法的影响较大。

3)速度各向异性和测速误差的综合影响。图3(a)～图3(c)中横坐标B,C,E,F,H,I,K,L表示当速度各向异性范围达到3%和5%时,各定位方法在测速误差分别为-3%和3%时的定位误差,可以观察到线性方程-Adam算法的定位仍然没有发生变化,而牛顿迭代法的定位误差有显著的增大,其定位结果不理想,定位稳定性变差,模拟退火法的定位误差没有太大的变化,Geiger法的定位误差有明显的增大。

综合上述分析,Adam算法由线性方程确定迭代初值后,对微震事件的定位结果不受速度各向异性和测速误差的影响。这是由目标函数和算法参数更新策略决定,为使式(2)的目标函数达到最小值,可以认为将P波波速和P波走时作为1个整体参数,而震源位置参数作为另外1个整体参数。Adam算法在搜索目标函数最小值更新参数时看作更新2个整体参数即震源位置参数和由P波波速及P波走时组成的整体参数,若调整P波波速,为保证目标函数的最小值,算法更新P波走时抵消P波波速的变化导致目标函数最小值的变化,最终表现为P波波速不会影响定位精确度。但这会导致P波走时误差增大,而检波器收集到的P波到时是固定的,因此最后的误差就会累积到发震时刻。本质上是以发震时刻的准确度为代价。本文研究的是震后反演定位,因此对过去的发震时刻没有太高的要求。

3 工程实例验证

本文利用林峰等[10]在柿竹园矿区爆破实验以及刘超等[15]人工爆破实验。在柿竹园矿区内测得的爆破坐标为(8 732.70,6 570.60,511.30),此次爆破实验共计8个传感器接收到微震信号,实验测得的P波波速为5 000 m/s,8个台站位置信息以及P波到时如表8所示。

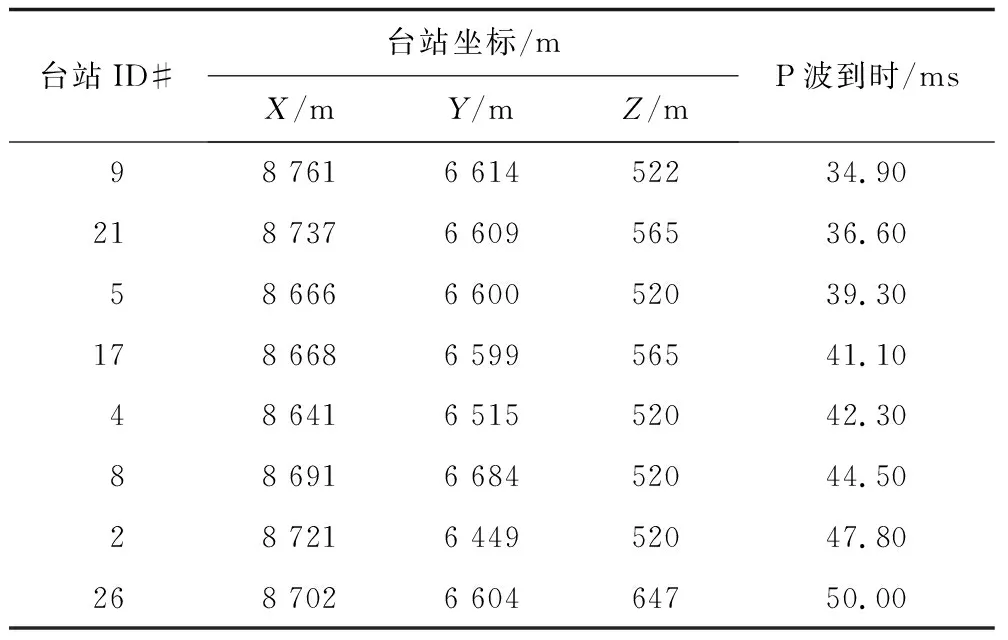
表8 柿竹园台站坐标及P波初至到时Table 8 The coordinates of Shizhuyuan station and the first arrival time of P wave

刘超等[15]进行的人工爆破实验使用5个检波器收集爆破信号,在监测区域煤岩体内最优化的P波传播速度为2 572.5 m/s,测得的爆破坐标(4 290,7 255,-676),台站坐标和P波到时如表9所示。

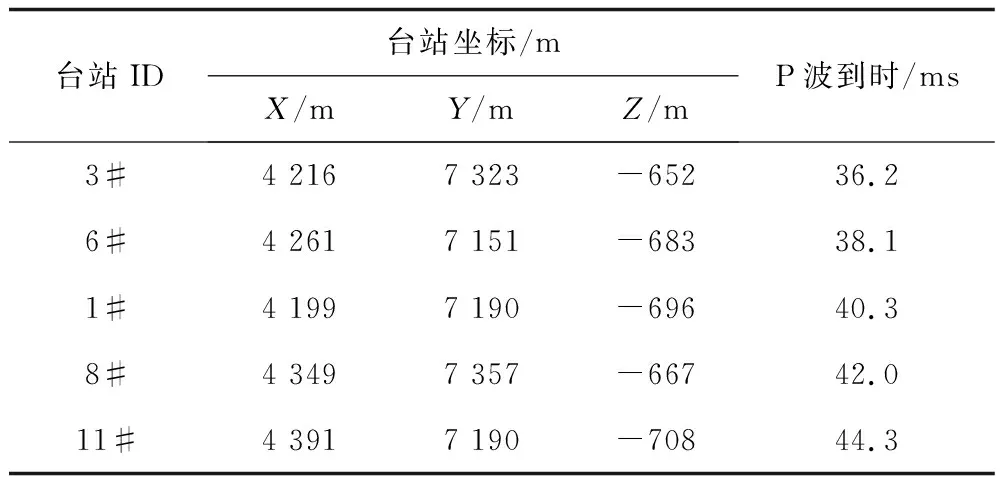
表9 人工爆破台站坐标及P波初至到时Table 9 The coordinates of artificial blasting station and the first arrival time of P wave

将相应的定位参数带入线性方程-Adam算法进行定位,与模拟退火-单纯形法、Geiger法、牛顿迭代法定位结果进行比较见表10和表11。2类爆破实验的定位结果显示,线性方程-Adam定位法相比于其他定位方法,定位准确度有一定的提高。模拟退火法每次定位都能靠近真实震源空间位置,但因其采用空间随机搜索模式,每次定位结果都不同,导致定位结果不稳定;Geiger法的定位结果受速度参数影响较大;牛顿法定位需要求二阶导数的Hessian矩阵增加了计算量;线性方程-Adam算法在迭代过程中,确定迭代初值后定位结果不受速度参数的影响,且在相同的初始条件下,每次的定位结果都是相同的。

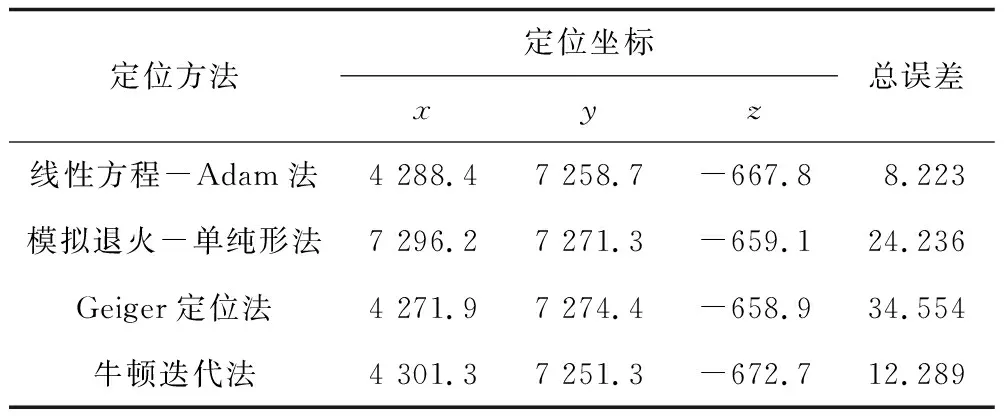
表11 人工爆破实验定位结果对比分析Table 11 Comparative analysis of positioning results in artificial blasting test 单位:m

4 结论

1)线性方程-Adam震源定位法,利用线性方程的初次定位解作为Adam算法的迭代初值提升了Adam算法定位的稳定性,并有效避免迭代初值选择不当对定位准确度的影响。

2)利用柿竹园矿爆破数据对算法进行验证,结果显示线性方程-Adam定位法相比于牛顿迭代法无需计算二阶导数,节省计算资源,且定位精度提高了54%;相比于模拟退火法-单纯形法定位精度提高了67%;相比于Geiger法定位精度提高了82%。

3)利用刘超等人工爆破实验对算法验证,结果显示线性方程-Adam定位法相比于牛顿迭代法定位精度提升了33%,相比于模拟退火-单纯形法定位精度提升了66%,相比于Geiger法定位精度提升了74%。

4)线性方程-Adam定位法相比于其他算法,无需预先获取复杂的速度模型,迭代初值确定后,其定位结果不会受测速误差影响。