勾股定理的中国发现

叶智超 整理

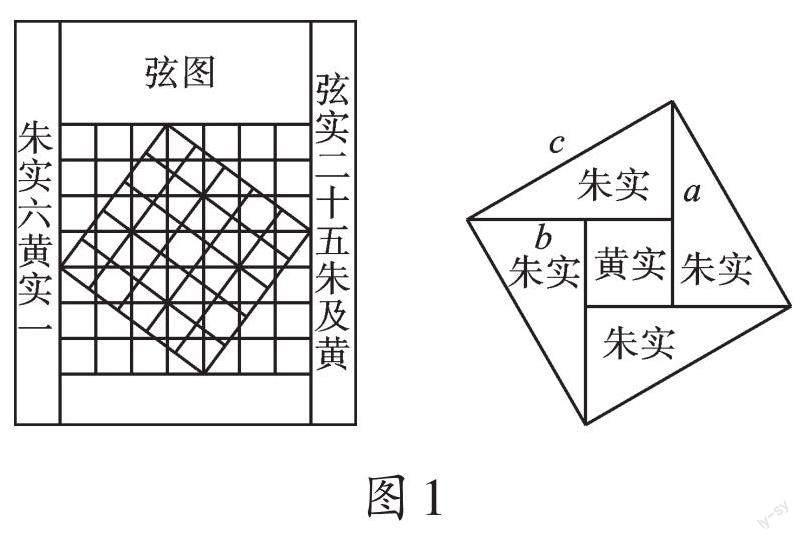
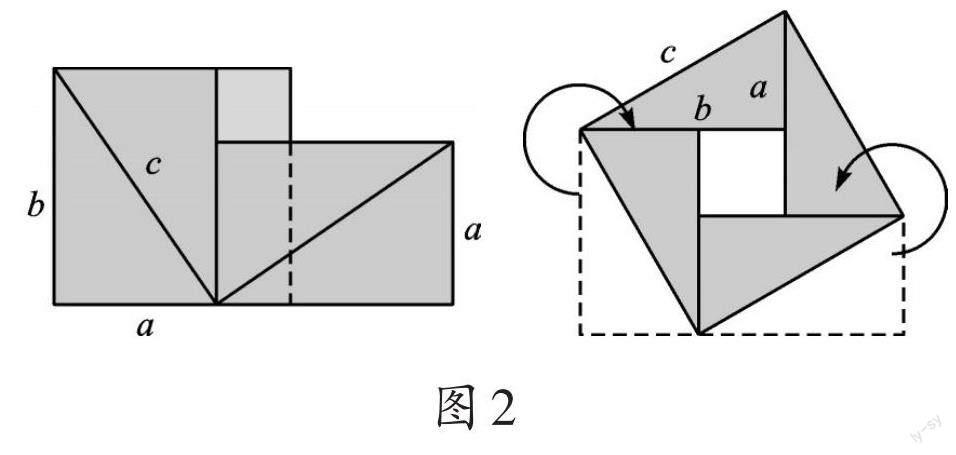
三国时期的赵爽创作了《勾股圆方图说》。他画了一张“弦图”（如图1）表述勾股定理，其证明思路：每一个直角三角形称为“朱实”，中间的一个正方形称为“中黄实”，以弦为边的大正方形叫作“弦实”。赵爽将“勾三股四弦五”一般化才形成了真正的勾股定理，其證明过程有图为证（如图2），永载史册。赵爽证明勾股定理的这个方法可谓精妙绝伦，成为将代数和几何紧密结合，使之互不可分的一个典范。这个无字证明（不用数学语言证明）的方法被哈佛大学教授库里奇称为“最省力的证明”。因此，“赵爽弦图”被选为2002年国际数学家大会会徽，现在这个标志也成了中国数学会的标志。

刘徽通过“青朱出入图”（如图3）也证明了勾股定理。同时，他把“赵爽弦图”和“青朱出入图”所蕴含的思想方法总结为“出入相补”原理。“青朱出入图”巧妙地利用了“出入相补”原理，且蕴含动态思想，具有科学创新的意义。

勾股定理启发了人类对数学的深入思考，促成了三角学、解析几何学的建立，为数学的进一步发展拓宽了道路。因此，勾股定理和黄金分割被誉为“几何双宝”，前者好似珠玉，后者堪称黄金。

（作者单位：南京航空航天大学附属初级中学）