论计算匀质半球体质心的微元选取
曾 山
(中国矿业大学化工学院 江苏 徐州 221116)
质心是一个很重要的概念,其实质心是与质心系质量分布有关的一个代表点,它的位置在平均意义上代表着质量分布的中心.我们要研究物体的整体运动,就只需找到这个物体的质心,则物体任何一部分的运动一般都可以分解为质心的运动和物体该部分相对于质心的运动.
1 质心的定义
如图1所示的物体,我们用mi和ri表示物体系统中第i个质点的质量和位矢,则质心C的3个直角坐标被定义为
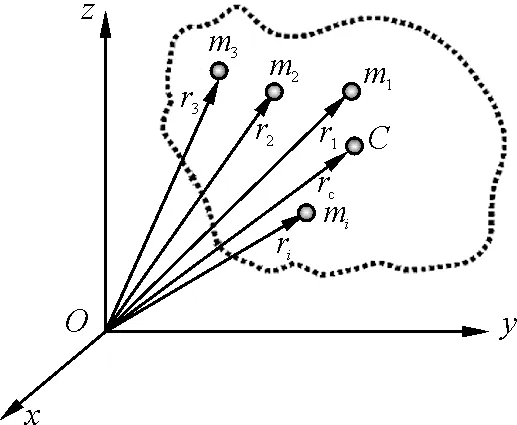
图1 质心的位置
其矢量式为
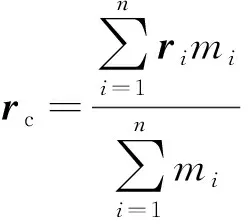
对质量连续的物体,如本文将讨论的匀质半球体,可以当成质点系,质点就成为微小的质量元,把求和改为积分,即
2 问题的引入
计算一半径为R、质量为M的匀质半球体的质心位置,通过5种微元的选取方法来得到结果.不妨设其密度为ρ.
3 微元的选取
3.1 直角坐标系下取dxdydz
如图2所示,半球体可看作无穷多个长方体,其边长分别为dx、dy和dz.我们选用最常用的体积微元dV=dxdydz,则质量微元
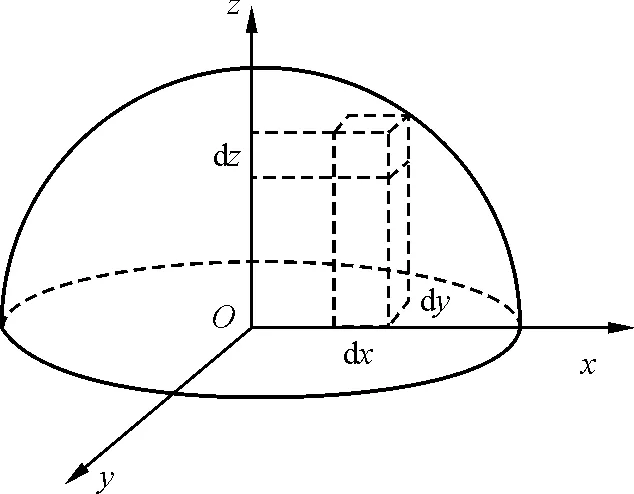
图2 半球体可看作无穷多个长方体
dm=ρdV=ρdxdydz
对其积分
而半球体质量M可表示为
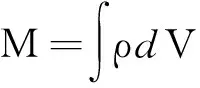
即
(1)
从而得到
3.2 柱坐标系下取dθdrdz
如图3所示,半球体可看作无穷多个柱体,其底面积为rdθdr,高为dz.从而选取体积微元dV=rdθdrdz,则质量微元
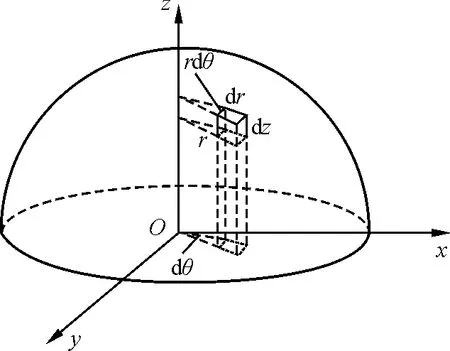
图3 半球体可看作无穷多个柱体
dm=ρrdθdrdz
对其积分
与式(1)联立,从而得到
3.3 球坐标系下取dθdφdr
如图4所示,在球面坐标系下,半球体可看作无穷多个曲面六面体的组合,这些曲面六面体可近似看作长方体,其经线方向的长为rdφ,纬线方向的宽为rsinφdθ,径向方向的高为dr.从而选取体积微元
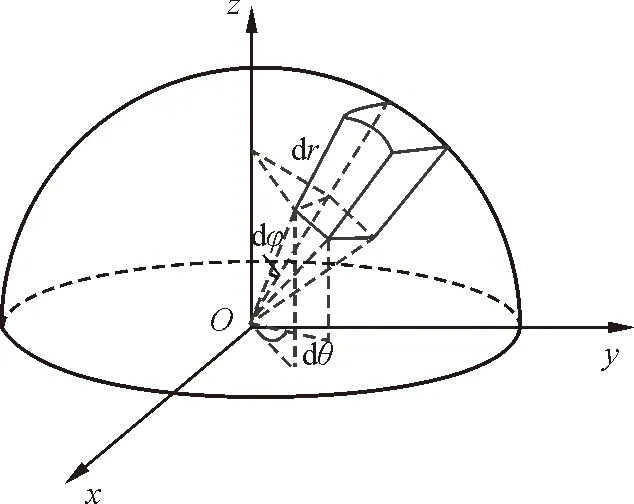
图4 半球体可看作无穷多个曲面六面体
dV=r2sinφdθdφdr
则质量微元[1]
dm=ρr2sinφdθdφdr
对其积分
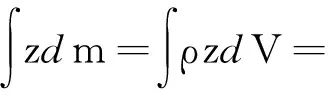
与式(1)联立,从而得到
3.4 薄圆盘高度取dz
如图5所示,半球体可看作无穷多个薄圆盘,圆盘的底面积为Sz,圆盘的高为dz,选取体积微元为dV=Szdz,如图5所示.
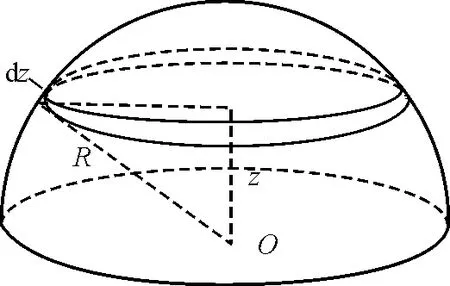
图5 半球体可看作无穷多个薄圆盘
由几何关系,有
Sz=π(R2-z2)
则质量微元
dm=ρπ(R2-z2)dz
对其积分
与式(1)联立,从而得到
3.5 薄球壳厚度取dr
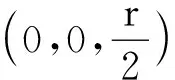
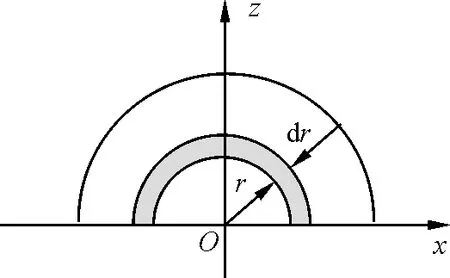
图6 半球体可看作无穷多个薄半球壳
(2)
因此可以对无穷多个薄半球壳进行如下微元选取和积分.
对应体积微元dV=2πr2dr,则质量微元
dm=2πρr2dr
对其积分
将式(2)代入上式,得
与式(1)联立,从而得到
4 结论
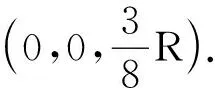
通过上述5种微元选取的方法,了解了在积分过程中微元选取方法的多样性,亦即计算物体质心位置方法的多样性,在具体问题中,可以视微元选取的简便性采用不同的微元取法.
但我们知道,微元的选取方法远不止上述5种,质心位置的计算方法也不仅如此,在具体计算中,还可以借助一些转换[2]来简化计算和拓宽思路.
在大学物理的学习过程中,微元法作为一种广泛的分析方法,在计算物体的质心位置、转动惯量、非保守力做功、电场和电势的分布、稳恒电流的磁场分布等问题中都有涉及.因而需要用到不同的微元法对问题进行分析,这也是我们讨论多种微元选取方法的意义所在.

