手术机器人万向关节组的正逆运动学分析

姜文军, 吕东波, 陈正隆, 李晓贞

(安徽科技学院 机械工程学院,安徽 凤阳 233100)

随着医疗技术的不断提升,手术机器人逐步在手术医疗中推广使用,万向关节组作为手术机器人的重要组成部分,具有重要研究意义[1-3]。因万向关节组具有较好的运动性和灵活的自由度,在手术机器人中应用非常广泛[4-5]。然而,目前关于万向关节组的研究很少考虑到正逆运动学的问题,导致关节组无法精准控制[6-7]。因此,本研究提出一种新的正逆运动学分析方法,使万向关节组的运动更加稳定。

正运动学和逆运动学是机械臂运动学的核心问题,一般使用D-H参数法[8]和齐次坐标法[9]解决该问题。1995年Denavit和Hartenberg首次提出了D-H参数法,通过在机器人的各关节连杆上建立坐标系,得到相邻关节连杆之间的位置姿态变换关系,最终推导出末端关节连杆相对于基座关节连杆的位置姿态。D-H参数法分为标准D-H参数法和改进D-H参数法。目前常用分析方法为标准D-H参数法,但实际使用中标准D-H参数法还存在很多问题,导致无法针对所有关节连杆进行建模、建立的机器人模型与实体不一致以及无法进行局部关节位置分析等问题,其应用场景和计算结果与改进D-H参数法相比,存在局限性[10-13]。

本研究采用改进D-H参数法对手术机器人万向关节组的正逆运动学进行研究。通过分析研究,正运动学的解唯一,逆运动学的解往往不唯一且分析过程复杂[14-15]。通过建立运动学模型,并计算正逆运动学模型结果,所建立的模型符合应用要求,可为同类型手术机器人机械臂及万向关节组的运动学研究提供参考[16-17]。

1 正运动学分析

1.1 齐次坐标法

万向关节组由多个相同类型的球关节串联而成[18],其中基座关节作为关节组基座,用于连接在机架上的固定件,末端关节作为末端执行器基座,用于连接末端执行器和关节组,末端关节和中间关节可以绕着各自的旋转中心做万向运动(图1)。关节组采用绳驱动作为驱动方式,操控手柄与万向关节组通过高强度绳索连接驱动,即操作者在手术腔镜的配合下,根据需要位移的实际工作量活动操控手柄,实现关节组的精准位移,避免出现关节组位移距离、角度偏差等情况,从而保障万向关节组运动的稳定性。根据力矩平衡条件可知,在关节组发生弯曲时,关节组中每个关节的运动具有一致性,所以对相邻的2个关节进行运动分析即可叠加出整体关节组的运动情况。

将关节模型简化为数学坐标模型,将坐标系建立在每个关节的旋转中心处,设D为关节i-1的坐标原点Oi-1到与关节i的坐标原点Oi之间的距离,当关节发生偏转后,把相邻的2个关节之间坐标系的变化看成坐标系通过平移和旋转变换后得到的新坐标系,这样就将复杂的万向运动转换成多步骤的简单运动[19]。

由图2可知,当相邻关节发生运动,相对固定的坐标系原点Oi-1与移动后的坐标系原点Oi之间的平移部分可以看成3个部分的组合:沿Xi轴方向移动线段Oi-1Q的长度、沿Yi轴方向移动线段QW的长度、沿Zi轴方向移动线段WOi的长度。

根据几何关系,将平移部分转换为已知量D的三角函数,记sθ=sinθ,cθ=cosθ,sφ=sinφ,cφ=cosφ,通过齐次坐标法转换成平移矩阵T:

(1)

分析数学坐标模型可知,坐标系的旋转部分可拆分为绕Xi轴和Zi轴的旋转矩阵的乘积,其中坐标系绕Xi轴旋转的角度为θ,绕Zi轴旋转的角度为φ,依照右手坐标系建立旋转矩阵Rx(θ)和Rz(φ),根据旋转部分的顺序,按照矩阵的运算法则得到总的旋转矩阵R:

R=Rz(φ)×Rx(θ)×Rz(-φ)

(2)

综合式(1)、(2)得到相邻的关节i与关节i-1的坐标变换矩阵A为:

(3)

因为关节组中每个关节的运动具有一致性,所以末端关节y相对基座关节x的坐标变换关系等于矩阵A的y-x次方,即齐次坐标法正运动学方程C为:

C=(A)y-x

(4)

选择1组万向关节组的基本参数,其中D=2.9,θ=π/12,φ=π/9,在Solidworks软件中建立相应的简易关节模型,在装配体中将关节模型按照相应的配合关系进行定义,如图3所示,得到末端关节相对基座关节的位置坐标为(2.31,6.35,8.81)。在Matlab软件中将式(4)封装为函数,将选定的基本参数带入函数,得到计算结果如下:

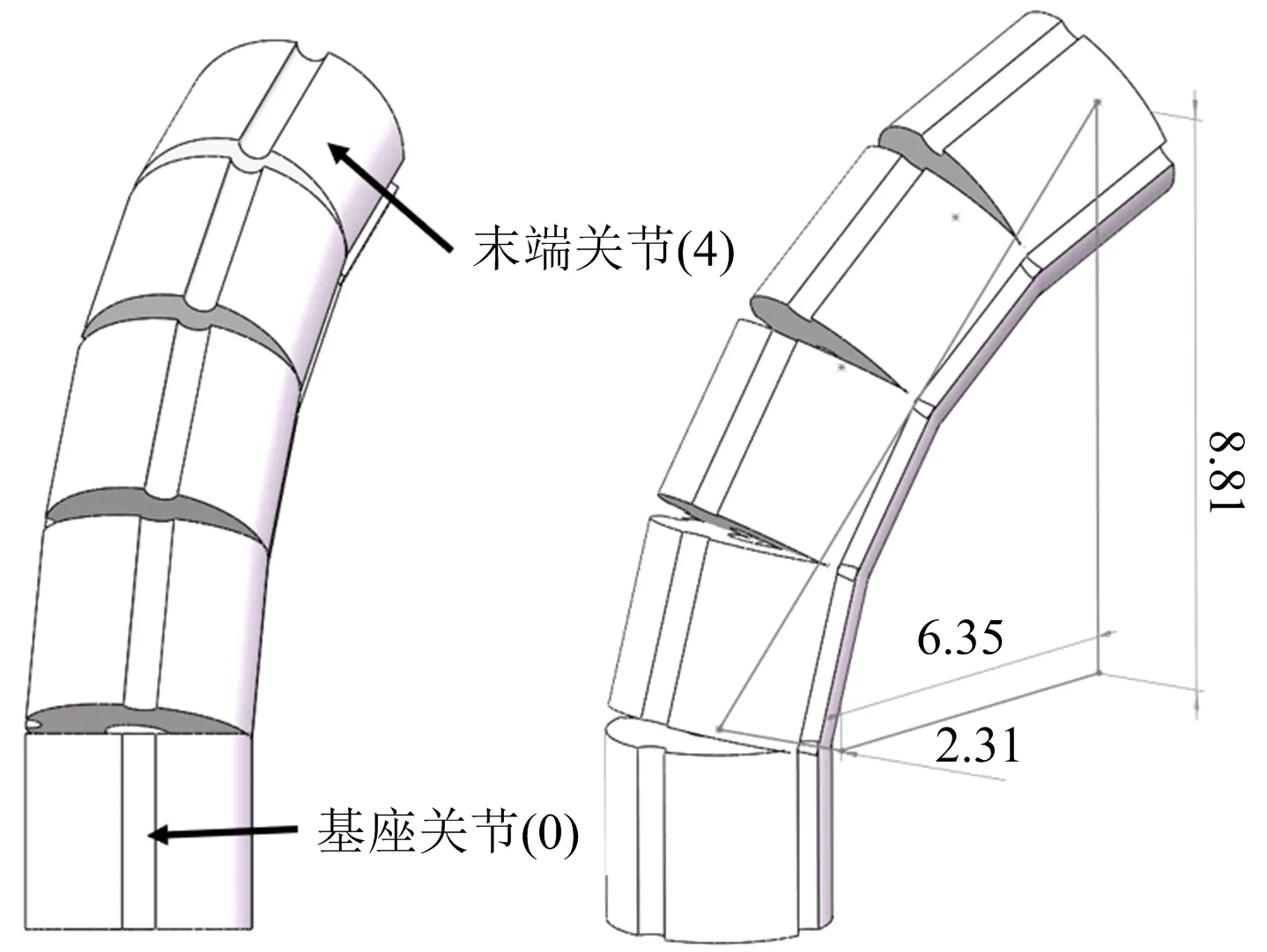
图3 Solidworks模型Fig.3 Solidworks model

(5)

由图3和式(5)中矩阵C的第4列元素得知,齐次坐标法建立的正运动学方程和Solidworks模型得到的末端关节相对基座关节的位置坐标相同,即齐次坐标法正运动学方程建立正确。

1.2 D-H参数法

D-H参数法是一种对机器人运动学分析的通用方法,通过将机器人简化为关节和连杆的组合,从而把X轴、Y轴、Z轴的平移和旋转替换成关节与连杆的角度和距离,达到将6个变化元素变成4个变化元素、简化求解过程的目的。D-H参数法分为标准型和改进型:标准D-H参数法是将坐标系建立在连杆的输出关节上,即连杆i后的关节i+1;改进D-H参数法是将坐标系建立在连杆的输入关节上,即连杆i前的关节i。当机器人出现树状结构时,1个连杆对应多个输出关节,标准D-H参数法容易出现错误,所以使用改进D-H参数法分析关节组的运动学。根据D-H参数法的定义,关节分成转动关节和移动关节,设θ为转动关节的关节变量。d为移动关节的关节变量。改进D-H参数法相邻关节i(i=1～6)之间的变换总结为:αi为绕Xi轴Zi到Zi+1的旋转角度;ai为沿Xi轴Zi到Zi+1的距离;di为沿Zi轴Xi-1到Xi的距离;θi为绕Zi轴Xi-1到Xi的旋转角度。

1.2.1 组合式运动模型的建立 根据D-H参数法的定义,设θ为转动关节的关节变量 ,d为移动关节的关节变量。相邻关节之间的变换可以总结为:αi为绕Xi轴Zi到Zi+1的旋转角度;ai为沿Xi轴Zi到Zi+1的距离;di为沿Zi轴Xi-1到Xi的距离;θi为绕Zi轴Xi-1到Xi的旋转角度(表1)。通过对万向关节组运动形式的分析研究,将万向运动看成2个方向上转动关节的组合,即关节1和关节2的坐标系原点重合且旋转轴互相垂直,由此建立组合式运动模型。如图4所示,在组合式运动模型上建立改进D-H参数法的坐标系,因为关节1的坐标系原点O1和关节2的坐标系原点O2重合,所以连杆1不存在,且关节组中全部都是转动关节,所有坐标系的X轴在同一平面中,根据参数定义方法,a1=0、di=0,得到关节组所有的D-H参数。组合式运动模型的建立,可以直观地表示万向关节组的运动模型结构,同时根据参数定义方法得到关节组所有的D-H参数,为后续的正逆运动学方程建立、运算及验证提供基础运动模型依据。

表1 D-H参数表

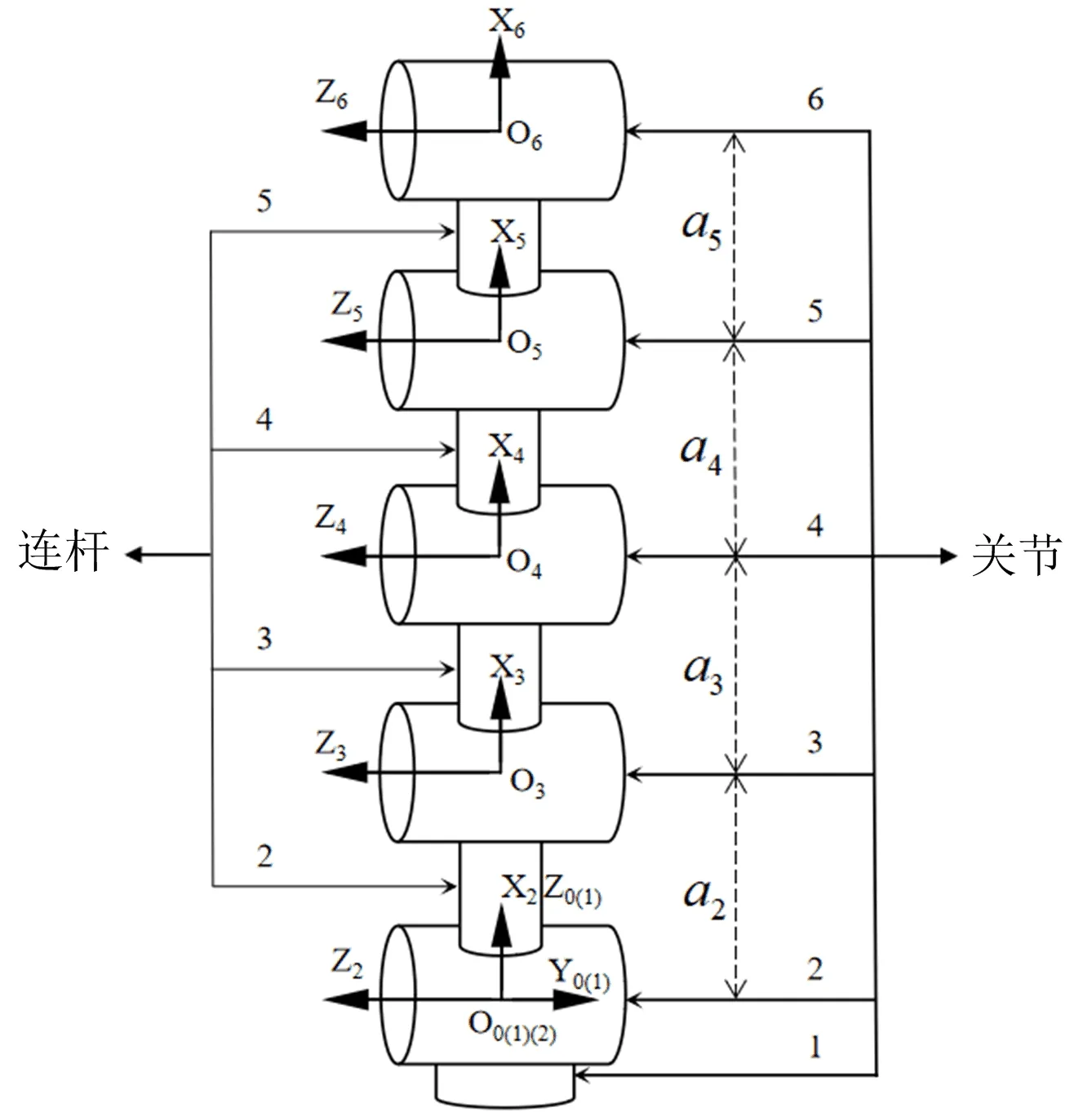
图4 组合式运动模型Fig.4 Combined motion model

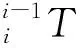
(6)

将表1中的D-H参数带入式(6)中,得到每个相邻关节间的D-H变换矩阵:

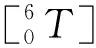
(8)

1.2.3 正运动学方程的验证 根据表1的D-H参数,在Matlab软件中的Robotics Toolbox工具箱建立1个串联类型机器人,通过赋予机器人关节旋转角度(-11π/18、7π/12、π/12、π/12、π/12、π/12),得到机器人整体姿态和末端位置(图5)。在Matlab软件中将式(8)封装成函数,将表1的D-H参数带入得到计算结果如式(9)所示。由图5和式(9)中矩阵T的第4列元素得知,改进D-H参数法建立的正运动学方程和Robotics Toolbox工具箱中建立的机器人模型得到的位置坐标相同,即改进D-H参数法正运动学方程建立正确。

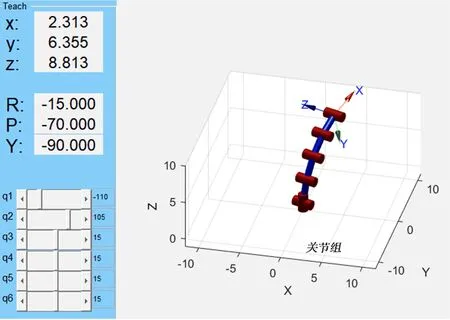
图5 弯曲的关节组机器人Fig.5 Bved joint group robot

(9)

2 逆运动学分析

目前学术界对逆运动学有2种主流解法:一种是基于D-H参数法正运动学方程求逆的解析法;另一种是基于雅可比矩阵的等效微分法。解析法的优点是可以直接得到逆运动学方程,在分析计算、封装函数方面存在优势,缺点是可能存在多种解;等效微分法的优点是可以得到唯一解,但解析过程复杂[20]。本研究中逆运动学分析是为了验证正运动学方程的正确性,结合实际采用解析法作为求解思路,并用代入消元法进行结果的求解计算[21]。

2.1 逆运动学方程的建立

解析法是基于正运动学方程反向求解的方法,求解思路是对由若干D-H变换矩阵构成的正运动学方程等式左右同时进行矩阵变换,进而在等式左右得到新的矩阵,最后将等式左右新矩阵内的元素一一对应成方程组,通过代入消元法计算方程组,从而求解出方程组中的D-H参数。

将改进D-H参数法得到的正运动方程改写为未知量矩阵的形式:

(10)

(11)

将式(11)左右两边分别进行运算,并将得到的2个4×4新矩阵中对应位置的元素提取出来建立方程,得到1个拥有16个方程的方程组,筛选删除重复计算或计算难度大的方程,剩下由5个方程构成的方程组就是建立的逆运动学方程:

nycosθ1-nxsinθ1=0

(12)

aycosθ1-axsinθ1=-1

(13)

nz=sin(θ2+θ3+θ4+θ5+θ6)

(14)

oz=cos(θ2+θ3+θ4+θ5+θ6)

(15)

pz=a2sinθ2+a3sin(θ2+θ3)+a4sin(θ2+θ3+θ4)+a5sin(θ2+θ3+θ4+θ5)

(16)

2.2 逆运动学方程的验证

分析发现式(12)、(13)中只有1个未知量θ1,符合代入消元法的定义。式(13)适用于高等三角函数公式中的辅助角公式f(x)=asinx+bcosx=c在a2+b2=c2的特殊情况,将式(13)带入辅助角公式求解,并计算式(12)可得:

(17)

综合式(17)得θ1=-11π/18。

为方便计算,设θa=θ2+θ3+θ4+θ5+θ6,因为关节组的每个关节运动具有一致性,且关节间的连杆长度一致,设a=a2=a3=a4=a5,θ=θ3=θ4=θ5=θ6,将参数θa、a、θ带入式(15)、(16)可得:

(18)

综合式(21)、(22)得θa=θ2+4θ=11π/12,将计算结果带入式(17)可得:

(19)

将式(19)通过三角函数的倍角公式等运算公式计算,结合上文计算结果可得:

(20)

通过对逆运动学方程的求解,解出各关节的旋转角度θi,根据式(17)、(20)得知计算出的旋转角度θi与D-H参数表中给定的关节变量θi一致,也与通过Robotics Toolbox工具箱中的求逆函数(ikine)求解出的结果之一相同,表示逆运动学方程求解正确,也验证了正运动学方程的正确性,求解结果证实关节组的运动距离、角度的理论值与实际的结果一致,通过绳驱动的关节组不会出现位移量、角度偏差等情况,万向关节组确保在给定轨迹上运动。正逆运动学方程的建立可以帮助万向关节组实现轨迹规划、跟踪以及处理限制和约束等目的。万向关节组能够在给定轨迹上运动,帮助关节组实现精准到达目标位置,验证万向关节组运动的稳定性。

3 结论

本研究以手术机器人万向关节组作为研究对象,对其运动学进行研究分析。首先分别采用齐次坐标法和改进D-H参数法,通过推导末端关节坐标系相对于基座关节坐标系的位置姿态。建立2个关节组正运动学方程;其次采用代入消元法,通过改进D-H参数法建立的正运动学方程变形建立逆运动学方程,并进行逆运动学分析计算;最后通过Solidworks、Matlab软件对3个正逆运动学方程进行运动学仿真分析和数据验证。

仿真和计算结果表明2个正运动学方程计算的末端关节位置相同,逆运动学方程计算的关节角度和D-H参数表中一致,得到了1种新的正逆运动学计算方法。通过对比,证实本研究中关节组运动学方程构建正确,验证了正逆运动学计算方法的有效性和万向关节组运动的稳定性。为万向关节组运动控制的研究奠定了基础,此研究结果可以为同类手术机器人关节组研究提供参考依据。