北京某办公建筑竖井热压通风效果测试与分析*

郑 坤 徐 伟 李安桂 宋占寿 韩武松 赵 刚 郭 然 褚俊杰 王烁焱

(1.中国建筑设计研究院有限公司,北京;2.西安建筑科技大学,西安;3.中国建筑科学研究院有限公司,北京)

0 引言

建筑热压通风技术是大型复杂建筑自然通风的主要手段,竖井通风是其常见方式之一[1-5],国内外学者对此进行了广泛的研究。克鲁姆等人介绍了建筑物热压自然通风的原理[6]。针对不同的竖井热压通风系统,研究人员提出了顶部和底部对外开口、侧面对室内开口的竖井热压流动的定量模型[7],上层热压流动驱动下层自然通风流动模型[8],竖井侧面连续开缝和竖井侧面连续开缝与上部同时开口的竖井中和界位置的多区域模型[9],多层建筑竖井热压通风的简化数学模型[10],评估竖井烟囱效应的数学模型[11],上部机械通风下部自然通风的复合通风模型[12],烟囱内流动模型[13-14]等。可见,建筑热压通风理论研究较多,缺少对实际项目竖井热压通风系统运行效果的测试与分析。

为了验证竖井热压通风的效果,本文对北京某办公建筑进行了测试。该办公建筑总建筑面积4.1万m2,地上面积2.2万m2。地上共15层,地下5层(含夹层),建筑高度60 m。主要功能为办公及其配套用房。建筑1～10层北侧有阶梯式裙房,裙房北侧围护结构处设有高大的斜中庭,外立面见图1。为了加强过渡季和夏季夜间自然通风,核心筒办公南区中部设置拔风竖井,利用室内热源形成的热压驱动室内自然通风。考虑中和界的位置,在3～8层设置进风百叶,屋面竖井出口四周设置排风百叶[15]。

图1 建筑北向外立面图

在方案设计阶段,曾探讨在竖井内设置太阳能热水换热系统强化热压通风。经过模拟计算,换热器增大了竖井内空气流动阻力,且热压增量无法抵消阻力,故未设置太阳能换热装置。另外,为实现各层均匀自然通风,各层开口面积应由低层到高层逐层增大[5]。

1 竖井热压通风系统

1.1 竖井热压通风原理

竖井热压通风的驱动力来自竖井内空气与室外空气的密度差[16],见式(1)。相对于竖井上只有2个开口的系统,多层或高层建筑的多开口竖井系统热压驱动力形成的原理更加复杂。首先,中和界的位置随竖井开口开启数量和面积的变化而移动,进而影响各层开口处余压,各层进风量随之变化。其次,各层室内热源散热量不同,室外空气被加热后进入竖井的温度不同,造成竖井内空气流动情况复杂,井内竖向空气温度,即热压驱动温度分布不明确。

Δp=gh(ρw-ρn)

(1)

式中 Δp为热压,Pa;g为自由落体加速度,m/s2;h为竖井高度,m;ρw为室外空气密度,kg/m3;ρn为竖井内空气密度,kg/m3。

竖井热压通风系统的空气流动路径是从室外进入室内,再进入竖井,在竖井内向上流动排出,竖井热压通风系统示意图见图2。因此,整个路径的阻力部件包括外窗、室内家具、竖井开口百叶、竖井和屋面出口百叶,所有阻力均由热压克服。该系统比中庭等大空间空气热压流动的阻力部件更多,其能量公式更复杂,简化计算原理见式(2)。

图2 竖井热压通风系统示意图

(2)

式中m为系统局部阻力部件数量;ζi为部件局部阻力系数(包括外窗、百叶和竖井汇流处);vi、vj为空气流速,m/s;ρi、ρj为空气密度,kg/m3;n为系统沿程阻力部件数量;λj为摩擦阻力系数(包括竖井和室内家具等效沿程阻力);De为竖井当量直径,m。

1.2 物理参数

受限于具体使用情况,该建筑仅可以开启第4～6、8层的竖井东侧进风百叶。竖井截面尺寸为2.80 m×2.50 m,混凝土刷白。百叶材质为铝,各层进风百叶角度可调节,尺寸分别为1.50 m×1.20 m、1.50 m×1.20 m、1.80 m×1.20 m和1.85 m×1.40 m;竖井出屋面处侧面百叶角度为固定向下倾斜45°,北面和南面百叶尺寸为3.60 m×1.30 m,西面和东面百叶尺寸为2.40 m×1.30 m。测试各层的建筑使用面积分别为:4层1 200 m2,5层1 150 m2,6层930 m2,8层720 m2。

2 测试方案

为了获得过渡季竖井热压自然通风的效果和消除冬季热压自然通风的副作用,分别于2021年10月10—13日和2022年1月27—28日进行了过渡季和冬季典型点位的温湿度和风速测试。使用仪器包括温湿度自记仪若干、手持热线风速仪1台,仪器均经过校正并在有效期内,测试仪器参数见表1。

表1 测试仪器参数

以4层为例,其测点布置见图3。温湿度自记仪设置于室外(点4W)和室内典型位置(点4C和4D),同时考虑进风百叶竖向温度梯度,均匀设置2个测点(点4A和4B)。温湿度自记仪初始设置记录时间间隔为5 min,既满足测试值准确性要求,又满足测试总时间的待机时长。同时使用手持热线风速仪测试斜中庭内竖向风速(点4f),目的是利用中庭的均压作用减小室外风压的影响,保证测试效果主要体现热压作用。另外,为计算进风量,测试百叶上5个均匀分布点(点4a～4e)的风速,以其平均值代表百叶进风风速,测试风速的同时记录测试时间。

图3 4层测点布置

3 热压通风竖井作用下不同季节测试与分析

3.1 过渡季温度和进风百叶风速分布规律

笔者于2021年10月10日开始布置测试仪器,由于过渡季驱动热压通风的温差较小,每次测试需待空气流动稳定后进行。在测试期内共进行了10个工况的测试,各工况进风百叶开闭状况和测试时间见表2,其中工况4～6进风百叶角度为45°,其余工况为90°。另外,由于需测试的实验数据众多,难以实现同时测试各层测点,因而采用依次测量的方法。这就导致室外温度在各个工况下并不一致,为了排除其影响,对温度进行量纲一处理。

表2 测试工况进风百叶开闭状况和测试时间

(3)

式中T为量纲一温度;tn为室内测试温度,℃;tw为对应时刻室外测试温度,℃。

经测试,各层测点温度随时间的变化规律具有一致性,取各层测点温度平均值进行比较,如图4所示。各测试工况的进风百叶平均风速如图5所示。

图4 过渡季各层温度测试数据

观察图4,发现8层量纲一温度在各个工况都较高,即室内温度相较室外更高,最高点温度相比室外升高了54%。原因可能是8层工作人员较多、散热量较大,或是热压通风量较小、降温能力弱,从而提高了室内温度。图4中,工况1、3、6、9、10整体温度都偏低,工况2、4、5、7、8整体温度都偏高,分析原因是前者测试时间为15:00左右,此时室外温度较高,后者测试时间为10:00和19:00左右,此时室外温度较低。

图5中,进风百叶平均风速为1.1～2.5 m/s,且下层风速高于上层。百叶开度变小,4层风速增大,但5层和6层风速却并无明显变化,8层反而风速减小。工况7～10关闭了上层部分百叶风口,并没有对下层百叶风速造成影响。百叶开度变化和开闭状况并未对各层风速造成规律性影响。

3.2 冬季温度和进风百叶风速分布规律

笔者于2022年1月27日开始进行测试,使用的仪器和测点布置同过渡季。由于测试总时间较过渡季短,温湿度自记仪初始设置记录时间间隔为2 min。冬季驱动热压通风的温差较大,进风量大,会引起人员不舒适,但其驱动温差的日波动较小,空气流动易于稳定。综合考虑以上因素,各工况进风百叶开闭状况和测试时间见表2。温度值仍然选择量纲一温度,测试结果见图6、7。可见,各层相同位置测点同一天的量纲一温度较稳定,且第二天的测试温度高于前一天。同一天不同位置测点各层温度变化不大,室内温度分布较均匀。进风百叶平均风速为3.3～4.7 m/s,下层风速高于上层,且明显高于过渡季。

图7 冬季进风百叶平均风速

由上述分析可知,室内温度是室内热源、室外温度和通风量综合作用的结果。进风百叶风速与进风量直接相关,而进风量又受室内外温差的影响。须在后文进一步探究找出竖井热压通风多因素之间的耦合及作用关系。

4 竖井百叶不同季节进风量及其影响因素分析

4.1 过渡季百叶进风量

根据进口百叶平均风速和有效面积,可以得到不同测试工况下各层竖井百叶进风量,过渡季各工况百叶进风量见图8。

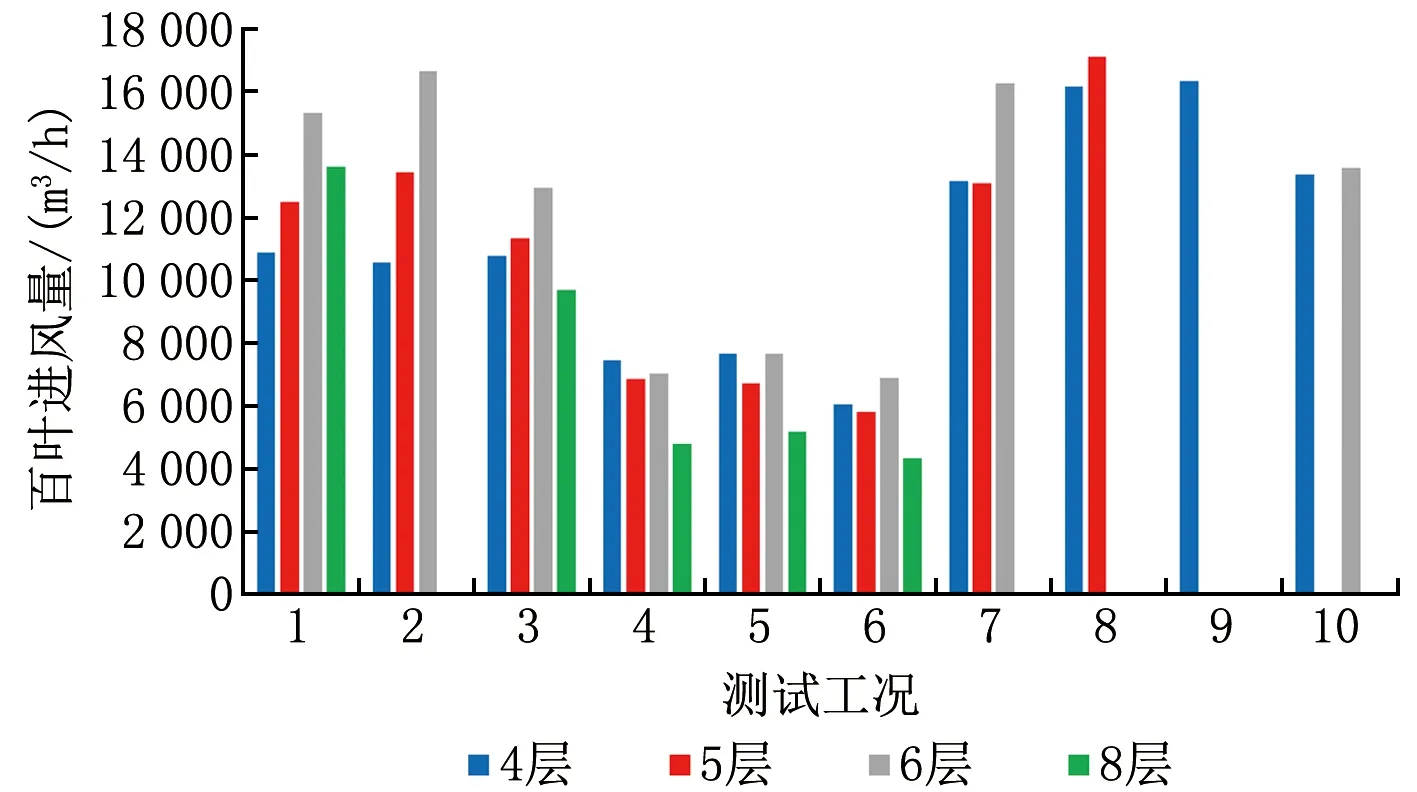
图8 过渡季百叶进风量

从图8可见,百叶开度均为90°时,工况9的4层进风量为16 323 m3/h,工况10的4层进风量为13 364 m3/h,工况7的4层进风量为13 159 m3/h,工况3的4层进风量为10 773 m3/h。随着开口数增多,中和界下移,百叶处余压减小,从而进风量减小。同一工况,各层百叶进口空气温度不同,驱动温差不同,风量变化趋势一致,均为先增大后减小,变化量不大。工况1～3中,4层热压最大,但其进风量略小于5、6层,表明竖井内阻力不能忽略。调节百叶角度(由90°调节至45°),进风量减小明显,进风百叶阻力对风量影响较大。

4.2 冬季百叶进风量

与过渡季的数据处理方法一样,得出不同测试工况下各层竖井百叶进风量,冬季各工况百叶进风量见图9。从图9中可见,各层进风量较过渡季大幅增加,并呈现底层高上层低的趋势,不同工况下同层的进风量相差不大。由于在同一工况中未开启多层百叶和调节进风百叶角度,无法得出竖向各层风量的关系和百叶阻力对进风量的影响。

图9 冬季百叶进风量

4.3 竖井内中和界位置与驱动温度分析

为了得到热压通风的驱动温度,并且探究竖井热压中和界位置的变化规律,笔者对通风竖井典型测试工况(过渡季工况3、4、7～10和冬季工况1～4)做了数值模拟。

4.3.1计算模型

通过计算,竖井内气流运动的雷诺数在7 664～5.25×105之间,因此竖井内气流运动可认为是湍流,假定内部空气运动稳定且不可压缩,对应湍流模型选择K-ε模型[17]。同时考虑竖井内空气温度变化对浮升力的影响符合Boussinesq假设。本研究以竖井通风稳态过程为主,综合考虑精确度和收敛速度,选择SIMPLEC算法。收敛准则设置为湍流项残差值小于10-4,能量项残差值小于10-6。

4.3.2网格独立性验证

网格数对模拟计算结果的准确性有直接影响。为验证本模型的数值模拟结果与模型网格数无关,采用不同的网格划分方式,对3种不同网格数的模型(网格数分别为1 222 350、2 444 700 和3 873 240)进行CFD计算及结果对比分析。不同网格数的速度和温度分布结果如图10所示,可以看出,不同网格数的速度和温度偏差较小,速度和温度的平均偏差分别为0.70%、0.29%。综合考虑模拟计算效率及成本,本文选取网格数为2 444 700 的模型进行模拟计算。

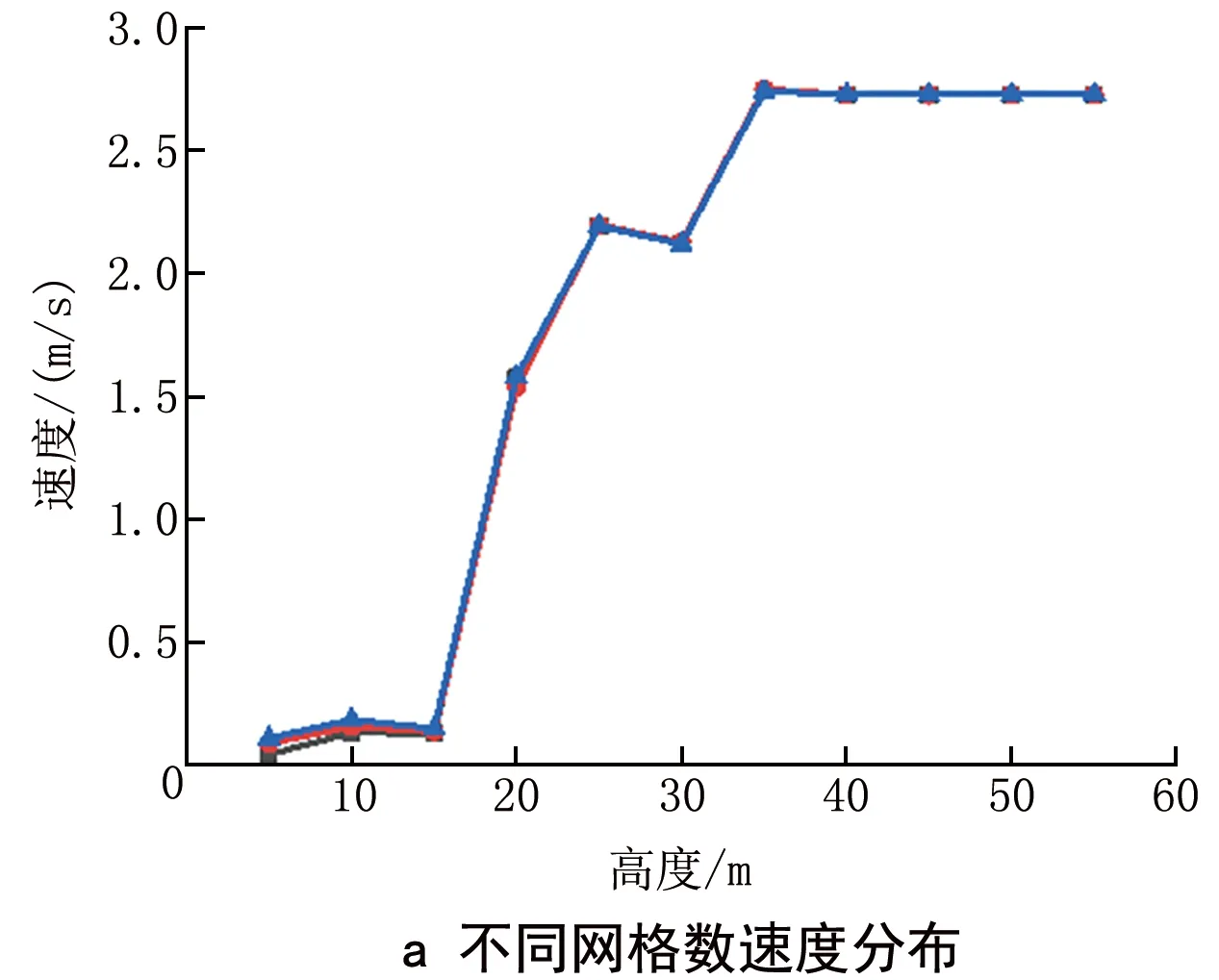
图10 网格独立性检验

4.3.3边界条件设置

考虑到本研究为竖井内部热压作用下的气流运动,竖井开启的楼层进风口定义为速度入口(velocity-inlet),数值来源于实测数据;竖井出口定义为压力出口(pressure-outlet)。竖井出口和进口建模中均考虑了实际尺寸和百叶遮挡。竖井在建筑内区,不考虑竖井墙体对竖井内空气的传热影响,因此墙壁设置为光滑绝热墙体(wall)。

4.3.4模拟结果

限于篇幅,仅呈现过渡季工况4和冬季工况1的模拟结果云图(见图11和图12)。

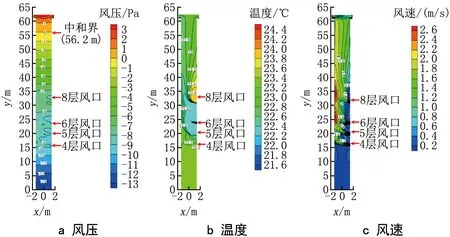
图11 过渡季工况4模拟结果云图

图12 冬季工况1模拟结果云图

模拟结果显示,过渡季工况3、4、7～10和冬季工况1～4的中和界高度分别为48.6、56.2、49.1、52.5、59.5、56.9、56.5、53.7、54.3、57.0 m。中和界位置随着百叶开启层数增多、百叶开启面积增大、进风量增大而下移。过渡季中和界位置越高,下部可以开启百叶进行自然通风的层数越多,但各层应按需控制百叶开启角度,使中和界位置上移而增加通风层数。冬季竖井热压通风会带来额外的冷风渗透负荷,导致建筑外区人员不舒适,应避免开启进风百叶。冬季竖井中和界位置较高,但压力梯度和过渡季相比并无较大增加。因此,采用气密性好的进风百叶,冬季关闭就可以阻断自然通风。在超高层建筑或严寒地区的高层建筑中,热压梯度增大较多,可以在竖井百叶外增加阻力部件,例如设置带气密性较好内门的小隔间,冬季关闭内门克服竖井热压作用。

由图11可见,过渡季各层进入竖井的空气温度和速度不同,造成竖井内空气流动情况复杂,各层热压驱动温度和进风温度不完全一致。一般可以百叶中心高度竖井横截面的平均温度代表驱动温度,4～6、8层分别为23.2、22.7、22.4、22.9 ℃,并未呈现文献[18]中给出的温度梯度规律。究其原因,可能因为竖井内空间局限,空气流动未充分混合,造成同层温度不均匀,竖向无分层。

5 过渡季竖井热压自然通风效果分析

在方案阶段,根据所采取的竖井方案的模拟计算结果,3～8层的自然通风换气次数为6.2～7.4 h-1,室内温度为25.2～26.5 ℃,可以同时满足过渡季自然通风的新风量和热舒适要求[5]。按本文设定的设计工况(参数见表3),由式(4)[19]计算得出消除室内余热所需室外空气温度与人均新风量的关系,并拟合出关系式,见图13。以设计最小人均新风量30 m3/h为例,消除余热所需室外最高温度为9.3 ℃。随着人均新风量的增加,消除室内余热所需的室外空气温度趋于稳定,约为23 ℃。换言之,当室外空气温度上升到23 ℃以上时,增大风量已经不能消除室内余热。

表3 过渡季设计工况参数

图13 设计工况消除室内余热所需室外温度与人均新风量的关系

(4)

式中G为消除室内余热所需新风量,m3/h;Q为室内余热,kW;c为空气比热容,kJ/(kg·℃),c=1.0 kJ/(kg·℃);tp为排风温度,℃,采用百叶进风平均温度。

在设计人数和各工况实测风量下,为消除室内余热,可以按上述拟合关系式计算出需要的室外温度,再判断测试时的室外温度是否满足需求。以4层为例,其热压通风效果如表4所示。进风百叶角度为45°时均不能满足需求;进风百叶角度为90°时,室外温度在18 ℃以下均满足需求。

表4 过渡季竖井热压通风效果

笔者为了研究测试工况可消除室内余热时对应的室内人数,将此人数表述为“计算在室人数”,结果如图14所示。由图14可知,各工况计算在室人数均小于设计人数,若按设计人数进行各层人员配置,几乎都无法消除室内余热。实际使用时,在室人数一般小于设计人数。所以在竖井热压通风系统实际运行时,不应以满足设计工况所需的室外温度作为开启进风百叶的依据,而应该监测实际在室人数,测算出可以排除余热的室外温度作为百叶开启的条件,此时的通风量还应大于人员最小卫生新风需求。这样的运行策略才能最大限度地发挥竖井热压自然通风的节能潜力。

图14 各工况计算在室人数

6 结论

1) 竖井热压通风系统热压驱动力形成原因复杂,阻力部件多。在过渡季和冬季测试了进风温度和风速,结果显示,室内温度是室内热源、室外温度和通风量综合作用的结果。

2) 对过渡季和冬季竖井百叶进风量进行分析得出,竖井热压通风系统中影响进风量的因素较多,主要有驱动温差和系统阻力。其中,冬季和过渡季的驱动温差变化引起进风量变化较大,进风百叶阻力占系统总阻力权重较大,竖井内阻力不能忽略。

3) 分析了影响竖井内中和界位置的因素,提出了过渡季优化利用热压通风降温和冬季消除热压通风副作用的方法。

4) 模拟结果显示,竖井内热压驱动温度同层不均匀,竖向无分层。竖井内热压驱动温度分布规律仍待进一步研究。

5) 过渡季室外温度变化较大,满足室内热舒适的计算在室人数随之变化。本文提出了随实际在室人数变化的动态调整百叶策略,最大限度地发挥该系统的节能潜力。