竹材索道集材运输装备跑车及悬索的设计与分析

雷永杰，周建波，傅万四，冯海韵，傅 兴，王凡雨，张立忠，张雨晴，廖新华

（1.国家林业和草原局 哈尔滨林业机械研究所，黑龙江 哈尔滨 150086；2.中国林业科学研究院 木材工业研究所，北京 100091；3.北京海垦商贸发展有限公司，北京 100028；4.长沙正忠科技发展有限公司，湖南 长沙 410116）

中国竹林面积大，竹材资源丰富。据统计，2022 年中国竹林面积高达709.92 万hm2，但由于竹子主要分布在海拔200～1 200 m[1]，受竹林立地条件和林道建设滞后制约，将竹子从山上采伐运输出来十分困难。长期以来，人工砍伐竹材后，通过人力或畜力将竹材运至山下，生产方式落后，劳动强度大、效率低[2]。为降低劳动强度，有人把钢丝绳作为运送索道来实现快速运竹，但运送索道前期布置比较困难，且对悬索和跑车的使用寿命及安全要求较高[3]。当前，中国林业索道集材领域跑车主要分为无动力源和自带动力源两大类。无动力源跑车不具备自主起吊或装卸货物的能力，此类索道装卸货物需人力或其他外力，功能单一，效率不高。自带动力源跑车可起吊和自主装卸货物，但此类跑车机械结构复杂，质量大，且因蓄电池容量限制，跑车的续航能力不足，若在工作途中蓄电池电量耗尽，易导致运输过程发生货物掉落等安全事故[4]。如何将采伐的竹材高效安全、低成本运输下山成为亟待解决的技术瓶颈。

本研究对竹材索道集材跑车运输系统中悬索和跑车等关键部件进行分析，设计了一种结构简单、续航能力强、运输安全性较高的自充电索道跑车，绘制了跑车三维模型，对跑车关键部件进行了有限元分析，对跑车-索道运输系统进行了仿真试验。自充电跑车设计大幅提高跑车续航能力和安全性，为竹材运输下山装备开发提供一种新的思路。

1 竹材索道集材跑车运输系统关键部件设计

1.1 基本参数

根据在湖南、福建等省部分竹林地理环境的航拍调研结果，以及竹材质量和结构特点，初步确定竹材索道集材跑车运输系统基本设计参数：竹林垂直高度≤200 m，索道倾斜角≤35°，索道跨距200～500 m，承载索速度≤1.0 m·s-1(可调)，牵引索与回空索速度≤4.0 m·s-1(可调)，跑车质量200 kg，运输跑车单次载质量≤400 kg。

1.2 悬索设计

在现代林业索道集材运输领域中，对工作索的要求为：具有可靠的静态抗拉力和交变的动态承载力；具有良好的抗磨性，在跑车滑轮接触、转动、滑动、挤压作用下不易损耗；具有适宜的弹性，易于吸收冲击。本设计选用“6×19 股纤维芯”钢丝绳作为承载索，根据跑车和吊运质量、索道倾斜角等主要设计参数初步确定承载索规格。承载索金属截面积FMB可由下式计算[5]：

式(1)中：P为总载荷(N)；n为安全系数，对于林业索道承载索，n一般取2；l0为承载索有效长度(m)；β为索道倾斜角；f为有荷最大挠度，f=Sl0，S为有荷最大挠度系数，S一般取0.03；[σ]为承载索钢丝有效强度，[σ]=0.85σb，σb为极限强度，σb=2 160 MPa。总载荷：

式(2)中：Q为跑车与吊运质量(kg)；a为冲击载荷系数，查表取a=0.3。将Q=6 000N代入式(2)可得：P=7 800 N。将P=7 800 N，[σ]=1 836 MPa，最大倾斜角β=35°等参数代入式(1)得：FMB=88.96 mm2。

根据承载索金属截面积，可计算承载索直径(d)：

1.3 跑车设计

1.3.1 结构设计 ①行走机构。行走机构设计的关键是行走滑轮的选择，行走滑轮个数和各滑轮间距大小对承载索弯曲应力影响很大。通过应变片试验测试，行走滑轮作用下承载索弯曲应力分布[5]如图1所示。当跑车吊重在承载索上运行时，行走轮正下方弯曲应力最大，弯曲应力随载荷作用点距离变大而逐渐减小。图1A 比图1B 应力分布情况更加合理，虽然弯曲应力最大值不变，但其弯曲应力的变化曲线较为平缓。因此，任意加大跑车行走轮的间距，对承载索的受力非常不利。为延长承载索使用寿命，应把行走轮布置得相互靠近并使之具有相等的间距。通常行走轮纵向轮距应为行走轮轮径2 倍左右。本设计跑车行走轮间距取700 mm。行走轮个数(N)可由最大弯曲应力( σw)求得[5]：

图1 行走滑轮作用下承载索弯曲应力Figure 1 Bending stress of bearing cable under the action of traveling pulley

式(4)中：P为总载荷(N)；σw为承载索最大弯曲应力(N·mm-2)；Ek为承载索弹性模量(MPa)；T为承载索最大张力(N)；FMB为钢索横截面面积(mm2)。承载索最大张力(T)可由承载索的最大破断拉力(TP)求得：

式(5)中：TP为承载索最大破断拉力，TP=φS，φ为折断系数，φ=0.82～0.90，此处取φ=0.90，S为钢丝绳破断拉力(N)；K为考虑冲击系数后承载索的安全系数，取K=2.5。将TP=100 800 N 代入式(5)，得T=40 320 N，承载索最大拉应力。由式(4)可知：拉应力与承载索张力T成正比，而弯曲应力与承载索最大张力T成反比，考虑到承载索总应力不得超过承载索钢丝绳的有效强度，一般规定：

（五）地缘政治局势依然动荡。当前地缘政治“灰犀牛”“黑天鹅”风险并存。英欧在退欧关税联盟谈判上的对抗性上升，意大利民粹党派几经波折最终成功组阁，西班牙中右翼政府未通过不信任投票，欧洲政治不确定性已对欧元区经济复苏和欧洲一体化发展构成挑战。叙利亚内战、恐怖主义威胁热度难减，伊核问题因美退出协议骤然升温，美驻以使馆迁馆已酿巴以严重冲突，以色列挟美支持对伊朗关系日趋紧张，初显缓和的朝核局势未来走向依然成谜，突发性地缘冲突严重冲击全球经济的风险正在不断积聚。

本次设计取σw=0.5σi=278 MPa。将P=7 800 N，σw=278 MPa，T、Ek和FMB等参数代入式(4)得N=5.3，取N为6 个。②升降卷扬机构。升降卷扬机构指安装于跑车车架底板上对称布置的2 台升降卷扬机，主要包括电机、齿轮减速机构、刹车装置、起重索、防脱挂钩等。通过控制卷扬机起重索的升降实现林间集材和集材点打捆竹材的提升运输。根据索道集材跑车运输系统设计要求，跑车升降卷扬机选用坤航起重机械有限公司生产的迈士顿小型升降卷扬机。卷扬机参数如表1。③自充电机构。自充电机构主要由链传动装置、发电机和蓄电池组成。跑车行走轮在承载索上转动时，前后2 个行走轮通过与其同轴连接的链传动装置将机械能传递给发电机，发电机将转换的电能传输至蓄电池，实现跑车边工作边充电，提高跑车的续航能力。跑车整体结构如图2 所示。

表1 升降卷扬机参数Table 1 Lifting winch parameters

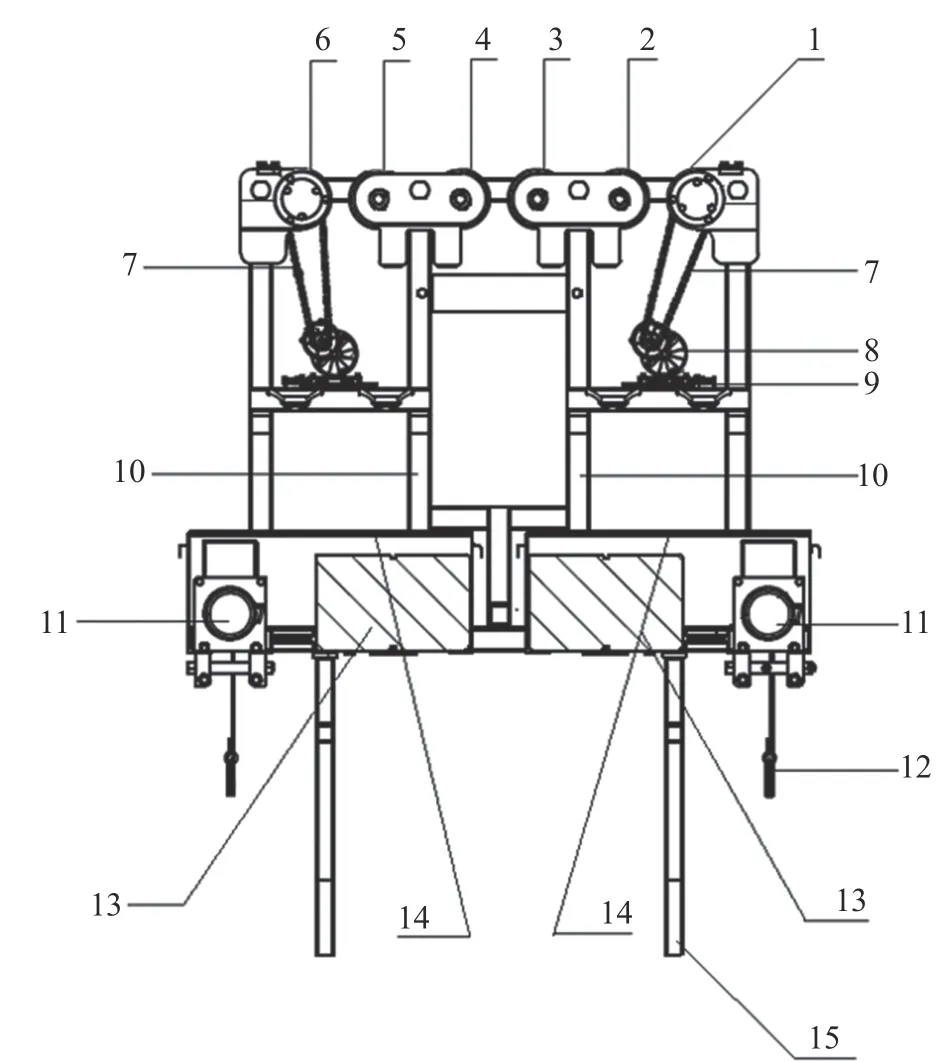
图2 跑车整体结构示意图Figure 2 Overall structure diagram of sports car

1.3.2 工作原理 集材作业时，主机上的卷扬机控制牵引索与回空索运行，牵引跑车在承载索上移动至林间集材点上空，并通过控制牵引索与回空索实现跑车在集材点上空的定位。当跑车固定于林间集材点上空时，用遥控器控制跑车升降卷扬机放索，人工拽拉绳索至林间伐倒竹材处，将卡住竹材根部的卡具挂在绳索上，跑车卷扬机收索，将竹子牵引至林间集材点。在集材点进行竹材打捆，用遥控器控制跑车升降卷扬机收索，提升打捆竹材至限位高度。再控制主机上的牵引索与回空索运行，牵引跑车运输竹材至转运点。

2 跑车行走轮静力学分析

2.1 材料加载与网格划分

由于跑车与重物的整体质量全部通过行走轮支撑在承载索上，行走轮受力较大。若在工作过程中失效，将造成安全事故，所以需对行走轮进行静力学分析[6]。行走轮采用的灰铸铁HT250 制作，其硬度低于钢丝绳。HT250 力学特性如表2 所示。

表2 HT250 材料特性Table 2 HT250 material properties

利用ABAQUS 自带的四面体网格法[7]对行走轮进行网格划分。图3 为网格划分图，网格节点总数为247 062 个，单元数为82 354 个。

图3 行走轮网格划分图Figure 3 Grid division diagram of walking wheel

2.2 施加约束和载荷

行走轮工作时，围绕承载索垂直方向转动，因此，设置约束时，释放X轴方向的转动，其余方向的移动与转动均固定。

跑车工作时，跑车与重物总载荷全部作用在行走轮轴上，行走轮轴再作用于行走轮。设行走轮轴施加的压力均匀作用于轮孔上。6 个行走轮受总载荷为7 800 N，则作用于中心孔的均布压力Gn：

式(7)中：P′为单个行走轮中心孔压力(N)；D为行走轮中心孔直径，为50 mm；h为行走轮轮宽，为60 mm。

2.3 求解

跑车行走轮在施加约束和载荷后，经求解运算得到行走轮等效应力最小值为3.121×10-3MPa，最大值为11.84 MPa；等效位移最小值为0 m，最大值为1.778×10-4m。等效应力和等效位移云图如图4A 和图4B。

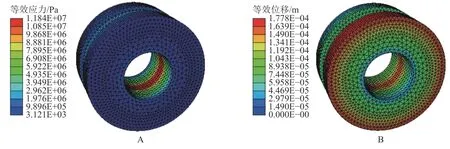
图4 等效应力云图(A)和等效位移云图(B)Figure 4 Equivalent stress nephogram and equivalent displacement nephogram

由图4A 可知：行走轮的最大应力出现在轮中心孔圈中间处，为11.84 MPa；最小应力出现在行走轮轮缘最外侧，行走轮压力沿2 侧轮缘变化平稳。由图4B 知：行走轮的最大位移发生在外侧车轮轮缘和轮中心孔圈中间处，变形量为1.778×10-4m。由于灰铸铁HT250 的许用应力为250.00 MPa，远大于工作时所受的最大应力，且行走轮最大位移量对其工作状态影响极小，因此强度和刚度均满足设计要求。

3 运输跑车-承载索耦合振动仿真分析

3.1 承载索模型简化

本设计中承载索钢丝绳是由6 绳股捻绕而成，具有一定的挠度。进行动力学分析时，需先把钢丝绳简化。在应用ADAMS 研究耦合振动时，还需要对钢丝绳进行柔性化处理。此处选择利用ABAQUS 软件将简化后的钢丝绳模型进行网格划分，模态处理后保存为MNF 过渡文件格式[8]，再将文件导入ADAMS 软件中，获得钢丝绳的柔性体。

3.2 承载索垂直位移时间历程分析

将SolidWorks 建立的跑车和模态处理后的承载索三维模型导入ADAMS 2020 应用软件，在ADAMS 中给跑车-承载索平移驱动motion 设置step 函数控制其运行速度[9]，当跑车速度为2 m·s-1时，step 函数为step(time, 0, 0, 2, 2)+step(time, 250, 0, 252, -2)，即前2 s 跑车速度由0 m·s-1加速到2 m·s-1，2～250 s 以2 m·s-1保持匀速运动，接近承载索端点时，由2 m·s-1减速到0 m·s-1。承载索钢丝绳长度为500 m，取250 m 处钢丝绳为研究点，跑车速度设置2 和4 m·s-1，跑车总质量取200、400、600 kg，索道倾斜角为20°，通过ADAMS 运动仿真得到承载索的垂直位移时间历程如图5 所示。

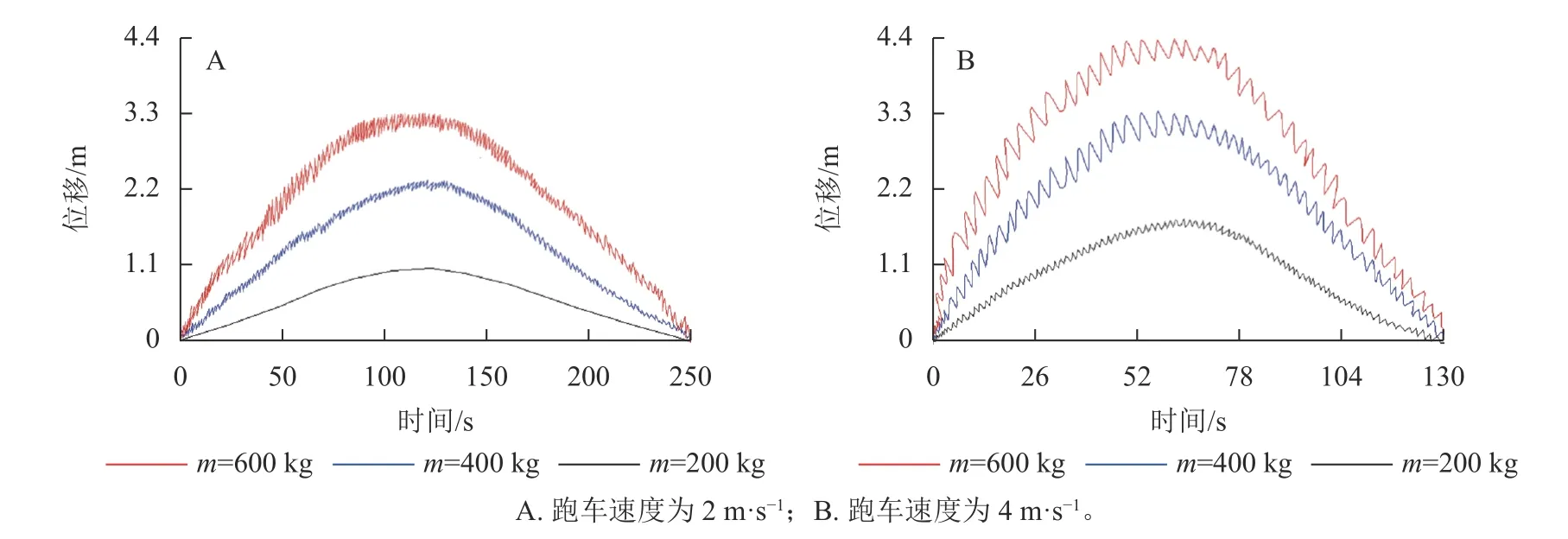
图5 不同跑车总质量下承载索的垂直位移时间历程Figure 5 Vertical displacement time history of the load-bearing cable under different total mass of sports cars

图5 可以看出：随着速度增加，跑车走完全程完成1 次竹材运输所需时间减少。承载索垂直位移随跑车速度的增加而增大，且通过图5A 与图5B 对比发现：速度为2.0 m·s-1时位移变化比4.0 m·s-1时密集，此时跑车在承载索上运行时对承载索施加的载荷频率变化快。当速度为4.0 m·s-1时，虽位移变化频率比2.0 m·s-1时小很多，但此时振幅剧增，位移最大可达4.39 m，容易导致跑车运输的货物掉落或承载索因挠度过大发生断裂。跑车运输工作过程中应尽量避免在此工况下工作。速度一定时，对比跑车在不同载荷下索道垂直位移变化发现，随着跑车载荷的增加，承载索垂直位移越大。载荷一定时，随着跑车速度增加，位移急剧增大。因此，载运量越大，速度越快，往返运输竹子时间越短，效率越高，但此时跑车与承载索的位移大，可能导致跑车运输货物掉落或索道断裂风险，安全性较低。为保证跑车运输竹材安全性和高效率，需要确定跑车优化运输条件。

4 基于ADAMS 的跑车运输仿真试验

跑车运输竹材的仿真分析结果表明：影响竹材运输效率和安全性的主要因素为运输速度和运输质量。此外，索道的倾斜角对运输安全性也具有较大影响[10]，但因索道运输时索道倾斜角条件主要取决于竹林场实际山体高度，通过增大或减小山顶与山底塔架的高度对倾斜角的影响不大。若要将塔架增减到影响倾斜角的高度，将增加安装运输成本，且随着索道支撑塔架的增高，运输安全性将受到极大影响。因此，竹材索道集材跑车运输系统主要应用于倾斜角为20°±4°的竹林地环境。综合考虑实际作业过程中运输速度、跑车与竹材总质量和索道倾斜角的变化对整个运输系统效率和安全性的影响，基于第3 节中ADAMS 构建的索道跑车运输仿真模型，开展Box-Behnken 仿真试验以确定优化参数组合[11]。

4.1 试验因素与评价指标

以运输速度(x1)、跑车与竹材总质量(x2)、索道倾斜角(x3)为试验因素，以索道最大位移(y1)和运输效率(y2)为评价指标进行仿真试验，因素水平编码如表3 所示。因试验存在2 个评价指标，且2 个指标之间存在一定的矛盾，即安全性越高，y1应尽可能小；而运输效率越高，则y2要偏大。此处采用多指标问题处理的综合评分法中排队评分法，对2 个试验指标进行综合评分(表4)，将多指标综合为单指标进行分析[12]。

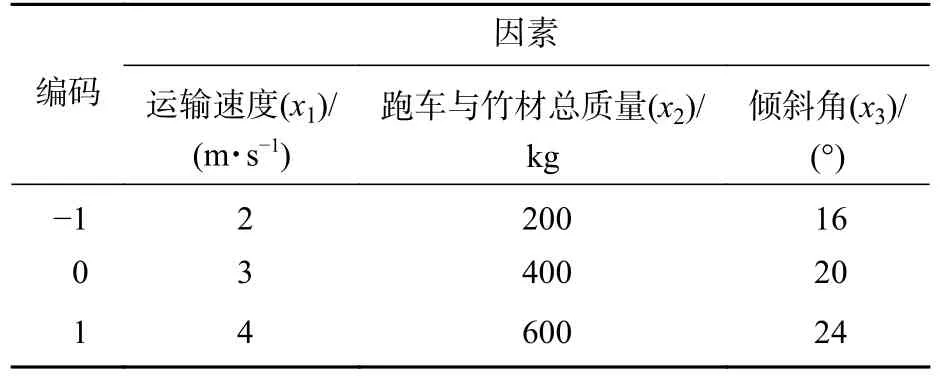
表3 试验因素编码Table 3 Test factor coding

表4 试验结果Table 4 Test result

式(8)中：t为运输总时间(s)。

根据仿真试验结果，对于最大位移指标，第8 号试验为0.98 m，位移量最小，赋予10 分；第7 号试验为4.39 m，位移量最大，赋予1 分。对于效率指标，第7 号试验为4.65 kg·s-1，效率最高，赋予10 分；第8 号试验为0.79 kg·s-1，效率最低，赋予1 分。对其他试验号各指标值的得分，根据其与该指标优秀值的差异按比例打分，最后对每号试验各指标的分数相加即得综合评分。

4.2 试验结果与分析

仿真试验结果如表4 所示。采用Design-Expert 13 对表4 数据进行回归分析[13]，得到评价跑车运输安全性与运输效率的综合评分指标(y3)关于运输速度(x1)、跑车与竹材总质量(x2)和索道倾斜角(x3)二次回归模型为：。回归方程的方差分析如表5 所示。回归方程模型显著性检验F1=25.15，P＜0.001 0，表明回归方程极为显著，与试验值拟合程度好，模型合理。模型的失拟性检验F2=2.82，P=0.170 8＞0.05，说明回归方程与实际误差所占比例很小，即试验误差小。由方差分析结果可看出：各因素对跑车运输安全性与运输效率综合影响由大到小依次为索道倾斜角、运输速度、跑车与竹材总质量。

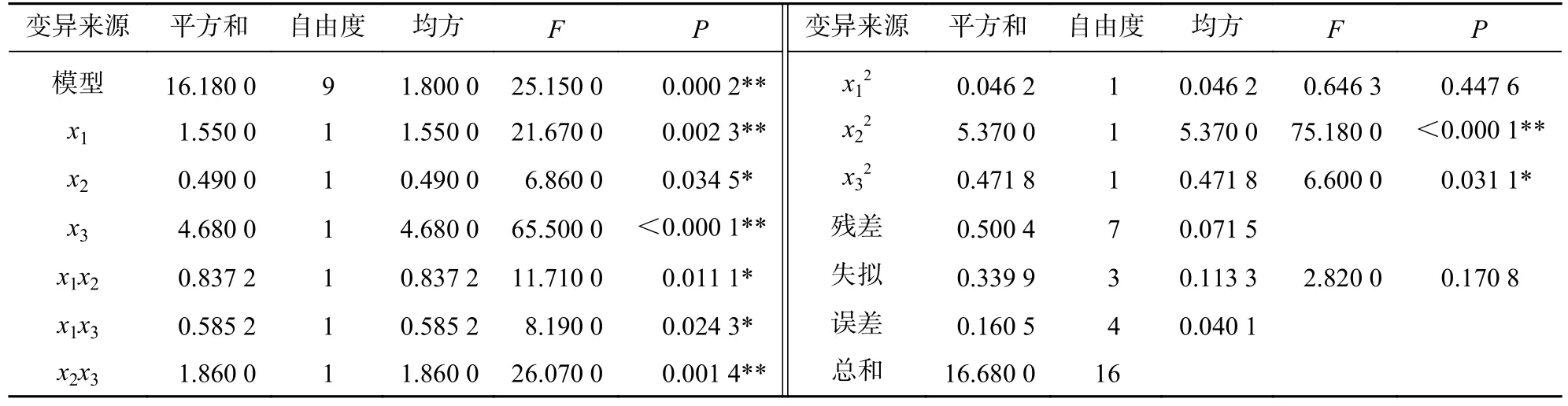
表5 综合评分指标(y3)方差分析Table 5 Analysis of variance of comprehensive evaluation index (y3)

4.3 响应面分析

为探究各因素的交互 作用，利用Design-Expert 13 建立运输速度、跑车与竹材总质量及索道倾斜角的交互因素对综合评分指标(y3)的响应面曲线，结果如图6 所示。由图6A 可知：运输速度一定时，随着跑车与竹材总质量增大，y3先减小后增大，最佳运输总质量为400～600 kg；总质量一定时，y3与运输速度呈正相关，最佳运输速度为3.0～4.0 m·s-1，运输速度和跑车与竹材总质量的交互作用显著。由图6B 可知：运输速度一定时，y3与倾斜角呈负相关，随着倾斜角的增大而减小，最佳倾斜角为16.4°～20.8°；倾斜角一定时，y3与运输速度呈正相关，随运输速度的增大而增大，最佳运行速度为2.8～4.0 m·s-1，跑车运输速度与倾斜角的交互作用不显著。由图6C 可知，倾斜角一定时，随着跑车与竹材总质量增大，y3先减小后增大，最佳运输总质量为420～580 kg；总质量一定时，y3与倾斜角呈负相关，随倾斜角的增大而减小，最佳倾斜角度为16.5°～20.4°，跑车与竹材总质量和倾斜角的交互作用显著。综合各交互因素响应曲面分析可得：当索道倾斜角为16.5°～20.4°、运输速度为3.0～4.0 m·s-1、跑车与竹材总质量为420～580 kg 时，综合考虑的跑车运输安全性和运输效率效果较好。

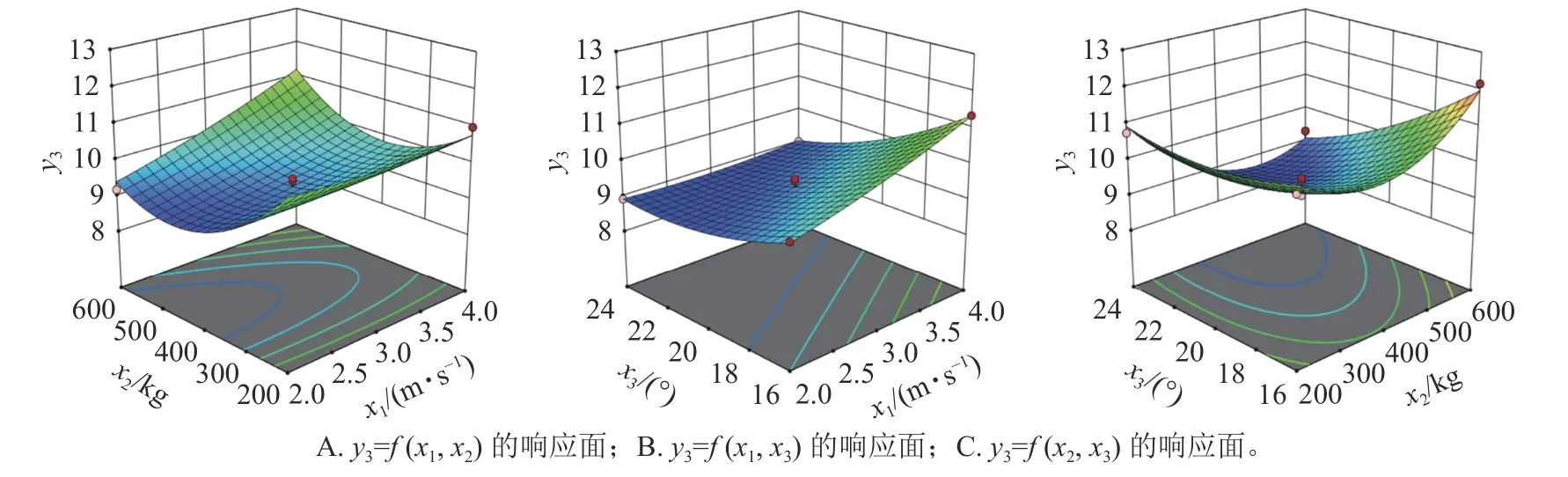
图6 交互作用对综合评分指标(y3)的影响Figure 6 Influence of interaction on comprehensive evaluation index (y3)

4.4 参数优化

为明确在跑车运输安全性和运输效率综合达到最优情况下的最佳参数组合，以y3值最大为优化目标，采用Design-Expert 13 中的优化模块对3 种因素在约束条件下进行求解，优化约束条件为：

求解得最佳参数组合：运输速度为3.95 m·s-1，跑车与竹材总质量为576.67 kg，索道倾斜角为17.09°，此时y3为12.31，达到最大，跑车运输安全性和运输效率综合达到最佳。

5 结论

针对山地竹材砍伐后运输下山困难，成本高，现行简易索式、轨道式等机械设备多由木材索式、轨道式改造而来，效果不稳定，实用性不高，安全得不到保障等问题，提出了一种专用于山地竹材运输的索道集材自充电跑车运输系统。通过实地调研，确定了竹材索道集材跑车运输系统基本设计参数，对悬索及跑车整体尺寸、功能进行设计，并对跑车关键受力部件进行强度和刚度校核。经有限元静力学分析可知：运输过程中跑车行走轮所受最大应力为11.84 MPa，远小于行走轮许用应力，最大变形量为1.778×10-4m，对跑车正常工作影响极小，强度和刚度均满足设计要求。使用ABAQUS 和ADAMS 软件对跑车与索道组成的系统进行了振动耦合分析，探究了运输速度、跑车与竹材总质量对运输安全性和效率的影响。当跑车速度越快，吊运竹材质量越大时，效率越高，但此时安全性急剧下降，最大位移量可达4.39 m，易发生安全事故。

承载索倾斜角为16.5°～20.4°、运输速度为3.0～4.0 m·s-1、跑车与竹材总质量为420～580 kg 时，跑车运输安全性和运输效率均较好；运输速度为3.95 m·s-1、跑车与竹材总质量为576.67 kg、索道倾斜角为17.09°时，运输安全性和效率综合达到最佳。