直驱风电场送出线路的正序电压极化距离保护适用性分析

李 斌，周博昊，何佳伟，戴 魏，王朝明，谢仲润

（1.智能电网教育部重点实验室（天津大学），天津市 300072；2.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省南京市 211106）

0 引言

加速推动新能源发电替代传统化石能源发电，构建以新能源为主力电源的新型电力系统是中国电力系统发展的重要趋势。与传统化石能源发电相比，新能源电源出力具有显著的波动性和随机性［1-2］，需要依赖大量的无功补偿装置、储能装置进行有效平抑。新能源电源、无功补偿装置、储能等设备的大量接入，导致新型电力系统的电力电子化特征愈发显著，故障响应过程的非线性与不确定性显著增强［3］，基于同步机特性设计的继电保护面临严峻挑战。

大规模风电通常经110 kV、220 kV 或330 kV联络线接入系统，目前送出线路的主保护一般为纵联保护。线路分布电容电流是制约现有纵联差动保护性能的主要因素，而故障暂态期间，风电接入系统存在的大量谐波会加剧电容电流对纵联差动保护的影响［4］。为此，国内外专家学者提出了多种补偿方法，包括相量补偿法［5］、时域电流补偿法［6］。相量补偿法只能补偿区外故障时的稳态电容电流，故障暂态期间补偿效果差；时域电流补偿法的效果与线路模型有关，可以消除电容电流的影响，但该方法对采样率要求高且计算量大。距离保护目前一般作为并网线路的后备保护，其动作性能对并网系统的安全运行至关重要。双馈风电场并网系统中，撬棒电阻的投入会增大风电场的正、负序阻抗［7］，加剧机组的弱馈特征，导致部分阻抗继电器的计算精度降低，还会在定子侧产生衰减的转速频率分量电流（一般在35～65 Hz 之间），引发频偏现象，对基于工频傅里叶算法的传统工频距离保护造成极大影响［8］。同时，受转子侧变流器矢量控制的影响，双馈型风机短路电流中会出现二次谐波，进一步加剧频偏特征［9］，干扰工频距离保护的正确动作。直驱风机的高谐波特性会造成工频相量计算出现误差［10］，并对工频距离保护产生影响。文献［11］考虑典型控制策略和穿越标准，仿真测试了逆变型新能源场站送出线路工频距离保护的动作性能，但其理论基础仍需研究。

目前，风电并网线路距离保护适用性的研究主要针对双馈风电系统，且现有文献大多集中讨论常规距离保护（如以母线电压为极化电压的距离保护）的动作性能，缺乏针对实际工程应用的广泛的正序电压极化式距离保护的适用性分析结果。目前，鲜有文献讨论风机不同穿越方式、不同稳态系统运行工况对正序电压极化式距离保护的适用性机理。因此，本文分析了永磁直驱风机输出电压、电流的暂态正负序分量幅相特征，对比了常规电源接入下保护工作原理，研究了永磁直驱风机送出线路采用基于正序电压极化的阻抗继电器的动作特性，定量分析了不同穿越控制方式、不同系统运行工况下比相结果出现的偏移程度。最后，在实时数字仿真系统（RTDS）中，基于国家电网有限公司某风电场搭建了典型直驱风机并网系统模型并进行测试，验证了适用性分析的结论。

1 永磁直驱风机的故障特征分析

典型的直驱风力发电系统的拓扑结构如附录A图A1 所示［12］。为更好地消除不对称故障下内环电流中的2 倍频分量，逆变型电源往往会配置负序电流抑制控制［13］。当并网点电压正序分量降低至80%以下时，直驱风机暂态期间应能主动提供动态无功电流，且其q轴电流增量ΔIq应满足［14］：

式中：UPCC为风电场并网点电压标幺值；K1为风电场 动 态 无 功 比 例 系 数，且1.5 ≤K1≤3.0；IN为 风 电场额定电流。

当直驱风机进入低压穿越控制模式时，外环比例-积分（PI）会迅速饱和，电流内环接管逆变器控制并快速响应指令值变化。在故障稳态阶段，当公共连接点（PCC）处电压跌落至UPCC时，并网逆变器无功电流指令值iqref表示为［15］：

式中：Iq0为稳态q轴电流。若采用最大容量限制有功功率的穿越方式，则有功功率电流指令值idref如式（3）所示。

式中：imax为逆变器最大允许电流。

当送出线路发生相间故障时，直驱风电场送出线路保护安装处的A、B、C 相电压Uma、Umb、Umc和电流Ima、Imb、Imc的信号如图1（a）所示。电压、电流中的正序、负序分量如图1（b）和（c）所示。由图1 可得，稳态时并网逆变器的有功电流控制为1.0 p.u.，无功电流控制为0，故对外表征为全发有功功率，电压、电流波形相位相同，正序电压、电流分量相位相同。送出线路相间短路故障下，内环电流会在20 ms左右快速达到故障稳态阶段。由于负序电流抑制与穿越控制策略的影响，在故障稳态时，正序电流相对正序电压出现了近30°的相位偏移。

2 直驱风电场送出线路中以正序电压作为极化电压的阻抗继电器适用性

本章将介绍正序电压极化式距离保护的设计原理；对比常规电源、新能源接入下比相结果的推导过程，剖析风电接入下该保护可靠性下降的机理；通过引入功率因数角的指标，量化分析不同穿越方式、不同系统运行工况的适用情况。

2.1 常规电源接入下阻抗继电器的工作原理

以正序电压作为极化电压的阻抗继电器的动作方程可表示为［16］：

以正向BC 两相短路故障为例，不妨假设短路故障前系统空载，则BC 相间阻抗继电器的补偿电压为：

式中：Zm为测量阻抗；Zset为整定阻抗，一般取80%～85%的 线 路 阻 抗；为B、C 相 间 线 电 流；为B 相电流。

保护安装处的极化正序电压等于背侧电源内电势减去正序电流分量在保护背侧正序阻抗上的压降，即

该故障情况下的继电器动作方程可表示为：

正向故障下，其动作特性是以Zset与-0.5ZS两点连线为直径的圆，上述动作特性如附录A 图A2所示。即使发生正向出口处金属性短路故障，故障相间电压为0，但正序极化电压并不为0，图A2 所示基于正序极化电压的阻抗继电器的阻抗动作圆包含坐标原点，因此能极大缓解常规Ⅰ类阻抗继电器的死区问题。

2.2 直驱风机故障穿越控制对阻抗继电器的影响

2.2.1 影响机理分析

对于跟网型永磁直驱风机，在低压穿越的故障稳态阶段，正序网络可等效为压控电流源，由于存在负序电流抑制控制，负序阻抗无穷大可等效为开路，此时线路区内故障的复合序网如图2 所示。图中：母线M、N内为正向保护区间；ZL为线路全长正/负序阻抗；k为归一化的故障距离，且0 ＜k＜1；kZL为故障点到M侧保护安装处线路的正/负序阻抗；(1-k)ZL为故障点到N侧母线间线路的正/负序阻抗；ZSN1和ZSN2为N侧电源的正、负序系统阻抗；I为永磁直驱风机正序电流幅值；IM1为M侧保护安装处的正序电流；γ为功率因数角；θPLL为锁相环提供的并网点电压相角，忽略锁相环动态跟踪性能引起的误差，可近似认为θPLL与相位相同，其中，为M侧保护安装处测得的正序电压。

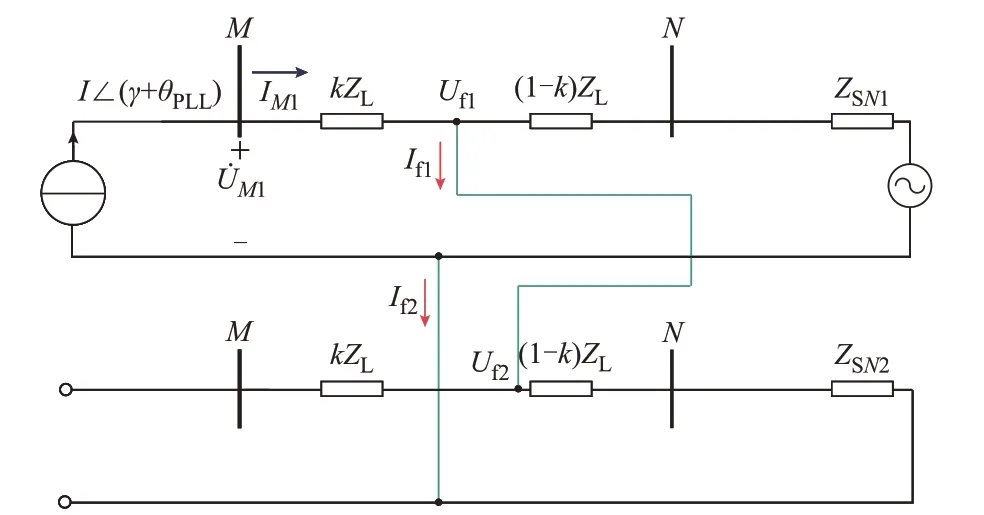
图2 正向区内相间故障复合序网络Fig.2 Complex sequential networks with phase-to-phase fault in positive area

由图2 可知，对于相间金属性短路故障，故障点处的正、负序电流相量幅值If1、If2相等，相位相差180°；故障点处的正、负序电压相量的幅值Uf1、Uf2相等，相位相同。同时，由于正序电流在正序线路阻抗上的压降作用，M侧保护安装处的正序电压UM1大于故障点处的正序电压Uf1。但由于风机并网换流器的负序抑制作用，负序电流约等于0，M侧保护安装处的负序电压等于故障点处的负序电压Uf2。以BC 相间短路故障为例，极化电压可表示为：

补偿电压可表示为：

式中：t为时间；Ud+、Uq+和Id+、Iq+分别为正序电压和正序电流在dq同步旋转坐标系下d、q轴的投影；ωu为实际dq同步旋转坐标系的旋转角速度；ωPLL为锁相环输出的dq同步旋转坐标系旋转角速度，在忽略锁相环跟踪性能影响时可认为二者相等。

并网逆变器往往采用电网电压定向控制的方式，即网侧逆变器dq同步旋转坐标系下的数学模型中往往将电压定位在d轴上，即Ud+=Ug（Ug为相电压幅值），Uq+=0。

将式（11）代入式（10），则相间阻抗继电器的动作方程Fop可表示为：

本文将正序电压相量超前正序电流相量的角度称为功率因数角γ，即

将式（13）代入式（12），在配置负序电流抑制控制情况下，相间短路故障下直驱风机送出线路的相间阻抗继电器动作方程变为：

根据图2 可得相间继电器的测量阻抗Zm为：

保护安装处正、负序电压和电流有：

负序电流被抑制至0，将式（16）代入式（15）有：

根据图2 可知，此时保护安装处测量得到的负序电压等于故障点处的负序电压，同时根据故障边界条件，式（17）可改写为：

根据式（15）—式（18），不考虑过渡电阻影响的情况下，直驱风机送出线路上相间阻抗继电器的测量阻抗仍然可以准确反映故障位置。对比式（7）与式（14）可知，常规电源在电磁暂态时间尺度下，发电机转速不变，ZS不变，此时保护的动作方程主要由测量阻抗Zm决定，而测量阻抗Zm可以准确反映故障位置，因此，以正序电压作为极化电压的阻抗继电器可靠性较高。但当其应用于直驱风机送出线路时，由于送出线路故障时并网逆变器具备快速响应的双环控制，且配置穿越控制及负序电流抑制控制，其故障后低压穿越期间输出的有功、无功功率会迅速发生变化，此时相间阻抗继电器的动作方程由测量阻抗和功率因数角共同决定。虽然此时测量阻抗仍然准确反映故障距离，但不同穿越控制策略下的功率因数角存在差异，会影响相间阻抗继电器的可靠性，需要详细分析。在接地故障下存在较大幅值且相位不受控制策略影响的零序电流分量，在零序电流补偿项的相位钳位下，保护可靠性仍相对较高，其理论推导与仿真测试详见附录B。

2.2.2 不同低压穿越策略下阻抗继电器的可靠性

不同国家的并网导则如附录C 图C1 所示。可以看出，虽然在指标上各国标准略有差异，但设计上均采取了增发无功方式实现低压穿越［17-22］。根据文献［14］，低压穿越期间的无功电流指令值下限可由式（2）计算获得，后续将分为有功置零、定有功功率与限有功功率3 种典型低压穿越控制方式对相间阻抗继电器适用性进行分析。控制参数不准确对比相结果影响较小，故无须考虑该因素（详见附录D）。

正序电压极化式距离保护需要使用傅里叶算法获取故障后电压、电流的幅值、相位，并在保护多次进入动作区间后，输出比相结果并出口动作，此时逆变器已处于故障稳态阶段。对于“增发无功、有功置零”的低压穿越方式，低压穿越期间直驱风机增发无功功率，不发有功功率，此时功率因数角为：

对于“增发无功、定有功”的低压穿越方式，低压穿越期间直驱风机增发无功功率，有功功率维持稳态水平，低压穿越期间逆变器正序d轴电流id+可表示为：

式中：id0+为稳态时正序d轴电流。此时，功率因数角如式（21）所示。

式中：iq0+为稳态时正序q轴电流。

对于“增发无功、限有功”的低压穿越方式，低压穿越期间按最大容量原则限制有功电流（如式（3）所示），此时功率因数角为：

根据式（19）、式（21）、式（22）可知，功率因数角与穿越策略、系统稳态工况等相关，可以使用归一化功率因数角γn定量评估保护的适用性：

γn等于0 表示保护适用性最好，几乎不受影响，γn越大则说明保护适用性越差。不同穿越控制方式、不同稳态工况条件下，以正序电压为极化电压的比相式距离保护动作情况如图3 所示。图中：idx、iqx、γx分别为比相结果x下的d、q轴电流分量及功率因数角，其中,x=1,2。零有功、定有功、限有功分别表示“增发无功、有功置零”“增发无功、定有功”“增发无功、限有功”的低压穿越方式。

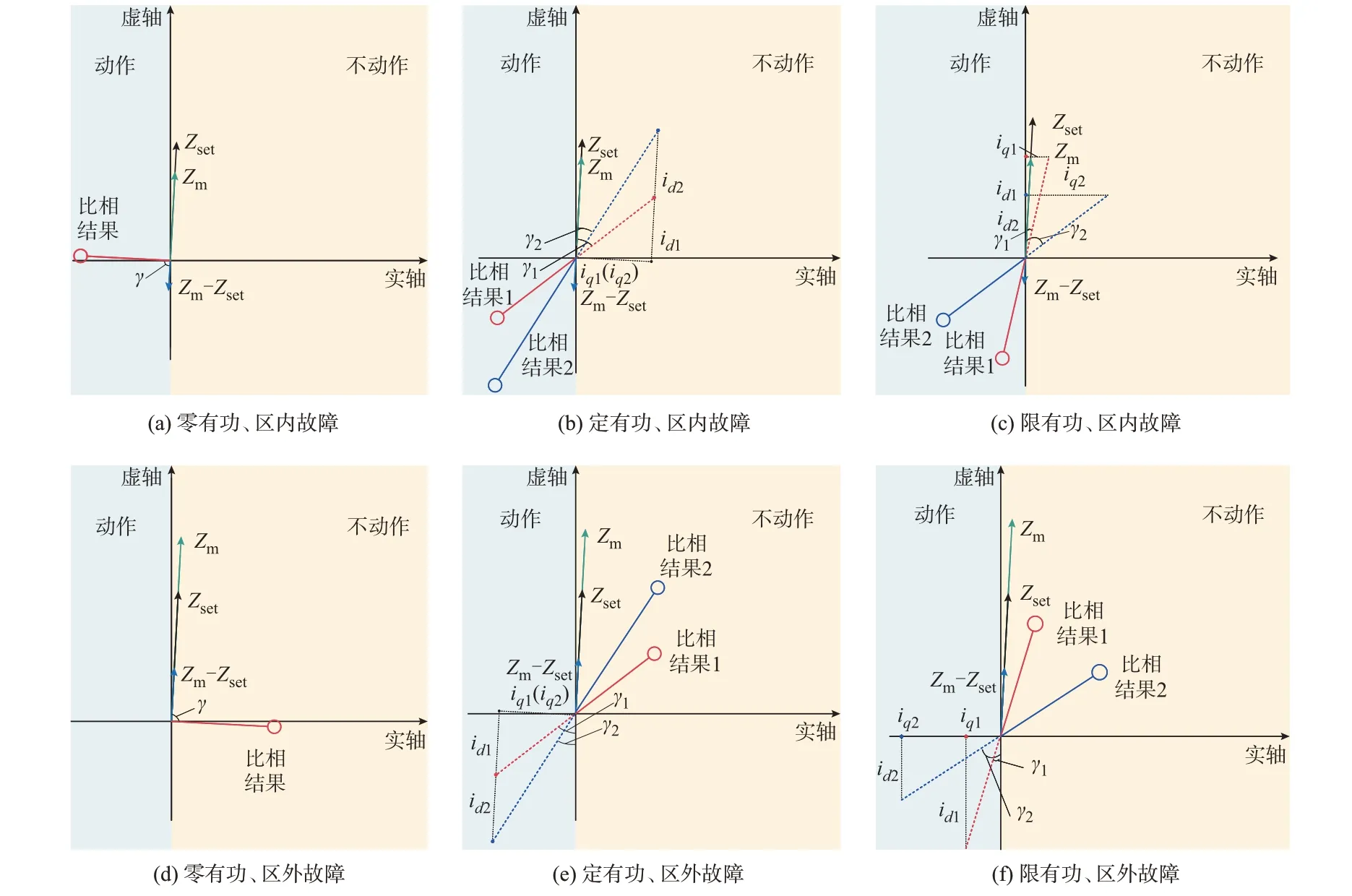
图3 不同穿越控制策略、不同工况对相间阻抗继电器的性能影响Fig.3 Influence of different ride-through control strategies and different operation conditions on performance of phase-to-phase impedance relay

根据图3 可知：1）“有功置零”的低压穿越方式下阻抗继电器的可靠性几乎不受影响，区内外故障下均处于最可靠工作状态；2）“定有功”的低压穿越方式下，阻抗继电器的可靠性会下降，且可靠性与系统稳态工况有关，直驱风电场稳态时有功功率出力越大，“增发无功、定有功”穿越方式下阻抗继电器的可靠性越低；3）“增发无功、限有功”的低压穿越方式下，阻抗继电器的可靠性会下降，受最大允许电流imax的钳位效果，当故障较严重并导致并网点电压跌落较多时，增发无功功率较小，相间阻抗继电器的可靠性相对较高。

3 RTDS 实验测试

3.1 系统参数

为测试直驱风电场的送出线路距离保护适用性，参考国家电网有限公司某实际风电场的拓扑与系统参数，根据文献［23］采用单机等效方式，在RTDS 平台搭建了如附录A 图A1 所示的典型直驱风电场并网系统模型。其中，50 台2 MW 的直驱风机经过箱式变压器（0.69 kV/35 kV）通过汇集线路送至风电场主变压器（35 kV/220 kV），升压后经60 km 送出线路将额定有功功率100 MW 的电能传输至主网内。主要参数如下：系统侧电源正序阻抗为3.14 Ω，零序阻抗为8.314 Ω；风电场主变压器（YNd11）容量为200 MV·A；短路阻抗为10.36%；220 kV 送出线路的正序阻抗为（0.013 326+j0.266 079)Ω/km（正序阻抗角约为87.8°），零序阻抗为（0.030 791 5+j0.814 968)Ω/km；箱 式 变 压 器（Dyn11）额定容量为2 MV·A；短路阻抗为7%；额定风速为10 m/s；风电场动态无功比例系数为1.5；直驱风机低压穿越方式为增发无功功率、最大容量限制有功功率；逆变器最大耐受电流为1.4 p.u.。

3.2 正序电压作为极化电压的阻抗继电器性能测试

整定系数取0.8，故障发生于2.0 s，持续300 ms，区内故障点F1为线路中点，区外故障点F2为线路末端，区内相间故障的测试结果如图4 所示，区外相间故障的测试结果如图5 所示。图中：Id和Iq分别为内环d、q轴电流的测量值。

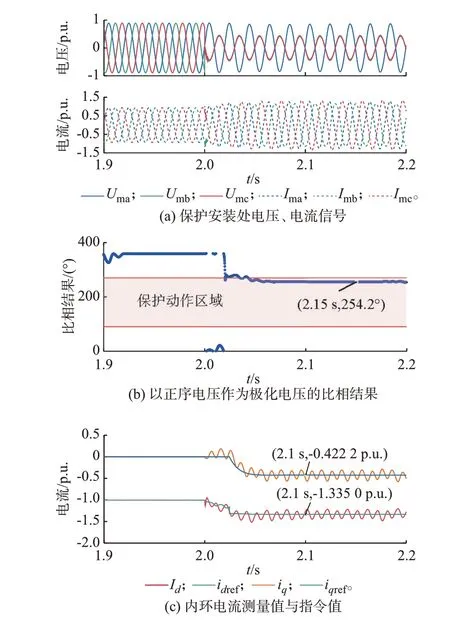
图4 区内故障测试结果Fig.4 Test results with internal faults

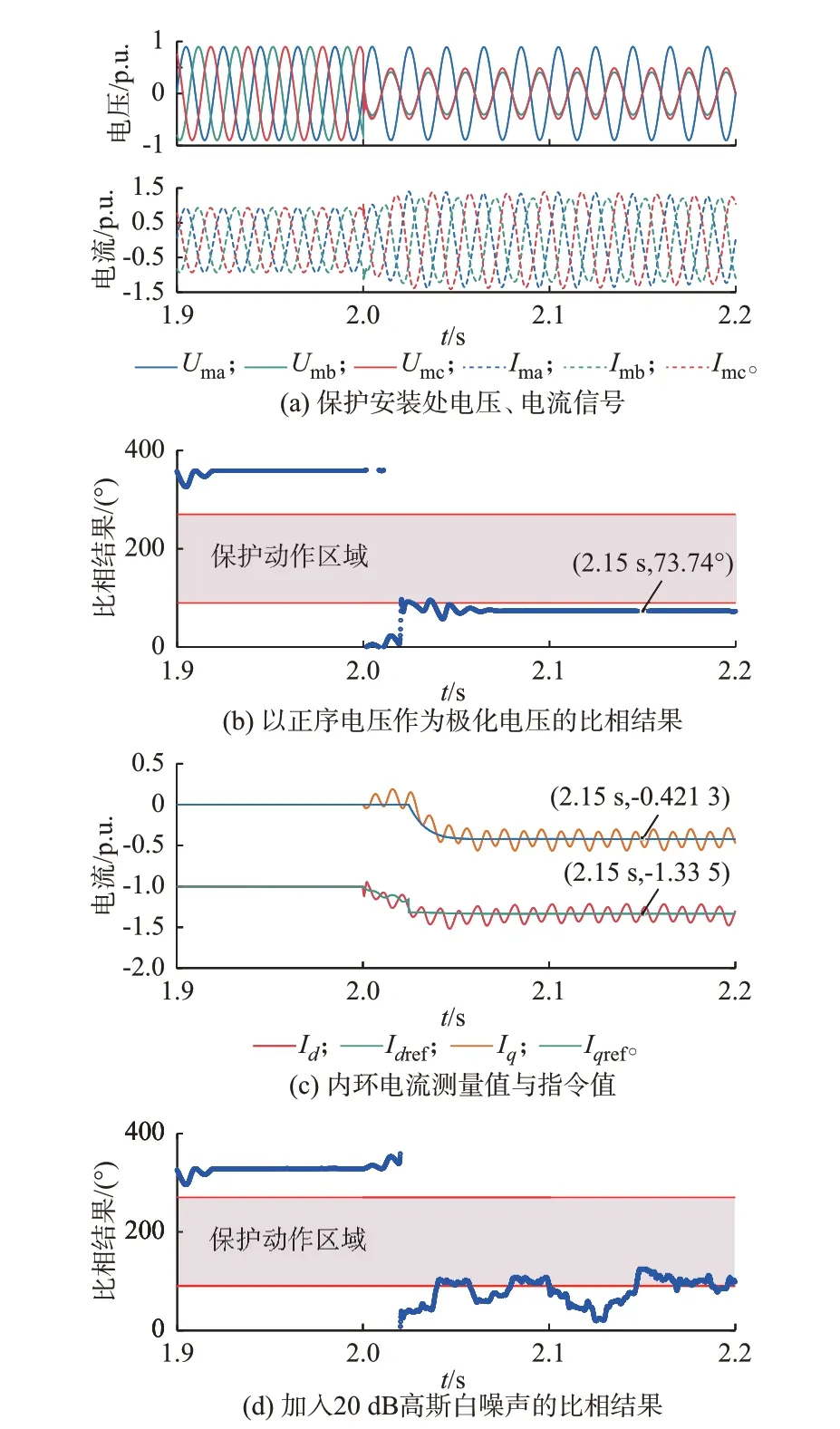
图5 区外故障测试结果Fig.5 Test results with external faults

3.2.1 区内故障测试结果

如图4（b）所示，区内相间故障时，正序电压极化的相间阻抗继电器的比相结果约为254.2°，十分接近动作边界，可靠性较差。

由图4（c）所示内环电流测量值与指令值可知，根据式（22）计算得到的功率因数角γ为-17.579 8°，正序电压极化的阻抗继电器比相结果计算值为250.250 2°，与实际结果近似相等，误差为1.55%，这说明区内故障的适用性分析理论正确。

3.2.2 区外故障测试结果

如图5（b）所示，区外相间故障时，正序电压的相间阻抗继电器的比相结果约为73.74°，十分接近动作边界，可靠性较差。当加入信噪比为20 dB 的高斯白噪声后，如图5（d）所示，比相结果会进入动作区间内，易造成误动现象。

由图5（c）所示内环电流测量值与指令值可知，式（22）中功率因数角γ约为-17.514 7°，正序电压极化的阻抗继电器比相结果计算值为70.285 3°，与实际结果近似相等，误差为4.68%，这说明区外故障的适用性分析理论正确。

归一化功率因数角在区内相间故障时为0.804 7，在区外相间故障时为0.805 4，同时区内、区外相间短路故障下，相间继电器的比相结果均接近动作边界，保护的可靠性大大降低，验证了所提归一化指标的有效性。

3.3 不同穿越策略下阻抗继电器性能测试

由2.2.2 节分析可知，不同穿越控制方式下，正序电压极化距离保护适用性存在差异，为验证理论分析的正确性，本节选用如下3 种穿越方式进行正向金属性故障测试。

穿越方式Ⅰ：增发无功、最大容量限制有功（imax=1.4 p.u.）。

穿越方式Ⅱ：增发无功、有功置零。

穿越方式Ⅲ：增发无功、定有功（工况1 为稳态d轴电流id0=0.5 p.u.，工况2 为id0=1.0 p.u.）。

整定系数取0.8，不同故障类型下阻抗继电器的动作情况如表1 所示。

表1 不同穿越策略下的保护动作情况Table 1 Protection operation conditions with different ride-through strategies

由表1 可得出以下结论：

1）不同穿越控制策略下，保护的适用性存在差异。相比穿越方式Ⅰ、Ⅲ，穿越方式Ⅱ的归一化偏移角指标在区内、外故障下均保持较低水平，说明穿越方式Ⅱ下保护的可靠性最高。

2）当采用穿越方式Ⅰ、Ⅲ时，相间短路故障下归一化偏移角指标显著增加。此时，保护的可靠性迅速降低。

3）对于穿越方式Ⅲ，工况1 的区内、外相间短路故障下γn分别为0.605 6、0.598 0，工况2 的区内、外相间短路故障下γn分别为0.800 0、0.844 9，显然工况2 保护的可靠性更低，说明随着风电场稳态出力的增多，定有功控制下保护的可靠性会降低。

4）对于穿越方式Ⅰ，F1点相间短路故障时，PCC 电压有效值约为0.736 45 p.u.；F2点相间短路故障时，PCC 电压有效值约为0.757 50 p.u.。上述两种故障情况下归一化指标分别为0.824 4、0.818 9，验证了“增发无功、最大容量限制有功”低压穿越策略下，当并网点电压跌落较少时，阻抗继电器的可靠性更低。

上述测试结果与理论分析吻合，显然，直驱风机送出线路正序电压极化距离保护与穿越方式Ⅱ的直驱风电场最为适配。若直驱风电场采用穿越方式Ⅰ或Ⅲ，相间故障时阻抗继电器的可靠性会降低，特别是采用穿越方式Ⅲ时，风电场稳态时若处于大功率运行状态，相间继电器的可靠性会进一步降低。

4 结语

本文重点探讨了正序电压为极化电压的比相式距离保护在永磁直驱风电场并网线路上的动作性能，并分析了不同穿越控制策略及运行工况对动作性能的影响，得到结论如下：

1）受暂态穿越控制与负序电流抑制策略的影响，故障穿越期间直驱风机送出线路上的正序电流、电压相量间会出现与低压穿越控制策略、系统稳态工况有关的功率因数角，降低正序电压极化距离保护的可靠性，表现为区内相间故障易拒动、区外相间故障易误动。

2）不同穿越策略下，正序电压极化距离保护的可靠性有所不同：“增发无功、有功置零”的穿越方式下相间阻抗继电器的可靠性最高；“增发无功、定有功”与“增发无功、限有功”的穿越方式下相间继电器可靠性会显著降低。

3）“增发无功、定有功”的穿越方式下，稳态时风电场发出有功功率越大，低压穿越期间相间继电器的可靠性越低。

4）本文虽以直驱风机为例进行讨论，但所提出的适用性分析结论同样适用于光伏、储能电站、柔性直流系统的交流侧。本文忽略了负荷电流引起功角摆开的问题，同时以相间金属性故障为例进行分析，后续可针对功角、过渡电阻等问题进一步深入研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。