基于转子动能调节的风电输出功率平滑控制策略比较与改进

朱 瑛，王志聪，石 琦，卫志农

（河海大学能源与电气学院，江苏省南京市 211100）

0 引言

随着风电渗透率的提高和风机大型化的趋势日益显著，平抑风电输出功率波动成为研究热点。为了提高经济效益，风电机组一般运行于最大功率点跟踪（MPPT），然而，由于风速的随机波动，尤其是在湍流风速下，风电输出功率波动剧烈，给电网电压或频率带来扰动，进而威胁电网运行稳定性［1-3］。为了解决上述问题，有学者提出了多种平滑风电输出功率的方法，原理上基本可以分为两大类：间接功率控制［4-5］和直接功率控制［6-8］。

间接功率控制通过储能系统的充放电功率与风电波动功率对消，进而实现功率平滑［4］。储能系统包含电池、超级电容器、超导磁体、飞轮、混合储能装置等，主要被用于平抑大型/规模化风电并网系统长时间尺度的功率平滑，在实际应用中存在成本高昂等问题［8］。

对此，有学者将目光投向利用大型风电机组自身资源进行功率平滑，其中，基于风机惯性动能平抑风电机组输出功率波动的方法成为研究热点。文献［9］以经典控制理论为依据，采用传递函数方法推导了风能转换系统有功功率控制回路中的虚拟滤波器，通过调节存储在风轮旋转质量块中的动能进行输出功率平滑。在MPPT 控制框架的基础上，文献［10］探究了转速外环控制器参数对稳定性和功率平滑效果的影响，但系统输入未涉及湍流风况场景，亦未将频域与时域波动有效对应。文献［11］研究了斜线平滑策略，旨在实现平滑控制效果的同时有效降低变桨动作频率和幅度，但未对参数配置原理进行充分阐释，所呈现的平滑提升亦不明显。文献［12］分析了依据电网调度指令进行被动变速从而实现恒功率输出的方法，虽然最大程度平滑了输出功率，但此控制方式弃风严重，风能捕获效率大大降低，并且在湍流风速波动剧烈时存在失稳的风险。文献［13-14］提出了不同的转子动能控制架构，但均未阐明实际输出与有功参考值之间的关系；文献［15］提出了包含转子动能在内的协调平滑控制框架，并将有功参考值与实际输出进行明确区分，但实际输出并未有效跟踪功率指令。因此，当前基于转子动能平滑的控制架构和有功参考值选取方法仍需改进。

目前，基于转子动能控制设置输出平滑功率参考值的方法有下面几种。文献［14-15］均在MPPT方法的基础上采用滑动平均滤波算法。然而，目前对于时间窗长度在数值上的界定尚未有统一标准。文献［16］提出在风电控制系统中引入带通滤波器以滤除风电输出中的电网频率敏感分量，旨在平滑功率的同时维持高发电效率，但文中并未提及频率敏感分量的来源。文献［17］在MPPT 控制回路中引入一阶数字滤波器进行平滑，但通过时域波形和频谱分解结果可看出，此平滑方式仅在高频段生效，低频段反而使得功率波动放大。因此，整体上功率平抑效果并不显著。文献［18］开创性地提出使用二阶数字滤波器生成有功参考值指令，然而未阐述滤波器参数的配置原则。此外，文中未将稳定性问题纳入探讨范围。

综上所述，当前风电机组依托转子动能进行功率平滑的研究存在以下几个难点：1）如何权衡输出功率平滑效果与风电机组发电效率之间的矛盾；2）如何明确兼顾平滑目标和风电机组转子转速稳定的有功参考值选取方法。

针对上述问题，本文提出了一种基于变参数二阶滤波的转子动能控制方法，以平滑湍流风况下的风电机组输出功率。该方法具有如下优势：1）通过镇定手段保证风电机组低转速时的稳定性，有效避免了风速快速下降时的电磁功率跌落；2）控制环节中引入模糊推理子系统，依据湍流风况在线修正滤波器系数，提升了平抑功率波动效果。文中分别建立了基于所提控制策略的风电仿真模型及实验平台，通过仿真与实验验证了所提控制策略的有效性。

1 基于一阶滤波的转子动能控制的功率平滑方法

1.1 风力发电系统模型

本文以永磁直驱风力发电系统为基础，研究基于转子动能的功率平滑方法。典型永磁直驱风力发电系统结构如附录A 图A1 所示，系统由风机、永磁同步发电机（PMSG）、背靠背变换器与直流侧电容组成。PMSG 直接连接风机，风机将吸收的机械功率Pw传递给发电机，发电机发出电能Pe，通过背靠背变换器并入电网。

依据空气动力学原理，风轮捕获的机械功率为：

式中：ρ为空气密度；R为风机叶片半径；v为风速；Cp(λ，β)为风能利用系数［10］，是关于叶尖速比λ与桨距角β的非线性函数。

式中：ω为风电机组转子的机械角速度。

风电机组在额定风速以下时，为提高风能利用率，将桨距角β调节为0°，在风速变化时改变发电机转子转速，让λ维持在最佳叶尖速比λopt，可使得风能利用系数Cp恒定在最大值Cp，max［19］。此时，风机可以捕获的最大风功率Pmax为：

因此，以转速表征的风电机组最佳输出功率Popt可表示为：

式中：kopt为最佳功率比例系数，是仅与风电机组参数相关的常数。

风电系统传统基于功率信号反馈（power signal feedback，PSF）的MPPT 方法将风电机组有功参考值设置为Popt，通过闭环调节手段便能实现MPPT。

1.2 基于一阶滤波的转子动能功率平滑控制原理

一阶低通滤波器简单实用，在储能系统功率平滑的算法中广泛应用，已有研究也将一阶滤波（first order filtering，FOF）方法引入风电机组传统PSF 控制架构，旨在MPPT 的基础上增强功率平滑效果，其基本思路是在PSF 方法的参考功率上级联一阶低通滤波器。本文以PMSG 为例进行分析，其运动方程为：

式中：Tw为风机输出的机械力矩；Te为发电机的电磁转矩；J为包括风轮和发电机在内的系统转动惯量。

将式（5）改写成功率的表达式，有

式中：Pr为转子动能吸收或释放的缓冲功率。

将电磁功率Pe替换成平滑的参考功率，式（6）变为：

式中：Pref为期望发电机输出的平滑功率参考值。

将式（7）从t0到t1的时间段进行积分，可得：

式中：ωt0和ωt1分别为t0时刻和t1时刻的转速值。ωt1可由转速增量表示成ωt1=ωt0+Δωt，而Δωt即为积分时间间隔ΔT=t1-t0内的转速增量。

ωt1=ωt0+Δωt代入式（9）可得：

求解式（10），舍去恒负值根，可得Δωt为：

可得ωt1的表达式为：

根据式（12）可以得到基于转子动能控制的风电机组参考转速，发电机侧控制框图如图1 所示。图中：ω*为转速参考值，ω和ω*分别代表推导过程中的ωt0和ωt1；ids、iqs和、分别为两相旋转坐标系下d轴和q轴的实际电流与参考电流值；、分别为两相旋转坐标系下的d轴和q轴参考电压；、分别为两相静止坐标系下的α轴和β轴参考电压；Sa、Sb、Sc为换流器所需的开关函数信号；ia、ib、ic为发电机三相电流；θ为发电机转子电角度；SVPWM 表示空间矢量脉宽调制。两个延时模块用于同步转速信号，其延迟时间ΔT亦是积累动能的时间，系统惯量越大，转速变化越缓慢，需要更多的时间积攒动能。理论上，依据式（12），按照图1 的参考转速取值及传统转速闭环比例-积分（PI）控制器调节，在不触及转速运行上下限的情况下，PMSG的实际输出功率能准确跟踪有功参考值。

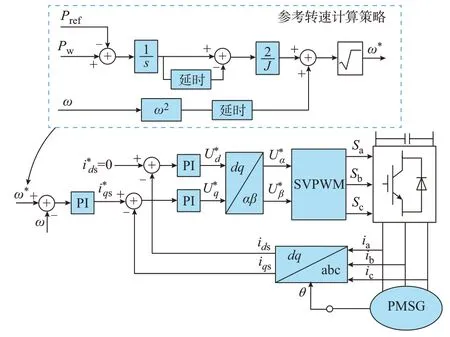
图1 基于转子动能的发电机侧控制框图Fig.1 Block diagram of generator-side control based on rotor kinetic energy

1.3 FOF 方法的局限性分析

由于一阶滤波器级联在功率反馈方法之后，滤波器的引入会改变发电机的输出特性，导致系统机械状态量即转速的变化，转速变化又会导致风电机组输出转矩变化，从而影响转速和发电机输出特性。下面从传递函数角度具体分析滤波器对系统的影响。引入该一阶滤波器后，输出功率参考值变更为：

式中：Pref1为引入一阶滤波器后输出功率的参考值；G1st为一阶滤波器传递函数表达式；τ为一阶滤波器时间常数，理论上，τ值越大，滤波效果越强。

采用小扰动分析法，在稳态运行点(v0，ω0)对机械功率和电磁功率进行泰勒展开，略去高次项后可得：

式中：Δ 项为线性化过程中变量的增量。

将式（14）代入式（6）的发电机运动方程并进行双边拉普拉斯变换可得：

Gω/v-1st(s)即为FOF 方法下风速到转速的无量纲传递函数。由式（15）可见，在转速闭环控制回路中引入滤波器对系统传递函数的影响并不是滤波器的简单级联，而是同时改变了系统的零点与极点。

以6 MW 永磁直驱风电机组为研究对象进行频域分析，机组参数见附录A 表A1。附录A 图A2（a）所示为Gω/v-1st(s)对应幅频特性随时间常数τ的变化情况。参考运行点取v0=8 m/s，ω0=0.864 rad/s的典型最佳功率点。可以观察到，随着τ值的增大，在低频段转速幅频特性逐渐产生超调。进一步，以图A2（a）为基础，画出Gω/v-1st(s)的Bode 图最大幅值Mw随时间常数τ的变化规律曲线，如图A2（b）所示。可见，随着τ值的增大，Gω/v-1st(s)的Bode 图在τ=0.2 附近出现超调，且超调量随τ单调递增。

根据文献［10，20］的理论分析，风电机组动态控制过程中转速稳定的充分条件为风速波动不产生对应转速超调。分别取τ=0.125 和τ=0.5 两种参数值代表转速未超调与超调的两种模态，和PSFMPPT 方法进行对比，其传递函数幅频特性如附录A 图A3 所示。由图A3（a）和（b）可知，一阶滤波器的引入会改变转速运行特性，具体表现为抑制高频转速波动，但弱化了低频段的波动的平滑能力，且τ的增大会进一步放大低频段的转速振荡。

同理，根据电磁功率与转速3 次方的一阶滤波关系，可推导出从风速到功率的无量纲传递函数为：

图2 所示为GP/v-1st(s)对应幅频特性随时间常数τ的变化情况。可见，τ值的增大能强化对高频功率波动的削弱效果；而无论转速是否产生超调，在低频段都会放大功率的波动幅值。实际上，往往是此类低频高幅值功率波动对电网产生较大冲击。因此，不能简单地按照一阶滤波器的截止频率设计滤波参数。由此可见，通过增大滤波时间常数τ期望达到更好平滑效果的做法仅适用于高频段波动，并不能抑制低频段的功率波动。

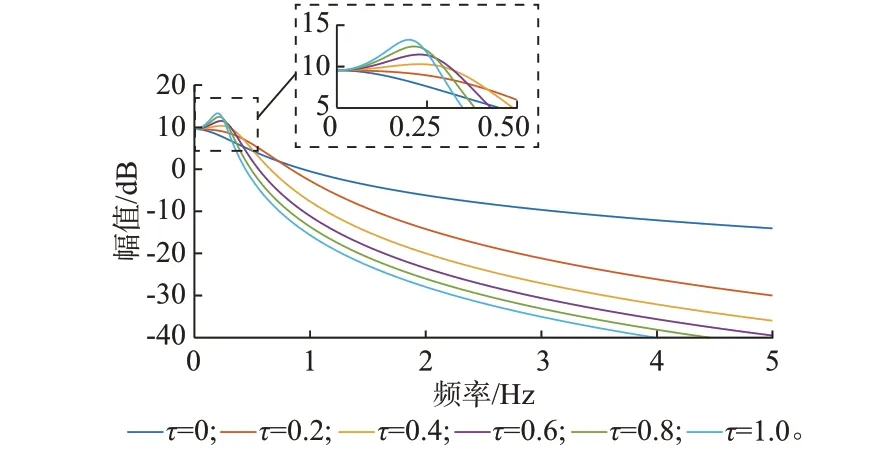
图2 GP/v-1st(s)幅频特性与时间常数τ 的关系Fig.2 Relationship between amplitude frequency characteristic of GP/v-1st(s) and time constant τ

根据上文分析，可总结出FOF 方法的局限性在于：一阶滤波器仅有一个可调参数τ，为提升平滑效果，仅能通过增大滤波时间常数τ实现，而τ值增大所带来的平滑效果提升主要体现在高频段，并不足以弥补被放大的低频转速振荡和功率振荡。因此，FOF 方法对输出功率的平滑作用仅限于高频段。

2 基于改进二阶滤波的转子动能功率平滑控制策略

考虑到FOF 方法的局限性，可考虑引入更高阶的滤波器以应对一阶滤波可调参数不足的状况。文献［18］虽率先提出将二阶滤波器引入功率平滑方法中，构成二阶滤波（second order filtering，SOF）方法。但未对滤波器参数配置方法提供充分有效的说明。此外，由于文中采用固定的滤波器参数，不能较好适应湍流风速波动大的特征，在风速下降时存在转速失稳的风险。因此，需要进一步研究滤波参数的选取原则，并提出基于风电机组实际工况在线修正参数的方案。

2.1 二阶滤波平滑的原理及取值原则

引入的二阶滤波器若为纯两极点架构，则仅仅相当于两个一阶低通滤波的串联，依然未脱离FOF方法的局限，因此，需采用两极点一零点的架构，其传递函数表达式可写为：

式中：a、b、c为滤波器参数。

引入二阶滤波器后，风电机组输出有功参考值Pref2变为：

二阶滤波器G2nd(s)自身的幅频特性（设b＜c＜a）如附录B 图B1 所示，可见G2nd(s)具有的3 个转折频 率 分 别 对 应ω1=b，ω2=ab/c以 及ω3=a。同样，以附录A 表A1 所示风电系统为对象，研究Gω/v-2nd(s)的幅频特性。根据上文理论及仿真分析，滤波器参数a、b、c的配置原则如下：

1）为充分彰显SOF 方法频段选择的区分度，分母转折频率之间需满足b≪a。其中，b值需取小，以衰减低频段的功率波动。但过小的参数b会导致输出功率总体幅值过度衰减，导致风电机组收益减少，因此也需要权衡风能捕获效率，最终选取b=0.05。

2）ω3=a作为最后的转折频率点，承担的是滤除高频波动任务，因此a不宜取得过大，且一般需要固定不动。具体可按实际需求选取，若目标为增强0.5 Hz 以上的功率平滑效果，则a的取值应为0.5×2π ≈3.14。

3）转折频率点ω2=ab/c与ω3=a之间需要维持一定的带宽，以确保对风速输入趋势的跟踪精度，从而在动态平滑功率的同时保证风能捕获效率。为简化计算，本文将参数c定义为与a+b的正比关系：

式中：Kc为比例系数。

设置比例系数的优势在于能消去一个变量，降低动态过程的调参难度。此外，在b≪a的条件下，由极限原理可知第2 转折频率ω2存在的上极限为b/Kc，即通过在线调整Kc参数值可对系统传递函数实现微调，提高湍流风况下的动态平滑效果。通过减小Kc，转折频率ω2将朝ω1方向移动以增强功率平滑效果。本研究中SOF 初值设置为Kc=0.5、b=0.05、a=3.14。

此时，依据输出功率与转速3 次方之间的SOF关系，可推导出风速到功率的传递函数为：

不同控制方式下，GP/v(s)的幅频特性对比如图3 所示，其中FOF 方法参数为τ=0.5，SOF 方法参数为Kc=0.5、b=0.05、a=3.14。由图3 可知，FOF方法增强了高频的滤波效果却放大了低频段功率振荡。相较于PSF 方法，SOF 方法则从低频段开始一直衰减，因此，在动态控制过程中，SOF 方法相较于FOF 方法拥有更好的平滑效果。

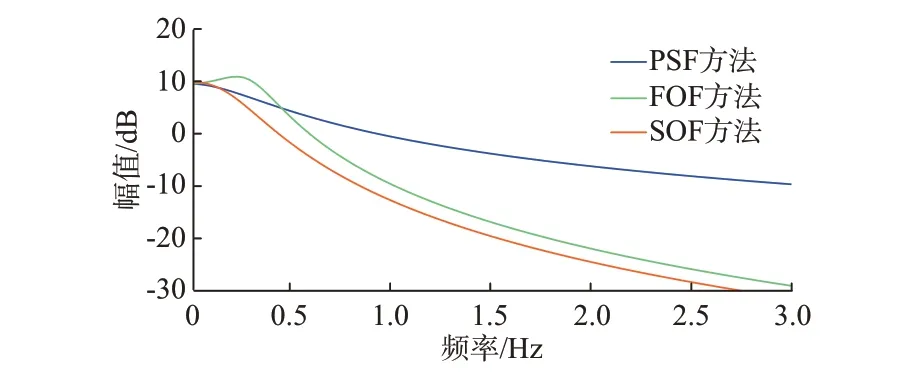
图3 SOF 和FOF 方法下GP/v(s)的Bode 图对比Fig.3 Comparison of Bode diagram of GP/v(s) with SOF and FOF methods

2.2 正弦风速输入下平滑能力验证

根据傅里叶变换理论，随机湍流风速序列可分解为若干正弦信号的叠加。对某风电场历史风速数据进行频谱分解，其快速傅里叶变换（FFT）结果如附录B 图B2 所示。从图中可以看出风电功率波动的大部分能量集中于0.5 Hz 以下的低频段。选取0.2 Hz 波动的典型正弦风速作为系统输入，以附录A 表A1 的系统参数为仿真对象，论证SOF 方法的平滑能力。该正弦风速vsin(t)如附录B 图B3（a）所示，其表达式为：

输出功率波形对比如附录B 图B3（b）所示。可观察到，在正弦波动的风速下，采用FOF 方法时发电机输出功率相较于PSF 控制反而波动幅度加剧，而SOF 方法能一定程度上衰减功率波动，该仿真结果与前文Bode 图理论分析一致。

2.3 低转速段的镇定保护

由文献［20］的分析可知，当风电机组运行于传统PSF-MPPT 控制时，系统总能保持稳定。为避免风速快速下降时，转子转速落入不稳定区，本文引入转速镇定保护措施，即当转速较低时，将有功参考值调整为MPPT 模式运行，待转速回升时再切换回平滑模式，具体切换机制如附录B 图B4 所示。

2.4 基于模糊控制的滤波参数在线调节

转子动能平抑波动的基本原理是在风速上升时，转子转速充分升高以存储动能，风速下降时通过转子减速释放能量进行补偿。因此，可根据风速幅度波动情况，风速发生大扰动时采用平滑效果较强的参数，而风速扰动不大时退回平滑效果较弱参数进行控制。本文提出的改进SOF 方法采用模糊逻辑控制器（fuzzy logic controller，FLC）对滤波系数进行在线修正。FLC 不依赖被控对象的精确数学模型，可模拟人的操作经验在线调参，已在动态特性不容易掌握的非线性风电系统控制中得到广泛应用［21-23］。

由于风速难以准确测量，本文基于转速和风速变化趋势的一致性，通过测量转速定义风速大扰动事件（风速大扰动示意图如附录B 图B5 所示）：当转速以较大加速度上升一段时间时，判断发生风速大扰动升高事件；同理，可判断风速大扰动下降。风速大扰动事件判断原理如图4 所示，实际控制时通常将相邻采样时刻的转速差值作为输入加速度信号，其中，判断加速度与持续时间的阈值可按经验与实际控制需求选取。此处，需要强调转子动能控制的非对称性：在引入滤波器的情况下会导致转速超调，在风速大幅升高时希望转速充分升高以存储动能，因此，滞环比较器输出为1；而风速大幅下降是危险信号，存在过度减速而失稳的风险，因此，滞环返回0 值。

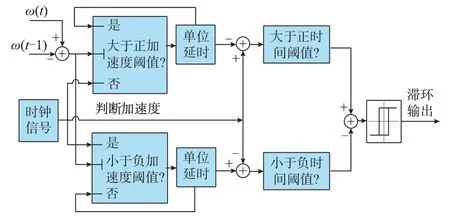
图4 风速大扰动事件判断原理图Fig.4 Judgment schematic diagram of large disturbance event of wind speed

将图4 中滞环输出结果（表征湍流状况）和转子转速信号（表征转子动能余量）分别作为输入信号1和2，采用T-S 型FLC 在线调整二阶滤波器参数Kc，构成双输入/单输出的模糊推理子系统，使用MATLAB/Fuzzy 控制工具箱进行模糊控制程序设计。输入隶属度函数如附录B 图B6 所示。图中：FLC 输入1 的论域范围为［0，1］（用N 代表未发生大扰动上升，Y 代表发生大扰动上升），输入2 论域范围为［0，1.2］（用标幺值表示，其中L 代表低转速，H代表高转速），模糊控制输出的Kc的论域范围为［0.3，0.5］。

建立附录B 表B1 所示模糊控制规则，以体现如下控制特征：

1）当未发生大扰动时，Kc维持初值；当检测到风速发生大扰动上升时（滞环信号为1），采用激进参数Kc调整到0.3，以使转子充分加速存储动能；

2）当检测到风速大扰动下降时，采用保守的参数，即将Kc修正回初值0.5；

3）此外，转子转速将触及运行上限时，根据当前滞环信号适当降低输出：处于大扰动上升过程中时，下调Kc为0.4；处于非大扰动上升过程时返回初值0.5，以避免转速越限而导致电磁功率突变。

由于本文方法中在低转速区以镇定方式维持转速稳定，转速信号隶属度划分中不再设置转速下限保护。在FLC 输出端口引入速率限制器，防止滤波器参数突变从而导致输出有功参考值突变。为了保证在使用本文所提出的控制策略下可有效实现输出功率的平滑外，兼顾滤波器调参的简便和实用，采用附录B 表B1 所示的模糊逻辑推理表。

3 基于改进转子动能控制策略的仿真验证

目前，主流风电机组单机容量从以前的2 MW已经上升到6～10 MW。为了证明本文所提功率平滑策略的有效性及与实际机组的契合性，本文首先进行了6 MW 风电机组的仿真。基于MATLAB/Simulink 平台建立附录A 表A1 所示参数下的仿真模型，对一阶滤波功率平滑控制策略以及改进二阶滤波功率平滑控制策略进行仿真对比分析。

3.1 FOF 方法的平滑效果验证

如附录C 图C1 所示，本文设置幅值变化较大的湍流风速（湍流强度A 级）进行仿真验证。首先，将选取不同时间常数τ下的FOF 控制与传统PSFMPPT 方法进行比较，仿真结果如图5 所示。由图5（a）可见，湍流强度大的风速波动下，基于FOF方法的功率平滑效果反而明显减弱。由于该湍流风速下低频大幅值波动占主导，FOF 方法虽然能平抑高频波动分量，但由于低频波动的幅值被放大，同样风速条件下相较于MPPT 控制反而会使输出功率的绝对波动幅值增大。由图5（b）可观察到，采用FOF 控制策略时，系统转速将偏离最大功率点，围绕MPPT 转速附近振荡。此外，伴随τ值增大，高频转速和功率波动幅值继续衰减，但低频波动幅值愈发增大，使得绝对功率波动范围进一步增大。该仿真结果与前文理论分析一致。

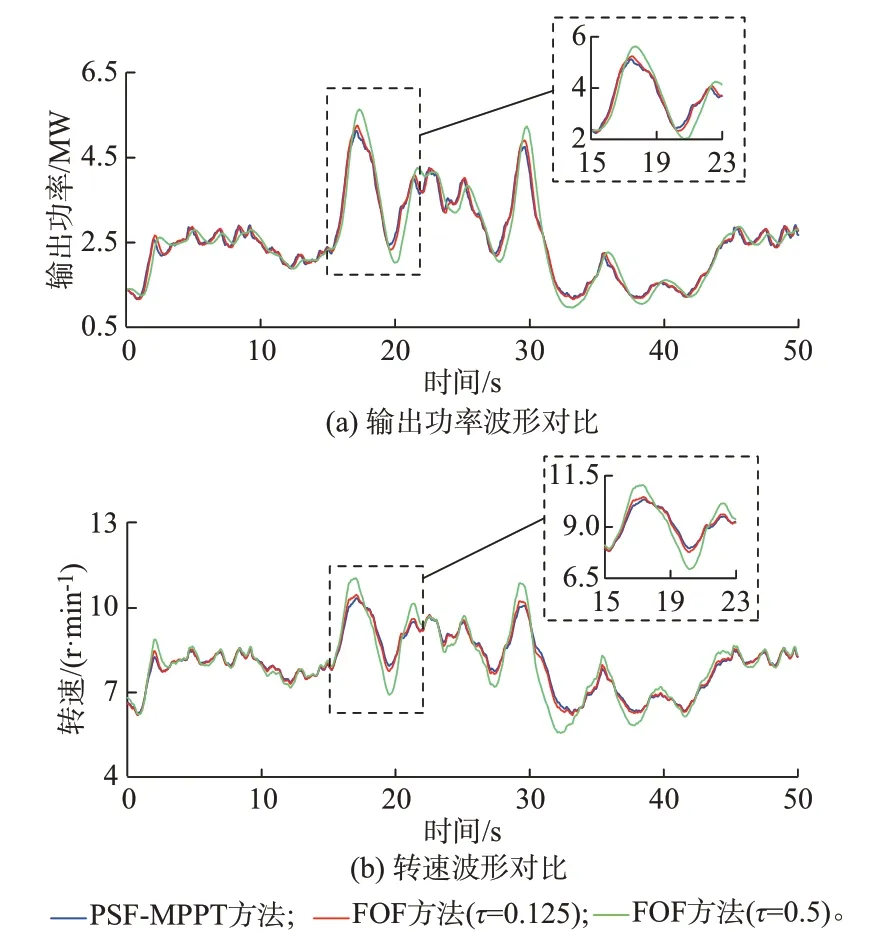
图5 FOF 方法仿真波形Fig.5 Simulation waveforms with FOF method

3.2 改进SOF 方法的功率平滑效果验证

图6（a）展示了本文所提出的改进SOF 方法的功率平滑提升效果。由于定参数SOF 方法不能适应变化的湍流风况，在风速快速降低时由于过度减速而落入不稳定区，出现较长时间的电磁功率跌落，其特征表现为：转速触及运行下限的同时，输出功率瞬间跌落，功率维持在较低水平的同时产生高频小幅波动；待风速重新升高时，转速回升，电磁功率跌落消除。由图6（b）的转速波形可以看出，相较于FOF 方法，SOF 方法通过转速更大范围的变动实现动能存储与释放。如图6（c）所示，当出现风速大扰动上升事件时，模糊控制子系统输出结果使Kc取值降低，以增强功率平抑效果。当风速快速降低时，通过转子镇定保护暂时回到MPPT 模式以维持低转速稳定性。相比于定系数的SOF 方法，避免了湍流强烈时出现的转速越限和电磁功率跌落现象。

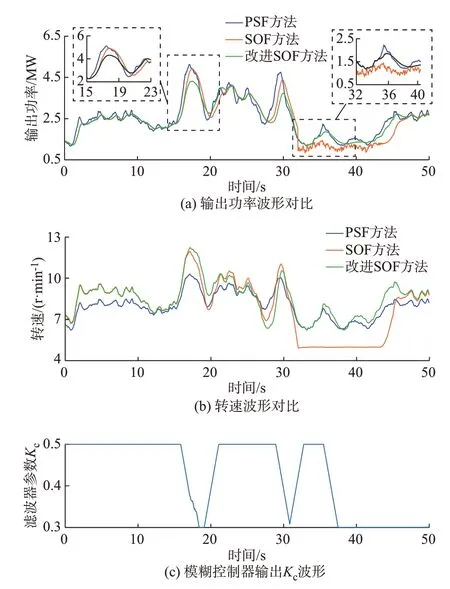
图6 SOF 方法仿真波形Fig.6 Simulation waveforms with SOF method

3.3 不同控制方式下的电磁转矩比较

在湍流风速下降低PMSG 电磁转矩脉动，对减轻风电机组机械轴系疲劳，延长使用寿命具有重要意义［14］。不同控制策略下的电磁转矩仿真结果如附录C 图C2 所示，从图中可见，采用FOF 转子动能控制时，容易加剧电磁转矩振荡幅度。而传统固定系数的SOF 控制策略虽能起到一定的抑制波动效果，但在大约32 s 时发生电磁功率跌落，此时转速触及下限，导致电磁转矩骤降，对传动轴造成巨大冲击，并且电磁转矩开始出现较长时间高频低幅值脉动，易对PMSG 寿命造成损伤。而与上述方法相比，本文提出的改进SOF 控制下的发电机电磁转矩脉动明显减小，证明了本文所提改进SOF 控制策略在有效平滑输出功率的同时，对电机转矩脉动抑制的有效性。

4 基于改进转子动能控制的实验验证

为了验证所提控制策略在实际工程应用的可行性，在实验室环境搭建了模拟千瓦级功率等级的永磁直驱风电系统实验平台，该实验平台基于RTUBOX204 控制器构建，见附录D 图D1。风电机组模拟平台由两台相同型号的4 对极永磁同步电机组成，考虑到伺服电机自身转动惯量较低，在传动轴上加装飞轮以增加系统转动惯量，电机控制架构见图D2。图中：PMSM1 作为风电机组模拟器，根据上位机给出的风速信号与传感器测得的转速信号产生对应的转矩；PMSM2 作为发电机。实验台对两台电机的控制指令由RTU-BOX204 数字控制器输出，实验参数见表D1。

实验所用风速序列和仿真风速相似，以模拟极端场景下的强湍流风况，风速波形见附录D 图D3。图D4 所示为FOF 控制与传统PSF-MPPT 控制下的实验波形对比，FOF 方法给出了两组不同一阶滤波参数τ控制下的结果。由图D1（a）所示功率波形和图D1（b）所示转速波形可观察到，采用FOF 方法尽管能达到抑制高频功率波动的效果。然而，引起的低频振幅加剧现象导致总体平滑度并未得到提升。此时，功率和转速围绕MPPT 转速附近振荡，且振荡幅度随一阶滤波参数τ值的增大而增加，与第3 章仿真结果吻合。

本文提出的改进SOF 方法与传统SOF 方法控制下的对比实验波形如附录D 图D5 所示，输出功率、转速波形分别如图D5（a）和（b）所示。从图中可看出，传统SOF 方法采用固定系数平滑且仅设置了转速下限保护，导致有限的转速运行区间内无法跟踪平滑指令，在32 s 处出现和仿真同样的电磁功率跌落现象。本文所提方法由于采用基于模糊推理的灵活参数调整策略，不仅总体功率波动范围限制在更低的水平，而且因为转速镇定保护措施的协调控制，全动态过程的功率平滑度都能得到保障。由此可以看出，所提的改进SOF 方法相较传统FOF 方法能同时有效平滑低频及高频波动分量。

附录D 图D6 所示为不同控制策略下电磁转矩实验波形，分别考虑了传统PSF-MPPT 控制、传统FOF 转子功能控制（τ=0.125，τ=0.5）、传统SOF 控制及改进SOF 控制。从实验波形中可看出，本文提出的改进SOF 控制在几种控制策略中电磁转矩脉动最低，证明了所提方法在平滑功率的同时能有效降低转矩脉动，可有效改善发电机在湍流风况下的运行状态，提高机组使用寿命。

需要说明的是，本文小功率风电机组模拟平台实验的主要目的是对所提改进SOF 转子动能控制策略的可行性及有效性进行验证，但由于实验平台的惯量有限，远小于实际大功率风电系统，实验效果没有仿真中明显。未来，随着风电机组单机容量的不断增加，本文所提出的功率平滑方法的优势将更加显著。

5 结语

本文提出了一种基于转子惯性动能和改进二阶滤波器的风电机组输出功率平滑控制策略，仿真和实验验证了控制策略的有效性，本文主要研究结论如下：

1）通过比较转速环级联一阶/二阶滤波器的转子动能控制策略，依托系统传递函数进行功率平滑的理论分析，从频域角度阐释了FOF 方法的局限性，深入分析了SOF 方法用于风电机组利用转子动能平滑输出功率的原理，并首次提出了二阶滤波器参数的配置原则。

2）在理论分析基础上，本文提出了一种改进转子动能功率平滑控制策略。提出了基于模糊控制的在线调整二阶滤波器参数方法，以提升风速动态变化过程中的功率平滑效果，并通过加入镇定保护措施维持湍流输入下风电机组转速稳定性。仿真与实验结果表明，所提出的改进SOF 方法能在进一步平抑输出功率波动的同时有效抑制发电机电磁转矩脉动。

3）本文提出的基于模糊逻辑的改进SOF 转子动能控制方法重点关注功率平滑的有效性，不涉及最优化方法，具有一定的局限性。后续可深入研究的方向是根据风电机组状态信息、湍流风速输入特征以及风电机组并网运行约束，探究考虑平滑效果和风能捕获效率的最优控制率。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。