火灾条件下隧道混凝土路面温度与力学响应研究

马立军,徐 璐,王 静,张云龙,钱雪松

吉林建筑大学 交通科学与工程学院,长春 130118

0 引言

隧道属于半封闭建筑,空间狭小,发生火灾时温度急剧上升,烟雾无法扩散,这不但会造成人员伤亡,还会对结构产生不可估量的危害[1],因此需要对隧道路面火灾进行研究.由于隧道火灾试验所需的空间较大,试验难以控制且存在一定风险,常采用有限元模型模拟火灾的发生[2].

近年来,相关学者对隧道火灾响应进行了一系列研究.对于数值模拟,学者们主要分析了隧道温度分布及隧道内部温度变化.朱合华等[3]人根据有限单元法对比分析不同标准火灾曲线下的温度分布,表明衬砌的内部温度分布受火灾曲线的影响较大,不同火灾曲线下的温度分布具有较大差异.刘晓勇[4]同样采用有限元法分析了偏压条件下的衬砌内部温度分布,结果表明衬砌的内部温度变化是由曲线变化转为直线变化,同时当偏压角度较大时,火灾将成为隧道破坏的诱导因素而非直接因素.Liu B等[5]人对海拔高度对隧道火灾纵向温度分布的影响进行研究.结果表明当海拔温度升高时,烟与隧道壁之间的热对流增强,从而增加了烟的热损失,故高度较高时,纵向温度衰减更快.隧道发生火灾除了对建筑结构的威胁,还会产生大量浓烟,对人们的生命安全产生威胁.Król A等[6]人在长度为678 m、倾斜4 %的实际公路隧道中进行了热烟试验.结果表明,隧道的整个背风面都充满了热气,这对困在该区域的人来说是致命的威胁.与此同时,在纵向通风隧道中,气流结构及其大小对烟气管理非常重要.Se C M K等[7]人采用计算流体力学技术,研究了不同尺寸、方向和性质下的火源对气流速度和温度分布的影响.结果表明,火源性质对整个隧道的上游风速和气流模式产生不利影响.隧道内属于封闭空间,一旦发生火灾,可能会引起周围车辆及建筑物起火,形成多处火源,因此崔心源等[8]人对双火源隧道火灾进行模拟,结果表明与单火源相比,双火源之间的相互影响更易造成浓烟的积聚,增大了危险性.此外,双火源之间的距离对温度也有一定影响,当火源间距增大时,辐射强度在降低,但仍会对人员及建筑物造成危害.

结合上述文献可知,目前隧道火灾的研究主要集中在火灾对衬砌的影响以及隧道内烟气排放[9-10],关于火灾对隧道混凝土路面的影响研究较少,本文以有限元软件建模,研究了隧道路面在火灾下的响应变化,为以后隧道路面火灾的研究提供参考.

1 路面模型建立

1.1 模型尺寸

为了更好地模拟隧道路面实际情况,使模拟的数据结果更加真实有效,按照1∶1的比例采用Ansys软件建立三维有限元模型如图1所示.隧道纵向长度取20 m,隧道半径4.5 m,隧道高为7.55 m,路面层厚度为30 cm,断面如图2所示.建立模型时以隧道入口平面为xoy平面,竖向为y方向,向上为正,横向为x方向,向右为正,沿隧道纵向为z方向.火灾发生在路面10 m～12 m处,火灾持续时间为2 h.在热分析过程中,采用可用于瞬态热分析的3D实体热单元Solid70,在热-结构耦合分析时采用与之对应的Solid65单元.

图1 结构三维有限元模型全图

图2 隧道路面断面

1.2 材料参数

在隧道火灾模拟计算时,导热系数、比热容、温度线膨胀系数等数值会随着温度和时间的改变而变化,因此需要确定热工参数来进行结构的温度与应力的分析.在隧道火灾过程中,路面混凝土随着温度的升高体积膨胀.部分水分挥发,导致混凝土的密度减小.模拟中所采用的比热容和导热系数的选取参考欧洲规范[11]计算公式如式(1)和式(2)所示.线膨胀系数采用试验研究得到的混凝土函数公式(3).但与其他混凝土参数相比,密度变化较小,因此将混凝土的密度设为与温度无关的常量,取值为2 400 kg/m3,泊松比取0.2[12],混凝土的热力学参数见表1.

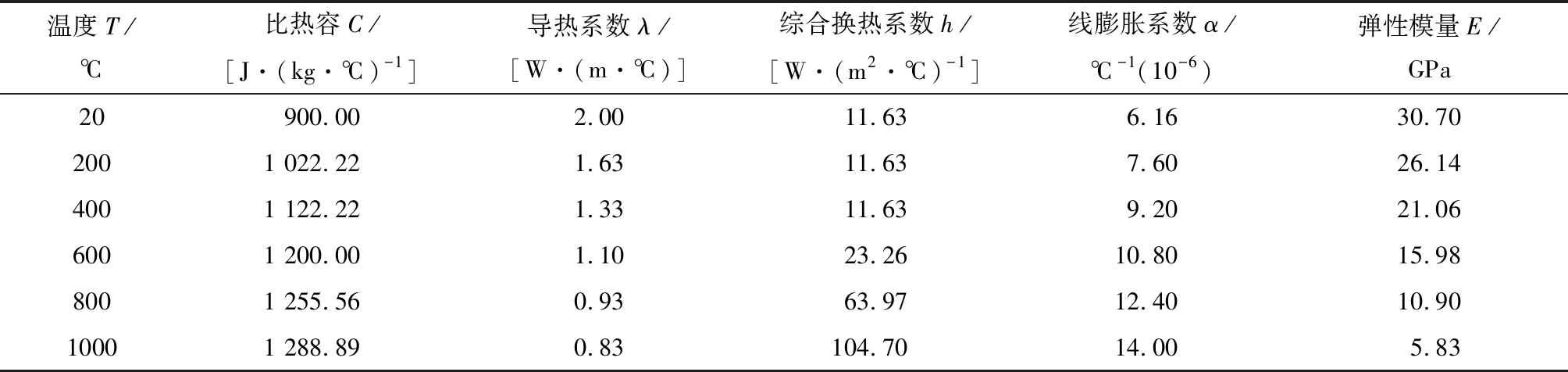
表1 混凝土的热力学参数

(1)

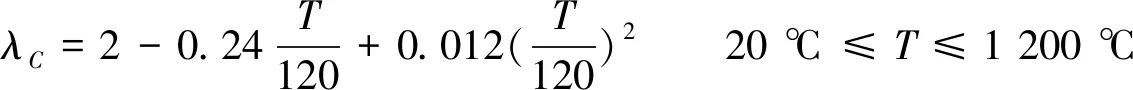
(2)

αC=(0.008T+6)×10-620 ℃≤T≤1 200 ℃

(3)

1.3 假定条件

(1) 混凝土在进行高温条件下的结构设计和计算时是各向同性材料.路面为完全均匀和各向同性的连续.

(2) 混凝土在经历高温或火灾时,自身不释放和吸收热量,热量保持不变.

1.4 边界条件

第1类边界条件也称为温度边界条件

T|Γ=T0;T|Γ=f(x,y,z,t)

(4)

式中,Γ为物体边界;T0为已知温度,℃.

第2类边界条件也称为热流边界条件

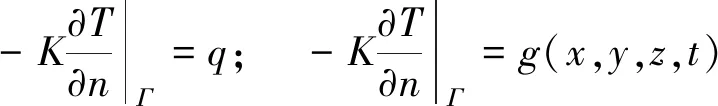
(5)

式中,Γ为物体边界;q为热流密度(常数);K为材料的热导系数,W/(m·℃).

第3类边界条件也称为对流换热边界条件

(6)

式中,Tf为流体介质温度,℃;α为换热系数,W/(m2·℃).

本文采用第3类边界条件,假定隧道内为一个均匀的温度场,内部温度相同,采用常温20 ℃.隧道的围岩常处于山体之中,外界空气、气流等因素对其影响甚小,据文献[13]研究结果表明,当隧道路面发生火灾时,温度无法传递至围岩附近,因此,忽略围岩对隧道路面应力产生的影响.此外,隧道自重的施加采用方式为对整体结构施加重力.

1.5 加载温度

由于公路隧道火灾通常是以碳氢为主的混合火灾,加载温度曲线采用《建筑设计防火规范》(GB50016-2014)[14]推荐的HC升温曲线如公式(7)所示.

T=T0+1 080×(1-0.325×e-0.167×t-0.675×e-2.5×t)

(7)

式中,T为实时温度,℃;T0为初始温度,℃,取T0=20 ℃;t为火灾持续时间,min.

2 结果与讨论

2.1 温度分布

2.1.1 纵向温度分布

发生火灾时,高温会造成隧道内车辆的引燃及周围管道设施的破坏,甚至导致人员受伤.同时,考虑到隧道火灾温度升高极快的特点,在模型中模拟隧道火灾发生,观察隧道火灾后2 h内路面的温度变化.

沿隧道纵向温度随距离分布云图如图3所示,中心区域为火灾中心位置,温度最高,可达1 035.86 ℃.随着与火灾中心距离的增加,区域颜色逐渐变浅,说明温度在逐渐向外传递,热量逐渐向两侧延伸.在达到一定距离后颜色变为浅色,此时温度已接近常温,说明超过此范围火灾将无法对隧道路面结构造成影响.为了更加直观地观察隧道路面纵向温度,将数据进行整理,绘制纵向分布的温度随时间变化曲线,如图4所示.图4显示,在火灾中心处温度达到最高为1 035.86 ℃,这与温度云图一致.随着温度沿路面的扩散,在火源两侧大致呈对称分布,这是由于随着距离的增加,高温区域的烟雾不断向低温区域扩散.随着距离远离火灾中心,升温速率逐渐降低,温度也随之降低.在4 m～8 m处曲线较为平缓,温度缓慢增加;在8 m～10 m处曲线斜率急剧增加,温度急速上升,这是因为8 m～10 m更接近于火源中心位置,温度扩散速率更快,温度变化更剧烈.

图3 沿隧道纵向温度随距离分布云图

图4 沿隧道纵向温度随距离分布曲线

2.1.2 深度温度分布

当发生火灾时,隧道结构受到破坏,无法正常使用,会造成一系列问题,因此研究隧道火灾对路面结构的破坏程度,观察其深度方向的温度分布十分必要.

图5为隧道路面深度方向温度分布.由于混凝土的导热惰性,当深度逐渐加深时,热传递速率逐渐降低,温度随之降低.当达到路面底层,即距离路表面300 mm时,温度已接近常温状态且保持稳定,因此可以忽略隧道路面火灾对路面以下隧道衬砌结构的影响.由图5可知,随着深度的逐渐增加,温度下降由非稳定阶段转变为稳定阶段,具体分为急剧下降阶段、平缓下降阶段以及趋于稳定阶段的状态.从路表到距离路表50 mm处温度变化明显,为急剧下降阶段,此后温度变化速率逐渐降低,进入稳定阶段,在此阶段热量被消耗殆尽,路面底层混凝土层趋于常温.

图5 深度方向路面温度随距离变化

图6给出了火源中心处路面厚度方向的温度云图.由图6可知,最高温度出现在路表面可达1 035.86 ℃,这与隧道纵向最高温度一致,再次证明了模拟的正确性.随着路面深度的增加,温度云图颜色逐渐变浅,温度逐渐降低.

图6 深度方向路面温度云图

图5中,混凝土在距离路表100 mm处的温度约为128 ℃,当温度超过200 ℃时才会对混凝土的工作性能产生影响,故只对距离路表100 mm以内的隧道混凝土路面进行分析.图7中给出在遭受火灾区域内路面不同深度位置下温度随火灾时间的变化曲线.其中H0表示路面表面,H50表示距离路面表面50 mm,H100表示距离路面表面100 mm.

从图7中可知,随着路面深度的增加,温度逐渐减小,同时各深度层面表现出相同的趋势,即随时间的增加温度不断上升.当火灾发生在路表面时,温度增长随时间变化较快,当深度逐渐增大,温度随时间的变化逐渐减小.在火灾发生的路表面上,温度增长较快,随时间的增加温度可超过1 000 ℃.与表面相比,当距离火灾深度达到50 mm时,温度随时间的增加大幅度减小,当深度达到100 mm时会发现温度没有明显上升,基本保持在常温.

2.2 温度应力分析

热应力,是发生温度变化的物体与不能自由伸缩的其他物体之间产生的约束力,或是发生温度变化的物体内部之间相互约束所产生的应力[9].当隧道发生火灾时,由于隧道内部温度急剧上升,导致热应力迅速增加,容易降低结构的可靠性和安全性.

2.2.1 纵向应力分布

为了评价隧道路面在火灾作用下的应力分布情况,本文综合考虑了第一主应力、第二主应力、第三主应力.基于第四强度理论,对火灾下混凝隧道路面的Mises应力进行分析.图8为隧道混凝土路面在纵向方向和沿路面深度方向的Mises分布曲线.

图8 沿隧道方向等效应力分布

由图8可知,在火源中心处,Mises应力最大为109.22 MPa,这是由于此处温度最高,导致此处的温度应力最高.随着距离火源中心位置距离的增加,Mises应力逐渐降低,温度也随之降低,由此产生的温度应力逐渐降低.此外,Mises在火源中心位置两侧大致呈对称分布,这与前面的温度分析结果一致,从而再次证明了模拟的正确性.图9给出了隧道纵向的Mises应力云图,由图9可知,在隧道纵向云图颜色逐渐变浅,对应的最大Mises应力逐渐降低,其中最大应力出现在火源中心位置.

图9 沿隧道方向等效应力云图

2.2.2 深度方向应力分布

图10给出了火源中心位置隧道深度方向的Mises分布曲线.由图10可知,最大Mises应力出现在隧道路面表面,这是由于此处直接与火源接触,使得该位置的温度最高,温度应力最大.由于Mises综合考虑了第一主应力、第二主应力及第三主应力,因此在图10中最小Mises应力并非出现在隧道路面底层,而是在路基路面表面87.5 mm处,此后Mises应力逐渐趋于稳定.由此可见,在此范围内火灾对隧道路面产生了巨大影响,而超过此范围,温度对路面的影响逐渐降低,这与前面温度分析结果85 mm基本一致.但由于隧道路面受自身自重、环境外力等的综合影响,故Mises最小值与对混凝土物理力学性能影响可忽略的深度不完全相同,而是具有相同趋势.

图10 深度方向等效应力分布

图11给出了隧道路面深度方向的Mises应力云图.由图11可知,最大应力出现在路面表面,这与前面分析一致.此外,由于路面与隧道接触点出现应力集中现象,导致Mises应力高于其他地方.

图11 深度方向等效应力云图

3 结论

(1) 发生火灾时,火源中心处的温度最高且可达1 035.86 ℃.随着距离火源中心位置距离的增加,温度大致在火源中心两侧呈对称分布.在4 m～8 m处温度升高较为平缓,在8 m～10 m处温度急剧上升,距离火源中心处热量的剧烈波动在短时间内温度达到峰值,

(2) 在隧道路面深度方向,由于混凝土的导热惰性,随着深度的增加,温度逐渐降低,路面表面温度在50 min内达到最高温度且保持稳定;在H50范围内温度近似于线性增加,升温较慢且最大温度远低于路面表面,在路面底层已接近常温且保持不变.

(3) 发生火灾时,隧道路面Mises应力最高出现在火源中心处,可达109.22 MPa,与温度分布趋势相同.在路面深度方向,Mises应力在0 mm～87.5 mm范围内保持下降趋势,但在87.5 mm处应力出现转折,Mises应力在此之后增加并保持稳定.