深度学习方法在地震事件分类中的应用及可解释性研究

路晓辰 杨立明 杨兴悦 王祖东 王维欢 高永国 尹欣欣

摘要：

采用2016—2020年福建臺网所记录的爆破和天然地震事件以及背景噪声数据集，使用CNN模型、Inception10模型、ResNet18模型和Vgg16模型4种深度学习网络模型进行分类研究。针对深度学习网络模型的“黑盒”问题，将梯度类激活映射（Gradient-weighted Class Activation Mapping，Grad-CAM）算法引入这4种分类模型中，得到每个模型的可视化图。通过可视化图可以直观地看出模型在做出分类决策时对于不同波形特征的依赖权重，为模型的可解释性提供依据，进而提高模型的可信度。通过对模型的可视化图分析得出，分类效果更好的CNN模型和Vgg16模型在做出决策时更依赖于地震波形的震相特征，对于震前和震后的波段关注较小;而ResNet18模型和Inception10模型对于震相特征的关注不够敏锐。通过Grad-CAM算法对模型进行可视化分析得到的结果能够很好地反映模型的分类效果，对于改进和选择合适的分类模型具有重要意义。

关键词：

可解释性; Grad-CAM算法; 爆破事件分类; 深度学习

中图分类号： P315.63      文献标志码：A   文章编号： 1000-0844（2023）02-0474-09

DOI：10.20000/j.1000-0844.20220926001

Application and interpretability of deep learning

methods in seismic event classification

LU Xiaochen1，2， YANG Liming3， YANG Xingyue2， WANG Zudong2，

WANG Weihuan2， GAO Yongguo2， YIN Xinxin2

（1. Lanzhou Institute of Seismology， CEA， Lanzhou 730000， Gansu， China;

2. Gansu Earthquake Agency， Lanzhou 730000， Gansu， China;

3. Qinghai Earthquake Agency， Xining 810000， Qinghai， China）

Abstract：

In this paper， four deep learning network models， i.e.， the CNN， ResNet18， Vgg16， and Inception10 models， were used to classify blasting and seismic events， and the dataset used blasting events and natural seismic events recorded by the Fujian station network from 2016 to 2020. The gradient-weighted class activation mapping （Grad-CAM） algorithm was introduced into the four classification models to address the “black box” problem of deep learning network models， and a visualization of each model was obtained. The visualization diagram provides an intuitive view of the model's reliance weights for different waveform features when making classification decisions， thus providing a basis for the models interpretability and improving its credibility. Analysis of the visualization diagram shows that the CNN and Vgg16 models with better classification effects rely more on the seismic phase characteristics of seismic waveforms when making decisions and pay less attention to the pre-earthquake and post-earthquake bands. In contrast， the ResNet18 and Inception10 models are insufficiently sensitive to the seismic phase characteristics. The results obtained from a visual analysis of the models through the Grad-CAM algorithm well reflect the classification effect of the models， which is important for improving the models and selecting an appropriate classification model.

Keywords：

interpretability; Grad-CAM algorithm; classification of blasting events; deep learning

0 引言

从创建地震灾害的构造事件目录到监测核爆炸，区分爆炸和地震仍然是地震学中的一项重要任务。由于爆破和地震事件的波形具有相似性，如果人工区分较多的爆破和地震事件需要花费大量的时间，而且区分过程中个人的主观性比较强。传统方法主要通过提取震相特征去区分爆破和天然地震事件，比如提取波形数据的初动方向、P波和S波最大振幅比、尾波衰减等特征［1-3］，或者使用傅里叶变换、小波变换等方法提取波形数据的频域信息进行分析［4-5］。区分爆破和天然地震事件的传统方法只是提取了事件波形中的部分特征，然后通过单个或多个震相特征去分类地震事件，这些方法会造成震相特征的损失，不能够将整个波形的特征利用起来，从而会降低分类精度。最近深度学习在地震学各个领域应用广泛，例如应用在到时拾取、地震事件分类、地震目录的构建等。2020年Mousavi等［6］提出EQTransformer深度学习模型，用于同时进行地震检测和相位选取。通过使用分层注意力机制，结合地震信号的相位和全波形的信息，提高了每个单独任务的模型性能。2021年赵明等［7］将PhaseNet震相识别算法、REAL震相自动关联技术与传统定位技术VELEST和HYPODD相结合，自动构建长宁地震前震目录。2022年高永国等［8］使用深度学习卷积神经网络方法搭建两个不同的模型，对甘肃地区的地震事件和爆破事件进行了分类研究。

虽然深度学习广泛应用于地震学研究、图片分类、自然语言处理及目标识别等领域，而且具有其独特的优势，但是深度学习网络模型作为一个黑盒模型缺乏可解释性，研究人员无法理解深度学习模型如何做出决策，限制了深度学习的应用和发展［9］。对于一些分类任务来说，较高的识别率并不代表模型能够正确地捕捉到目标本身的特征。在文献［10］中提到了华盛顿大学所做的一项实验，华盛顿大学曾通过创建一个分类器来识别哈士奇与狼，但实际上模型是依据背景中是否存在积雪来做出的决策，而不是通过哈士奇和狼的本身特征来进行识别的。对于应用到地震事件分类中的模型来说，模型可能关注的主要特征为事件的位置和时间信息，而不是波形的真正鉴别特征，如初至波、波峰和尾波［11］。所以在爆破事件的分类研究中，加入对深度学习网络模型的可解释性分析具有重要的意义。随着可解释性方法的不断提出和发展，深度学习的可解释性研究已经应用于多个领域。Zhang等［12］提出MDNet模型，该模型在医学图像和诊断报告之间建立直接的多模态映射，而且可以将诊断报告的决策依据进行可视化。李玮杰等［13］利用归因方法进行雷达图像深度学习模型的可解释性研究。目前，在地震学中对于深度学习的可解释性研究较少。

本文使用了4种深度学习网络模型进行爆破和天然地震事件的分类，而且将梯度类激活映射（Gradient-weighted Class Activation Mapping，Grad-CAM）算法引入到分类模型中，尝试解决地震事件分类模型的“黑盒问题”。通过加入分类模型的可解释性研究，提高了模型的可信度，建立了人与机器之间的信任，推动了深度学习应用到实际的地震事件分类工作中去。可解释性研究提高了模型的透明度，通过可视化图可以了解到模型学习到的震相特征，为选择模型、诊断模型、修改模型及应用模型提供了依据。

1 数据与方法介绍

1.1 数据集

本研究选取2016—2020年福建台网所记录的爆破事件和天然地震事件，从中去筛选其中的爆破事件和天然地震事件。截取每个事件的三通道波形，波形的开始时间为最近台站P波到时的前2 s。每个通道截取20 s波形，波形采样率为100 Hz，每段波形取2 000个点。选取每个事件震中距较小的台站，以保证在20 s的时间窗中能完整记录P波和S波。经过筛选得到9 794个天然地震三分量波形和5 244个爆破三分量波形，并加入7 000条三分量噪声数据。最后对所有的波形数据进行归一化处理。随机打乱数据集的顺序，将前20 000条三分量波形作为训练集，剩余2 038条三分量波形作为验证集。最终得到的训练集包括8 914个天然地震三分量波形，6 317个噪声数据，4 769个爆破数据。将没有加入训练集的2 038条三分量波形作为验证集，验证集包括880个天然地震数据，683个噪声数据和475个爆破数据。

1.2 深度学习模型

本文采用4种深度学习网络模型进行地震事件和爆破事件的分类，包括CNN模型、ResNet 18模型、Inception 10和Vgg16模型（图1）。

CNN模型主要包含5层二维卷积层，卷积核大小为3×1，卷积深度依次为16、32、64、128、256。模型的输入尺寸为2 000×1×3，模型使用卷积神经网络从输入的三分量波形中自动提取特征。通過CNN（卷积神经网络）层提取的特征被FC（全连接）层扁平化为100个特征，然后通过最后的全连接层进行分类。

ResNet模型利用残差结构解决了深度网络出现的梯度消失、梯度爆炸等模型退化问题［14］。ResNet模型选取经典的ResNet 18模型，一共使用4个残差块，每个残差块具有两个3×3卷积，模型主要包括17个卷积层和1个全连接层。

Inception结构能够增加网络的深度及宽度，而且减少了模型的训练参数个数，解决了深度网络计算参数过多造成的过拟合和梯度消失等问题，从而提升了模型的性能［15］。Inception10模型主要采用Inception-v1模块，具有1×1、3×3和5×5三种卷积核。

Vgg16模型包含13个卷积层和3个全连接层［16］。整个网络都使用3×3的卷积核尺寸和2×2的最大池化尺寸。

1.3 Grad-CAM算法

为了解决深度学习网络模型的可解释性问题，学者们提出了很多解决方法。可解释性方法可以分为事前可解释性方法和事后可解释性方法。事前可解释性指模型本身具备解释能力，事后可解释性指使用特定方法去解释训练好的模型。曾春艳等［17］将深度学习可解释方法总结为自解释模型、特定模型解释方法、不可知模型解释方法及因果可解释性4大类。

自解释模型指本身具有可解释性的模型。典型的自解释模型有线性回归模型［18］和决策树模型。特定模型解释方法通过研究模型的内部结构和参数来解释模型，主要方法有激活最大化方法、基于梯度解释方法及类激活映射方法。Erhan等［19］2009年提出了激活最大化分析法来可视化深度神经网络（DNN）学习到的高层特征。2016年Sundararajan等［20］提出积分梯度方法解决了神经元和网络饱和问题。2015年Zhou等［21］提出类激活映射技术，将深度学习网络中的全连接层替换为全局平均池化层（Global Average Pooling，GAP），对最后一个卷积层每个特征图的均值进行加权求和，最后通过热力图的形式对网络模型进行可视化。2017年Selvaraju等［22-23］提出了梯度类激活映射Grad-CAM算法。不可知模型解释方法是指不研究模型的结构和参数，仅通过模型的输入和输出来对模型进行解释。典型的不可知模型解释方法有LIME方法和LEMNA方法。因果可解释性方法主要从因果关系的角度分析模型做出决策的原因，可以从基于模型的解释、反事实解释、决策公平性三个方面对因果可解释性进行总结。基于模型的解释指分析模型中的组成部分对模型做出决策的因果影响。反事实解释描述了一种因果关系“如果没有发生x，那么y就不会发生”。决策公平性是指某些敏感特征的不同取值不应该影响模型的预测结果。

对于深度学习模型的可解释性，本文使用模型梯度类激活映射算法。Grad-CAM是类激活映射（Class Activation Mapping，CAM）的一种改进算法。其使用卷积层的梯度值来计算权值，从而不需要模型具有GAP层，改进了CAM算法需要更改模型结构、重新训练等局限性。Grad-CAM算法首先计算c类的输出分数yc相对于最后一个CNN层特征图Ak的所有像素的梯度平均值，其中k代表第k个特征图，式（1）定义了第k个特征图对于类别c的权重值αck。

αck=1z∑ui∑vjycAkij （1）

式中：ycAkij为最后一个卷积层中每一个特征图的梯度值;u和v是特征图的宽度和高度;Akij表示第k个特征图中坐标是（i，j）的像素点的像素值;z表示特征图的像素点的个数。在模型做出决策之前，由目标类c的这些权重给出了每个特征映射的相对重要性。然后利用式（2）计算出类判别定位映射：

LcGrad-CAM=RELU（∑nkαckAk） （2）

式中：n為最后一个卷积层中特征映射的总数;αck为权重值。因为只需要对目标类有积极影响的特征，所以将ReLU层应用于加权特征映射的线性组合。导出的定位图是最后一个特征图在同一维上的所有特征图的非负加权平均值，利用双线性插值对输入图像分辨率进行上采样，形成最终的热图。计算出的Grad-CAM权重归一化到0～1的范围，权重值越高，说明该震相特征重要性越大。每个模型均使用网络模型的最后一个卷积层来形成可视化图。

2 训练结果及评价指标

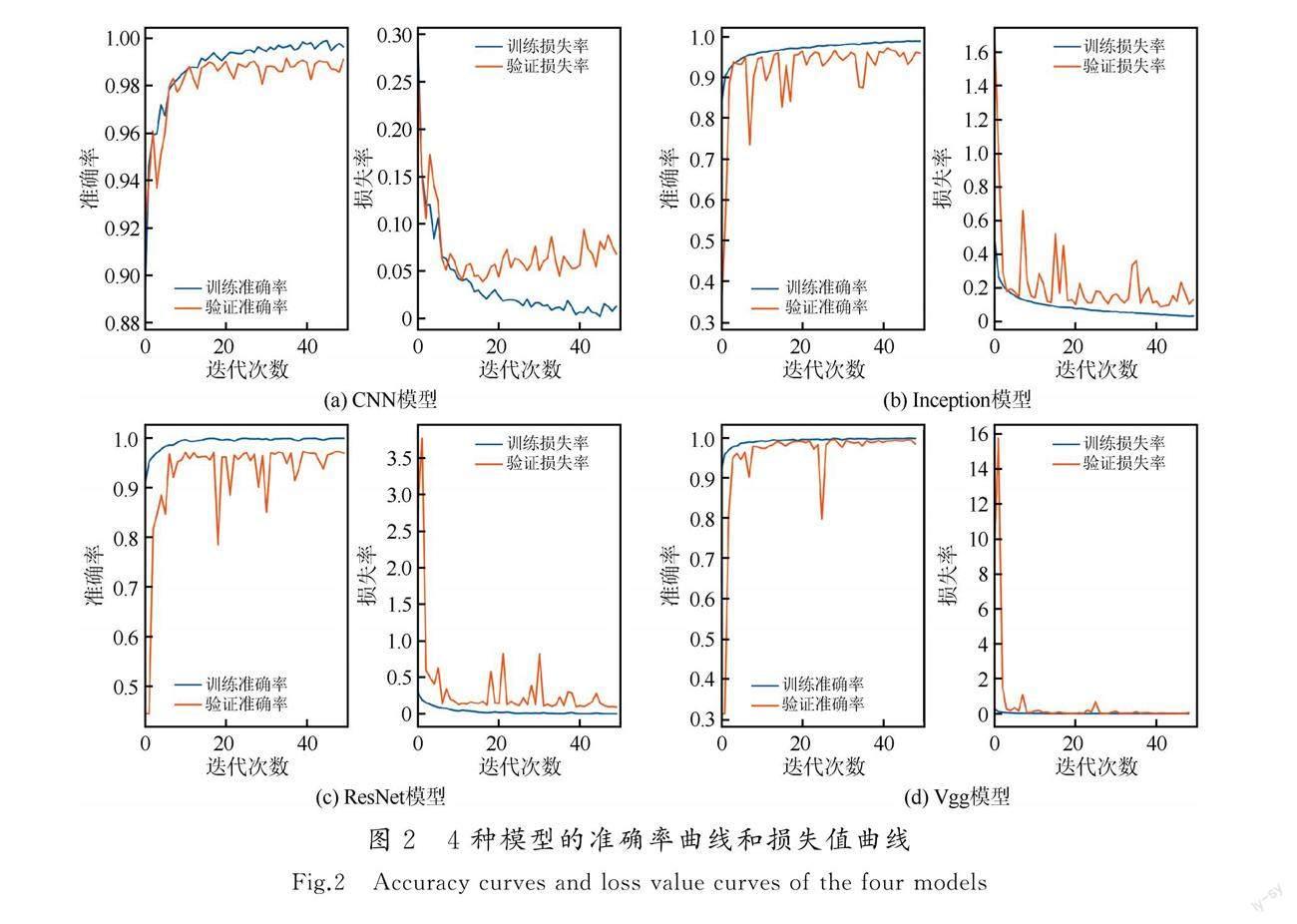
训练集包括8 914个天然地震三分量波形、6 317个噪声数据及4 769个爆破数据，将训练集分别应用于这4种模型中。在所有的训练中，均使用SparseCategoricalCrossentropy作为损失函数，Adam作为优化方法［24-25］。训练过程采取早停机制，若测试精度连续20个批次没有增长，则停止训练，并通过ModelCheckpoint函数保存训练过程中最优的训练模型。每个模型的输入尺寸均为（2 000，1，3），迭代次数为50，批尺寸为64。4种模型训练过程中的准确率曲线和损失曲线如图2所示。CNN模型在第15次迭代之后训练准确率曲线和验证准确率曲线趋于稳定，训练准确率稳定在0.99左右，验证准确率稳定在0.98左右。CNN模型的损失函数在第15次迭代之后走势趋于平稳，训练损失曲线稳定在0.02左右，验证损失曲线稳定在0.05附近。Inception10模型在训练过程中训练准确率曲线和验证准确率曲线迅速达到0.9以上，在第20次迭代之后趋于平稳，验证损失曲线在第20次迭代之后也稳定在0.2附近，训练损失曲线稳定在0.1附近。ResNet18模型在第5次迭代之后训练准确率和验证准确率均达到0.95以上，之后随着迭代次数的增加准确率趋于平稳。Vgg16模型在第5次迭代之后准确率曲线和损失曲线趋于平稳。

最终的训练结果如表1所列。CNN模型验证准确率高达99.17%，训练准确率为99.70%。CNN模型不仅分类精度较高，而且训练所用的时间也比较短。Inception10模型验证准确率为97.22%，训练准确率为98.76%。ResNet18模型验证准确率高达97.27%，训练准确率为99.81%。4种模型中Vgg16模型的验证准确率最高，达到99.20%，同时其训练准确率在4种模型中也相对较高，达到99.48%。由于Vgg16的模型参数达到31 511 363个，所以训练所用的时间相对较高。

测试集选取训练过程中未使用过的880个天然地震数据、683个噪声数据和475个爆破数据，使用训练好的模型对测试集中的地震事件进行分类。CNN模型和Inception10模型的测试集分类准确率分别为98.68%、97.55%。ResNet18模型的测试集分类准确率最低为96.71%。Vgg16模型的测试集分类准确率最高，达到99.07%。4种模型的测试集分类准确率均大于96%，说明4种模型的泛化能力都比较好。

准确率是一个比较直观的评价分类器效果的指标，但是在样本不均衡的情况下并不能作为很好的指标来衡量结果。为了评估每个模型的性能，本文加入查准率、召回率和F1值去评价每个模型的分类效果［26］。F1值为查准率和召回率的调和平均值，以便更好地反映模型的整体性能。

通过测试集来计算各个模型的查准率、召回率和F1值来评价模型的性能。从表2中可以看出4种模型的查准率、召回率和F1值均接近1，所以各个模型的分类性能比较好。

3 模型的可解释性研究

本文将Grad-CAM算法应用到模型的可解释性研究当中。计算出的Grad-CAM权重值归一化到0～1的范围，值越高说明重要性越大。CNN模型和Vgg16模型做出分类决策主要依赖P波和S波。ResNet18模型和Inception10模型的关注点较少，整条波形的高权值部分较少。

4种模型识别天然地震事件的可视化图如图3所示，每个子图显示了模型做出分类决策所依赖的波形特征，波形特征的Grad-CAM权重值越大，代表模型做出决策时更加依赖此波形特征，每个波形图的标题显示了波形的真实类别、预测类别以及预测概率，输入波形的真实类别为天然地震事件。4种模型预测此输入波形为天然地震事件的概率均为1，预测此输入波形为噪声数据或者爆破事件的概率为0。CNN模型在识别天然地震波形时主要依赖于P波和S波，权值在S波之后显著下降。Vgg16模型和CNN模型相似，同样将注意力放在P波和S波的震相上面，对于其他位置的关注度很低。ResNet18模型更关注S波，对于P波的依赖较小。Inception10模型对于S波的关注度较大，分类时对于其他波段的关注度较小。

4种模型识别爆破事件的可视化图如图4所示，输入波形的真实类别为爆破事件波形。Inception10模型预测输入波形为爆破事件的概率为0.97，波形为天然地震的概率为0.03，波形为噪声数据的概率为0。CNN模型、Vgg16模型和ResNet18模型预测输入波形为爆破事件的概率均为1。CNN模型识别爆破事件权值在P波和S波处最大，对于震前和能量衰减阶段的关注度非常低，主要注意力集中在能量较高的部分。Vgg16模型识别爆破事件时P波的权值最大，随后权值开始降低。ResNet18模型的关注点相对较少，仅仅关注到部分P波和S波的震相特征，在波形的末尾处有权值较高的部分。Inception10模型最大注意力在S波振幅较大处，整条波形的权值比较平均。

图5为4种模型识别噪声数据的可视化图，输入波形的真实类别为噪声数据。4种模型预测输入波形为噪声数据的概率均为1。CNN模型和Vgg16模型在识别噪声数据时，波形的高权值部分较多。而ResNet18模型和Inception10模型所依赖的波形特征较少。

4 结论

本文使用CNN模型、ResNet18模型、Inception模型和Vgg16模型对地震和爆破事件波形進行分类，并通过Grad-CAM算法对4种深度学习模型的可解释性进行了分析。

在福建地区的地震事件分类应用中，4种模型的测试集分类准确率均在96%以上。其中CNN模型和Inception10模型的准确率分别为98.68%和97.55%。ResNet18模型的准确率为96.71%，在4种模型中最低。Vgg16模型的准确率最高，达到99.07%。4种模型在地震事件的分类任务中准确率均比较高，而且具有较好的泛化能力。通过对模型的可解释性分析可以看出，Vgg16模型和CNN模型能够比较准确地注意到波形中P波和S波的震相特征，对于地震波到达之前和能量衰减的位置依赖性较小，而ResNet18模型和Inception模型做出判决时对于整条波形的依赖比较广泛，不能很好地注意到地震波的震相特征。因此，由模型的可解释性分析也可以预测出Vgg16和CNN模型的分类效果应该好于其他2种模型，而实际的分类结果确实如此。

本文通过为每个模型加入Grad-CAM算法，使得模型的黑盒问题得到解决，提高了研究人员对于深度学习网络的信任度，能够让研究人员了解到模型做出判决时对于波形的依赖，从而能够选择更合适的模型并且去修改模型。对于地震事件分类任务来说，波形数据比较小，CNN模型结构简单，分类精度高，训练耗时少，更适合应用于地震事件分类任务中。由于CNN模型和Vgg16模型对于P波和S波初至较为敏感，也可尝试将这2种模型应用到P波和S波到时拾取的研究中。

致谢：福建省地震局林彬华高级工程师提供的地震波形资料，美国劳伦斯利弗莫尔国家实验室Kong教授提供的神经网络可视化代码，以及python开源编程平台，在此一并表示感谢。附所用深度学习模型及可视化程序代码链接：https：//github.com/Luxiaochen2022/Grad-CAM.git。

参考文献（References）

［1］ 边银菊.Fisher方法在震级比mb/MS判据识别爆炸中的应用研究［J］.地震学报，2005，27（4）：414-422.

BIAN Yinju.Application of Fisher method to discriminating earthquakes and explosions using criterion mb/MS［J］.Acta Seismologica Sinica，2005，27（4）：414-422.

［2］ 杨芳，朱嘉健，刘智，等.广东地区地震与爆破事件识别方法研究［J］.华南地震，2016，36（3）：110-115.

YANG Fang，ZHU Jiajian，LIU Zhi，et al.Study on identification methods between earthquakes and explosions occurred in Guangdong region［J］.South China Journal of Seismology，2016，36（3）：110-115.

［3］ 蔡杏辉，邵平荣，段刚，等.福建地区人工爆破与天然地震的判定［J］.地震地磁观测与研究，2013，34（增刊1）：87-91.

CAI Xinghui，SHAO Pingrong，DUAN Gang，et al.Waveform distinction between artificial explosions and natural earthquakes recorded in Fujian area［J］.Seismological and Geomagnetic Observation and Research，2013，34（Suppl01）：87-91.

［4］ 崔鑫，许力生，许忠淮，等.小地震与人工爆破記录的时频分析［J］.地震工程学报，2016，38（1）：71-78.

CUI Xin，XU Lisheng，XU Zhonghuai，et al.Time-frequency analysis of records of small earthquakes and explosions［J］.China Earthquake Engineering Journal，2016，38（1）：71-78.

［5］ 霍祝青，王俊，张金川，等.江苏地区天然地震与人工爆破识别研究［J］.地震工程学报，2015，37（1）：228-231.

HUO Zhuqing，WANG Jun，ZHANG Jinchuan，et al.Recognition study on earthquakes and explosions in Jiangsu area［J］.China Earthquake Engineering Journal，2015，37（1）：228-231.

［6］ MOUSAVI S M，ELLSWORTH W L，ZHU W Q，et al.Earthquake transformer：an attentive deep-learning model for simultaneous earthquake detection and phase picking［J］.Nature Communications，2020，11：3952.

［7］ 赵明，唐淋，陈石，等.基于深度学习到时拾取自动构建长宁地震前震目录［J］.地球物理学报，2021，64（1）：54-66.

ZHAO Ming，TANG Lin，CHEN Shi，et al.Machine learning based automatic foreshock catalog building for the 2019 MS6.0 Changning，Sichuan earthquake［J］.Chinese Journal of Geophysics，2021，64（1）：54-66.

［8］ 高永国，尹欣欣，李少华.基于深度学习的地震与爆破事件自动识别研究［J］.大地测量与地球动力学，2022，42（4）：426-430.

GAO Yongguo，YIN Xinxin，LI Shaohua.Automatic recognition of earthquake and blasting events based on deep learning［J］.Journal of Geodesy and Geodynamics，2022，42（4）：426-430.

［9］ 化盈盈，张岱墀，葛仕明.深度学习模型可解释性的研究进展［J］.信息安全学报，2020，5（3）：1-12.

HUA Yingying，ZHANG Daichi，GE Shiming.Research progress in the interpretability of deep learning models［J］.Journal of Cyber Security，2020，5（3）：1-12.

［10］ FJELLAND R.Why general artificial intelligence will not be realized［J］.Humanities and Social Sciences Communications，2020，7（1）：1-9.

［11］ KONG Q K，WANG R J，WALTER W R，et al.Combining deep learning with physics based features in explosion-earthquake discrimination［J］.Geophysical Research Letters，2022，49（13）：l098645.

［12］ ZHANG Z Z，XIE Y P，XING F Y，et al.MDNet：a semantically and visually interpretable medical image diagnosis network［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Honolulu，HI，USA：［s.n.］，2017：3549-3557.

［13］ 李玮杰，杨威，刘永祥，等.雷达图像深度学习模型的可解释性研究与探索［J］.中国科学：信息科学，2022，52（6）：1114-1134.

LI Weijie，YANG Wei，LIU Yongxiang，et al.Research and exploration on the interpretability of deep learning model in radar image［J］.Scientia Sinica （Informationis），2022，52（6）：1114-1134.

［14］ HE K M，ZHANG X Y，REN S Q，et al.Deep residual learning for image recognition［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Las Vegas，NV，USA：［s.n.］，2016：770-778.

［15］ SZEGEDY C，LIU W，JIA Y Q，et al.Going deeper with convolutions［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Boston，MA，USA：［s.n.］，2015：1-9.

［16］ SIMONYAN K，ZISSERMAN A.Very deep convolutional networks for large-scale image recognition［EB/OL］.2014：arXiv：1409.1556.https：//arxiv.org/abs/1409.1556.

［17］ 曾春艳，严康，王志锋，等.深度学习模型可解释性研究综述［J］.计算机工程与应用，2021，57（8）：1-9.

ZENG Chunyan，YAN Kang，WANG Zhifeng，et al.Survey of interpretability research on deep learning models［J］.Computer Engineering and Applications，2021，57（8）：1-9.

［18］ HAUFE S，MEINECKE F，GORGEN K，et al.On the interpretation of weight vectors of linear models in multivariate neuroimaging［J］.NeuroImage，2014，87：96-110.

［19］ ERHAN D，BENGIO Y，COURVILLE A，et al.Visualizing higher-layer features of a deep network［R］.Montreal：University of Montreal，2009.

［20］ SUNDARARAJAN M，TALY A，YAN Q Q.Gradients of counterfactuals［EB/OL］.2016：arXiv：1611.02639.https：//arxiv.org/abs/1611.02639.

［21］ ZHOU B L，KHOSLA A，LAPEDRIZA A，et al.Learning deep features for discriminative localization［C］//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Las Vegas，NV，USA：［s.n.］，2016：2921-2929.

［22］ SELVARAJU R R，DAS A，VEDANTAM R，et al.Grad-CAM：why did You say that？［EB/OL］.2016：arXiv：1611.07450.https：//arxiv.org/abs/1611.07450.

［23］ SELVARAJU R R，COGSWELL M，DAS A，et al.Grad-CAM：visual explanations from deep networks via gradient-based localization［C］//Proceedings of the IEEE International Conference on Computer Vision.Venice，Italy：［s.n.］，2017：618-626.

［24］ GOODFELLOW I，BENGIO Y，COURVILLE A.Deep learning［M］.Cambridge，Boston，Massachusetts，USA：The MIT Press，2016.

［25］ KINGMA D P，BA J.Adam：a method for stochastic optimization［EB/OL］.2014：arXiv：1412.6980.https：//arxiv.org/abs/1412.6980.

［26］ 林學楷，许才军.深度学习驱动的地震目录构建：PhaseNet和EqT模型的对比与评估［J］.武汉大学学报（信息科学版），2022，47（6）：855-865.

LIN Xuekai，XU Caijun.Deep-learning-empowered earthquake catalog building：comparison and evaluation of PhaseNet and EqT models［J］.Geomatics and Information Science of Wuhan University，2022，47（6）：855-865.