基于车桥耦合分析与神经网络的桥梁损伤识别

何兴文　王宝　石磊　朱巍志

【摘    要】：开发一种基于车桥耦合振动分析与神经网络技术的桥梁结构损伤识别方法。以车辆行驶引起的振动响应为输入，以结构损伤状态为输出，建立能够实现桥梁损伤识别的神经网络。采用数值仿真模拟，首先设定桥梁可能发生的损伤模式，利用自主研发的车桥耦合分析程序，计算桥梁在假定损伤模式下的车致动力响应；反过来将得到的振动响应作为输入训练数据，假定损伤状态作为输出目标，建立神经网络从而实现桥梁的结构损伤识别。使用简支梁桥和平面车辆模型阐述所提出方法的基本理论并进行可行性评估。

【关键词】：桥梁；损伤识别；车桥耦合；神经网络；机器学习

【中图分类号】：U441.4【文献标志码】：A【文章编号】：1008-3197（2023）01-20-04

【DOI编码】：10.3969/j.issn.1008-3197.2023.01.006

Bridge Damage Identification Based on Vehicle Bridge Coupling Analysis

and Neural Network

HE Xingwen1， WANG Bao1， SHI Lei2*， ZHU Weizhi1

（1. Faculty of Infrastructure Engineering， Dalian University of Technology， Dalian 116024， China；

2. Civil Architecture Design and Research Institute Co. Ltd， Dalian University of Technology，Dalian 116024， China）

【Abstract】：The paper developes a bridge structure damage identification method based on vehicle bridge coupling vibration analysis and neural network technology. With the vibration response caused by vehicle driving as the input and the structural damage state as the output， a neural network that can realize bridge damage identification is established. Using numerical simulation， the paper firstly sets the possible damage mode of the bridge and calculates the vehicle induced dynamic response of the bridge under the assumed damage mode using the self-developed vehicle bridge coupling analysis program. In turn， the obtained vibration response is taken as the input training data， and the damage state is assumed as the output target. Then， a neural network is established to realize the structural damage identification of the bridge. The paper uses simple supported beam bridge and a plane vehicle model to illustrate the basic theory of the proposed method and evaluate its feasibility

【Key words】：bridges； damage identification； vehicle bridge coupling； neural network； machine learning

利用健康监测结果对结构进行有效损伤识别，是桥梁健康状态评估的首要任务。桥梁工作者尝试应用各种方法对桥梁结构进行损伤识别，包括静力测试、动力模型参数、智能计算等结构评估方法[1]。对常时微动不明显的中小型桥梁，如果能够确保精度，桥梁车致振动响应进行结构损伤识别是一种高效且实用的方法[2]；其设置传感器较为方便，能够在不中断交通的条件下快速地获得桥梁结构的损伤情况，具有广阔的应用前景。

本文基于Hattori H等[3]提出的方法及自主研发的车桥耦合振动分析与神经网络程序，利用平面汽车荷载下的简支梁桥对提出的损伤识别方法进行可行性研究。首先假定桥梁可能产生的结构损伤模式，使用自编的车桥耦合振动计算程序，模拟每个损伤模式下桥梁结构产生的振动响应；将上述振动响应作为输入训练数据，取一部分作为学习样本，假定损伤模式作为目标输出数据，建立桥梁损伤识别神经网络；然后取其余未学习部分结构损伤模式作为测试样本，验证用已建立的神经网络算法识别桥梁结构损伤模式是否有效。通过与事先设定的损伤模式进行对比，如能达到要求的识别精度，则可以确认利用该神经网络进行桥梁結构损伤识别的可行性。

1 车桥耦合振动响应分析

1.1 车辆模型及公式化

利用平面简支梁桥模型和二自由度车辆模型，阐述所提方法的基本理论及进行可行性评估。将车辆模拟为二自由度（只考虑车身沉浮自由度zj与点头自由度θj）的振动系统[4] 。见图1和见表1。

设定车轮与桥面接触点共有位移来实现车桥耦合并考虑路面不平顺的影响。

车体的沉浮运动方程

[mjzj+l=1lx（j）vjl（t）=0] （1）

车体的点头运动方程

[Ijθj+l=1lx（j）（-1）lλjlvjl（t）=0] （2）

[vjl（t）=kjlzj+（-1）lljlqj-1kx（l）k=1kx（l）wjlk+           cjlzj+（-1）lljlqj-1kx（l）k=1kx（l）wjlk] （3）

式中：j为汽车序号；l=1、l=2为该车的前、后悬挂装置；k=1、k=2为悬挂装置的前、后车轴；vjl（t） 为由弹簧伸缩和阻尼引起的作用力；wjlk为车轮位移，由车轮接触点处桥梁结构变形产生的挠度w（t，xjlk）及路面不平顺z0（xjlk）组成。

[wjlk=w（t，xjlk）+z0（xjlk）] （4）

式中：[wt，xjlk=ΨTjlktwb]，wb为桥梁模型节点位移向量；[Ψjlkt=0;……;0;ψn，jlk;ψn+1，jlk;0;……;0T]，代表单元两端节点位移转换成实际接触点位移的分配向量。

车辆轮载

[Pjlk（t）=-1kx（l）g（1-λjlλj）mj+mjl+1kx（l）vjl（t）] （5）

以矩阵形式表示车辆的运动微分方程

[Mvwv+Cvwv+Kvwv=Fv] （6）

式中：Mv、Cv、Kv、Fv分别为车辆模型的质量、阻尼、刚度矩阵，外力向量；wv为车辆模型全部自由度构成的位移向量。

1.2 桥梁模型

采用有限元法建立平面简支梁桥的梁单元模型。见图2。

桥梁跨度为50 m，等间距划分为25个单元，材料的弹性模量为3.38×1010 N/m2，剪切模量为1.35×1010 N/m2，抗弯惯性矩为15.353 m4，单位长度质量为32.84 t/m。

基于有限元及结构振动理论，桥梁的运动方程可表示为

[Mbwb+Cbwb+Kbwb=Fb] （7）

式中：Mb、Cb、Kb、Fb为桥梁模型的质量、阻尼、刚度矩阵、外力向量。

本文采用Rayleigh阻尼获取桥梁结构阻尼矩阵。

[Mb=i=1nφiqi=Φ?q] （8）

式中：wb为桥梁模型节点位移向量，可用特征向量φi及节点广义坐标qi表示。[q=q1q2…qnT]为振型叠加法中的广义坐标；Φ为桥梁结构的振型矩阵。

根据振型叠加法理论，桥梁结构的振动方程最终可简化为相互独立的非联立形式的方程组

[Miqi+Ciqi+Kiqi=Fi] （9）

式中：Mi为全系统的等效质量矩阵；Ci为等效阻尼矩阵；Ki为等效刚度矩阵；Fi为等效外力向量。

通过轮对与桥梁接触点的耦合位移建立车辆与桥梁模型振动的相互作用关系，联立可得到车-桥耦合系统的全运动方程。

2 基于BP神经网络算法的结构损伤识别

BP神经网络是一种单向传播并且含有多个神经元的网络[5]，是一种从输入层到输出层的高度非线性映射网络，常用的函数为logsig和tansig函数。其网络结构主要由源节点输入层、神经元隐含层及神经元输出层构成。同层神经元隐含层之间没有相关联系，当输入信号从源节点输入层输入后，通过各层神经元隐含层，经函数映射关系计算后，输出到神经元输出层，最后得到结果，每一层节点的输出只受上一层节点的影响[6]。见图3。

基于车桥耦合分析与BP算法的损伤识别步骤：

1）使用Fortran语言编制的车桥耦合分析程序计算桥梁在不同损伤状态下的加速度响应；

2）进行BP神经网络输入输出向量的计算，结构在不同损伤情况下桥梁加速度作为输入向量，桥梁损伤的位置与程度作为输出向量；

3）设计BP神经网络，对神经网络进行训练，将学习样本提取出并用BP神经网络建立加速度与结构损伤的非线性映射关系，达到允许的计算误差后结束训练；

4）测试神经网络，将测试样本输入到BP神经网络中进行测试，验证网络结构对损伤的识别效果。

3 简支梁结构损伤识别效果分析

通过改变单元抗弯刚度来模拟结构损伤，如果单元没有损伤，则输出为1.0；如果单元刚度损伤30%（70%保留），则输出值为0.7。设定损伤程度10%～70%，步长10%，有7种损伤程度。实际结构损伤过大时结构响应可为非线性，本文仅为验证提出方法的可行性，假设结构在大损伤状态下仍保持弹性变形。每种工况的输入数据为简支梁桥模型26个节点的5 s加速度响应，每个节点的加速度响应间隔为0.005 s，共999个数据；输出为25个单元的损伤状态。设定输入向量为26×999矩阵，输出向量为1×25矩阵；神经网络为3层， 输入层的神经元为25 974个，输出层的神经元为25个，隐藏层的神经元为850个。学习过程中的拟合误差设定为10-8。

3.1 单损伤识别效果

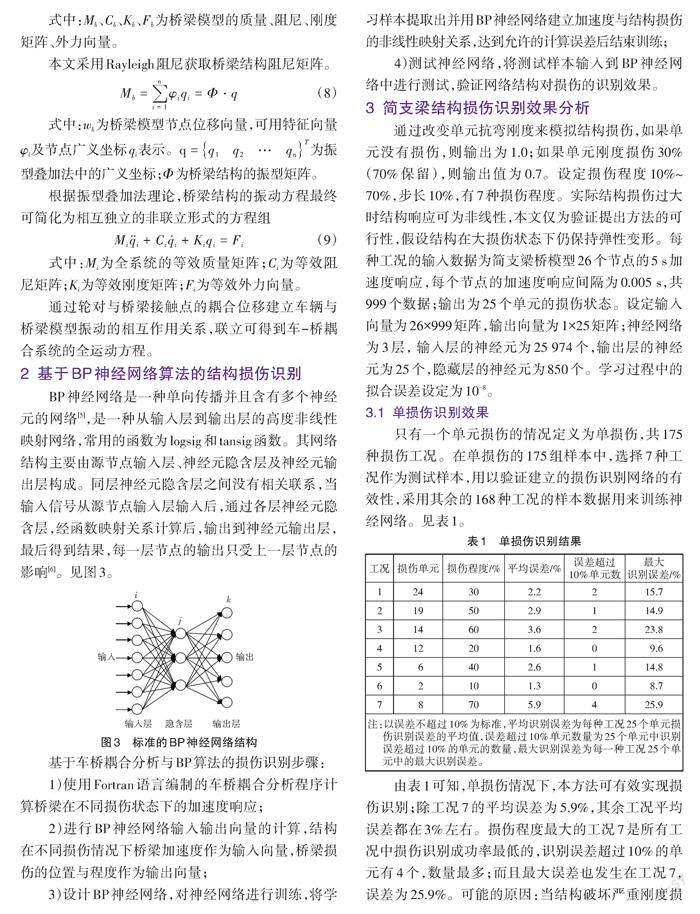
只有一个单元损伤的情况定义为单损伤，共175种损伤工况。在单损伤的175组样本中，选择7种工况作为测试样本，用以验证建立的损伤识别网络的有效性，采用其余的168种工况的样本数据用来训练神经网络。见表1。

由表1可知，单损伤情况下，本方法可有效实现损伤识别；除工况7的平均误差为5.9%，其余工况平均误差都在3%左右。損伤程度最大的工况7是所有工况中损伤识别成功率最低的，识别误差超过10%的单元有4个，数量最多；而且最大误差也发生在工况7，误差为25.9%。可能的原因：当结构破坏严重刚度损失过大时，桥梁的加速度响应发生了较大变化，与中轻度损伤发生时的加速度响应的规律不同，导致神经网络得到的映射不适合辨识损伤程度较大的加速度响应。

其他原因还可能：一是由于网络训练的输入样本数量不够，没有满足神经网络基本要求，所以识别精度不高；二是由于BP神经网络的算法趋于保守，影响预测结果精度。为了提高神经网络的预测准确度，需要将样本容量扩大，再进行神经网络学习。

3.2 双损伤识别效果

有两个单元同时损伤的情况定义为双损伤，利用计算机程序，生成3 000种工况作为样本。双损伤工况下容易擴大学习样本容量，随机选择10种工况作为测试样本，用以验证建立的损伤识别网络的有效性，采用其余2 990种工况样本数据用来训练神经网络。见表2。

双损伤情况下，除工况9的平均误差为4.5%之外，其余工况的平均误差都在2%左右，基本满足损伤识别的要求。双损伤的最大误差16.1%比起单损伤的最大误差25.9%有一定程度降低；而且只有4个工况、共7个单元的损伤识别误差超过了10%。提高学习样本的数量对BP神经网络学习准确度一定积极影响。

3.3 加入噪音的三损伤测试样本数据结果分析

桥梁健康监测的实测数据会包含诸多不确定性，为了测试神经网络抗噪性能，加入噪音函数到加速度响应

[Accumeasured=Accu+σAccu×Ep×Noise] （10）

式中：[Accumeasured]为损伤状态下加入噪音的加速度响应； [σ]为标准差；[Ep]为噪音级别；Noise为满足（0，1）之间标准正态分布的随机向量。

以三损伤识别样本作为对象，将输入的加速度响应代入式（10），噪音级别为5%，得到神经网络损伤识别情况。见表3。

考虑噪音影响后，所有工况的平均误差提高不超过1.9%；说明噪音对损伤识别精度有一定程度的影响，但影响并不大，该方法进行桥梁损伤识别有一定的抗噪性。考虑噪音后，误差超过10%的单元数增加最多的工况几乎都有某一单元发生70%的损伤，说明损伤程度大的结构受噪声影响大。

4 结论

1）基于车桥耦合分析与神经网络的桥梁损伤识别方法用于结构损伤识别具有很高的可行性。

2）提高学习样本容量空间有助于提高损伤识别的精度，本方法对多损伤情况仍然有较高的识别精度。

3）本方法利用桥梁加速度响应进行损伤识别具有较好的稳定性和抗噪性，损伤程度大的情况下结构受噪声影响较大。

参考文献：

[1]贾明晓，连    鑫. 桥梁结构损伤识别方法综述[J]. 科技风，2017，（11）：101-102.

[2]陈上有，夏    禾，战家旺. 基于车桥耦合振动分析的桥梁损伤诊断方法评述[J]. 中国安全科学学报，2007，（8）：148-155+177.

[3]Hattori H ， He X ， Catbas F ， et al. A bridge damage detection approach using vehicle-bridge interaction analysis and Neural Network technique[C]. Bridge maintenance， safety， management， resilience and Sustainability[A].  Proceedings of the sixth international conference on bridge maintenance， safety and management，2012.

[4]刘世忠. 双层公路钢桁梁桥车桥耦合振动研究[D]. 西安：长安大学，2015.

[5]周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2005.

[6]田景文，高美娟.人工神经网络算法研究及应用[M].北京：北京理工大学出版社，2006.

收稿日期：2022-06-09

作者简介：何兴文（1975 - ）， 男， 博士， 辽宁海城人， 教授， 研究方向为桥梁工程、结构动力学。

通讯作者：石磊（1975 - ）， 男， 博士， 辽宁营口人， 高级工程师， 从事桥梁设计工作， Email：shi_lei@dlut.edu.cn。