基于小波变换的小电流接地选线研究

魏圣泰，翁玉翔

（1.国网江苏省供电公司靖江供电分公司，江苏 靖江 214500；2.国网江苏省供电公司泰州供电分公司，江苏 泰州 225300）

小电流接地故障是电力系统中常见的一种故障形式，其原因多种多样，包括设备故障、雷击、地质等原因。为了有效诊断和排除小电流接地故障，需要对接地电流进行监测，选择合适的接地线路，以实现系统的安全运行。

传统的小电流接地监测方法主要是基于电流变压器或电阻器的直接观测，监测精度较低，并且需要分时段检测以保证监测准确性，操作繁琐；而基于小波变换的小电流接地选线分析技术则可以有效解决这些问题。小波变换是一种数学工具，具有时频分析的优势，可以将时间信号分解成不同时频域的小波分量。在小电流接地监测中，可以使用小波变换对接地电流信号进行分解和重构，以获得更具代表性的信号。同时，由于小波变换可以对信号进行跟踪和提取，故可以有效地检测出小电流接地故障信号，并进行有效的诊断和预测。在小电流接地选线分析中，可以使用小波变换提取不同频率段的接地电流信号，以判断接地点的位置和类型，并选取合适的接地线路。此外，由于小波变换能够实现精确的信号处理，能够有效地降低检测误报率，提高监测准确性。

基于小波变换的小电流接地选线分析技术是一种有效的监测方法，可以提高小电流接地故障监测的准确性和效率，具有重要的应用价值。

1 技术分析

小电流接地系统（SCGS）广泛应用于66kV及较低电压水平的配电网中，单相接地故障数超过配电网总故障数的80%。电力系统中，小电流单相接地故障的检测受到故障状态复杂性的限制，如故障特征小、持续时间短、对整个系统影响小等，需要在配电系统中尽快准确地选择单相接地故障线路［1-2］。行波法利用配电线路远端反射的行波与断层之间的差异，在这种方法中，断层产生的行波可能受到天线元件、电容器和电感器以及谐波的幅值和振幅的影响。利用这些因素可以准确地选择故障线路，但要捕捉到详细的行波，需要较高的采样率，这意味着硬件设备和整个保护系统的成本可能会增加。单相接地结构示意图如图1所示。

图1 单相接地结构示意图

如果变电站变压器绕组一侧的中性点接地不当，则绕组、母线和与该母线连接的线路形成SCGS。因此，当小电流接地系统发生单相接地故障时，故障线路中不能检测到明显的故障特征，从多条接地线路中选择故障线路称为故障选线（FLS）问题［3-4］。由于断层具有随机过程和不明显的断层特征，FLS会比较复杂。

传统的FLS方法可分为稳态法、瞬态法和注入法。由于稳态信号通常很弱、容易受到干扰、稳态方法精度较低、难以在实际中应用［5］。暂态信号幅值大，但暂态过程持续时间短，具有一定的随机性，在一定情况下容易产生误判。由于稳态法，瞬态法的理论瓶颈，很难充分考虑具有一定随机性的单相接地故障过程。因此，它们的FLS精度一般低于70%。为了提高故障选线的准确性，有学者提出利用神经网络等数据驱动方法从历史数据中学习故障特征，并利用这些特征选择故障选线。这种方法需要大量的故障样本，在小样本情况下模型的训练非常不稳定，FLS精度不够高。

本文在传统研究基础之上，提出了小包变换方式的小电流接地故障选线。首先，引入小波包分解对2个周期的瞬态零序电流进行分解，去除最低频带［4 0］后，得到所选频带［4 1］、［4 2］；其次，根据隶属函数，对得到的值进行归一化后，得到故障隶属值;最后，如果最大隶属度值与第二个最大隶属度值之差大于或等于设定的阈值，则选择最大隶属度值对应的线路作为故障线，否则判断母线为故障线。

2 理论分析

2.1 小波变换及信号距离

小波包变换能够准确地分解信号的高频部分，在分解过程中不需要提出冗余信号或遗漏信号，因此适合于对含有大量中高频信号的信息进行时频局部化分析。本文将小波包变换理论应用于故障选线。小波包变换的基本理论如下。定义函数由方程（1）给出:

其中n＝0，1，2，…是由正交尺度函数u0＝f定义的小波包。小波包提供了一种更为复杂的分析方法，可以对高频部分进行连续分解。因此，可以通过识别单相接地信号的特征来选择相应的频带进行分析。

为了表示两个故障信号之间的差异，最简单的方法是在相应的时间比较这些信号，并计算比较范围内差异的平均值。如果x（n）和y（n）分别是随机遍历信号X（n）和Y（n）的两个采样函数，而y（n＋m）是y（n）的时移信号序列。信号相互距离函数可定义为下式：

其中，△xy（m）表示信号x（n）和信号y（n＋m）之间的差异程度，其对应点在这些信号函数中的值，即x（n）和y（n＋m）称为信号距离。

信号距离空间中每两个元素之间的距离矩阵称为信号距离矩阵，如公式（3），其中△ij 表示信号i和信号j之间的信号距离。

信号距离矩阵是一个正方形矩阵，其中主对角线上的元素表示信号与其自身之间的距离。对于时域有限的因果信号，根据信号距离的概念，主对角线上的元素为0，矩阵称为主对角线上的对称方阵，如式（4）所示。

在暂态过渡阶段，故障支路的零序电流幅值大于非故障支路，且极性相反，而且故障支路的零序电流变化速率与非故障支路的零序电流变化速率也有显著差异。因此，利用这些特性，可以在故障选线中使用信号距离策略。

2.2 选线程序

本文利用多分辨率小波包的优点，采用db4小波包对故障时的零序电流进行了分析。对单相接地故障的零序电流进行多层小波包分解，并将结果分布在每个频率。对单相接地故障的零序电流进行多层小波包分解，并将结果分布在从低频到高频的每个频带。将所有m个支路的零序电流分解成适当的频率，各频段的系数，其中表示分解系数（j，k）；m为电力系统中支路的个数；n为各频段的系数数；j是小波分解的层数；k是小波分解中的节点。以第一个分支为例，小波包分解得到的系数矩阵，如式（5）所示。

为了最大限度地减少工频50Hz的干扰，本文排除了低频段的系数。

2.3 系数矩阵

本文采用信号距离函数对零序电流系数进行处理，以选择故障线路。一个信号距离矩阵S，如下式（7）所示。

其中，amm是分支中每个节点的之和。

信号距离矩阵是一个方阵，其中的主要对角元素表示信号与其自身之间的距离; 因此，对于时域因果信号，主要对角元素保持为0，如式（8）所示。

通过加入信号距离矩阵每行的元素，得到式（9）中所示的故障选线向量D。

线路选择矢量表示为D＝［D1，D2，…Dm］，其中故障线路可以通过D1，D2，…Dm的最大值来选择。

3 实验分析

本文建立相应的仿真模型，其结构模型如图2所示。

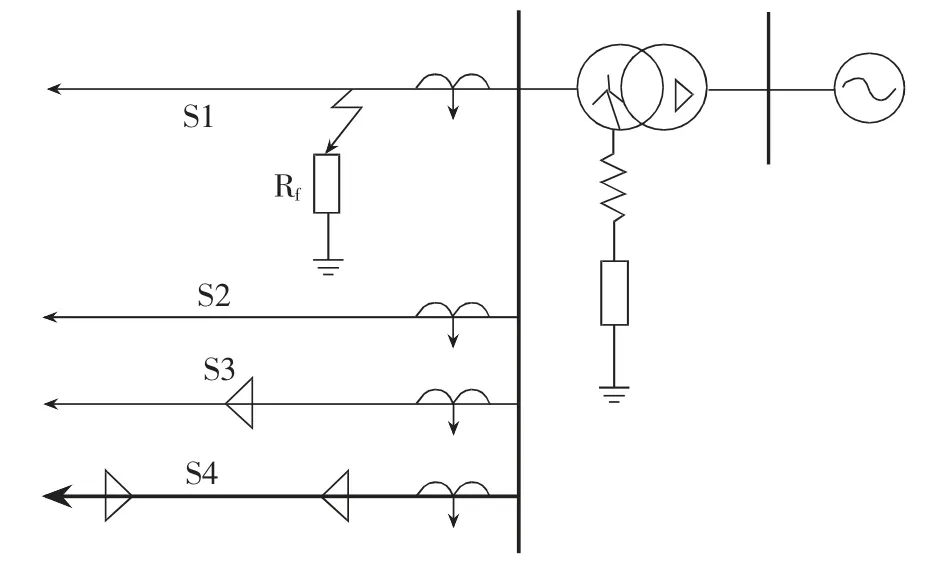
图2 结构模型

中性点消弧线圈故障仿真单相接地故障发生时，采样频率为105Hz，总仿真时间为0.04s，故障相位为B，初始角度θ=0°，故障电阻R=10Ω。TZSC在前2个周期的波形如图3所示。

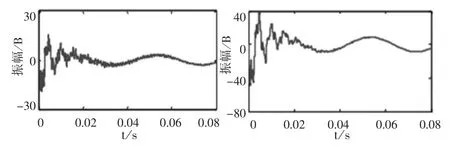
图3 TZSC在前两个周期的波形

从图3可以看出，故障发生时，TZSC信号变化迅速，波形逐渐衰减。经db10小波函数分解4层后，去掉最低频段［4 0］，选取频带［4 1］、［4 2］作为所选频带。由于空间原因，选取故障线2为例，得到的特征频带如图4所示。

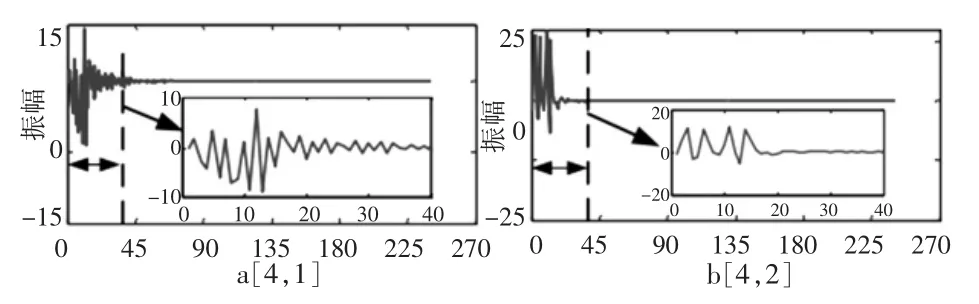
图4 线路2特征频带

根据以上选取的波段，形成仿真图，如图5所示。

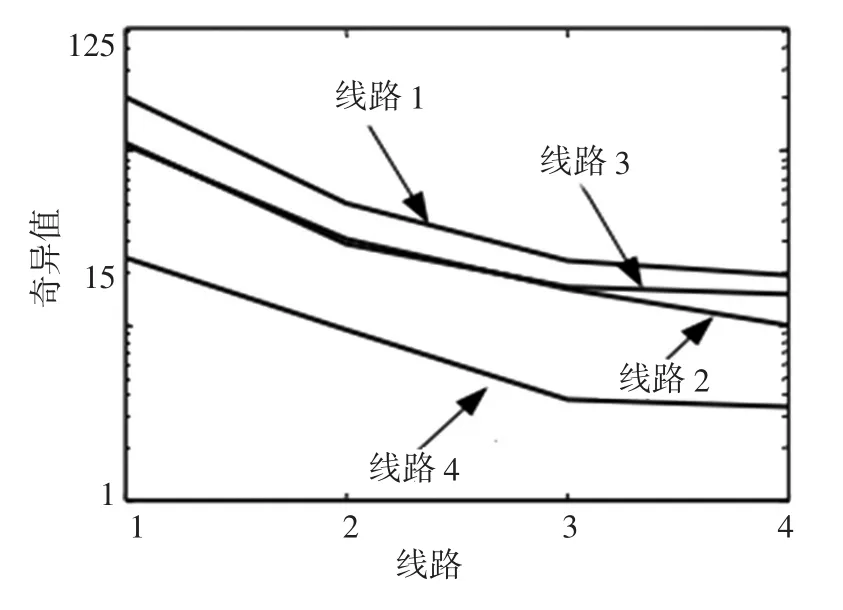
图5 各线路变换值仿真图

为验证本文所提出方法的适用性，分别改变故障线路类型、故障电阻、故障初始相角，结果分别如表1、表2、表3所示。最后，将不同的高斯白噪声单次注入到TZSC中，结果如表4所示。

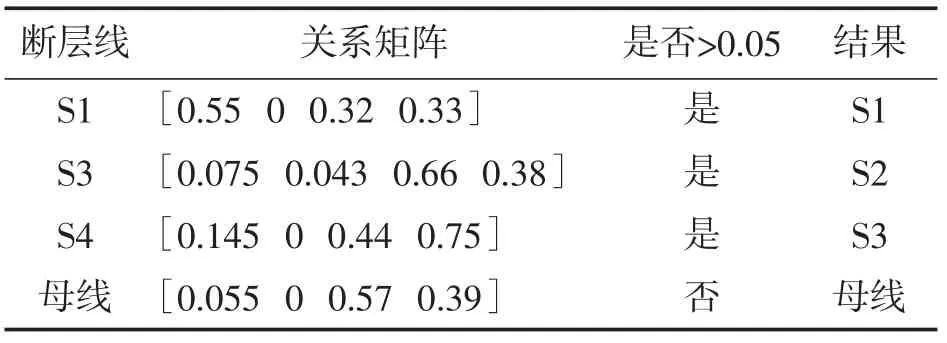
表1 改变故障线路类型

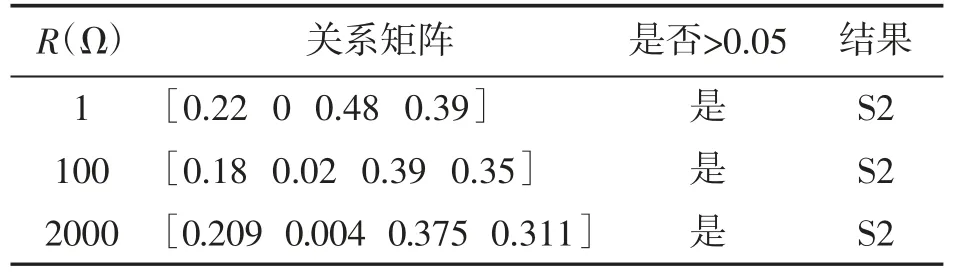
表2 改变故障电阻

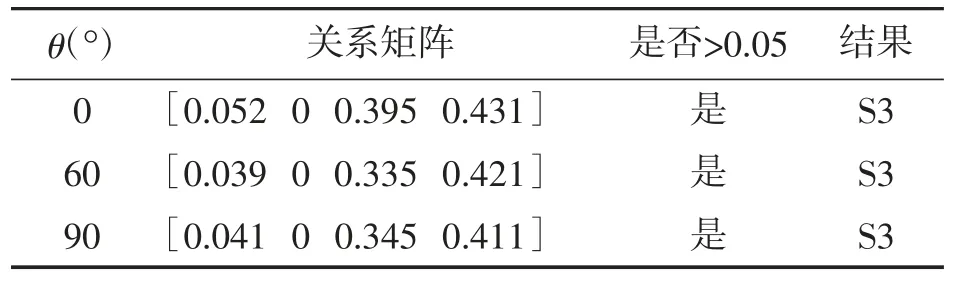
表3 改变故障初相角

表4 改变故障初相角

a）不同的断层线类型

当分别发生架空线路、电缆线路故障和混合线路故障时，故障初始相位角为0°，故障电阻为100Ω，基于所提出方法的选择结果如表1所示。选择结果表明，所提出的选择方法可以在故障线路类型变化时选择故障线路的精度。

b）不同的故障电阻

当混合线S3故障发生时，故障电阻不同，初始故障初始相位角为0°时，基于所提方法的选择结果如表2所示。选择结果表明，本文提出的方法可以准确地选择故障线路。

c）不同的故障初始相角当电缆线路S4故障发生时，故障初始相角不同，初始故障电阻为100°时，基于所提方法的选择结果如表3所示。选择结果表明，本文提出的方法可以选择故障线路的精度。

d）不同的噪音

在TZSC中注入不同的高斯白噪声，信噪比（SNR）分别为20dB、-5 dB和-10 dB，当故障初始相位角为0°，故障电阻为100Ω时，选择结果见表4所示。可以看出，当SNR很大时，选择结果仍然正确。因此，本文所提出的方法具有较强的抗噪声能力。

4 结论

本文提出了一种基于小波变换的小电流接地自适应故障选线方法。当故障发生时，采用小波包分解的方法，将TZSC信号分解成多个频段，变换值可以反映所选频带中包含的固有故障信息，综合变换值可以描述TZSC中包含的故障特征信息。通过隶属度值对故障严重程度进行量化，并引入阈值来区分故障支路和故障母线，根据差值可以准确选择故障支路，选择结果正确。大量仿真结果表明，本文提出的基于小波变换的小电流接地系统选线方法具有较高的精度、可信度和适应性。