一种抱弹机构非线性静力学分析与结构优化
陈 亮, 张 超, 高 博, 邱群先
(中国船舶集团有限公司第七一三研究所, 河南 郑州 450015)
0 引言
火炮系统中的供输弹系统的主要作用是将外部弹药通过一系列动作将其转运至发射炮膛内,节省人力,保证一定的发射率,是火炮系统中重要的组成部分[1]。 一种车载炮供输弹系统主要有弹鼓和输弹机组成, 弹鼓中可存储一定数量的弹药, 并可以将需要发射的弹药转运至输弹起始位置, 通过输弹机将弹药快速输送至炮膛发射起始位。发射时供弹系统同身管一起实现后坐复进动作,在此过程中存储在弹鼓中的弹药受到后坐冲击的作用,在弹鼓中前后蹿动, 同其他部位发生碰撞, 出现不安全因素,故需要一种抱弹机构对弹药进行约束定位,在输弹时机构打开,保证输弹的顺利进行。故抱弹机构不仅要达到运动灵活,锁弹效果好,亦需要满足抗冲击,有一定的强度和刚度的要求。 同时为达到较高的空间储弹率,抱弹机构的结构尺寸必须满足空间布局的要求。 科研学者对该类似机构进行了许多研究, 中北大学常学芳为研究14.5mm 机枪弹链前后抱弹部建立了枪弹的非线性有限元模型, 用于研究弹链在装弹和脱弹过程中应力以及弹塑性变形规律[2];南京理工大学的顾伟亮针对某火炮系统的自动供输弹机械手基optistruct 平台, 对其抱爪结构采用了拓扑优化, 在满足约束条件下, 降低了机械手的重量,提高了机械手的工作性能[3]。
在一般的静力学分析中,材料满足胡克定律,即为线性静力学分析, 其刚度矩阵为线性矩阵, 刚度系数为常数,在进行迭代计算时,为无条件收敛,但当刚度系数随着材料应变或者应力变化不再保持常数时, 材料表现为非线性结构变化, 引起结构非线性的原因主要体现在几何非线性、材料非线性和接触非线性[4]。 针对抱弹机构的抗冲击设计,为满足刚强度要求,常常表现为材料非线性问题和接触非线性问题。 在进行仿真计算时需要将材料的非线性特征考虑在内更加符合实际应用情况。 在该方面的研究有中国工程物理研究院的尹益辉通过静力学加载实验研究了楔环连接结构试件的非线性静力学行为[5];国防科技大学的郭欣针对运载火箭的刚性包扎带式连接装置建立了预紧状态下的刚性包带及端框结构非线性静力学模型,分析其在轴向承载时的受力特性,并结合轴对称等效和参数化建模技术, 通过优化截面形状参数提升对整体连接性能[6]。
文章针对一种具体的抱弹机构, 采用试验和仿真结合的方法分析,结合变形量,仿真计算非线性静力学状态下的等效作用力,将该力作为输入性条件,为优化优化后的抱弹机构进行校核计算。
1 抱弹机构非线性静力学模型
1.1 抱弹机构结构与工作原理
抱弹机构安装在弹鼓中,其主要由机壳、止簧、锁芯、直拉杆、推块、压簧、左抱弹爪、右抱弹爪、中心推杆组成,所有零件安装在机壳上,并可在内部来回滑动,如图1 所示。 初始状态下左抱弹爪和右抱弹爪在弹簧的作用下向中心移动,抱弹爪卡进弹体凹槽中,将弹丸锁住,防止弹丸前后移动,需要进行输弹时,推块被外力驱动通过与斜面配合,推动左右抱弹爪向两侧移动,使弹丸解锁。 整个工作过程中左右抱弹爪不仅具有左右移动的功能, 同时需要有抵抗弹丸惯性力的能力。

图1 抱弹机构结构图Fig.1 Structure chart of holding play mechanism
1.2 接触非线性静力学分析方法
接触非线性问题通常采用迭代法进行求解, 广泛应用于有限元及其衍生数值分析方法关于静力学接触问题的求解。 在1970 年,Wilson 和Parsons 提出一种求解接触问题[7],该思路基本如下:对两个弹性接触物体,将其进行有限元离散,其有限元方程可写成:
式中:[K]—某种接触状态下的刚度矩阵;{U}—节点位移矢量;{P}—对应的载荷矢量。 对上述关系式进行变换得到:
在求解节点位移{U1}后,即可求解接触节点的接触内应力, 之后将两者带入接触状态条件中, 若不满足条件,修改接触状态,进行下一次迭代计算,不断循环下去,直至{Un}和接触内应力满足接触条件。 以上分析方法在workbench 分析软件中进行了充分应用,其具体计算非线性过如下[8]:系统总位能构造的泛函,通过最小位能原理,推导得到结构有限元方程如式(1)。 基于约束变分原理,采用拉格朗日乘子法、 罚函数法等方法, 引入边界条件(附加条件)C(u)=0,从而构造修正泛函。经多次迭代计算后,找到一稳定的接触状态不一定为真实接触状态,采用Newton-Raphson 方法,检验残差(外载荷与内载荷之差),判别收敛性以达到仿真求解精度,或者采用增广拉格朗日乘子法引入附加条件, 以应对接触区域内的位移穿透进行收敛性判别,并通过调整接触力去迭代。 计算过程如图2 所示。

图2 非线性仿真计算流程图Fig.2 Calculation flow chart of nonlinear simulation
1.3 抱弹爪受力分析与试验
如图3 所示,在后坐过程中,弹丸同抱弹机构一起实现后坐复进运动,对于弹丸而言,其加速运动所需要的力由与其接触的左右抱弹爪提供,由牛顿第三定律可知,左右抱弹爪受到弹丸提供的反作用力,该位置接触面积小,作用应力大,有可能使抱弹爪出现塑性应变,出现变形情况。故主要分析对象为其中的左右抱弹爪零件,由于为对称结构,受力作用相同,取左抱弹爪进行受力分析。 如图3 所示,左抱弹爪受到:

图3 受力分析Fig.3 Force analysis
(1)重力G;
(2)弹丸对其作用力F;
(3)外壳的上下面给予的支撑作用力Fh;
(4)外壳左右面给予的作用力,该左右面有两处,作用力为Fn。
其中(1)和(2)为主动力,(2)和(3)为受到(1)(4)作用产生的响应载荷。 在四个力中主要研究(2)对抱弹爪的的作用效果将力F 左等效平移, 会得到等效作用力F, 和力矩N,该力F, 会使抱弹爪产生弯曲趋势, 同时力矩N 会使其产生扭转趋势,如图4 所示。

图4 作用力F 等效作用Fig.4 Equivalent action of force F
在某次射击试验时,试验次数为5 次,每次试验对其中一弹位装入同等质量的配重弹对抱弹机构中抱弹爪进行抗冲击测试(每组抱弹爪均通过检验测试,符合图纸设计要求), 试验过程中对后坐加速度进行测量,试验完成后发现5 组抱弹爪均出现不同程度的塑性变形,取其中一组变形量最大的抱弹爪进行变形量测量, 测量结果如图5 所示,最大变形量为2.39mm。

图5 最大变形量Fig.5 Maximum deformation
1.4 非线性静力学仿真受力分析
金属零件在受到作用力出现塑性变形,根据应力应变曲线可知,为单调函数,即某个应变值对应唯一一个应力值[9],为计算出在该塑性变形状态下对应的等效作用力,以此为输入边界条件对后续抱弹爪进行结构优化, 对目前该结构状态下的抱弹机构进行模型简化, 同时考虑到实际工况下左右抱弹爪呈对称布置,受力状态相同,为减小计算量,加快计算时间,选择单侧左抱弹爪主体进行分析,保留部分外壳,建立简化后的仿真模型,并对其进行结构化网格进行划分,如图6 所示。

图6 计算模型Fig.6 Calculation model
利用workbench 进行仿真分析[10],在具体设置时为保证塑性变形条件下需要对其进行更改设置, 左抱弹爪和外壳材料选择非线性no-linear materials 中结构钢材料structural steel NL,并根据实际使用的材料相关参数对structural steel NL 的材料数据进行重新设置。
在具体计算仿真设置时, 对抱弹爪和外壳两者的接触面设置为Frictional 连接,摩擦系数取0.2,网格划分时采用六面体网格,为增加计算精度最小网格大小控制在1mm以内。 对Analysis Setting 中对Weak Springs 开启Program Controlled 以减小抱弹爪可能出现横向刚体位移时导致的不易收敛情况。 同时开启Large Deflection 以考虑大变形和大应变引起的单元形状和方向的改变时, 增加计算结果的准确性。 经过不断的尝试计算得到在塑性变形约2.4mm 的情况下, 对应的等效作用力为3512N,如图7 所示左抱弹爪的应力应变云图。

图7 应力应变云图Fig.7 Stress-strain cloud map
该仿真计算显示抱弹爪的变形趋势同实物抱弹爪变形保持了较好的一致性, 最大应力出现在抱弹爪中间的悬臂梁位置处,为629MPa 超过了45 号钢(调质状态下)的屈服强度极限,说明抱弹爪出现出了非线性表现。
2 抱弹爪结构优化设计
2.1 结构参数设计优化
根据1.3 节受力分析和1.4 节的仿真分析中可以看出抱弹爪中间悬置梁出现了弯曲扭转形变, 为需要重点加强的部位,以增加抗弯和抗扭的能力。 但受到本身结构尺寸、重量、总体位置结构限制,悬置量尺寸不可能无限制加强, 需要在约束条件内建立约束方程,进行优化设计。
抱弹爪结构复杂,尺寸约束众多,在进行参数优化时,考虑了主要问题与之相关的悬臂梁和抱爪位置尺寸,如图8 所示的7 个参数,建立条件约束关系式:

图8 抱弹爪结构尺寸Fig.8 Structure size of holding play mechanism
关系式中R 为弹丸的圆柱部直径,H 为弹丸沟槽深度,两者均为常数,M 为抱弹爪优化部分的质量。 以上7个变量参数为优化变量,在满足抱弹爪不发生塑性变形,同时1.2 倍最大应力不大于45 号钢屈服强度的条件下,以质量为最小为优化目标,优化的目标函数表达式为:
采用Matlab 编制计算程序进行计算, 在具体计算过程中,调用多岛遗传算法(MIGA)程序包进行寻优[11],之后对每一组符合条件的解进行参数化建模, 并对每个参数模型进行应力应变的校核,为此需要利用Creo 进行参数建模[12]和Ansys 进行数值仿真计算,通过不断的循环比较计算寻找最优解,在此过程中的数据传递需要用到Isight优化分析软件将各个平台进行搭建[13],形成参数优化仿真平台,具体优化流程如图9 所示。
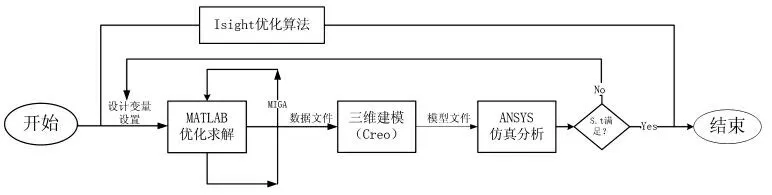
图9 参数化优化流程图Fig.9 Flow chart of parametric optimization
2.2 优化结果分析
经过约200 次轮迭代计算,得出优化过后的参数,考虑到实际工程应用,对相应的数据进行圆整,经再次建模得到优化过后的抱弹爪结构,如图10 所示。
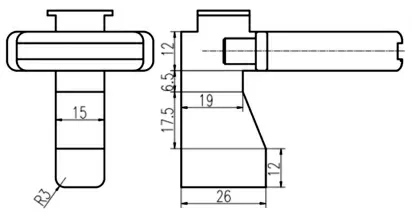
图10 优化后抱弹抓的结构尺寸Fig.10 Structure size of optimized holding play mechanism
从图中可以看出抱弹爪的主要优化位置为悬臂梁位置, 对其进行了加宽加厚处理, 主要数据值均有所增加, 其中悬臂梁的宽度增加值最大,增加量为216.67%,如表1 所示的数据表。 该位置尺寸的显著增加说明能有效增强抱弹爪的抗弯抗扭能力。 对应的质量相对有所增加,增加率为70%,优化后的质量增加界限满足约束条件。

表1 优化前后的参数对比Tab.1 Comparison of parameters before and after optimization
针对优化过后的抱弹爪进行非线性静力学仿真分析,仿真设置同1.4节中所述保持一致, 仿真结果显示抱弹爪最大应力出现在悬臂梁同外壳接触面上沿位置处,最大值为453.3MPa,最大应变出现位置同优化前保持一致, 均在同弹丸接触位置的边缘处, 数值为0.09mm,如图11 所示。 以上数值满足了小于1.2 倍45 号钢(调质后)的屈服极限值的要求,同时变形值亦满足不大于0.2mm 的使用要求。

图11 优化后的应力应变云图Fig.11 Optimized stress-strain cloud map
3 结论
本文针对火炮供输弹系统中的一种具体抱弹机构,采用试验与仿真相结合的方法,建立非线性静力学仿真模型, 并对抱弹机构中的抱弹爪进行结构优化,得出以下结论:
(1)抱弹机构中的抱弹爪在火炮射击后坐冲击过程中受力复杂,难以进行定量分析,通过测试其塑性变形量,反向计算等效作用力可简化分析过程,不改变分析效果。
(2) 采用非线性静力学模型考虑了抱弹爪在塑性变形变形阶段的受力情况,同增加了计算的准确性,但同时也增加了计算量。
(3)Isight 优化分析软件搭建起来的参数化优化平台可大大节省抱弹爪结构优化的计算时间, 同时界面对用户友好度较高,包容性强,可推广应用至其他优化计算场景中。
(4)在材料使用45# 钢材料(调质)的情况下仿真优化结果得到抱弹爪的最大应力应变值均满足使用要求,若更换屈服强度更高的钢材料在满足要求的情况下,可进一步减小抱弹爪的质量。

