角度非均匀连续介质材料反平面V 形切口应力奇性分析

姜 伟,葛仁余,李浚淇,潘家雨,尚 悦

(安徽工程大学 建筑工程学院,安徽 芜湖 241000)

角度非均匀连续介质材料是物理性能参数随着角度坐标连续变化的,这种特殊非均匀介质材料常见于自然界和工程合成材料。长期以来,人们已认识到材料物理性能随着坐标位置变化,既可以增加材料物理性能,又能减少造价成本。为了满足各种特殊工程结构的需要,非均匀连续介质材料也是一种新型合成材料,能将多种物理力学性能各异的材料按照人们的设计意愿,形成材料物理性能连续变化的组织结构。同时,使异质材料结合部位的界面消失,避免了力学性能不连续性和应力集中现象,因此,角度非均匀连续介质材料吸引了广大学者们的研究兴趣[1]。

关于非均匀连续介质材料裂纹和切口的奇异应力场问题,Carpinteri等[2]研究了角度非均匀连续介质材料裂纹的应力奇异性,发现裂纹的应力奇性指数与非均匀材料梯度有关。Cheng等[3]运用插值矩阵法(IMM)计算了角度非均匀连续介质材料平面和反平面切口和裂纹的应力奇性指数,但是,Carpinteri和Cheng没有进一步给出角度非均匀连续介质材料切口和裂纹尖端处的完整奇异应力场。目前,据作者所知,平面楔形体受体积力和集中荷载作用时,仅有Theotokoglou等[4-6]基于线弹性理论研究了角度非均匀连续介质材料的静力问题。Delale等[7]研究了泊松比为常数,杨氏模量为指数函数变化的非均匀材料的平面断裂问题,研究发现:泊松比对裂纹尖端应力强度因子的影响可以忽略不计;同时,Delale等[8]分析了处于均匀材料半平面和非均匀材料半平面之间的界面裂纹问题,研究表明:只要材料的力学属性在裂纹尖端保持连续,非均匀材料与均匀材料裂纹尖端应力场的奇异性是一致的。Konda等[9]研究了材料非均匀常数、裂纹方向、加载条件和泊松比对裂纹的应力强度因子的影响;Gao[10]运用摄动算法研究了非均匀连续介质材料裂纹的断裂力学问题;基于三重互易边界元方法,Ochiai[11]研究了非均匀连续介质材料二维弹性应力场和三维热传导问题。Zhou等[12]运用复变函数方法研究了夹杂物对非均匀介质材料弹性力学解的影响。基于奇异积分方程的方法,Erdogan等[13-14]研究了非均匀连续介质材料平面裂纹问题;运用相互积分法,Yu和Sladek等[15-19]研究了非均匀连续介质材料裂纹问题,Itou等[20]分析了非均匀连续介质材料界面裂纹问题;基于梯度有限元法,Kim 等[21]研究了非均匀连续介质材料的裂纹问题;通过求解柯西型奇异积分方程的方法,Yong等[22]研究了粘结弹性材料的反平面裂纹问题;Wang和Monfared等[23-24]研究了非均匀各向异性材料的动态反平面多裂纹应力奇性问题;基于边界积分方程的方法(BIEM),Zhang等[25]研究了非均匀连续介质材料裂纹的应力奇性问题。

DQM 的基本原理是对于任意连续函数,将其定义域上各点的函数值加权求和来表示各节点处导数值的方法。长期科学研究已证明,该方法求解常微分方程具有公式简单、编程方便、计算量少和精度高等优点,所以在振动工程领域得到了广泛应用,主要用来求解工程结构的自由振动和强迫振动问题。本文将DQM 创新地应用到非均匀连续介质材料断裂力学研究领域,根据弹性力学基本理论,将角度非均匀连续介质材料反平面V 形切口端部应力奇性指数的计算转化为关于应力奇性指数及其相应位移特征函数的常微分方程组特征值问题,由DQM 基本理论,将该常微分方程组的特征值问题转化为标准型广义代数方程组特征值问题,采用正交三角分解(QR)法可一次性地计算出角度非均匀连续介质材料反平面V 形切口和裂纹端部应力奇性指数及其相应的位移特征角函数。

1 角度非均匀材料反平面V 形切口应力奇性分析

切口两边自由的角度非均质材料反平面V 形切口如图1所示,切口张角为α=θ2-θ1,x轴与切口张角的角平分线一致。θ=θ1起始边的弹性模量为E1,θ=θ2终止边的弹性模量为E2,泊松比不随角度变化,取v=0.25。切口内的弹性模量E(θ)按照一定的函数关系变化,如图2所示。

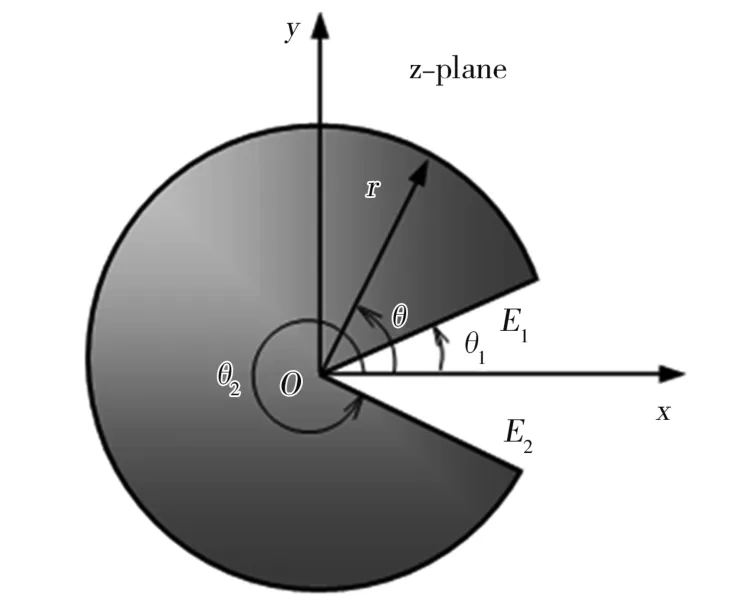
图1 角度非均质反平面切口

图2 材料弹性模量与角度变化的关系

根据线弹性理论,反平面切口尖端区域的渐近位移场w(r,θ)可以表达成极坐标r的渐近展开形式

将式(2)代入反平面问题的应力-应变关系,可以得到应力分量表达式为:

将式(3)代入忽略体积力的弹性力学反平面问题平衡方程

化简得:

为了便于编程计算,引入无量纲变量ξ(0≤ξ≤1),当θ1≤θ≤θ2时,有

将式(7)代入式(6),有

设切口边界θ=θ1和θ=θ2上面的力自由(见图1a),有

将式(3)代入式(9)可以获得如下边界条件:

综上,将角度非均质材料反平面切口奇性分析问题,转化为求解在边界条件式(10)下方程组式(8)的特征值问题。

式中,lj(ξ)为拉格朗日多项式;n为离散单元总数,n+1为离散节点总数,离散节点方式采用具有稳定收敛特性的余弦网格模式,即

由式(11)对函数w~(ξ)求一阶导数,得到:

将式(13)在区间ξ∊[0,1]上离散n段,从而进一步得到:

将式(14)写成向量形式,得:

这里,向量A(1)nn、′和如式(16)所列,

其中,一阶导数的加权系数矩阵A(1)ij显示表达式为:

依次类推可得:

将式(15)、(18)代入式(8),控制方程写成向量形式,化简得:

式中,为变系数对角阵形式,即=diag((ξ0),(ξ1),…,(ξn)),I为(n+1)×(n+1)阶单位矩阵。

以切口两边自由的边界条件为例,写成向量形式为:

这里,Il=0或n。将边界条件式(21)代入控制方程式(20),替换相应的0行或n行,得:

由于式(22)中含有λ2项,导致非线性特征值问题,引入1个新向量g,

其中,g=(g(ξ0),g(ξ1),…,g(ξn-1),g(ξn))T。

联立式(22)和式(23)可得矩阵特征方程组如下:

至此,式(24)为2(n+1)个未知列向量关于应力奇性指数λ的一般广义代数特征方程组。对于广义代数特征值问题,这里采用QR法求解该式,可得到角度非均匀材料反平面V 形切口应力奇性指数λ和相应的特征向量。

2 数值算例

2.1 弹性模量按照角度坐标的指数函数形式变化

假设材料的弹性模量E(θ)按照角度坐标的指数形式变化,且θ=0时的弹性模量为E1,θ=2π时的弹性模量为E2,则

当反平面切口终止边和起始边弹性模量比值E2/E1=1、10、50和100时,取离散单元数n=20,采用DQM计算角度非均匀材料反平面V 形切口尖端区域第1阶应力奇异特征指数值如表1所示。表1计算结果表明:弹性模量按照指数函数形式变化时,采用本文DQM 获得的角度非均匀材料反平面切口应力奇异性指数计算值与文献[3]计算结果完全吻合,证明了本文方法的有效性和精确性。

表1 弹性模量按照角度坐标的指数函数形式变化时反平面切口的奇性指数

2.2 弹性模量按照角度坐标的幂函数形式变化

假设材料的弹性模量E(θ)按照角度坐标的幂函数形式变化,且θ=0°时的弹性模量为E1,θ=2π时的弹性模量为E2,则

当反平面切口终止边和起始边弹性模量比值E2/E1=1、10、50和100时,取离散单元数n=20,采用DQM 计算角度非均匀材料反平面切口尖端区域第1阶应力奇异特征指数值如表2所示。由表2计算结果表明:当角度非均匀材料的弹性模量按照幂函数形式变化时,采用本文DQM 获得的反平面切口应力奇异性指数计算值与文献[3]计算结果完全吻合,再一次证明了本文方法的有效性和精确性。

表2 弹性模量按照角度坐标的幂函数形式变化时反平面切口的奇性指数

2.3 弹性模量按照角度坐标的倒数形式变化

假设材料的弹性模量E(θ)按照角度坐标的倒数形式变化,且θ=0时的弹性模量为E1,θ=2π时的弹性模量为E2,则

当反平面切口终止边和起始边弹性模量比值E2/E1=1、10、50和100时,取离散单元数n=20,采用DQM计算角度非均匀材料反平面切口尖端区域第1阶应力奇异特征指数值如表3所示。表3计算结果表明:当角度非均匀材料的弹性模量按照倒数形式变化时,采用本文DQM 获得的反平面切口应力奇异性指数计算值与文献[3]计算结果亦完全一致,因此,DQM 求解角度非均匀单相材料反平面V 形切口应力奇性指数是一种有效且准确的手段。

表3 弹性模量按照角度坐标的倒数形式变化时反平面切口的奇性指数

采用DQM 求解角度非均匀材料反平面切口应力奇性问题的控制方程,反平面裂纹和V 形切口端部前若干阶应力奇异性指数和相应的位移特征角函数一并解出。弹性模量按照指数函数和倒数形式变化分别如图3、4所示。从图3、4计算结果可知:终止边和起始边的弹性模量比值E2/E1对角度非均匀材料反平面裂纹或切口的位移特征函数影响比较明显。E2/E1=1时,均匀材料反平面裂纹位移特征角函数关于裂纹是反对称的;E2/E1=10、50时,材料非均匀性导致裂纹位移特征角函数的反对称性发生畸变。

图3 弹性模量按照指数函数形式变化时,角度非均匀材料反平面切口位移特征函数

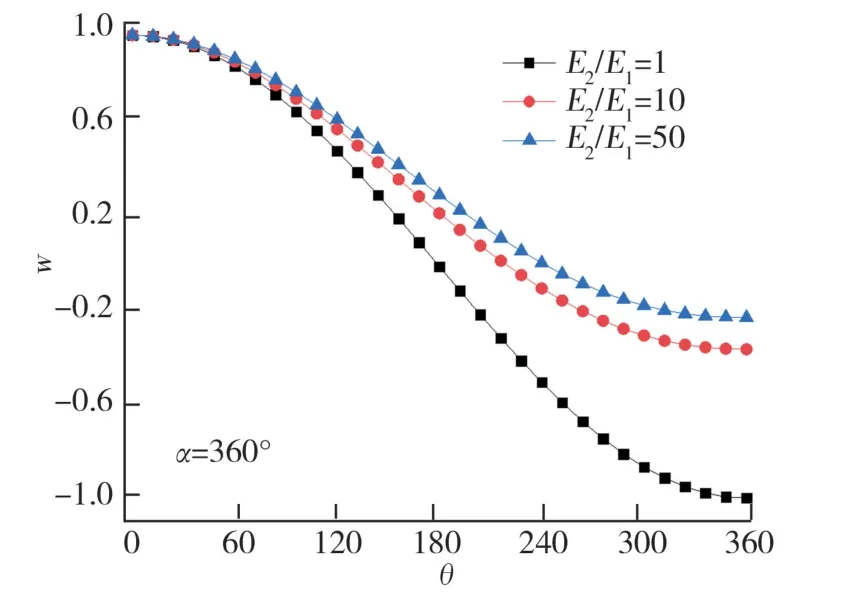
图4 弹性模量按照倒数形式变化时,角度非均匀材料反平面切口位移特征函数

3 结论

基于V 形切口端部位移场和应力场的Williams渐近展开式,将其典型项代入弹性力学反平面问题平衡方程中,将角度非均匀材料反平面V 形切口端部应力奇性指数的计算转化为一类常微分方程组特征值问题,再由DQM 求解之,可获得V 形切口和裂纹的第1阶应力奇性指数。本文主要结论如下:

(1)论文给出典型算例的DQM 计算值与已有文献结果完全一致,证明了DQM 求解角度非均匀单相材料反平面V 形切口应力奇性指数是一种有效且准确的手段。

(2)采用DQM 既可求解角度非均匀材料反平面切口应力奇性指数,同时,相应的位移特征角函数一并解出。角度非均匀材料切口的终止边和起始边的弹性模量比值E2/E1对角度非均匀材料反平面裂纹或切口的位移特征函数影响不容忽略,且材料非均匀性会导致裂纹位移特征角函数的反对称性发生畸变。

(3)基于本文的计算结果,在V 形切口外围使用有限元或边界元等数值方法离散,可以计算出切口或裂纹端部完整的奇异应力场,为评价含切口结构的安全性提供依据。