基于线性扩张观测器的双有源桥变换器自抗扰控制
高深奇
(上海电力大学 自动化工程学院,上海,200090)
0 引言
近年来,随着直流配电、储能、分布式能源等技术的应用与发展,其中的关键装置—双向隔离型直流变换器也受到广泛的关注[1],双有源桥(DAB)变换器因其具有双向功率流,高功率密度,易于实现零电压开关,便于进行级联和并行处理等优点,逐渐成为双向直流变换器的研究热点[2]。
实现DAB 变换器在输入电压波动、输出侧负载扰动等复杂工况下的动态响应和抗扰性能具有非常重要的意义[3]。目前传统的闭环控制策略为PI 控制,该控制器虽然可以稳定输出电压,但PI 控制的误差反馈会使控制量延迟.目前,除使用PI 控制器外,提高系统稳定性的控制方法还有滑模控制[4]、模糊神经网络预测[5]等,虽然这些方法优于传统的PI 控制,但由于它们过于依赖控制系统模型的参数以及固有频率等,因此其应用仍受到一定的限制。
自抗扰控制(Active Disturbance Rejection Control,ADRC)是一种基于现代控制理论的控制策略,不依赖对象的精确内部信息,具有结构简单、适应性强等优点[6],它能够很好地解决PI 控制器存在的响应快速性与超调量之间的矛盾,具有动态响应好、抗干扰能力强等特点。2018年,高志强等提出了一种线性自抗扰控制方法(LADRC),该方法可大大简化ADRC 参数的整定[7],并可为其他学者研究自抗扰控制提供良好参考。基于上述研究,本文针对DAB 变换器设计了一种基于线性自抗扰控制(LADRC)控制策略并通过仿真验证了其具有良好的控制效果。
1 双有源桥变换器系统建模
■1.1 拓扑结构
图1 为DAB 变换器的电路拓扑结构,DAB 变换器由通过高频变压器T 连接的初级桥H1(S1-S4)和次级桥H2(S5-S8)组成。L 为传输电感;U1和U2分别是初级侧输入电压和次级侧输出电压的直流电压;R2为DAB 变换器等效负载,为纯电阻性负载;C1是输入侧的保护电容,C2是输出侧的支撑电容;i1、i2和i0分别为变换器的输入电流、输出电流和负载电流,iL为流过等效电感L 的电流;变压器的变比为K=n:1。
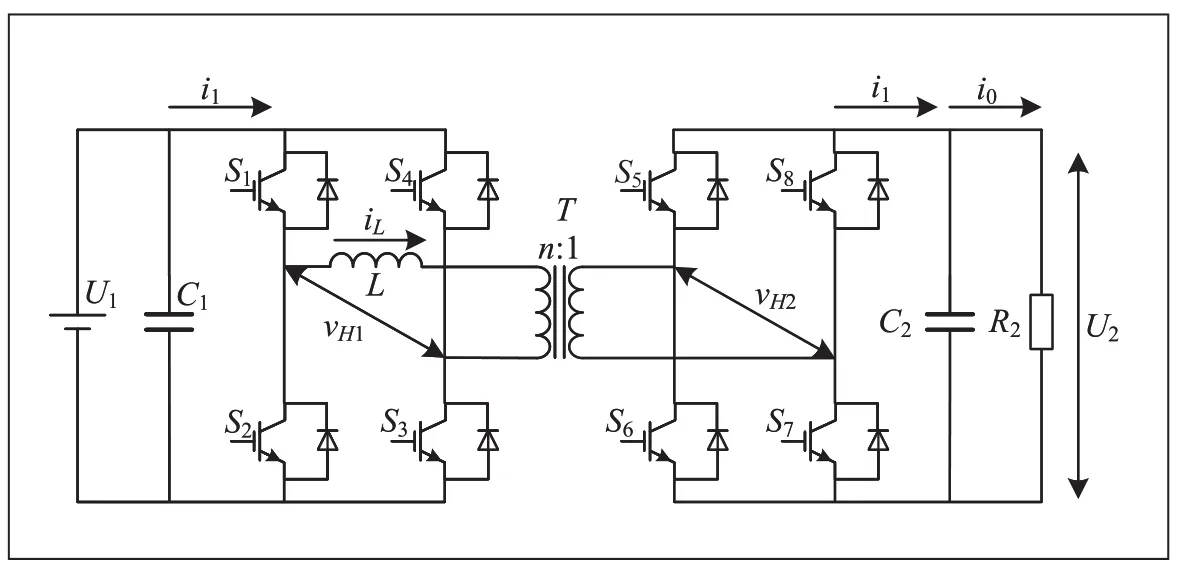
图1 双有源桥DAB 变换器拓扑图
■1.2 移相控制
使用单移相(Single Phase Shift,SPS)控制时,DAB变换器的稳态波形如图2 所示。图中S1-S4 和S5-S8 为对应的开关控制信号,每个全桥中对角开关管以50%的占空比交替导通,两全桥之间存在移相时间DTh,其中Th为半个开关周期,D ∈(-1,1)为移相比。能量经过电感L 暂存并由变压器进行电压变换,从超前侧流向滞后侧。
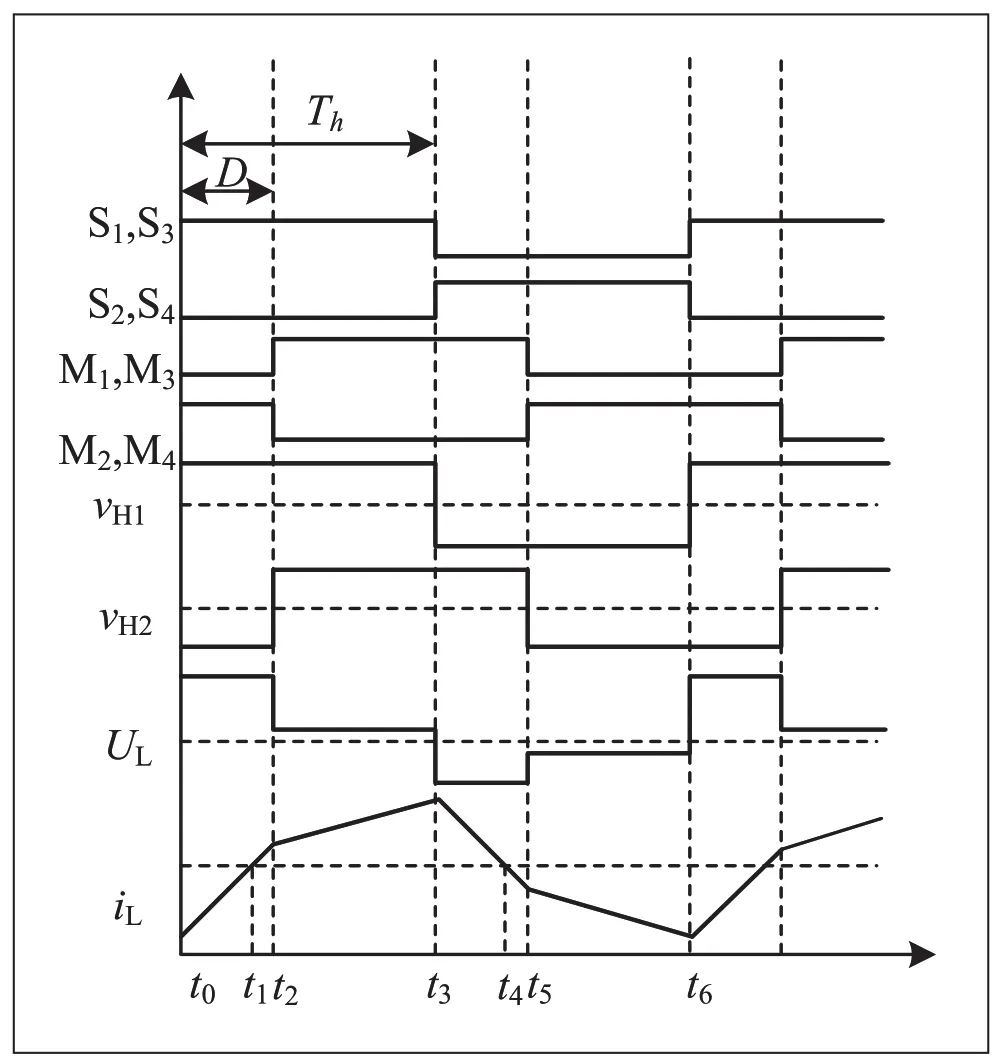
图2 单移相控制稳态时的波形图
在一个周期内,根据DAB 功率定义式,可以得到在SPS 控制下DAB 变换器传输功率表达式为:
由于DAB 变换器在高频变压器两侧的转换电路是对称的,上面的分析方法亦可得到在DAB 反向传输时的功率表达式,所以可得到DAB 变换器在传输功率时总的功率表达式:
D>0,表示功率正向传输;D<0,表示功率反向传输。
根据功率表达式(2)可以绘制出移相比D 与输出功率P的关系图,如图3 所示。
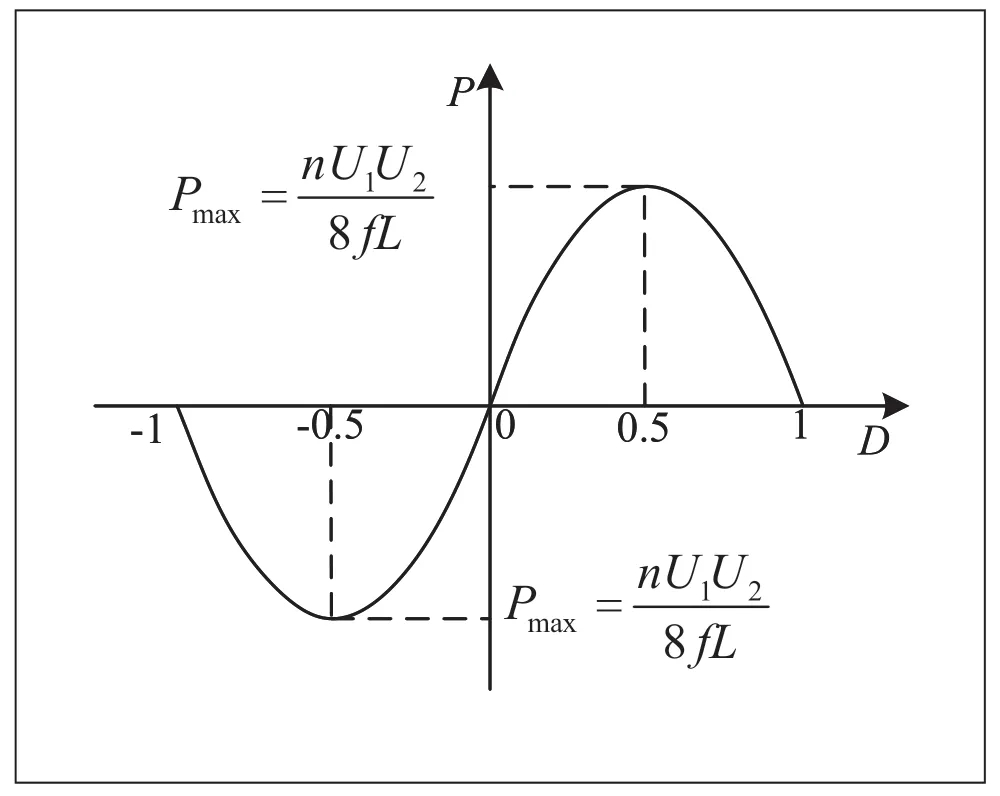
图3 单移相控制稳态时的波形图
从图3 中可以看出,传输功率P 与移相比D 呈抛物线关系。当传输功率在反向传输能量时,D ∈(-1,0),传输功率的绝对值随着移相比的增大先增大后减小;当D ∈(0,1),功率正向传输,传输功率的绝对值的变化与反向传输时一样。从图3 可以看出,传输功率有最大值nU1U2/8fL,当且仅当D=±0.5 时。
在能量传输的过程中若不考虑各种器件的能量损耗,那么可认为系统的输入功率等于其输出功率,此时输出侧的功率可以用式P2=/R2表示,其中R2表示输出侧的负载电阻。由式(2)和输出侧的功率表达式可得出输出侧系统的电压表达式为:
如果用输出电流的平均值乘以负载的等效电阻来表示输出功率,则可以得到输出电流平均值的表达式为:
■1.3 小信号模型
由于DAB 变换器的电感电流为纯交流,平均值为0,经典平均模型无法准确描述电感电流动态。因此忽略电感电流动态建立降阶平均模型。
通过在DAB变换器稳态模型的基础上引入小信号扰动,然后再分离出扰动并忽略二次项的方法,得到DAB 变换器的一阶小信号模型。
为引入低频小信号扰动,将式(4) 得到的输入、输出电流以及移相比表达式加入扰动量U1→U1+,U2→U2+,I1→I1+,I2→I2+,D →D+d^,消除公式中存在的直流量和高阶扰动,可以得到如下表达式:
其 中:b1=nU2(1-2D)/2fL,b2=nD(1-D)/2fL,b3=nU1(1-2D)/2fL。
由此可以得到DAB 小信号模型如图4 所示。
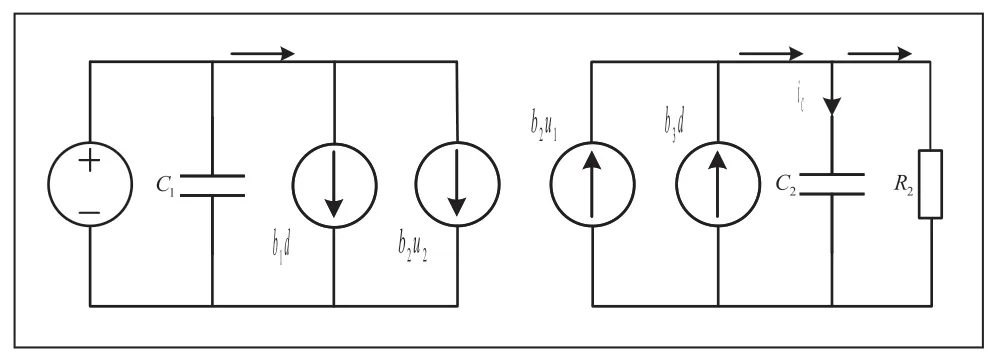
图4 DAB 变换器小信号模型
根据图4,可以得到DAB 控制量到输出的传递函数:
通过在PLECS 中搭建开环仿真模型,利用Multitune扫描系统的频率响应,再根据频率响应数据拟合出DAB 变换器的传递函数。在控制信号中施加额定控制量的1%的小信号扰动,观察输出电压在扰动频率处的幅值和相位增益。在MATLAB 脚本文件中设置拟合出的传递函数阶数为一阶的形式:
图5 给出了将扫频法与降阶小信号法获得的模型在伯德图中进行比较的结果。
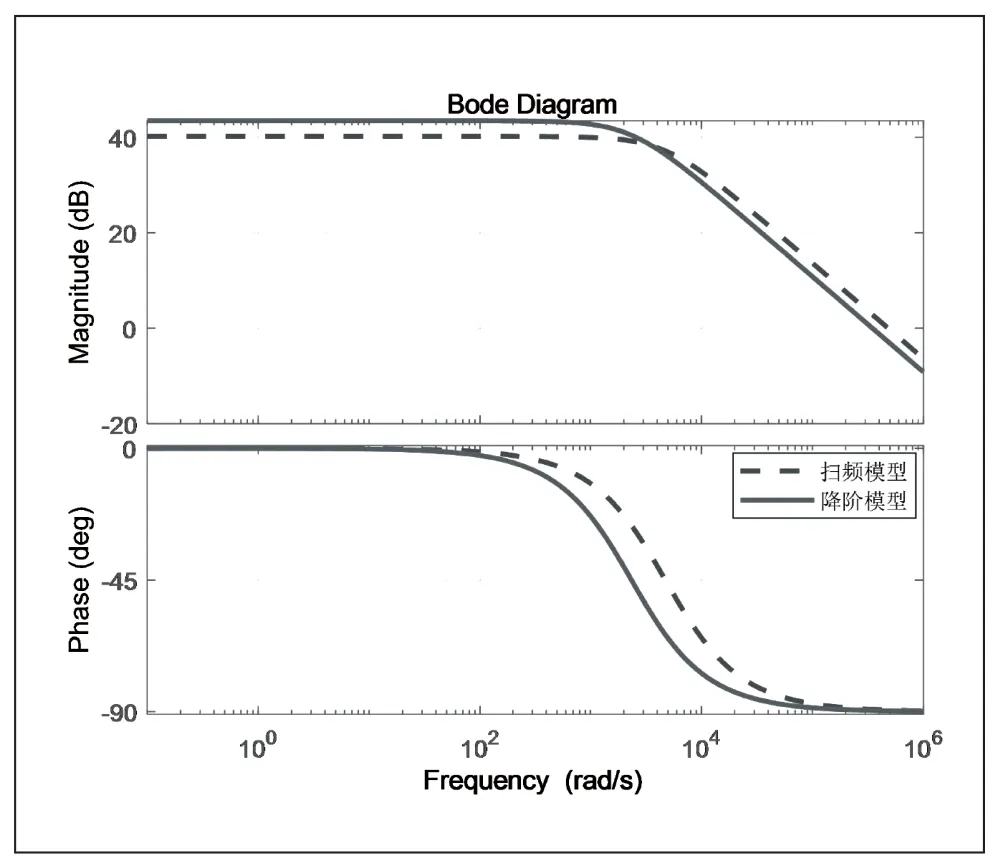
图5 扫频模型与降阶模型对比Bode 图
从图5 可以看出,根据降阶小信号模型法可得到DAB变换器建模较为精确的结果。
2 控制器设计
根据降阶模型法可得到DAB 变换器的一阶系统,因此设计一阶自抗扰控制器。根据式可以写出DAB 变换器的时域表达式为:
将表达式写成如下形式:
由于控制器控制目标为维持输出电压稳定,控制量为移相比D,所以y 表示变换器的输出电压,控制器的输出u表示移相比D;w 为系统内外部的扰动,a1 为DAB 变换器内部参数(a1 和w 均未知);b 为输入控制增益,则上式可以写成:
选取状态变量x1=y,x2=f,令h=(y,w),可得系统状态方程:
建立LESO 状态方程表达式为:
式中z1,z2为LESO 的状态变量;β1,β2为观测器增益参数。其中z1→x1,z2→x2,h 是未知的,但可通过LESO 进行估计,所以一般在LESO 的状态方程描述中可以忽略。如果参数选取的比较合理,可以使得LESO 中的状态变量很好地实时跟踪到系统状态变量。
一阶系统并不需要观测系统状态变量的微分信号,故一阶线性误差状态反馈律(LESF)为:
kp是比例系数,u0经扰动补偿形成控制量u,表达式如下:
通过极点参数配置的方法,将观测器的增益矩阵与观测器的带宽相联系。将式(12)的极点配置在LESO 的带宽 0ω上,即:
通过合理的配置扩张状态观测器的增益β1和β2,LESO能够对目标的状态和扩张状态进行实时地估计。
根据式(9)(12)(13)可以得到系统的LADRC 的内部详细的控制结构图,如图6 所示。
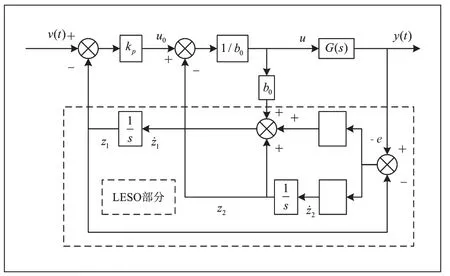
图6 LADRC 内部详细结构图
参数整定和时域仿真均在PLECS 软件中进行。基于线性扩张观测器的自抗扰控制器有kp、ω0两个可调参数。kp和ω0分别是观测器和控制器特征方程的极点,极点的配置直接影响状态变量的收敛速度,一般要求观测器收敛的速度大于控制器收敛速度数倍。因此设定 ω0=nkp。
综上所述,通过线性状态观测器(LESO)估计得到的扰动,采用状态误差反馈控制律(LESF),对误差反馈量进行实时扰动补偿,从而提升系统的抗干扰能力。
3 电压控制效果验证
基于上文对变换器拓扑的研究以及闭环控制器的设计,设计实验观察系统分别在PI 和LADRC 控制器下的输出波形,搭建了仿真验证,以验证该控制方法在启动过程、负载波动时的有效性。DAB 变换器电路参数如表1 所示。

表1 DAB变换器电路参数
根据表1 设计电路参数并利用PLECS 搭建闭环控制系统,在0.035s 和0.07s 分别进行负载投切。将PI 与LADRC 两种控制效果进行对比,整体输出电压变化、启动过程、负载投切如图7、图8、图9、图10 所示。
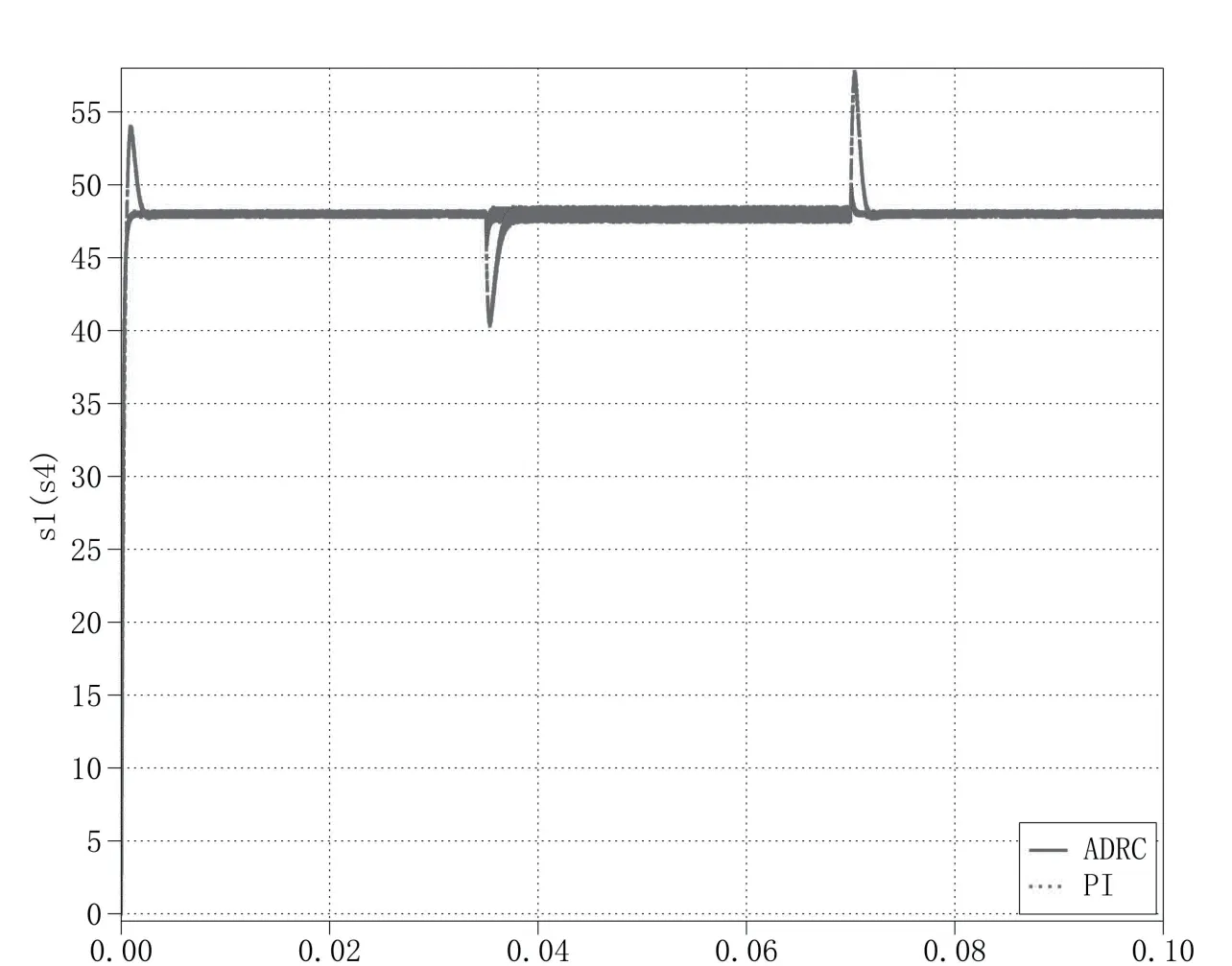
图7 输出电压波形图
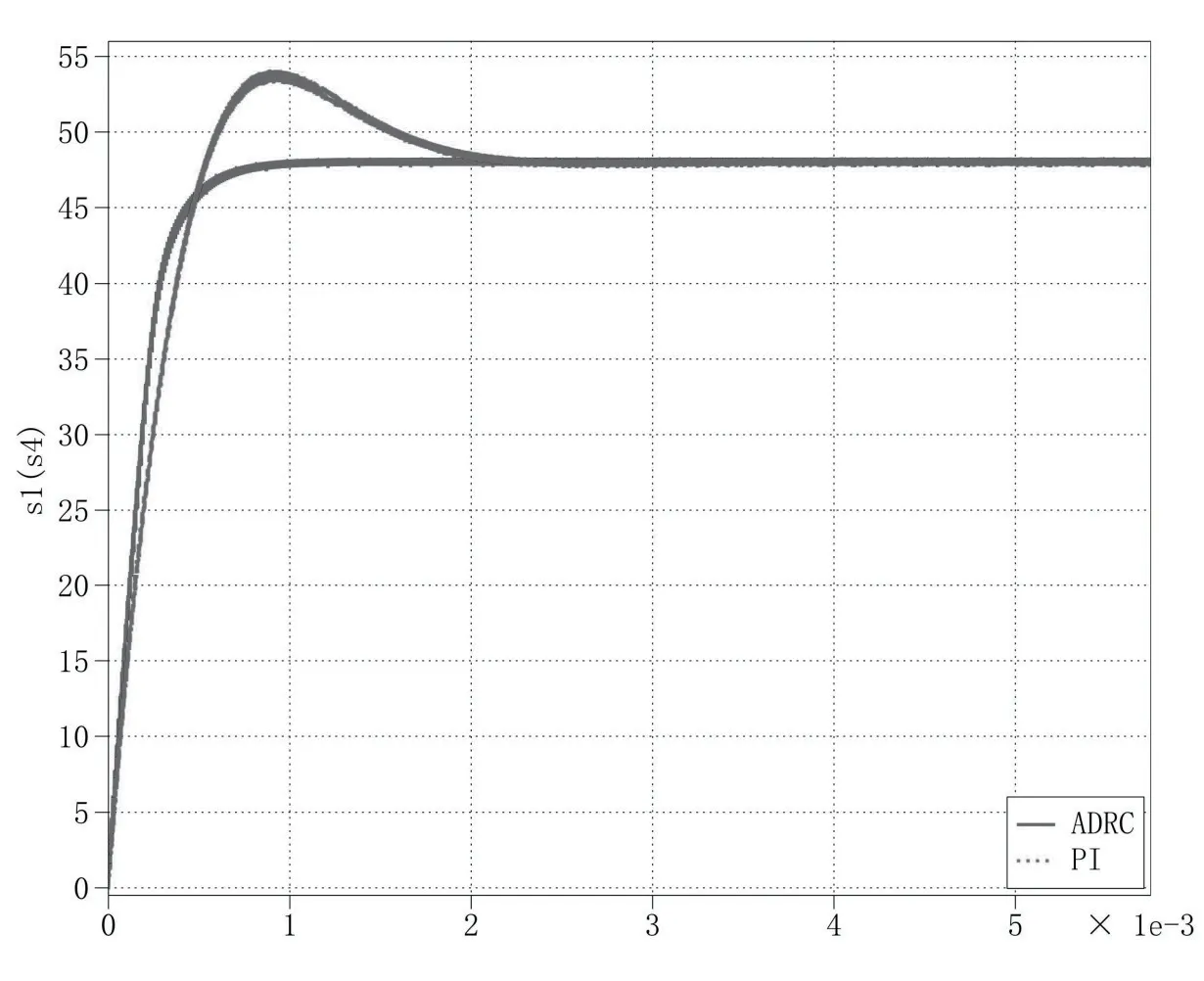
图8 启动过程
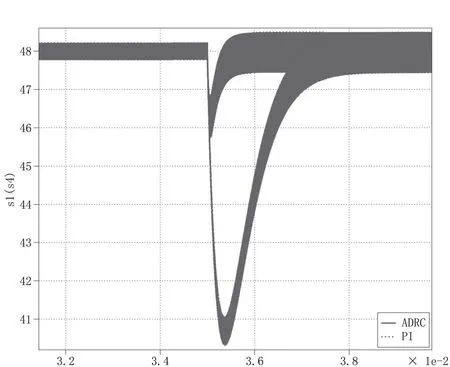
图9 负载投入
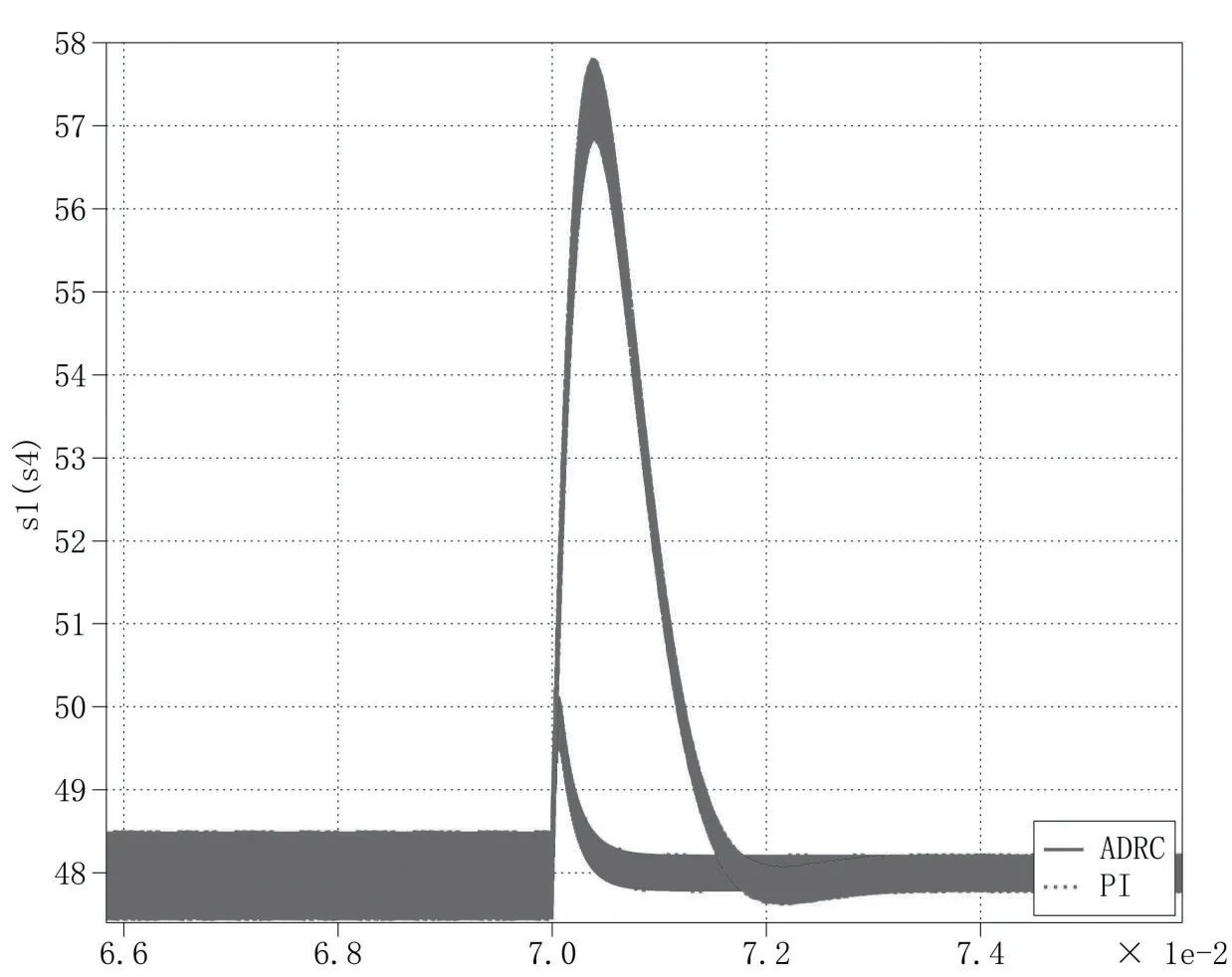
图10 负载切除
两种控制方法均可以在负荷波动时控制直流母线电压稳定在5%范围内。以下进行PI 控制和基于LESO 的自抗扰控制的定量分析。
初始阶段,系统带600W 阻性负载上电时,PI 控制产生了12.5%的过冲和2.3ms 的调节时间。相比之下基于LESO 的自抗扰控制产生了0.3%的过冲,调节时间为0.9ms。
0.035s 时刻,600W 阻性负载投入时,PI 控制产生了14.5%的欠冲和3.3ms 的调节时间。相比之下基于LESO的自抗扰控制产生了1.1%的欠冲,调节时间为1.6ms。
0.07s 时刻,600W 阻性负载切除时,PI 控制产生了18.7%的过冲和3.2ms 的调节时间。相比之下基于LESO的自抗扰控制产生了0.4%的过冲,调节时间为1.2ms。
4 结语
为改善DAB 变换器的动态响应和抗扰能力,首先对其工作原理进行了研究,后对其进行了小信号建模。在此基础上,设计了一种基于LESO 的自抗扰控制器,该控制策略在启动过程和面对负载投切干扰的情况下,其抗干扰能力和快速响应能力显著优于PI 控制。因此,本文提出的控制策略在DC/DC 变换器的控制中具有良好的应用前景。

