时变条件下道路网的车辆路径优化

张晓楠，王陆宇，谭昕妮，姜帅

（陕西科技大学 机电工程学院，西安 710021）

时变条件下基于道路网的车辆路径优化问题（Time dependent vehicle routing problem under road network, TDVRPRN）是在时间依赖型车辆路径问题（Time-dependentvehicle routing problem，TDVRP）的基础上，又综合考虑了道路网络而展开的研究。TDVRPRN 是TDVRP 和基于道路网络的车辆路径问 题（Vehicle routing problem under road network,VRPRN）的扩展，也属于NP 难题[1-2]。现实中, 受城市早晚交通高峰、路段限速和意外事故等影响，不同时段内任意两节点间的旅行时间不同，出现跨时段特征[3-4]。同时，配送车辆在道路网络上行驶，路线安排受道路网络通达性的影响，如道路单双向限行策略、节点间连通性等。因此，研究TDVRPRN 具有重要的理论与现实意义[5]。

目前还没有关于TDVRPRN 的研究，但与TDVRPRN 相关的TDVRP 和VRPRN 已有相关研究。在TDVRP 方面，Malandraki 等[6]采用阶段函数表示时间依赖性，在该策略下，旅行时间在跨时段时产生跳跃, 而实际旅行时间应随时间连续变化。Hill 等[7]提出了基于旅行速度阶段函数的处理方法以避免旅行时间在跨时段时产生跳跃。然而，这两种处理方法均不满足先入先出（ First-in-first-out,FIFO） 准则，为此，李妍峰[8]提出满足FIFO 准则的一类处理通用跨时段的方法, 研究了时变网络环境下旅行商问题，并构造了跨时段情形下的动态搜索优化算法。唐金环等[9]考虑碳排放，研究考虑旅行时间和碳排放量的多目标车辆路径问题；赵志学和李夏苗[10]考虑电动车配送的技术条件限制，研究了时变交通下的电动车城市生鲜配送路径问题；刘长石等[11]将TDVRP 与联合配送相结合，综合考虑油耗、碳排放与联合配送模式等因素，研究时变路网条件下联合配送的开放式时变车辆路径问题；侯登凯等[12]将TDVRP 与多中心车辆路径问题和混合车队车辆路径问题结合。在VRPRN 方面，李妍峰等[13-14]在研究旅行时间实时更新的动态车辆路径问题时涉及了道路网络，实验在Sioux Falls 道路网络下展开，并提出了关键节点更新策略。葛显龙和张慧[15]在研究实时交通路网车辆路径优化问题时基于重庆市道路网络展开。

通过梳理以上相关文献可见：1）近几年已出现TDVRP 与其他问题（如联合配送[11]、多中心配送[12]、混合车辆配送[12]）的结合，但还没有关于TDVRPRN的研究，而该问题是现实存在的，需通过更深入研究才能解决。2）现有关于道路网络的相关研究均是在实时动态旅行时间VRP 中涉及，而其他VRP 扩展问题在道路网络上的研究还没有（TDVRP 与实时动态旅行时间VRP 区别在于，在TDVRP 中，路段行驶时间随时间变化但事先可以通过预测确定[13-14]）。基于以上，在时变车辆路径问题基础上，考虑车辆行驶的道路网络，研究时变条件下基于道路网的车辆路径优化问题。首先，考虑车辆行驶速度的时变特征，通过构建旅行速度的分段函数，采用跨时域的方法利用离散速度计算动态旅行时间；其次，基于关键节点的概念构建道路网络，克服VRP 考虑道路网络时存在的维度灾问题；然后，结合时变旅行时间和基于关键点构建的道路网路建立TDVRPRN 的数学模型，设计蚁群算法求解；最后以西安市未央区桶装水配送区域实例进行测试，验证了模型和算法的有效性。

1 问题描述及模型建立

1.1 问题描述

TDVRPRN 问题如图1 所示，其中，方形表示配送中心，蓝色圆圈表示客户服务点，白色圆圈表示网络节点且未产生服务需求。从图1 中可以看出：

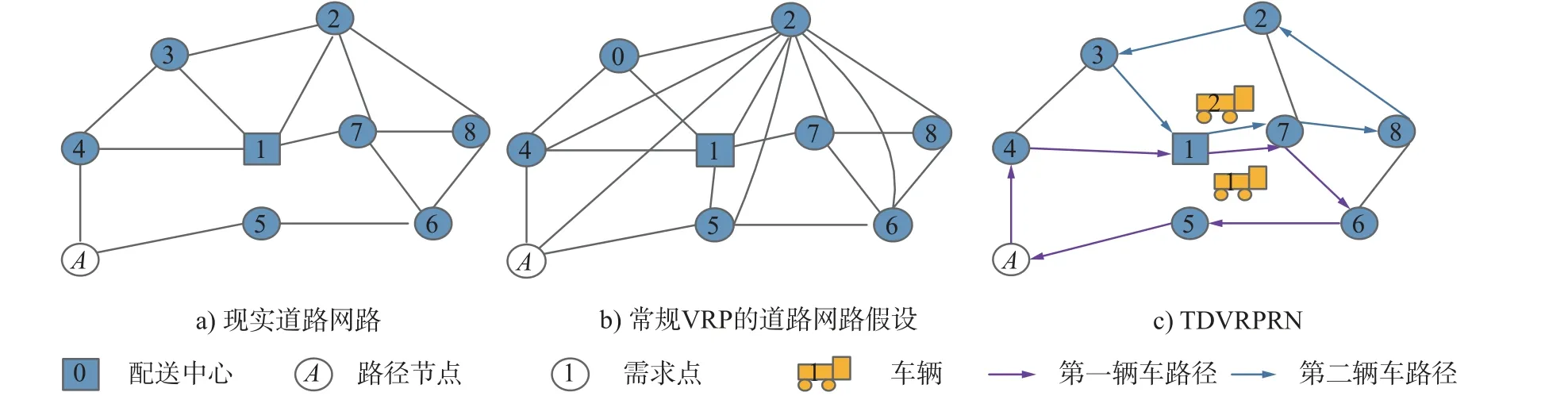
图1 TDVRPRN 示意图Fig.1 Diagram of the TDVRPRN

1）客户2 仅与客户3、配送中心1、客户7 和客户8 有直接的路径相连，与其他节点则没有；

2）网络中没有配送中心到需求点5 的直接服务路线，若车辆要去客户5 服务，仅能从节点“A”或者节点“6”绕过去；

3）其他节点同理。

为了更好地理解该道路网络，图1b）以客户2 为例展示了常规VRP 研究中道路网络假设，也就是说，在常规VRP 中，假设所有节点之间均是连通的，这与实际不符。图1c）是基于图1a）的道路网络的旅行时间时变车辆路线示意图。

从图1 还可以看出，1 个配送中心和7 个客户 的配送网络结构涉及8 个网络节点（网络节点数≥客户需求点数）。在现实中，若考虑道路网络，有限个服务需求点的配送网络可能涉及庞大的道路网络节点。由此可见，在考虑道路网络下，网络节点繁多，路径优化复杂程度成指数级增加。基于此，本文将其简化为单车辆的TDVRPRN，即TDTSPRN（Time dependent travelsale problem under road network,TDTSPRN）。将VRP 简化为TSP 是现实且可行的，如，学术界文献[8]就是针对时变网络环境下旅行商问题展开的研究；现实中，很多物流公司按照街道等行政区域将服务区域划分至各个配送员，然后再对每个配送员的服务路径展开具体优化。

TDTSPRN 可以描述为：配送系统有1 个配送中心和n个客户，配送中心编号为1，客户集合C={2, ···,n+ 1}。车辆从配送中心出发对n个客户组织配送。网络中的道路节点集合为N，N={1,C,N0}，其中N0为车辆可以在该点改变行驶路线的网络节点，一般默认该点不会产生服务需求。求解的目的是在满足客户需求的基础上，合理安排配送车辆的行驶路径，使得总旅行时间最短。其他相关假设为：车辆从配送中心出发完成配送服务后返回配送中心；每个客户只能被服务一次；交通路网具有时变特性，配送车辆在不同时间段内以不同时速行驶，且当车辆遇到交通拥堵，按照先进先出原则随车流缓慢行驶。

1.2 符号定义

TDTSPRN 模型中的所有符号如表1 所示。

表1 符号定义Tab.1 Definition of notations

1.3 时变旅行速率的动态旅行时间确定

这里考虑车辆旅行速度的时变特征，把一天分为几个时段，给出车辆在不同时段内的分段函数，采用跨时域的方法利用离散速度计算车辆在任意两节点间的旅行时间。通常情况下，时间段的划分需要很短，如15 min，这样才能将该时段内的车辆平均速度视为该时间段内的固定速度。这种方法可确保车辆根据FIFO 规则沿弧线行驶。图2 是相应的旅行速度分段函数，图3 是不同时间段的车辆行驶距离和行驶时间。

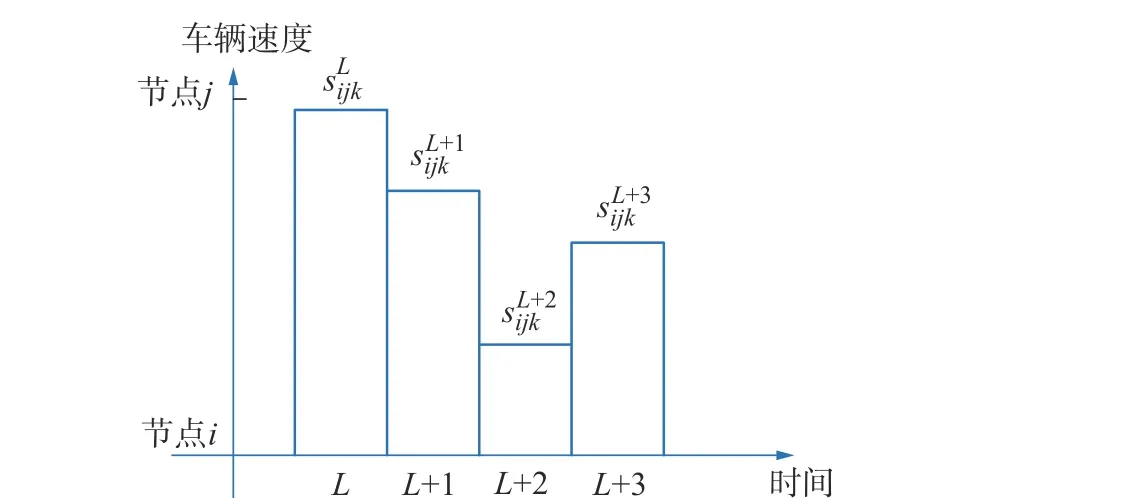
图2 不同时间段车辆行驶速度Fig.2 Vehicle traveling speed at different time periods

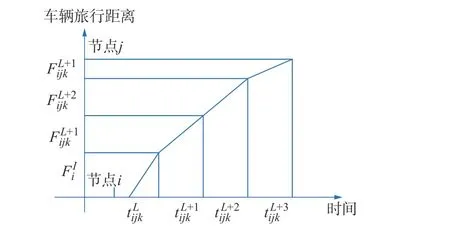
图3 不同时间段车辆行驶距离和时间Fig.3 Traveling distance and time at different time periods

假设di∈ [TL-1，TL],则tij的详细计算步骤如下：

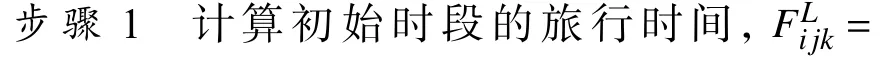
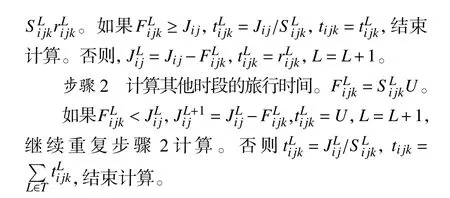
1.4 关键点的道路网络确定

为了克服车辆路径问题在考虑道路网时存在的维度灾问题，提出一种基于关键节点的概念来构建道路网络，即在实际道路网络的基础上，选择车流量较大的路径交叉节点作为路网中的关键节点。假定车辆从节点A出发到达节点B，图4 中的节点表示为实际路网中的交叉路口，实线线段表示为实际路网中的可通行路段，虚线线段表示实际路网中的不可通行路段，由此可看出，从节点A到节点B之间存在包括A、B在内的49 个路径交叉节点，因此车辆从A到B的路径选择有O(449)种方案。图5 是基于关键节点的道路网络，其中，实心原点表示选择的路径关键节点，可以明显看出，基于关键点道路网络的路径选择急剧减少，可见，该策略可行。

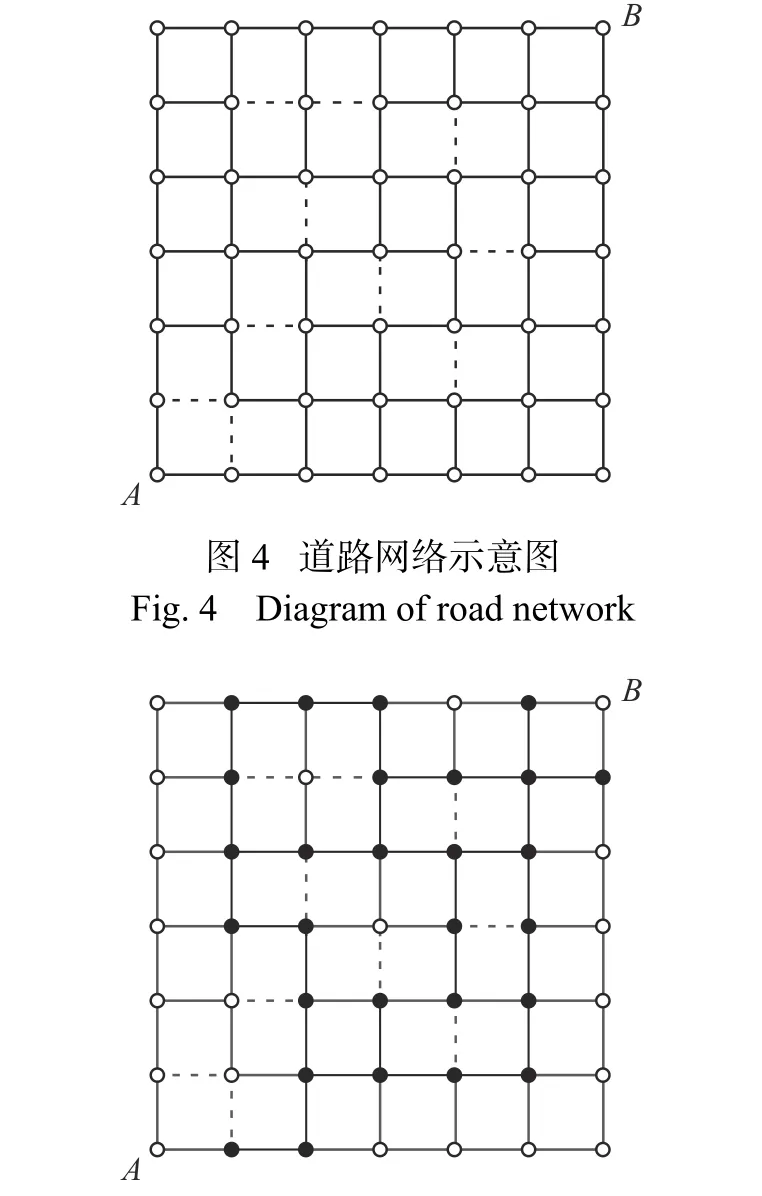
图5 基于关键节点的道路网络示意图Fig.5 Diagram of road network based on key nodes

1.5 模型建立

基于以上，建立如下模型：

式（1）为目标函数，目标函数表示总旅行时间最短；式（2）和式（3）表示车辆到达和离开的是同一个节点；式（4）表示车辆到达节点的时间等于离开节点的时间；式（5）表示车辆在第L时间段行驶的距离不大于弧线e(i,j) 的 总距离；式（6）表示弧线e(i,j)的总距离为各个时间段车辆行驶距离总和；式（7）表示在第L时间段车辆的旅行时间等于在该时间段车辆的行驶距离与旅行速度之比；式（8）表示车辆在第L时间段的实际行驶时间不大于车辆行驶完弧线e(i,j) 的 总时间；式（9）表示车辆行驶完弧线e(i,j)的总旅行时间为各个时间段车辆行驶时间的总和；式（10）表示车辆离开j节点的时间；式（11）表示子回路约束；式（12）和式（13）表示符号和决策变量的约 束。

2 算法设计

蚁群算法是一种全局搜索算法，当搜索最优解时，能通过信息素的来进行信息的交互，继而实现同时在不同空间进行搜索。文献[16-17]已经证明了该算法有较强的全局搜索能力，适用于在求解VRP及其扩展问题。鉴于此，本文采用蚁群算法求解TDTSPRN 模型。蚁群算法流程如图6 所示。

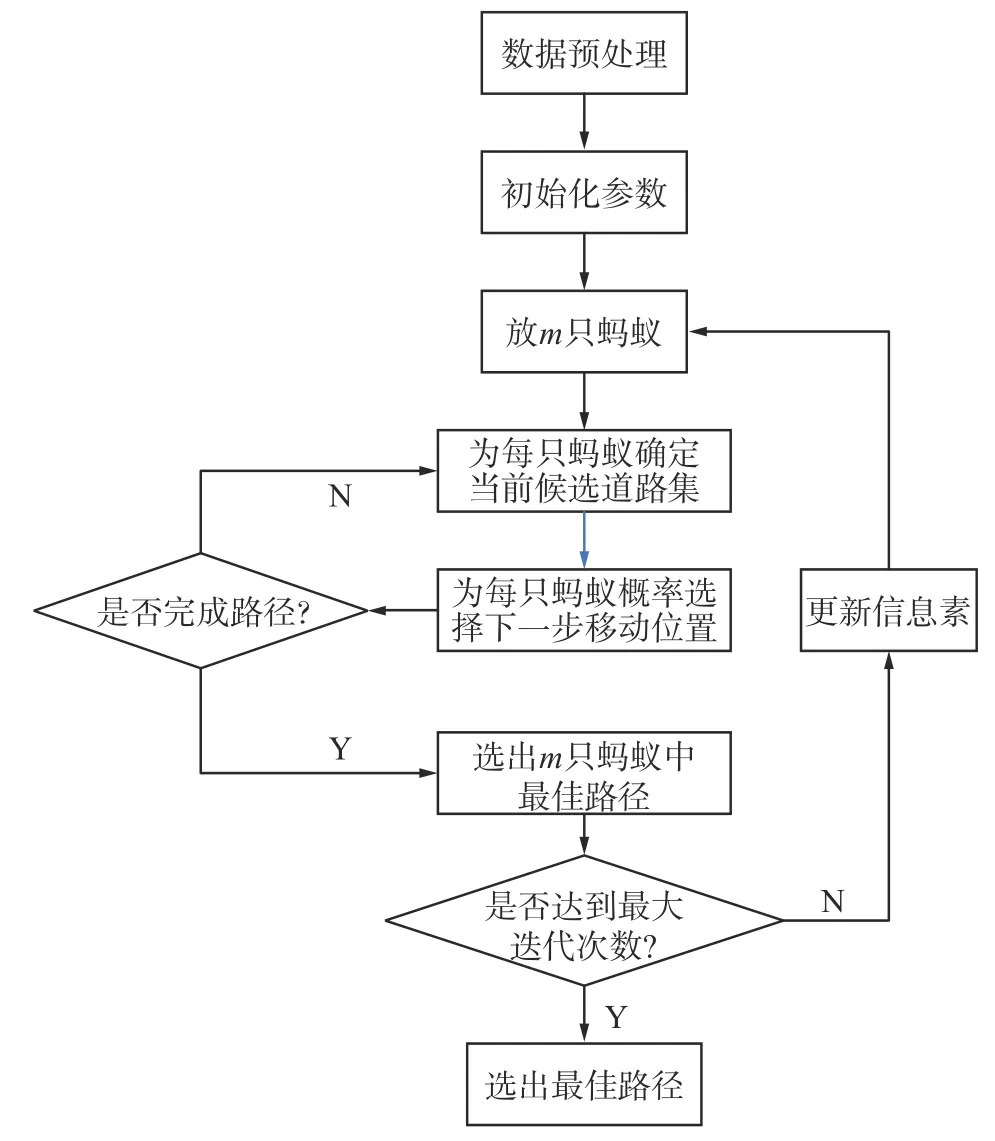
图6 蚁群算法流程图Fig.6 Flow chart of ant colony algorithm

1）初始化算法所有参数和变量。输入最大迭代maxgen ， 蚂蚁总数m， 信息素重要程度因子 α，启发函数重要程度因子 β，信息素的蒸发因子ρ。令当前迭代次数 gen=1。

2）构建可行的方案。

步骤1 将m蚂蚁放入配送中心中，定义tabum表示蚂蚁m的 禁忌列表，令 tabum=∅。

步骤2 蚂蚁m依次从配送中心出发，将当前蚂蚁所有还没有访问的节点放入集合 a llowedm。

步骤3 依据时变旅行速度分阶段函数，计算当前时刻下两点间的旅行时间tij，并计算车辆到达节点J的时间aj。

步骤4 计算车辆从当前节点行驶到节点的转移概率。蚂蚁m根据信息素和信息素组成的状态转移概率函数Pmi j，使用轮盘赌的形式从当前节点选择下一个节点进行访问。蚂蚁m移动的概率Pmij从当前节点i到下一个节点j定义为：

式中：参数 α ， β用于权衡各个因素以指导搜索过程；ηij为启发式因子，定义 ηij=1/tij。

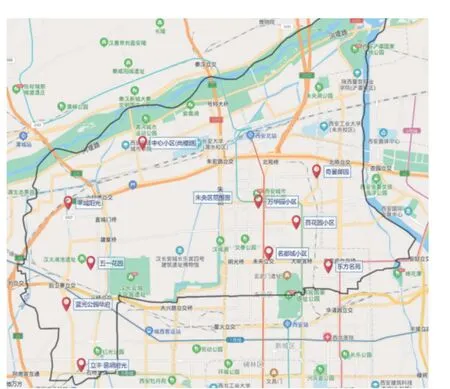
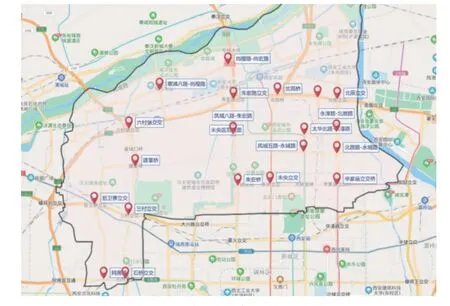
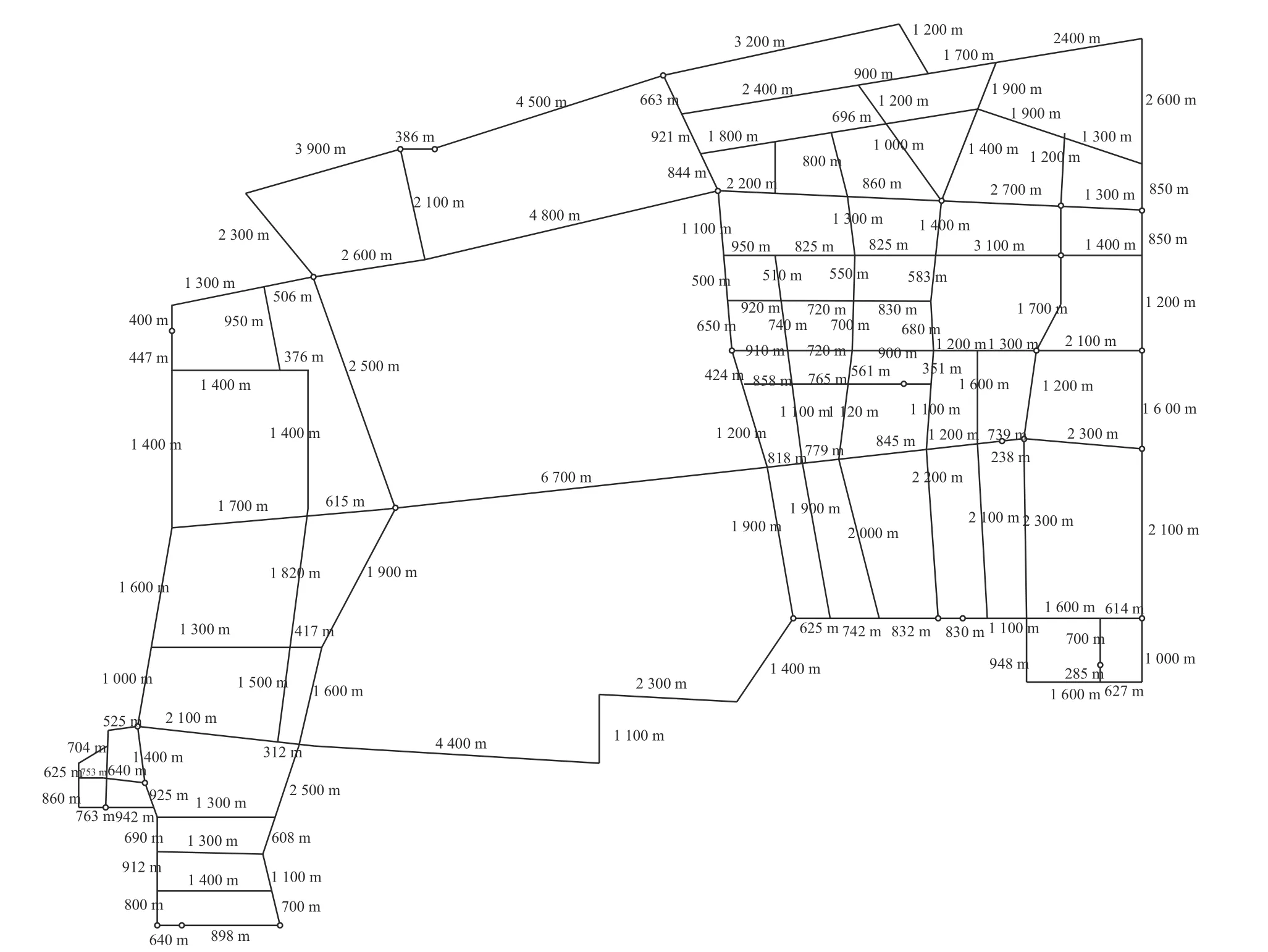
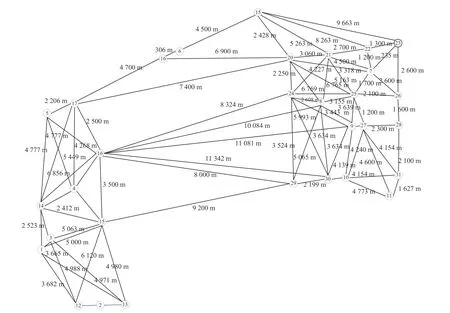
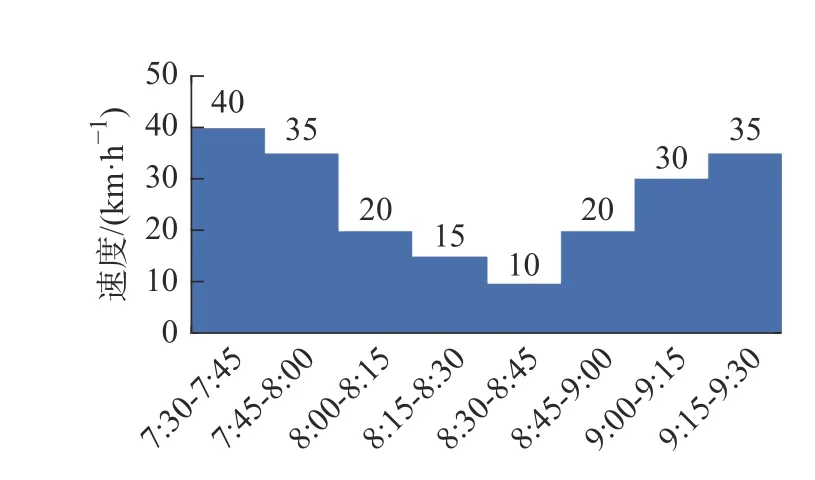
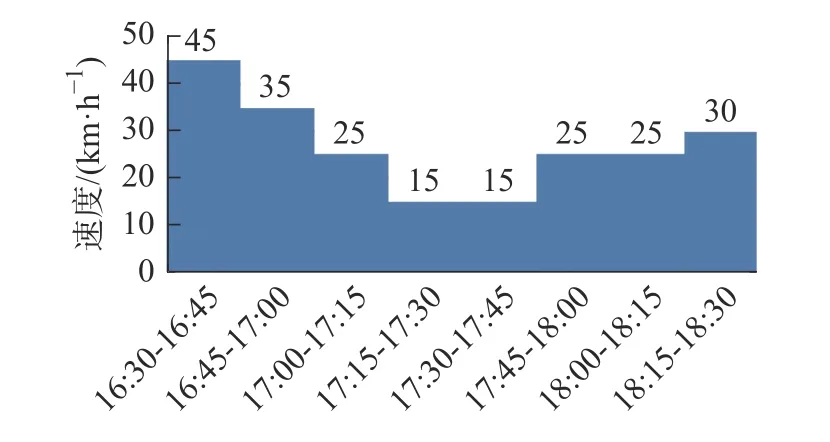
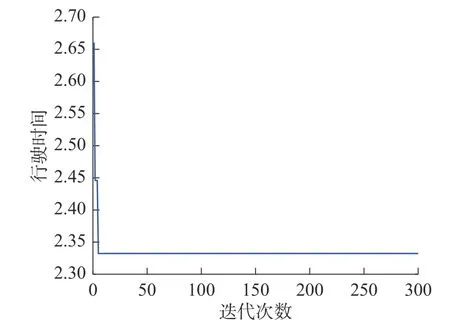
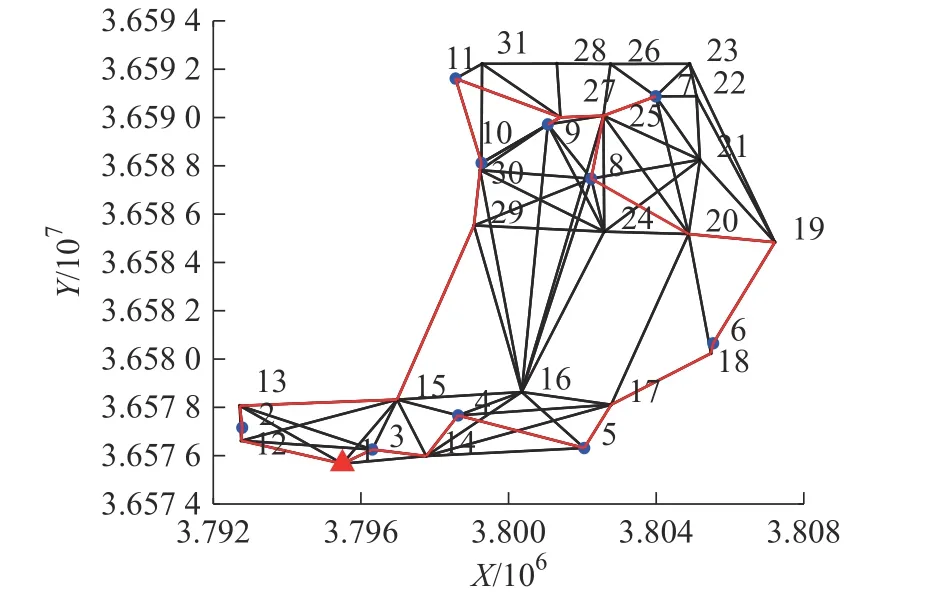
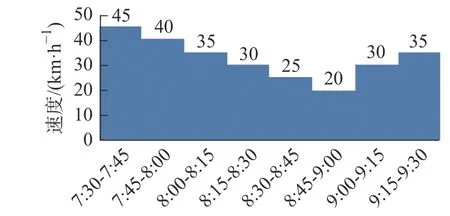
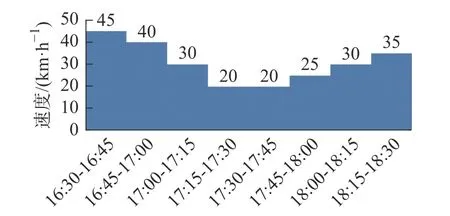
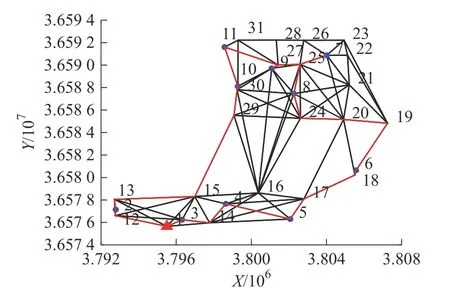
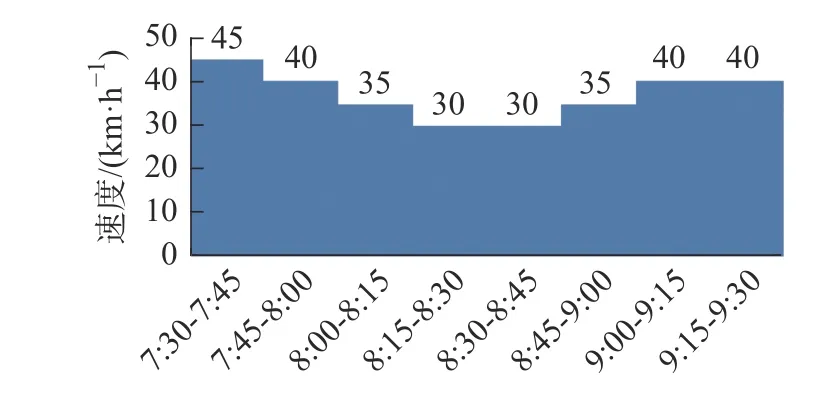
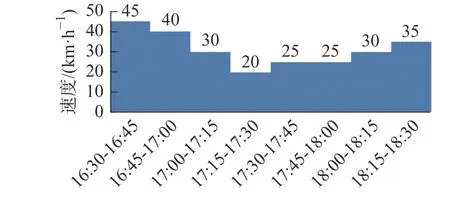
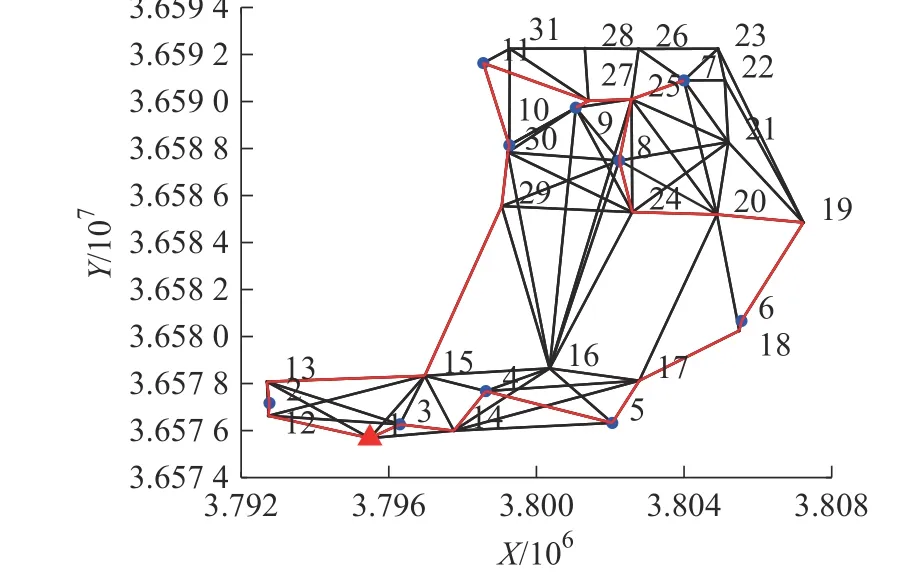
5）算法终止。如果 gen

3 实例测试

3.1 实例描述

本文以西安市未央区桶装水配送中心及其服务的10 个需求点为例，图7 为服务的10 个需求点，图8 为该配送区域内的19 个关键网络节点，这些节点来源于现有路径网络的基础上确定经常发生交通拥堵的节点。

图7 服务的10 个需求点Fig.7 The 10 demand nodes

图8 关键道路网络节点Fig.8 Key nodes at road network

3.2 道路网络

根据需求点和关键道路节点位置，图9 给出了各节点之间城市主干双向通行道路构建的关键路网示意图。图中，黑色圆圈易发生交通拥堵的19 个关键路径节点，蓝色圆圈代表1 个桶装水配送中心，红色圆圈代表10 个小区需求点。各节点之间的路径均由实际路网简化处理，车辆可在路径之间双向行驶。

图9 道路网络构建Fig.9 Load network construction

在上述实际道路网络图中，除去选定的配送中心、需求点、路径关键节点以外，还存在路径与路径之间的交叉节点，在后续的算法求解过程当中这些路径交叉节点与实际选取关键节点难以被区分。为解决此问题，本文进一步简化路网，即道路网络仅包括路径关键节点、需求点以及配送中心点的道路网络，简化后道路模型如图10 所示。

图10 基于关键点的道路网络Fig.10 Road networks based on key points

3.3 动态旅行时间

根据西安市未央区的道路交通报告，预测出西安市未央区城市主干道路在早晚高峰时间的速度随时间的变化图。早高峰速度时间图如图11 所示，晚高峰速度时间图如图12 所示。其余时间段车辆行驶速度统一为城市道路平均顺畅速度45 km/h。

图11 早高峰速度时间变化图Fig.11 Speed during morning peak time span

图12 晚高峰速度时间变化图Fig.12 Speed during evening peak time span

3.4 求解结果

采用MATLAB 2016a 编程，操作系统Windows 10，电脑内存为8G，CPU 为Intel i7-6700, 主频3.40 GHz。设置算法参数为：车辆出发时间为07：00，最大迭代次数 m axgen=300，蚂蚁总数为20，信息素重要程度因子 α=1，启发函数重要程度因子 β =1，信息素的蒸发因子 ρ =1。

图13 是本文算法的求解迭代图，算法搜索约在50 次以内趋于平稳，说明该算法能稳定收敛，算法合理有效。

图13 算法进化迭代图Fig.13 Algorithm iteration diagram

图14 是车辆旅行路径图。从求解结果来看：需求点服务顺序为“2 — 10 — 11 — 9 — 8— 7— 6 —5— 4— 3”，即车辆先服务蓝光公园华府，到五一花园、芊域阳光、中心小区（尚稷路）、万花园小区、奇星御园、百花园小区、东方名苑、名都城小区最后服务立丰昆明时光。车辆行驶路线为1— （12）— 2 —（13）—（15）—（29）—（30）— 10 —11—（27）— 9 —（27）—（25）— 7 —（25）— 8 —（20）—（19）— 6 —（18）—（17）— 5 — 4 —（14）— 3 — 1，括号中为路径关键节点，行驶路程为67.879 km。车辆07：00 从配送中心出发，09:21 回到配送中心完成配送任务。

图14 车辆行驶路径Fig.14 Vehicle routing

3.5 敏感性分析

1）旅行速度变化

由于城市交通拥堵情况越发的严重，部分城市采取了错峰出行政策，如杭州与重庆通过实施这项政策在缓解交通拥堵，较少路段通行车流量方面取得了非常不错的成绩；重庆采取错峰出行政策的第二日，中心城区的早高峰平均车速同比提升9.2%，早高峰车流量同比平均下降14.3%。另外，尾号限行制度也是各大城市缓解城市交通压力的另一重要措施。基于此，分析在政策引导下，早晚高峰旅行速度的分阶段函数改变对车辆总旅行时间影响。以错峰出行和尾号限行两种不同的交通拥堵政策可能引起的旅行速度函数用于测试。

模式1 在实施错峰出行的情况下，车辆速度下降得到一定缓解，但很长时间内车辆在节点间的行车速度不能快速恢复到日常速度45 km/h，这里以图15 和图16 为例测试。

图15 早高峰速度时间变化（错峰出行）Fig.15 Speed during morning peak time span(staggered shifts)

图16 晚高峰速度时间变化（错峰出行）Fig.16 Speed during evening peak time span(staggered shifts)

车辆旅行路径如图17 所示，可以看出，需求点服务顺序为3— 4 — 5 — 6— 8 — 7 — 9 — 11 — 10 — 2 。完整行驶路线为1— 3 —（14）— 4 — 5 —（17）—（18）—6 —（19）—（20）—（24）— 8 —（25）— 7 —（25）—（27）— 9 —（27）— 11 — 10 —（30）—（29）—（15）—（13）—2 —（12）— 1。车辆从07:00 离开桶装水配送中心，08:52 完成所有配送任务回到配送中心。可见，该模式下车辆行驶路径不变，但旅行时间缩短了29 min。

图17 车辆配送路径图Fig.17 Vehicle routing

模式2 在实施尾号限行的情况下，车辆速度下降也得到一定缓解，并能快速恢复到日常速度45 km/h，这里以图18 和图19 为例测试。

图18 早高峰速度时间变化图（尾号限行）Fig.18 Speed during morning peak time span (license plate restrictions)

图19 晚高峰速度时间变化图（尾号限行）Fig.19 Speed during evening peak time span (license plate restrictions)

车辆旅行路径图如图20 所示，可以看出：需求点服务顺序为3 — 4 — 5 — 6 — 8 — 7 — 9 — 11 — 10 —2 ；完整行驶路线为1— 3 —（14）— 4 — 5 —（17）—（18）— 6 —（19）—（20）—（24）— 8 —（25）—7 —（25）—（27）— 9 —（27）— 11 — 10 —（30）—（29）—（15）—（13）— 2 —（12）— 1。车 辆 从07:00 离开桶装水配送中心，08:47 完成所有配送任务回到配送中心。可见，该模式下车辆行驶路径不发生改变，但行驶时间缩短34 min。

图20 车辆配送路径图Fig.20 Vehicle routing

从以上两种模式求解结果对比可以看出：车辆旅行速度的改变并不会引起车辆优化路径的改变，但对总旅行时间影响较大。说明，伴随着城市为缓解拥堵的各项交通政策的实施，运输企业无需对配送路径进行重新优化，配送效率能得到极大提升。

2）出发时间变化

车辆在城市路网中的行驶速度不仅受到行驶距离与行驶路段的影响，还受到车辆出发时间的影响，如早晚高峰拥堵导致车辆在早晚高峰时间段内出发配送货物，就易遇上交通拥堵，车辆行驶速度较慢。基于此，本文进一步将通过改变原始实例中的车辆出发时间去研究怎样选择车辆的出行时间，使车辆的行驶方案能够更加优化。

表2 为不同出发时间下的目标函数值对比，从中可以看出，不同出发时间对于车辆的行驶时间影响较大，相较于07:00 出发而言，车辆从早上10:00 出发总旅行时间更短。相较于车辆出发时间为07:00 的情况下，车辆的行驶时间缩短了40 min。

表2 不同出发时间算例的目标函数值表Tab.2 Objective function values for instances of different departure time

4 结论

1）在时变VRP 的基础上，综合考虑了道路网络，建立了相应的单车辆模型，研究问题更符合实际配送的运作。

2）提出了基于关键点的道路网络构建，克服了现实道路网络的复杂性。

3）车辆行驶速度的改变并不会引起车辆优化路径的改变，但对行驶效率提升较大；相较于早上07:00 出发而言，车辆从10:00 出发总旅行时间更短，能缩减行驶时间40 min。

未来研究中将将其扩展到多车辆问题，并进一步考虑时间窗、模糊需求等因素的影响， 使问题更贴近实际配送。