考虑加工精度等级的核动力潜艇永磁电机转子结构不平衡振动响应分析

廖子豪，宾光富，李超，高耀智

（1.湖南科技大学 机械设备健康维护湖南省重点实验室，湖南湘潭 411201；2.湖南湘电动力有限公司，湖南湘潭 411101）

低速巡航是核动力潜艇常见的一种工况，其动力系统永磁电机转速一般为89 r/min，既可以提升续航里程，又可以满足巡逻侦查时潜艇的低振动隐身性能需求。低速巡航过程中因永磁电机转子结构不平衡导致的振动是核潜艇动力系统的主要振源，这种结构不平衡包括材料质量分布不均引起的材料不平衡、机械加工精度引起的结构不平衡以及装配环节引起的装配不平衡[1-3]。由于安装在转子上的永磁体产生的强磁场会干扰动平衡测试系统中传感器的测量精度，极易造成动平衡失败。因此在生产制造这类永磁电机转子过程中，通过现有平衡工艺对加工过程中产生的结构不平衡进行校正，导致出厂后转子振动值难以达标。在满足转子零部件装配精度的前提下，各零部件加工工艺的精度等级所产生的转子不平衡量不相同，从而影响转子的振动。那么，选择合适的加工工艺精度，以从源头上减少因加工精度等级所产生的不平衡量不失为一种有效的控制转子振动响应方法[4]。

国内外学者对加工精度产生的影响进行了相应的研究。Cao 等[5]建立了尺寸偏差和加工参数之间的联系。Barkallah 等[6]提出了一种基于随机变量的公差确定方法，以选择最优加工公差。孙岩辉等[7]提出通过制造误差预测轴精度的计算方法。管峰等[8]分析不同加工精度对止推轴承刚度和承载力的影响。周洋等[9]分析加工精度对齿轮啮合的接触应力的影响情况。赵丽滨等[10]研究不同制造公差下螺栓连接强度的变化情况。以上研究从加工精度对零部件受力情况进行分析研究，而从加工精度对不平衡振动响应的影响考虑较少。

因加工及装配误差等因素, 产生质心与几何中心不重合现象, 导致运转中产生的不平衡是电机转子振动的主要激振源，直接影响动力系统的可靠性和使用寿命。Zarko 等[11]对电机转子不同情况下磁拉力对振动响应变化进行建模分析。Yao 等[12]通过分析转子振动的幅值与相位，提出了一种抑制多频转子周期振动的方法。Ma 等[13]考虑陀螺效应对转子系统振动响应的影响。陈清爽等[14]对汽车传动系统进行了动平衡测试和控制方法的研究。张鑫等[15]通过开槽改变转子齿形以抑制电磁振动。周生通等[16]基于嵌入式谱随机有限元法，研究随机不平衡对转子系统振动响应特性。夏亚磊等[17]建立了某发电机转子转轴弯曲与不平衡耦合作用下的系统运动方程，分析了不平衡力与弯曲平面之间的夹角对振动的影响。以上研究多从不平衡分布情况来控制不平衡振动响应特性，从控制加工精度来减少不平衡振动响应的产生考虑较少。

根据实际工程需求，本文针对核动力潜艇永磁电机转子自身强磁性的特点以及难以在低速时进行整机动平衡的问题，在满足零部件装配精度的前提下，考虑典型加工精度等级对电机转子结构不平衡的影响，从源头上控制不平衡量的产生，构建5 种典型的加工工艺精度模型，从而得到加工精度同转子结构不平衡之间的关系，并将其关系代入实际转子结构尺寸中，得到不同加工精度下产生的结构不平衡量。然后采用有限元法，建立典型不平衡激励下的动力学模型，得到振动响应图谱，根据振动幅值大小来评价不同加工工艺精度对该大型永磁电机转子结构振动的影响。

1 加工工艺精度建模

在实际检测中，所测得的加工精度为一个区间，即加工精度以公差带的形式展现。根据核动力永磁电机转子实际加工工艺，选取5 种影响振动响应最大的典型加工工艺，建立单因素公差模型，以分析不同加工精度等级对转子振动的影响。

1.1 轴颈圆跳动公差模型

轴颈端面圆跳动公差带是在与基准轴线同轴的任一直径的测量圆柱面上，沿母线方向宽度为公差值d1的圆柱面区域。轴颈圆跳动精度主要决定加工面的垂直程度，其值影响垂轴承轴向定位和密封圈的密封性能等。由轴颈圆跳动定义以及测量方法，选取圆跳动公差d1/2 为轴颈圆跳动精度的最大和最小值，等效轴颈圆跳动公差模型如图1 所示。图1中：虚线为理想表面轮廓线，粗实线为实际表面轮廓线。

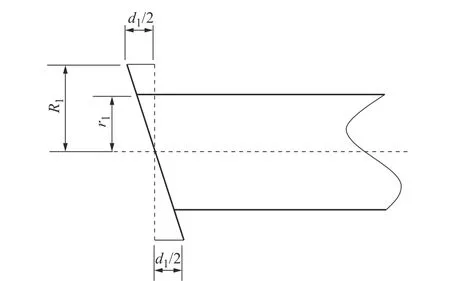
图1 轴颈圆跳动公差模型Fig.1 Circular run-out tolerance model of a journal

由模型可知，将轴颈端面偏移d1/2 后，上下两部台阶处变化的质量相反，故求得上下两部梯形回转后的体积VC为

式中：R1为轴颈阶梯处的半径；r1为转轴半径。

由式（1）可得到不平衡量UC为

式中：m1为转轴质量；e1为质心到回转中心的距离；ρ1为轴密度。不平衡量的方向为垂直回转轴线方向。

1.2 同轴度公差模型

同轴度精度考虑的是实际回转中心轴线同理想回转中心轴线之间的差值，其值影响运转时整体偏摆幅度。实际加工得到的中心轴线在公差范围内呈波浪形曲线，考虑到电机轴长度和同轴度公差比值大于18 000（即长为18 000 mm 的转轴允许回转中心轴线偏移理想回转轴线1 mm），由同轴度公差定义以及实际情况，可将实际回转轴线等效为一条直线并偏离公差值为d2/2，等效同轴度公差模型如图2所示。

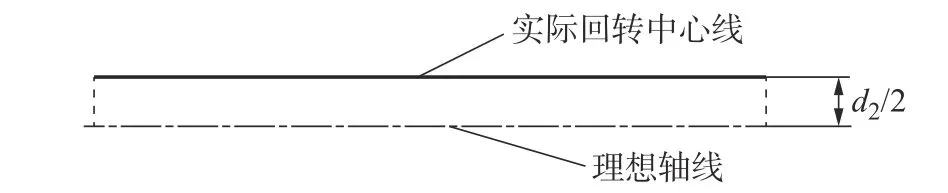
图2 同轴度公差模型Fig.2 Coaxiality tolerance model

由于同轴度公差模型未改变轴的质量，则不平衡量UA为

式中d2为同轴度公差。不平衡量的方向为垂直回转轴线方向。

1.3 平面度公差模型

平面度精度主要决定装配中两构件结合面贴合程度，其值影响连接件的预紧力，使各个连接件的预紧力不一致，易造成连接件过快疲劳失效。实际加工中，平面度为实际表面在理想面 ±d3/2 内波动。若实际表面高出理想面，可采用精磨等方式将多余质量去除，故本节主要考虑实际表面低于理想面。设实际表面不高于理想面，将转轴端面上半部分设为带公差的表面，下半部分设为理想表面，使得转轴因平面度加工精度产生最大不平衡量，其中粗实线为实际表面，虚线为理想表面，等效平面度公差模型如图3 所示。

通过对平面度精度进行等效处理，将整个端面的的差值集中至半个端面，使其形成一个球缺体，并取允许的最大平面度d3，则因平面度所减少的转轴体积VF为

式中：r3为球半径；d3为平面度公差。

设转轴直径D3，则式（4）变换为

根据所建立的平面度公差模型可知，轴段端面轴向长度减少了d3，所以只需计算轴向长度为d3，直径为D3的半球缺体质量m3与质心e3的变化即可。由式（5）可求得平面度产生不平衡量UF为

式（6）中不平衡量的方向为平行回转轴线方向。

1.4 支撑板偏斜公差模型

支撑板主要支撑转子支架外环，支撑板偏斜将影响支架外环受力，出现受力不均的现象，易使支架外环在运转时因不平衡力矩造成塑性变形影响使用寿命。本节以10 块支撑板为例，为得到支撑板偏移所引起的最大不平衡量，将相对的2 块支撑板共5组支撑板向逆时针方向水平移动偏移公差d4，支撑板尺寸变化可忽略不计，支撑板偏移等效公差模型如图4 所示。图4 中：虚线为支撑板理想位置，粗实线为支撑板实际位置。

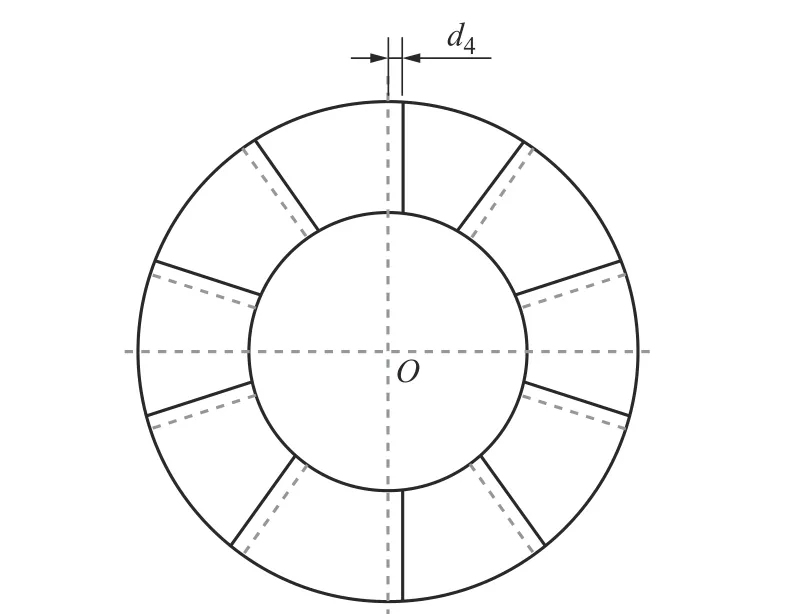
图4 支撑板偏移公差模型Fig.4 Offset tolerance model of a support plate

由模型易知，在此种情况下支撑板质量m4未发生改变，仅改变了质心偏移距离e4，故支撑板偏斜公差引起的单个不平衡量UD为

将10 块支撑板进行矢量叠加，可得到总体不平衡量UD,max为

式中α为相邻的两筋板之间的夹角。

所有支撑板因偏移产生最大不平衡量UD,max的方向 φD为

1.5 槽对称度公差模型

槽对称度为支架外环任一槽底面到支架外环中心距离同对面180°位置的槽至中心距离的差值，由于永磁体安装在转子支架外环上的槽里，控制槽对称度可使永磁体同定子之间形成的磁场均匀，使转子因磁场拉力所受的振动得以抑制[18]。实际测量时，通常选取槽底面最高点位置进行比对。假设支架外环槽底面尺寸均相同，可将槽对称度视为一个径向截面的圆的跳动，将两半圆分别向内、外偏离公差d5/2，粗实线为实际表面，虚线为理想表面，等效加工精度模型如图5 所示。

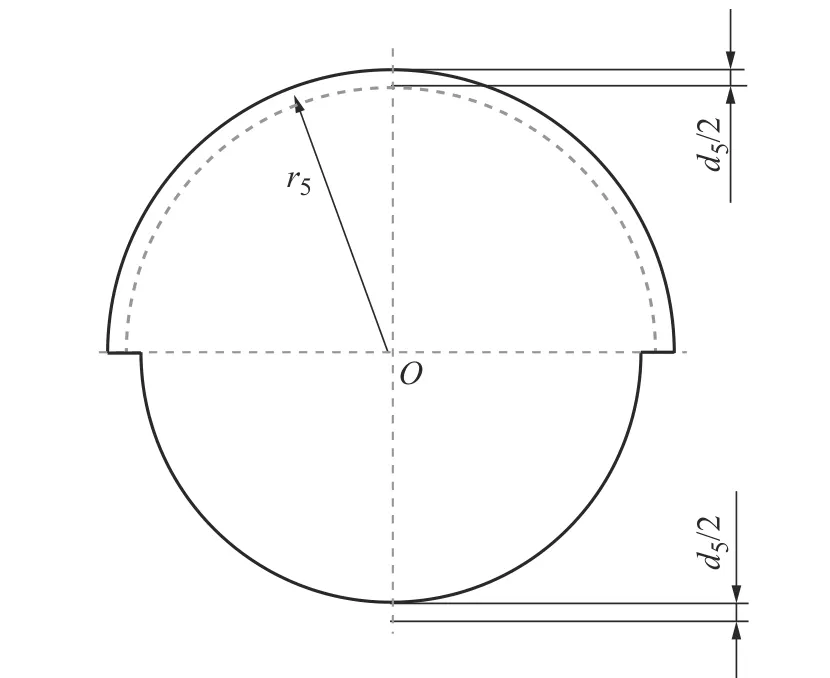
图5 槽对称度加工精度模型Fig.5 Symmetrical machining accuracy model of a slot

由模型可知，上半圆半径为r5+d5/2，下半圆半径为r5-d5/2。故因加工误差所去除的面积SS为

式中：r5为槽底面至回转中心的半径；d5为槽对称度公差允许最大值。

设槽长度为l，由此可得到此种加工误差所引起的最大不平衡量US为

式中m5为支架外环质量。不平衡量的方向为质量缺失的垂直方向。

2 永磁电机转子振动响应分析

2.1 加工精度等级对不平衡量的影响

根据工程图建立三维物理模型，核动力潜艇推进永磁电机转子模型如图6 所示。

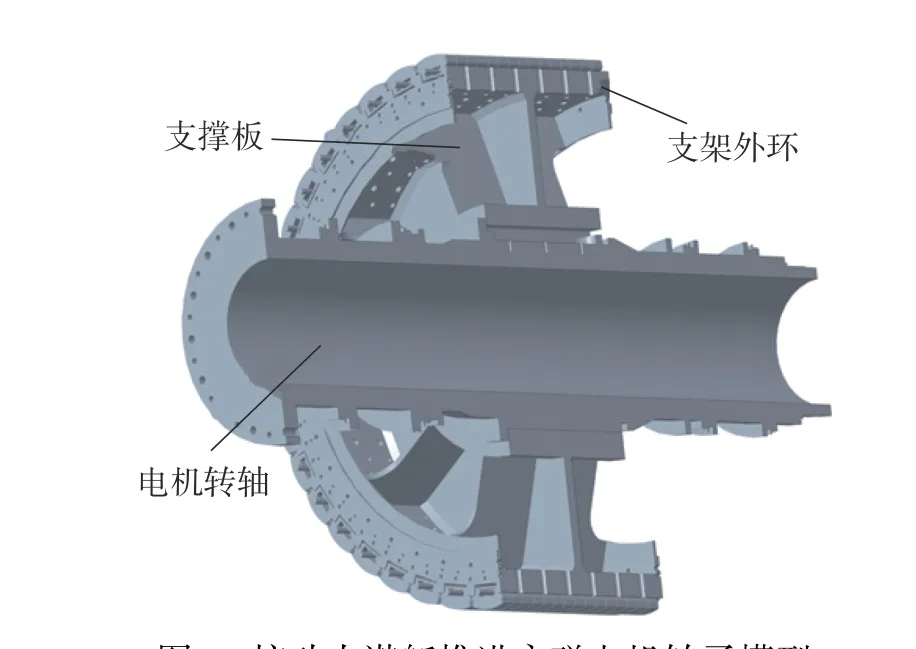
图6 核动力潜艇推进永磁电机转子模型Fig.6 Rotor model of nuclear power submarine propulsion permanent magnet motor

根据实际中使用的加工精度，将5 种典型加工工艺统一设置一个标准公差值，并以标准公差值为基准，取0.5 倍、2 倍、3 倍、4 倍公差值，共5 组公差值进行计算，具体取数为：0.025、0.05、0.1、0.15、0.2 mm。将相应的尺寸参数代入关系式中，分别得到不同加工工艺下不同加工精度引起的结构不平衡量，加工工艺对应的结构不平衡量如图7 所示。

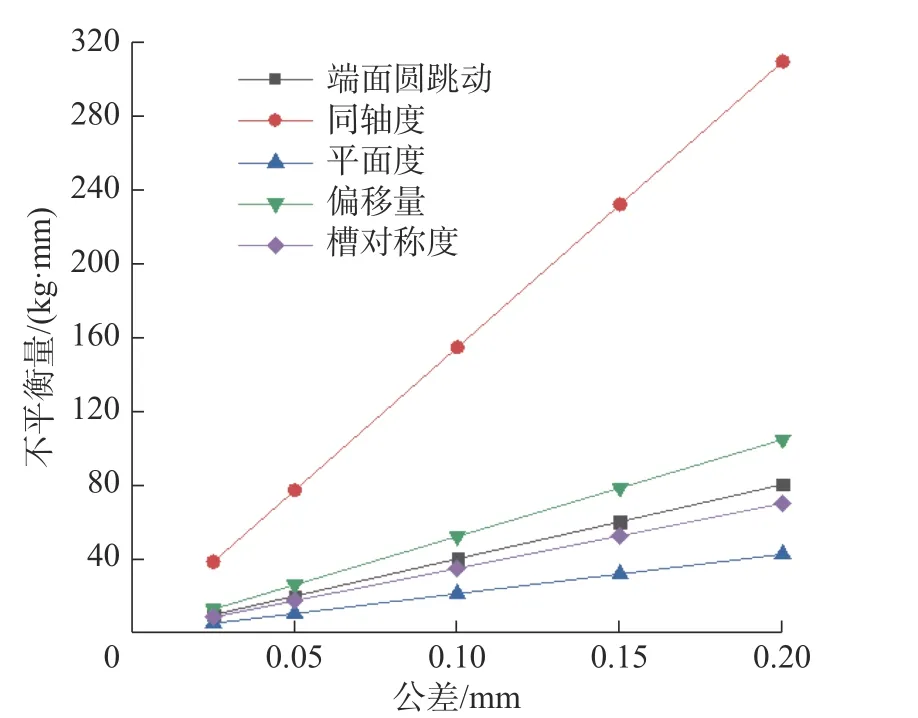
图7 不同加工工艺及其精度对应的不平衡量Fig.7 Unbalance values corresponding to different machining processes and accuracy

由图7 各个加工工艺精度等级所对应的不平衡量可知，加工精度从0.05 mm 扩大至0.2 mm，不平衡量随着公差值增大而增大，但不同种类的结构不平衡量增长幅度不同，其中以电机转轴同轴度增长幅度最大，其次为支撑板偏移量；槽对称度和端面平面度增幅最少。

2.2 加工精度等级对振动响应的影响

根据电机转子结构图，采用有限元法[19]，构建电机转子动力学有限元模型如图8 所示。

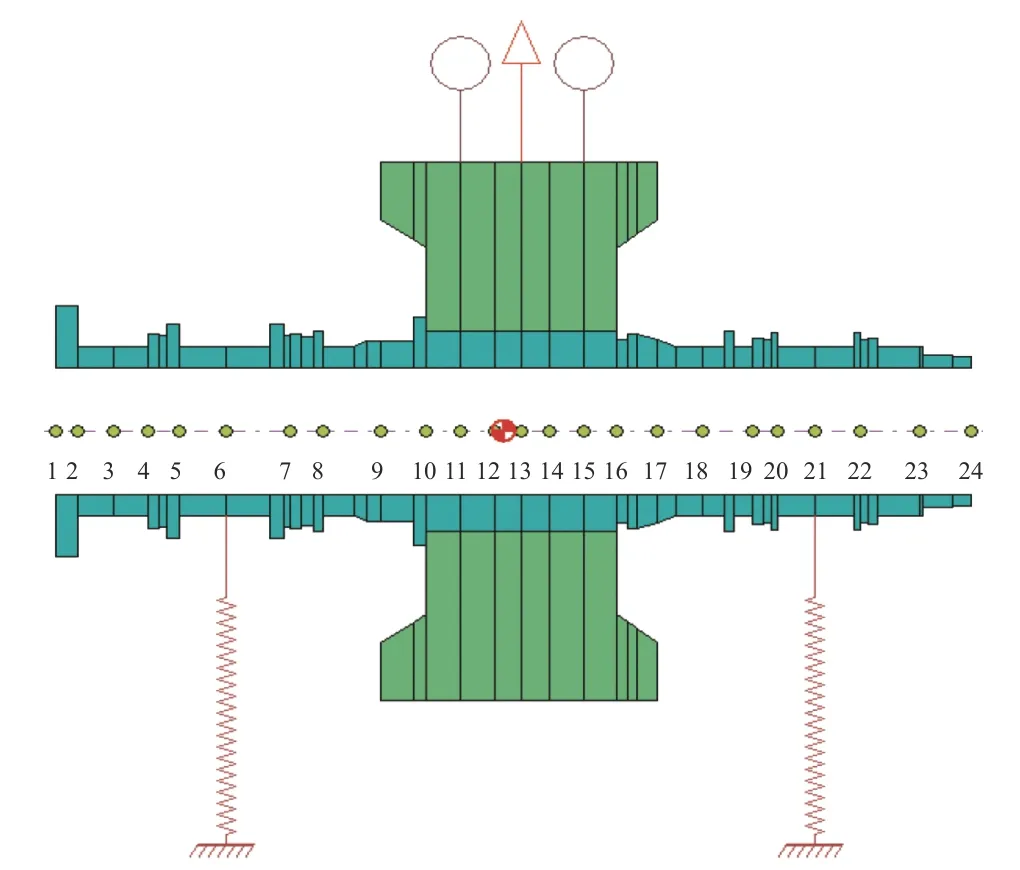
图8 电机转子动力学有限元模型Fig.8 Rotor dynamics finite element model of motor

通过对永磁电机转子进行固有频率计算，解得其一阶临界转速为5 271 r/min，模态为刚体模态，说明动力系统在89 r/min 低速巡航下，电机转子转轴整体几乎不发生挠曲变形，减少其他因素对降振方法的影响。1 阶振型及临界转速（5 271 r/min）如图9 所示。

图9 1 阶振型及临界转速（5 271 r/min）Fig.9 1 order mode and critical speed (5 271 r/min)

振动响应不仅仅和不平衡量大小有关，同时还受不平衡量所在位置有关[20]。通过三维模型可知：轴颈圆跳动产生的不平衡作用在轴颈端面上；同轴度产生的不平衡作用在轴表面上；平面度产生的不平衡作用在轴端面上；支撑板偏移量产生的不平衡作用在支架上；槽对称度产生的不平衡作用在支架外环表面上，5 种典型加工工艺对应的回转半径如表1 所示。

表1 5 种典型加工工艺对应的回转半径Tab.1 Rotation radius of 5 typical machining processes

基于电机转子-滑动轴承系统动力学模型，通过在转子相应位置施加各加工工艺导致的不平衡量激励，进行稳态同步响应分析，得到5 种典型加工工艺在轴承处89 r/min 转速点的振动幅值，其结果如图10所示。

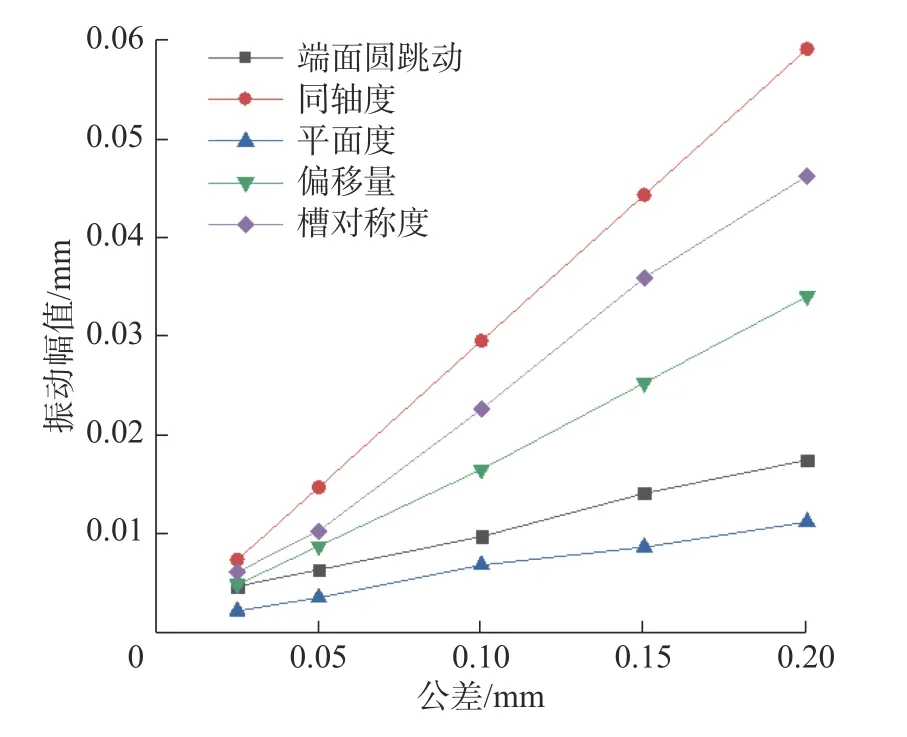
图10 转速89 r/min 时轴承处振动幅值Fig.10 Bearing vibration amplitude at 89 r/min

通过图7 和图10 对比可知，槽对称度产生的不平衡量级比支撑板偏移量产生的不平衡量级约小46%，但由于振动响应幅值受不平衡作用位置的影响，槽对称度产生的振动幅值比支撑板偏移量产生的振动幅值约大65%，说明不平衡作用位置对振动响应幅值大小有影响。从稳态同步响应分析得出转子的振动响应幅值可知：对于某核动力潜艇永磁电机转子振动影响最大的加工工艺为转轴同轴度，其次为永磁体安装槽对称度；轴颈端面圆跳动以及转轴端面平面度对振动响应影响较小。因此，提高同轴度、槽对称度的加工精度等级，可明显降低电机转子系统振幅；而提高端面圆跳动、平面度的加工精度等级，相对而言降幅效果不明显。

3 结论

1） 针对低速永磁电机转子结构振动问题，本文从加工工艺精度等级的角度，提出一种控制转子结构不平衡振动响应法。根据某核动力潜艇推进永磁电机转子实际加工情况，结合不同加工精度等级下公差范围，建立五种典型加工精度数学模型，分析加工精度对结构不平衡的影响，得出该永磁电机转子加工精度等级与转子结构不平衡量之间的内在关联。

2） 以在永磁电机低速巡航工况为例，通过构建不同加工精度等级下电机转子动力学有限元模型，分析不平衡激励下稳态同步响应，发现对该永磁电机转子振动响应影响最大的加工精度为电机转轴同轴度。

3） 在满足转子零部件装配精度需求以及性能要求的前提下，可通过优化转子加工工艺精度等级来控制永磁电机转子结构不平衡振动。后续还需进一步考虑转子零部件装配要求、加工成本等多因素的影响，通过多目标优化方法，以确定这类转子零部件加工精度的最佳等级，实现转子的低振动、高性能和低成本需求。