数值模拟技术在输气站区域阴极保护设计的应用

延旭博

（河北省天然气有限责任公司，河北 石家庄 050000）

0 引言

近年来，随着天然气行业的发展，长距离、大口径管道建设的加快，输气站区域阴极保护设计越来越受到重视。数值模拟技术为区域阴极保护设计提供了更加精确和可靠的手段，特别是在解决复杂接地系统和多回路间的干扰和屏蔽问题方面[1]，其具有传统的理论计算不能比拟的优势。与传统的经验设计、理论计算等方法相比，数值模拟的方法能够在设计阶段就预测阴极保护系统保护效果，并通过调整辅助阳极位置与数量，使阴极保护电位分布均匀，避免过保护和欠保护现象的发生[2]。在已运行多年的站场追加区域阴极保护措施的实践证明，通过数值模拟技术对阳极布置进行优化，提升了阴极保护系统的合格率，数值模拟计算的结果与现场实施后实测值误差很小。

1 数值模拟技术及其在阴极保护应用

1.1 数值模拟技术简介

数值模拟技术是借助于电子计算机，并与有限元、有限体积等相关的概念相结合，利用数值计算、图像展示等手段，实现对工程、物理、甚至是自然界中各种问题的研究[3]。最早在1953年， Bruce和 Peaceman首次对一维气体非稳态的径向和线性流动进行了数值模拟。近年来，通过与电化学技术结合，数值模拟技术在阴极保护领域得到了广泛应用，包括有限差分法、有限元法和边界元法等[4]，其中有限元法已成为复杂结构和工况下阴极保护设计最有效的手段之一。

1.2 数值模拟技术的优劣势

首先，数值模拟技术具有高精度、高效率的特点。通过数值模拟技术，可以精确计算复杂结构下的电场分布、电位分布等电化学参数[5]。此外，在模拟大型金属结构时，传统的试验方法如馈电试验需要大量的人力和时间，而有数值模拟技术则可以节省大量的资源。

其次，数值模拟技术具有较强的可视化和预测能力。在仿真过程中，可以对各种参数的变化进行实时监控和可视化展示，使得研究者可以更好地了解电化学行为[6]。此外，在设计阴极保护方案时，可以进行多种方案的仿真比较，并根据仿真结果进行优化。

然而，数值模拟技术在应用中也存在一些局限性。首先，仿真结果的准确性受多种因素的影响，如模型的准确性、边界条件准确性、物理参数的选择等。在趋于极端条件下的仿真中，由于模型的复杂性和数值计算的稳定性等问题，仿真结果可能存在一定的误差，即过拟合问题[7]。此外，诸如电解质浓度、材料特性、电极安装位置等方面的参数变化可能会导致仿真结果的偏差，需要在实际应用中不断校准、修正模型，提高其精度和可靠性[8]。同时，数值模拟仿真技术在计算效率和资源消耗方面也存在一定的问题，虽然提高网格密度可以提高计算的准确性，但会增加计算资源的消耗，因此，需要考虑计算复杂度和计算资源的平衡利用问题。

在实际应用中，需要充分考虑仿真技术的优势和局限性，并结合实际情况进行综合分析，才能更好地应用该技术。

1.3 数值模拟技术的在阴极保护的应用

传统的阴极保护设计方法依赖于现场试验以及经验公式，其考虑的影响因素有限，其设计结果往往不够精确可靠，同时也无法提供全面的阴极保护信息。相比之下，数值仿真技术以其精确性、可靠性和全面性受到越来越多的关注和应用。

在输气站阴极保护设计中，数值仿真技术能够快速准确地计算阴极保护电位分布及其对于被保护物质的保护能力。根据导电体与周围电解质的不同特性建立的有限元模型可以准确地模拟阴极保护系统的电场分布和电流密度分布。针对输气站阴极保护设计中的不同材料、不同工况、不同电解质浓度等因素进行仿真分析，可以得到相应的模拟结果，用于指导阴极保护策略的制定，提高阴极保护的精度和实用性。

利用有限元仿真技术进行输气站阴极保护设计分析，不仅可以提高阴极保护系统的设计效率，还可以降低设计成本和改进技术方案[9]。此外，模拟过程还可以对阴极保护参数进行优化设计和调整，提供更加精确的阴极保护措施，满足不同工况下的阴极保护需求[10]。

2 数值模拟在输气站X区域阴极保护设计的应用

2.1 调研输气站基本情况

在进行输气站区域阴极保护系统设计前，调研输气站X的站场平面图、埋地管道分布及尺寸、接地分布及尺寸、土壤电阻率数据和馈电实验数据等基础资料。

其中，站场平面图和埋地管道分布及尺寸、接地分布及尺寸采用查阅设计图纸资料，结合现场开挖验证的方法，以图纸资料为基础，同时对接地等进行小规模的开挖，验证图纸的准确性。土壤电阻率采用ZC-8接地电阻测量仪实地测量并记录。馈电试验即采用临时性阴极保护系统（临时电源和阳极地床）对拟保护对象进行通电极化试验，在此基础上获得不同区域的保护电流需求，并对比不同区域保护的难易。馈电试验部分数据如表1所示。

通过对该输气站进行馈电试验，实际测试电位97处，各测试点的电位分布有很大差异，在试验条件下部分测试点的阴极保护电位在有效范围的边界，证明了区域阴极保护系统的复杂性和电流分布的不均匀性。

2.2 输气站X埋地管道三维模型建立

在输气站X基础资料调研总结基础上，利用阴极保护数值模拟计算软件进行了站内埋地金属结构物区域阴极保护数值模拟计算三维几何模型，如图1所示，并进行了数值计算网格划分。

图1 输气站X几何模型

2.3 确定边界条件

边界条件的准确性直接影响数值模拟仿真结果的准确性。虽然进行了详细的现场调研，但是在模型的边界条件中，仍有一定的数据是无法精准获得的。

（1）因施工过程的不可知、不可控，接地系统在地下的分布和走向是无法全部通过开挖验证和图纸确定，因此，接地系统的规模、分布等会存在误差；

（2）土壤电阻率的分布是不均匀的，由于模型及计算机的算力限制，因此将土壤电阻率取多个测试点的平均值，因此，其对计算结果会有一定的影响；

（3）土壤的温度、含水量等其他边界条件均会影响计算的结果。

为此，利用现场馈电试验数据，通过反演计算来优化不同区域埋地管道的阴极边界条件。通过调整埋地管道的阴极边界条件，并与馈电试验的数据进行对比，得到与实际测试数据误差最小的边界条件作为埋地管道的阴极边界条件。表2为部分管道反演结果及其与实际馈电结果的对比。

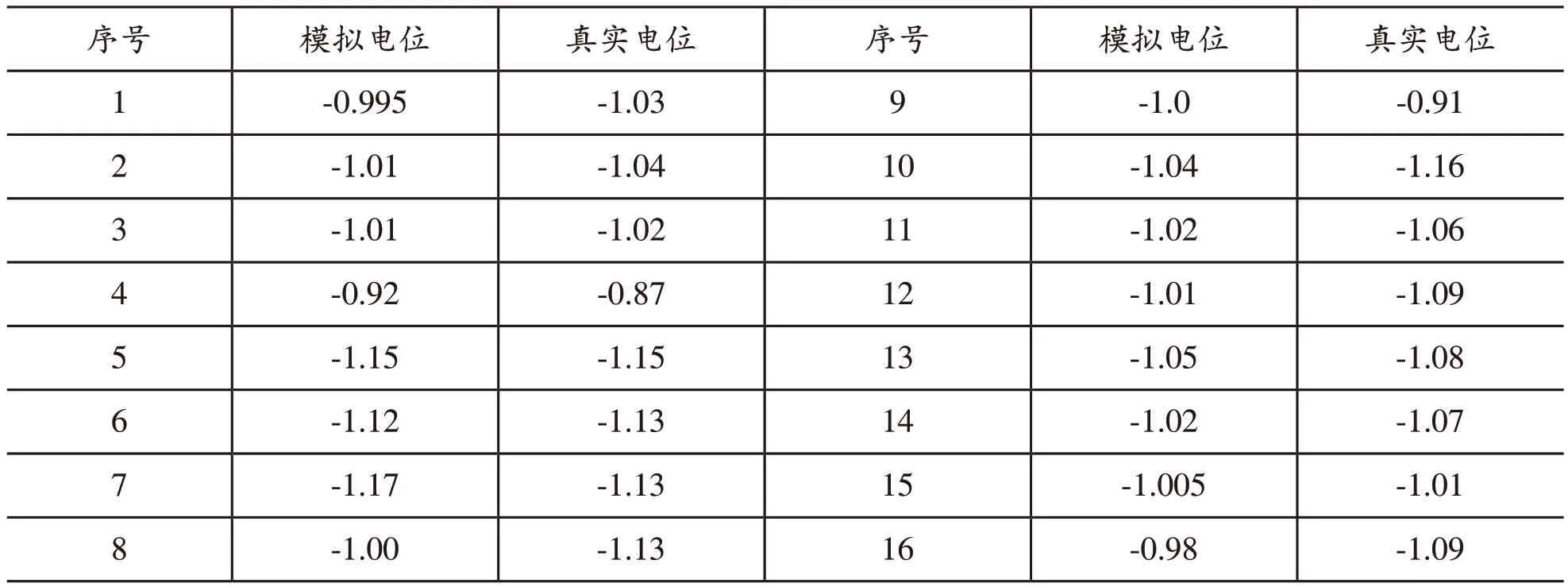
表2 模拟电位与真实电位对比

由对比结果可见，计算结果与实测结果基本吻合，相对误差基本控制在10%以内，说明反演获得的管道边界条件可以反映实际情况。

3 极地床分布方案优化

在基于馈电试验获得的各区域埋地管道阴极边界条件基础上，对不同区域阳极地床分布进行了优化计算，重点是阴极保护电位在合格范围边缘的1#、2#及3#区域，其分布如图2所示。

图2 阳极分布优化重点区域

对1#区域，调整1#阳极地床的位置与输出电流，经调整后其电流从5.0A降至3.0A，与附近管道最近距离为13m；优化后该区域内所有埋地管道极化电位均落于-850～-1200mV（CSE）范围内，全部得到了理想的保护。

对2#区域，调整2#阳极地床的位置，位置调整为距离上方管线7m，距离左侧管线5m，同时新设置了5#阳极地床，距离最近管道3m。经过阳极地床位置及数量优化后，该区域内埋地管道极化电位均落入-850～-1200mV（CSE）范围内，全部得到了理想的保护。

对3#区域阳极地床的位置及数量进行优化，新增6#阳极地床，该地床与附近管道的最近距离为8m。经过阳极参数优化，3#区域的埋地管道极化电位均落入-850～-1200mV（CSE）范围内，全部得到了理想的保护。

优化后的阳极分布如图3所示。

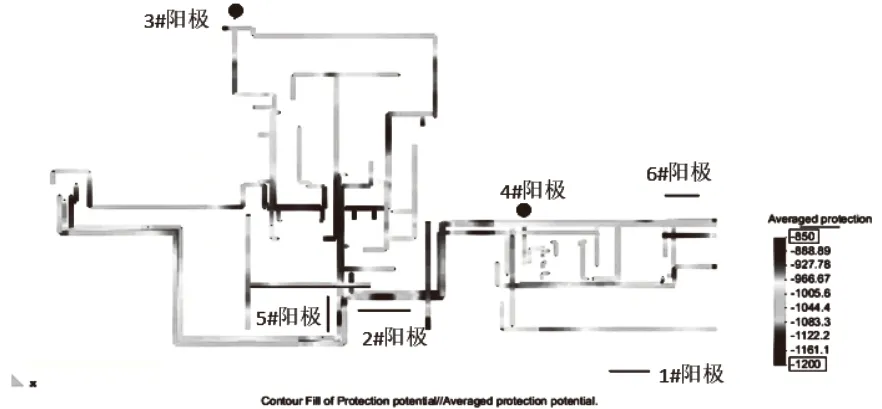
图3 优化后的阳极分布

4 应用效果与分析

4.1 数值仿真计算结果验证

项目按优化后设计投用后，每回路输出电流2～3A，与数值仿真结果一致。经密间隔电位测试，阴极保护电位全部在-0.85～-1.25V有效保护范围内，且与数值仿真结果误差均在10%以内，验证了仿真计算的准确性。

4.2 应用展望

数值模拟技术可以在输气站区域阴极保护设计中快速准确地模拟电位分布情况等关键参数，从而能够对阴极保护方案进行优化。经过实际应用验证，该方法能够显著提高阴极保护效果，为阴极保护设计提供了有益的帮助。未来可以结合更多的实际应用情况，提出更加优化的阴极保护设计方案，从而更好地保护输气站区域设施的安全稳定运行。