静态直流杂散电流对埋地金属管道干扰规律数值模拟

田海州 郭小东 黎少飞 杨 鑫 林海峰 祁贵宏 刘天慧

（1. 国家管网集团西南管道有限责任公司天水输油气分公司，甘肃 天水 741002；2. 国家管网集团油气调控中心，北京 100013）

0 引言

随着中国经济迅速飞起，各行各业对能源需求的日益趋增，由于金属管道在长距离输送方面，具有输送远、数量大、效率高、成本低及稳定好等特点被广泛应用于能源输送领域[1]。截止2021年底，我国就油气长输金属管道总里程累计达到15万km[2]。但由于考虑地形限制设计因素、公共走廊紧缺、埋地金属管道选址相似等原因，两者的交叉、并行情形不可避免[3]。在实际工程中，埋地金属管道最常用的防腐技术是阴极保护和保护涂层[4]。阴极保护系统虽然可减少涂层失效处管道钢的化学降解，但外加电流阴极保护（ICCP）系统的静态直流杂散电流可能会在一定范围内对交叉管道造成干扰腐蚀[5,6]。随着电化学理论和计算机技术的发展，数值模拟方法已被证明是研究阴极系统和管道杂散电流腐蚀有效和有力的工具[7]。其中用于杂散电流数值模拟干扰腐蚀研究方法主要有有限差分法（FDM）、有限元法（FEM）和边界元法（BEM）[8]。BEM与其它两种方法相比计算简便、模型简化和迭代次数少等优点被广泛应用[9]。Gadala等[10]利用Matlab编程工具，计算了长输管道的阴极保护电位分布，并通过实验数据得到验证实验。Liu[11]等使用BEASY模拟对石油钻井平台的应用阴极保护得出平台表面的阳极分布和电势分布。在此基础上，Metwally等[12]利用数值模拟研究了埋地金属管道受静态直流杂散电流在阳极干扰、阴极干扰和诱导干扰下的干扰腐蚀程度。Gui[13]等人利用 BEASY研究了交叉角、两条管道的距离、阳极输出电流、土壤电阻率对阴极保护系统中静态直流杂散电流的干扰腐蚀效应。Yang[14]等人利用COMSOL模拟软件研究了阴极保护系统中静态直流杂散电流受常见各种因素影响下的电极电势变化规律，但并未考虑涂层电导率及厚度等对干扰管道杂散电流密度影响的直接评价指标。目前有关埋地管道受静态直流杂散电流干扰程度相关问题的直接评价研究尚不充分，并未提出有效合理建议。

本文利用COMSOL软件电化学模块中电流分布边界元接口对电流密度强大的敏感性，建立了强制电流阴极保护系统中静态直流杂散电流对交叉受干扰管道的模型，对影响干扰管道杂散电流密度的主要因素包括交叉角、阳极与交叉点距离、土壤电导率、防腐涂层厚度进行了深入研究和分析，从而得到一些可用的结果为管道现场施工、运行及防护提供理论指导和现场参考。

1 模型建立

1.1 几何模型

采用COMSOL软件开展计算研究。该软件电化学模块中以边界元技术的求解组为基础，通过构建三维几何模型、设置材料、给定边界条件及划分边界网格，迭代法计算模型内各个结构和位置处的土壤中介质电流密度分布。

由于实际工程中外加电流阴极保护系统中辅助阳极与保护管道距离较远，保护管道与干扰管道也很长，因此，可将辅助阳极对干扰管道的干扰可以简化成集中激励电流源，计算过程中将管道和辅助阳极统一简化为直线结构，计算模型由保护管道、受干扰管道和阳极组成如图1所示：保护管道和干扰管道长30km，二者在中点以90°相互交叉。保护管线取中贵天然气管道直径为1016 mm，其通常采用外加电流的阴极保护方式，干扰管线取宁夏清水河的输水管道直径为700m，其一般无需阴极保护只采用防腐涂层保护方式，阳极直径为0.1m，高度为5m，距与受保护的管道100m，距两管道交叉点15km，如图1所示。

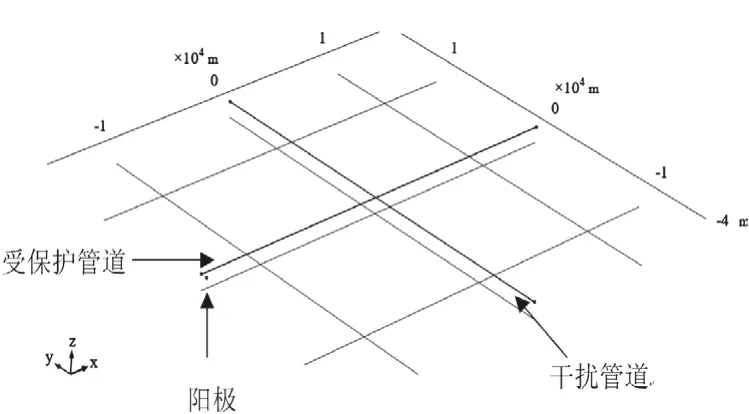
图1 计算模型示意图

1.2 控制方程和边界条件

对于受干扰管道是边缘电极，可以根据电流分布，边界元接口求解边缘区域上的电解质电势和电流密度，根据：

其中i1是电解液电流密，单位为A/m2；σ是土壤电导率，单位为 S/m。

在辅助阳极边缘，使用电解液电流密度节点规定外加电流密度，如下所示：

其中n是法向量，指向域外；i2为辅助阳极边缘的电流密度，单位为A/m2。

在受干扰的管道上，使用边缘电极节点规定电化学反应动力学，如下所示：

其中f（φ）是用传统的三电极电池组件测量埋地管道x80钢的极化曲线数据的插值函数，如图2所示。

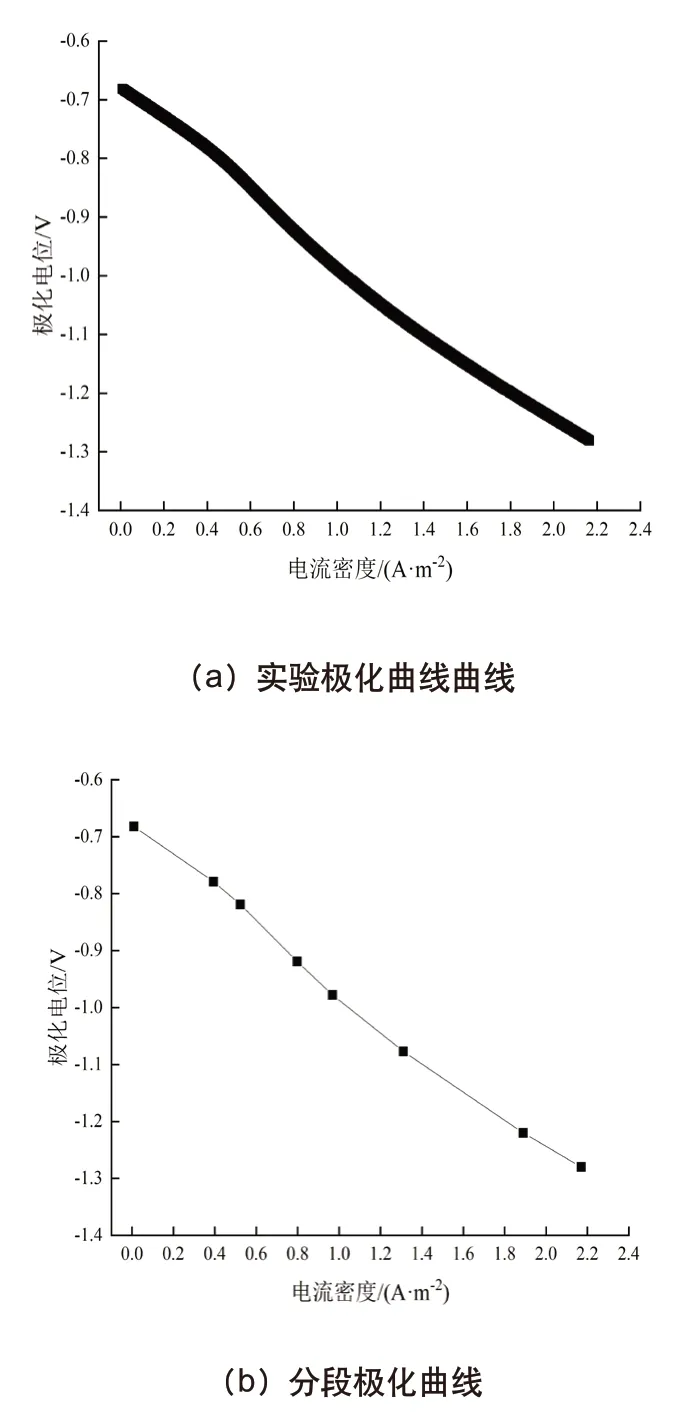
图2 极化曲线

图2（a）的极化曲线用作埋地管线的边界条件，但它是一条非线性曲线，因此必须以分段线性插值方法使用极化数据，如图2（b）所示。对于干扰管道，将电位模型设置为零外加电流的浮动电位，表明干扰管道不与任何物体电连接，仅通过管道表面发生的电化学反应与相邻土壤区域发生相互作用。根据辅助阳极的外加电流密度即可求出干扰管道上的杂散电流密度。

1.3 模型求解

根据1.1节中中贵天然气管线和宁夏清水河输水管线的现场穿越工况建立强制电流阴极保护系统对埋地金属管道干扰模型，选取现场工况相关参数（如表1所示）并求解，具体步骤如下：

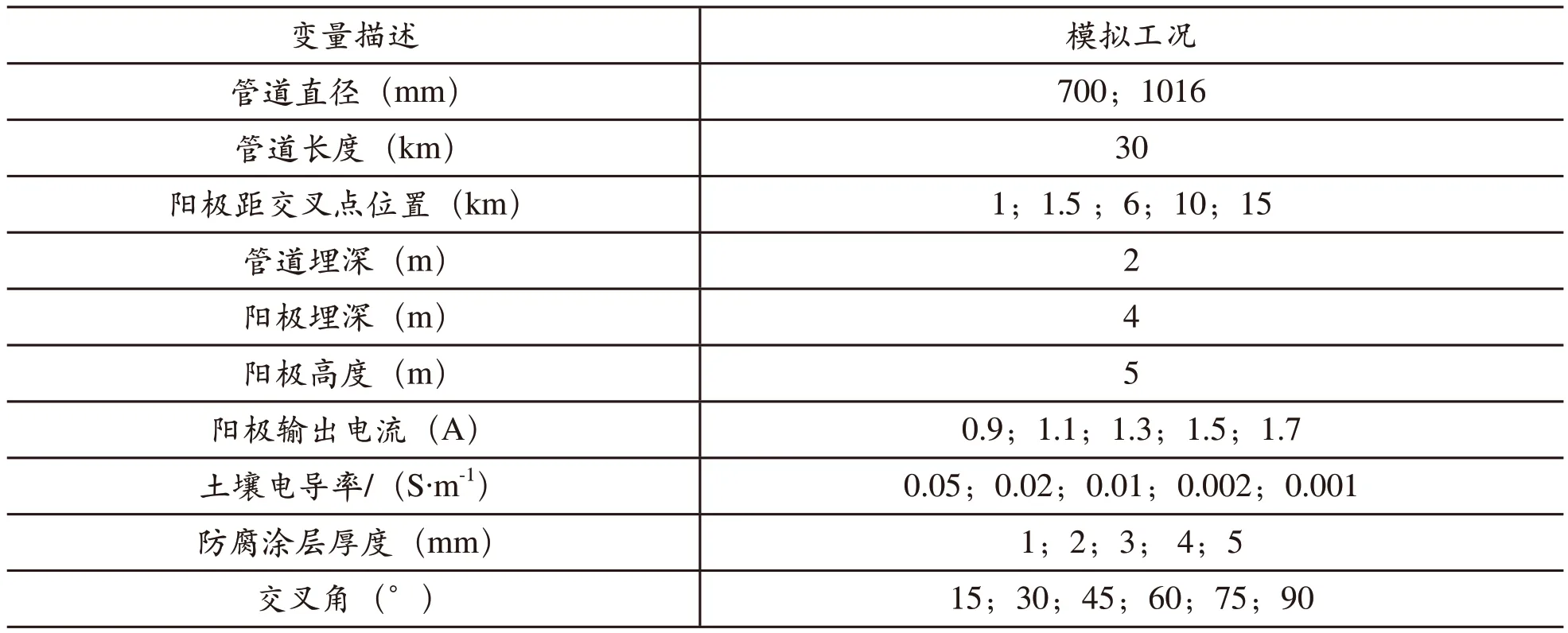
表1 静态直流杂散电流干扰模拟工况

（1）网格剖分，采用用户控制，选取最大单元格为8m，依次对阳极、保护管道和干扰管道进网格刨分；

（2）求解器设置，设置稳态求解器精度不超过0.001，直到模拟数值结果数据精度满足系统要求；

（3）后处理，利用软件自带的作图进行相关分析和后处理工作。

1.4 模型验证

文献[13]通过搭建小型实验模型对受阴极保护系统中静态直流杂散电流干扰的管道电位进行实验检测，本文分别选取干扰管道-1m和-0.5m、0m、0.5m及1m位置电位进行模型验证。保持模型设置的计算参数与文献[13]一致，模拟结果与实际测量数据（如表2所示）。

表2 模型验证结果

由表3可知，现场实测数据与模拟结果之间的误差小于3%。因此，本文模型可用于后续研究。

2 结果与讨论

2.1 杂散电流密度分布

设定外加电流阴极保护系统中静态直流杂散电流对干扰计算模型中，土壤电导率为0.001S/m，防腐涂层电导率为1×10-5S/m，阳极与交叉点距离为15km，交叉角为90°，保护管道直径为1016mm，干扰管道直径为700mm，其它参数如表1所示，模拟得到沿干扰管道杂散电流密度分布如图3所示。

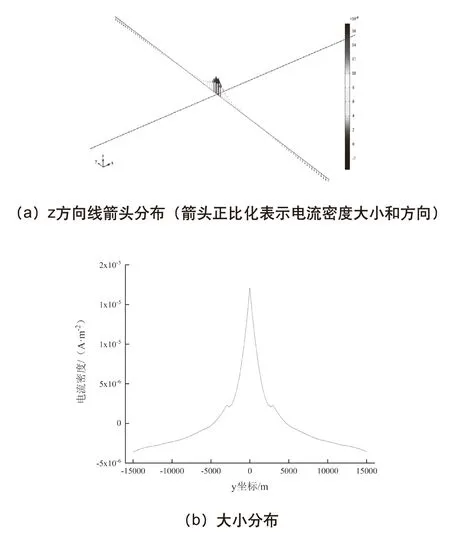
图3 干扰管道杂散电流密度密度分布

在图3中，由于阳极埋深大于干扰管道，故规定沿管道z方向向上的杂散电流密度数值为正，表示杂散电流通过土壤介质流入干扰管道；而规定沿管道z方向向下杂散电流密度数值为负，表示杂散电流通过干扰管道流回土壤。由图3（a）可知，沿干扰管道杂散电流密度箭头流向从交叉点流入依次向两端先依次减小至零后再向流出逐渐增大，且分别在交叉点达到流入的最大值和两端达到流出的最大值。依图3（b）得，沿管线杂散电流密度分布与图3（a）有着相似的分布规律，即从交叉点流入达到最大值后依次向两端减小至零，再流出逐渐递增至最大；由于金属管道内无电荷积累，依据电流连续性方程可知，干扰管道的杂散电流密度分布曲线与电流密度为零（图中红色点划线）围成图形正面积（流入电流量）等于其围成图形负面积之和（流出电流量）。

2.2 交叉角的影响

仅改变两管道的交叉角，保持其它参数与2.1节中计算模型一致（下同），得到不同交叉角下管道杂散电流密度峰值分布如图4所示。

由图4计算结果可知：当两管道交叉角在15～90°范围时，随着交叉角的减小，干扰管道的杂散电流密度峰值依次迅速升高，其所受干扰也越强，且干扰递增程度愈来俞强。当交叉角为60～90°时，其变化对干扰管道杂散电流密度峰值的影响较小，管道所受干扰影响减小；而当交叉角为15～45°时，其变化对干扰管道杂散电流密度峰值的影响较大，管道所受干扰影响增强。因此，实际工程中当两管道交叉不可避免时，应尽量控制其交叉角大于60°。

2.3 阳极与交叉点距离的影响

保持其它参数不变，仅改变阳极与交叉点的距离，得到不同距离下干扰管道杂散电流密度峰值分布如图5所示。

图5 阳极与交叉点距离对干扰管道杂散电流密度影响

由图5计算结果可得：随着阳极与交叉点的距离减小，干扰管道的杂散电流密度峰值依次迅速升高，其所受干扰也越大，且干扰递增程度愈来愈烈。当与交叉点距离为1～6km范围时，其变化对干扰管道杂散电流密度峰值的影响较大，管道所受干扰的影响增强；而当与交叉点距离为6～15km时，其变化对干扰管道杂散电流密度峰值的影响较小，管道所受干扰影响减弱。因此，实际工程中当两管道交叉不可避免时，应着重考虑辅助阳极的位置，应避开其与两管道交叉点小于6km的不利位置。

2.4 土壤电导率的影响

保持其它参数不变，仅改变土壤电导率的大小，得到不同电导率下干扰管道杂散电流密度峰值分布影响如图6所示。

由图6计算结果可知：随着土壤电导率的减小，干扰管道的杂散电流密度峰值均依次升高，其所受干扰越大，且干扰递增程度逐渐增强。这是由于流入土壤中总电流密度不变，而流入干扰管道处杂散电流密度大小与其周围土壤电导率有关，即干扰管道周围土壤电导率越大，流入土壤的电流就会增加，而流进干扰管道的杂散电流密度反而会减少。当土壤电导率在0.05～0.01S/m时，其变化对干扰管道杂散电流密度峰值的影响较小，管道所受干扰影响也变弱；而当土壤电导率在0.01～0.001S/m时，其变化对干扰管道的杂散电流密度峰值影响较大，管道所受干扰影响也增强。因此在实际工程中，两管道交叉不可避免时，应尽量将其交叉点设在土壤电导率较大的区段。

2.5 防腐涂层厚度的影响

管道随着投产年限的增加难免会由于第三方施工或机械损伤等造成防腐涂层变薄、破损等情况，此时我们可通过改变防腐涂层厚度变化进行模拟。保持其它参数不变，仅改变防腐涂层厚度，得到不同涂层厚度下干扰管道杂散电流密度峰值分布如图7所示。

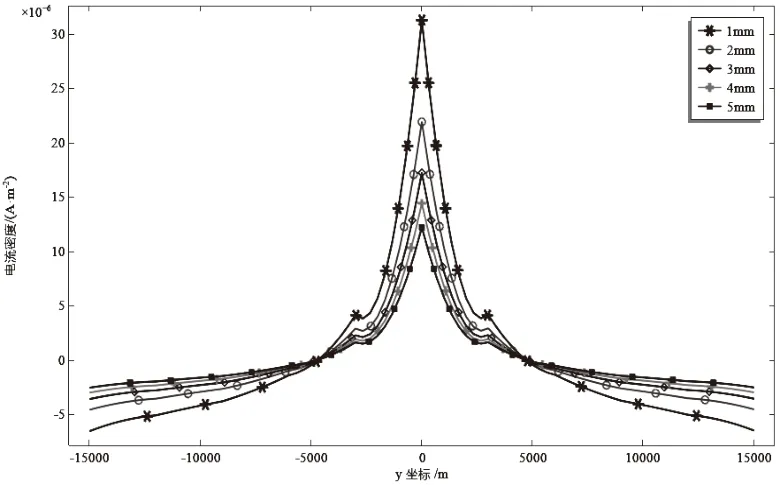
图7 防腐涂层厚度对干扰管道杂散电流密度影响

由图7可知，随着管道防腐涂层厚度的减小，受干扰管道的杂散电流密度峰值依次增大，其所受干扰也增强，且干扰递增程度愈来越明显。当涂层厚度在1～3mm时，其变化对干扰管道杂散电流密度峰值的影响较大，管道所受干扰的影响增大；而当投产时间在3～5mm时，其变化对干扰管道杂散电流密度峰值的影响较小，管道所受的干扰影响减小。因此，在实际工程两管道交叉时，应尽可能在管道投产早期对管道防腐涂定期检测，尤其对干扰管道早期发现的防腐涂层有破损情况，其破损变化情况对管道干扰影响较小，应尽早发现尽早处理。

3 结语

文中建立了考虑管道极化效应的边界元干扰模型。通过软件计算结果与实验数据结果的对比，验证了文中数值模拟的正确性。通过仿真计算，获得了几种典型干扰参数下静态直流杂散电流对干扰管道的干扰规律，并对各种因素影响干扰的工况提出合理的建议，供实际工程参考和选用，得出如下结论：

（1）阳极与交叉点的距离对干扰管道杂散电流密度分布的影响最大，与交叉点距离越小，干扰管道杂散电流密度峰值越高，其所受干扰也越强；尤其当距离小于6km时，其干扰是其它因素的几倍，应在实际工程中尽量选取辅助阳极与交叉点大于6km的位置；

（2）交叉角、土壤电导率及防腐涂层厚度对干扰管道杂散电流密度分布的影响显著，交叉角（15～90°）、土壤电导率及涂层厚度越小，干扰管道杂散电流密度峰值越高，其所受扰程度越强；尤其当交叉角小于45°、土壤电导率小于0.01S/m及防腐涂层厚度小于3mm时，其变化对管道干扰影响显著增强，应引起足够重视，尽量避开其相应的不利交叉角位置和土壤地区以及尽早对防腐涂层厚度变化进行处理。