Insight into the magnetic behavior and magnetocaloric effect of a borophene monolayer

Ying An ,Wei Wang,* ,Bo-wen Xiao ,Si-yu Huang and Zhen-yao Xu

1 School of Science,Shenyang University of Technology,Shenyang 110870,China

2 School of Electrical Engineering,Shenyang University of Technology,Shenyang,110870,China

Abstract The successful discovery of borophene has opened a new door for the development of 2D materials.Due to its excellent chemical,electronic and thermal properties,borophene has shown considerable potential in supercapacitors,hydrogen storage and batteries.In this paper,the thermodynamic characteristics and magnetocaloric effect of borophene are specifically studied using the Monte Carlo method.We find that there is an opposite impact between the spin quantum number and the crystal field on the magnetization,magnetic susceptibility,specific heat and magnetic entropy of the system.Moreover,increasing the spin quantum number or decreasing the absolute value of the crystal field can improve the relative cooling power,the coercivity (hc),and the remanence (MR) and the area of the loop.

Keywords: borophene monolayer,Ising model,magnetic behavior,magnetocaloric effect,Monte Carlo method

1.Introduction

In recent years,a number of 2D materials have been successfully discovered in succession,such as stanene [1],silicene [2,3] and transition metal dichalcogenides [4,5].To date,due to its high anisotropy,and the unique and adjustable physical and chemical properties of borophene,it has attracted extensive attention of researchers [6–9].In 2014,Piazza et al discovered for the first time through experimentation that it is possible to create single atomic layer boron sheets with hexagonal vacancies [10].The results of this experiment indicated that B36can be regarded as the minimum unit for the construction of the structure of 2D monolayer α-phase borophene,and thus presented the concept of borophene.In an ultra-high vacuum,borophene was successfully synthesized by Mannix et al on a silver surface [11].In addition,Feng et al discovered boron sheets on a single-crystal Ag (111) surface using scanning tunneling microscopy and explored the β12and χ3phases [12].

Recent advances in the theoretical studies of borophene have further pushed its development.Peng et al used firstprinciples density functional theory (DFT) to explore the electronic structure,thermodynamics and optical characteristics of the materials,confirming its excellent electrical conductivity [13].Utilizing the same method,Valadbeigi et al calculated the energy,enthalpy and Gibbs free energy of the adsorption process [14].Lopez-Bezanilla et al found that borophene can be transformed from a metal to a semiconductor using the DFT method [15].In [16],the influence of geometric orientation and edge effects on the magnetic behavior of borophene nanoribbons was calculated using the DFT method.It is noteworthy that Zou et al used relevant effective field theory (EFT) for the first time to investigate the magnetic properties of borophene structure[17].Other characteristics have also been discovered in theory,such as hyperelasticity and flexibility,and stressinduced anisotropic transformation [18–20].As a result,it has great potential to be used in a variety of applications,including sensing and bio-sensing devices [21,22],optoelectronics [23] and supercapacitors [24].

In studying the magnetic properties of borophene,the Ising model [25,26] and Monte Carlo (MC) simulations have also been extensively applied.For example,the magnetization and magnetic susceptibility behavior of a diluted core–shell borophene structure were simulated using the Monte Carlo method [27].Gao et al calculated the dynamic magnetic peculiarity of a mixed spin core–shell borophene nanoribbon structure using the same method [28].In addition,the magnetic properties of a single-spin borophene structure[29] and an ApB1-pbinary alloy borophene structure [30]were investigated by applying the same method.More importantly,Maaouni et al discussed the thermal magnetization behavior of a core–shell structure (5/2,3/2) under reduced exchange coupling interactions through Monte Carlo simulation [31].

A change in sample temperature following an adiabatic change in the applied magnetic field is known as the magnetocaloric effect (MCE),which is an inherent feature of magnetic systems [32].MCE has been extensively used in room and cryogenic temperature refrigeration applications[33,34].In recent years,many experimental studies have found that the originally non-magnetic graphene can be made magnetic by doping magnetic transition metal atoms or through their replacement [35,36].In the periodic table of elements,boron and carbon are close neighbors in that they have similar chemical properties.Therefore,borophene might also have magnetism in this way,which has been successfully discussed in theory [37].It is shown that the magnetic moment is largest when Mn atoms are embedded.The significant effects of spin quantum numbers on the magnetic and MCE characteristics of different physical systems have been revealed through recent theoretical studies.Zhang et al,using EFT [38],linear spin wave approximation and the retarded Green’s function method [39] explored the effect of the spin quantum number on the phase transition temperature of graphene-like quantum dots and the magnon energy gap of a ferro-anti-ferromagnetic multisublattice system.Similarly,utilizing the Green’s function method,Mi et al carefully calculated and analyzed the role of spin quantum number on sublattice magnetization,Nel temperature,internal energy,and free energy of frustrated spin-S J1-J2Heisenberg antiferromagnet on bcc lattice [40].In [41],the effect of spin quantum numbers (S=1/2,1,3/2,2,5/2 and 3) on magnetization,magnetic susceptibility and specific heat of Ising fullerene-like nanostructures was explored.Akıncı et al investigated the magnetocaloric properties of the spin-S Ising model on a honeycomb lattice with some spin values of S=1,3/2,2,5/2,3,7/2 using EFT [42].They found that larger spin quantum numbers can improve the cooling capacity and MCE of the system.These research results have motivated us to clarify how changes in spin quantum numbers affect the magnetism,thermodynamics and MCE of borophene monolayers.Hence,in this study,using the Monte Carlo method we explore the influence of crystal field,external magnetic field and spin quantum number on the magnetic characteristics and magnetocaloric effect of borophene structure.

2.Model and method

A single-spin Ising model of borophene monolayer containing a number of B36unit cells is shown in figure 1.We give the Hamiltonian of the system as follows:

The system was simulated using the Metropolisalgorithm Monte Carlo method [43].The periodic boundary condition was established along the 2D plane.In order to show how to choose the Monte Carlo steps (MCS) to ensure this simulation,figure 2 presents the variation of the magnetization (M) with MCS for fixed S=2,D=-0.2,h=0.5 and T=1.01.From this figure,it can be seen that the M becomes more stable after using the MCS approach,3 × 105,which indicates that the system is in equilibrium.Therefore,we abandoned the first 3 × 105MCS and retained the last 2 × 105steps to calculate the magnetic,thermodynamic quantities and MCE characteristics of the borophene monolayer.In addition,by analyzing the finite-size effect,the total number of spins in the system was also ascertained.N is defined as the number of all sublattices,namely the size of the system.The magnetic susceptibility χ of the system with spin-3/2 as a function of different sizes N is summarized in figure 3.The results indicate that the temperatures corresponding to the peak of the χ curves are invariable for N ≥1668.Thereby,the total number of spins,N=1668,was chosen to save computation time.

The formula below can be used to calculate the total magnetization of the system per site:

Thus,the magnetic susceptibility χ of the system per site is calculated by the formula:

where,β=and T and kBrepresent the absolute temperature and the Boltzmann constant,respectively.Moreover,〈...〉 is the average of the thermodynamic quantities.

The specific heat of the system per site can be obtained with the following formula:

The magnetic entropy (S) and the magnetic entropy change (-ΔSm) are calculated using the following equations:

In the formula,U represents the internal energy of the system per site as follows:

The relative cooling power (RCP) can be represented by the following equation:

where,T1and T2are low and high temperatures,respectively,which correspond to the two extremes of half of the maximum of ΔSm.

3.Simulation results and discussion

3.1.Magnetization,magnetic susceptibility,specific heat and magnetic entropy

Figure 4 illustrates how D and various spin quantum numbers affect the M of the system.Here,the five magnetization saturation values can be observed in the M curves.As can be seen from the formula (2),the saturation value of the M is similarly sensitive to the spin quantum number.More specifically,a larger spin value corresponds to a greater saturation value.All the M curves go down and fall to zero as T goes up,suggesting that the system becomes disordered.Moreover,the decreasing slope of the M curve increases with the increase in negative direction of D when the spin value is constant.Similar behavior was also revealed in magnetic nanostructures [44,45].In accordance with of the principle of minimum energy,the spins tend to be more inclined to flip in the low spin state for the larger ∣D∣ .

Figure 5 depicts variations of the χ under different spin quantum numbers and D with fixed h=0.1.From this figure,we can clearly observe that the temperature associated with the peak of the curve,namely TC,gradually rises with the spin quantum number increasing at the same D.This is consistent with the findings presented in [41].This means that larger spin quantum numbers are more conducive to the stability of the system.However,TCdecreases as ∣D∣ increases since D would damage the stability of the system,which is the opposite of the effect of spin quantum numbers.

In figure 6,it is demonstrated how D and spin quantum numbers affect the C of the borophene monolayer with fixed h=0.1.The results suggest that all the curves exhibit the same variation tendency,which is that they all rise initially to the peak and then start to decline.In addition,the influence of the spin quantum number and D on the C of the whole system is contradictory,where the peak of the C curve may move to the right under the influence of a greater spin quantum number.

Figure 7 presents the magnetic entropy S of the borophene monolayer when h=0.1.These S curves display an increasing trend as T gradually increases and achieves transitions from the ordered to the disordered state at the inflection point.Notably,the S curves move towards the hightemperature zone with the spin value increasing with fixed D.The reason for the above phenomenon is that a larger spin value can improve the chaos of the system,improving TC.Finally,the critical temperature under the influence of different spin quantum numbers is displayed in figure 8.It is obvious that TCdecreases with increasing ∣D∣ or decreasing the spin quantum numbers.

3.2.Magnetocaloric effect

Figure 9(a) shows that the relationship between -ΔSmand T is induced by various D and spin quantum numbers.When D is the same,the -ΔSmcurves shift towards the higher temperature area as the spin quantum number increases.This demonstrates that,in terms of entropy change,the stability of the system can be significantly enhanced by increasing the spin quantum number.The theoretical results are qualitatively consistent with the study of the spin-S (S ≥1) Ising model[46].However,as ∣D∣ increases,the -ΔSmcurve changes towards the low-temperature region.Either the increase in the spin quantum number or ∣D∣ decreases the maximum value of the -ΔSmcurve.Figure 9(b) exhibits the influence of D on-.It can be seen that the negative increase of D hinders the -ΔSm.The spin would flip for a stronger crystal field,so the system becomes disordered more easily,and thus undergoes phase transition more easily at low temperatures.Moreover,-decreases with increasing spin quantum number when D is constant.For example,for D=-0.1,-decreases from 0.023 to 0.010 when the spin quantum number changes from 1 to 3.The reason for the incline in the peak is that the larger spin quantum number can improve the stability of the system,as shown in figure 5.

Next,the impacts of spin quantum numbers and Δh on the -ΔSmare presented in figure 10(a).By increasing the spin quantum number from 1 to 3,the peak value of the-ΔSmcurve becomes smaller and shifts to the right.In contrast,for a fixed spin quantum number,the maximum of the -ΔSmcurve becomes larger with Δh increasing.For instance,taking S=1,the maximum value of the -ΔSmcurve increases from 0.105 to 0.377 as Δh enhances.The spins can be forced to be organized in parallel by a strong applied magnetic field.To be more precise,the magnetic entropy change might decrease when Δh increases since h is beneficial to the order of the whole system.Similar behavior has been observed in both theoretical and experimental studies of some other structures,such as perovskite ferromagnetic thin films [47],bilayer ferromagnets [48],layered perovskites [49] and nano-graphene bilayers [50].Furthermore,figure 10(b) illustrates the variation of-under various spin quantum numbers and Δh.It can be seen from the figure that each curve tends upwards as increases for the same spin value,that is,becomes larger.However,the effect of spin quantum number on-is opposite to that on Δh.Similar simulation results were also observed in the structures of both AnB60-nfullerene-like structure [51] and Ho3Pd2compound [52].In addition,by comparison with figure 9,it is found that Δh has a stronger effect on -ΔSm.

In figure 11,the impacts of Δh and T on the -ΔSmare plotted.Obviously,in the sub-figures,the -ΔSmgradually increases during the increasing process of Δh.This agrees with the findings in figure 10(a).By comparing the five subfigures,the temperature that corresponds to the maximum value of -ΔSmis observed to be moving slowly towards the high-temperature area.For example,taking S=2,the corresponding temperature range is 3.504-8.263.Nevertheless,the corresponding temperature interval changes to 5.162-16.052 when the spin quantum number increases to 3.This indicates that the heat absorption capacity of the system is continuously increasing.One can determine the optimal working temperature range for magnetic refrigeration from the magnetic entropy change.In addition,the maximum magnetic entropy change happens near the critical temperature,which should belong to the continuous second-order phase transition from order to disorder.

Figure 12 shows the variation of the -ΔSmunder the effects of Δh and T for various D with fixed S=2.As can be seen from the figure,-ΔSmalso increases with the increase in Δh.Similarly,the corresponding temperature range shifts to the right as∣D∣ increases from 0.1 to 1.6.However,it is found that the change in D has less obvious influence on -ΔSmthan the spin quantum number when comparing figure 11.

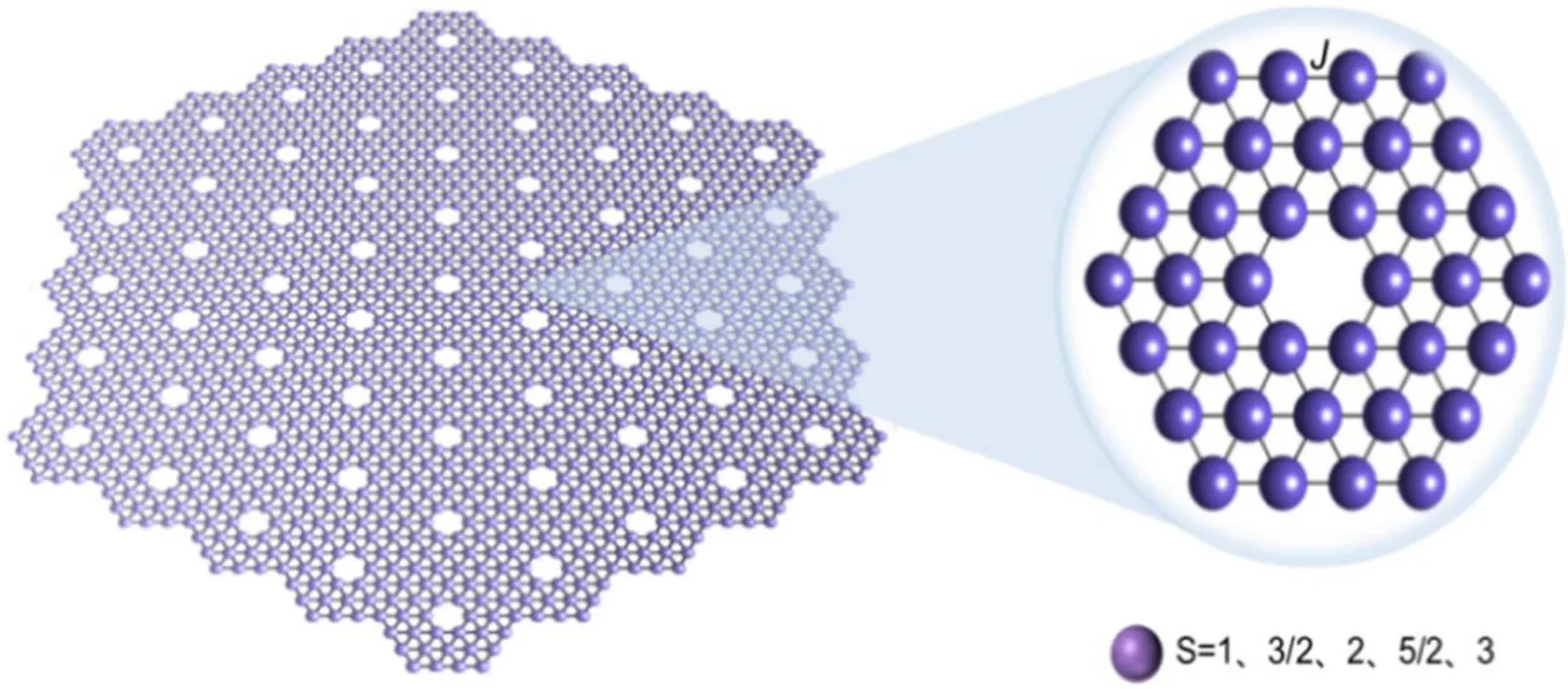
Figure 1.Illustrations of the single-spin (S=1,3/2,2,5/2 and 3) borophene monolayer on the left and the B36 minimum unit enlarged on the right.J is the exchange coupling interaction between the nearest sublattices.

Figure 2.Total magnetization versus MCS for S=2,D=-0.2,h=0.5 and T=1.01.

Figure 3.Effects of different sizes on magnetic susceptibility and critical temperature of the system for fixed parameters S=3/2,D=-0.1 and h=0.

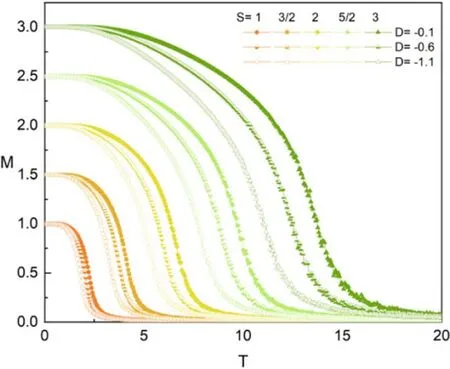
Figure 4.Thermal variation of the magnetization for different spin quantum numbers (S=1,3/2,2,5/2 and 3) and D,and the fixed parameter is h=0.1.

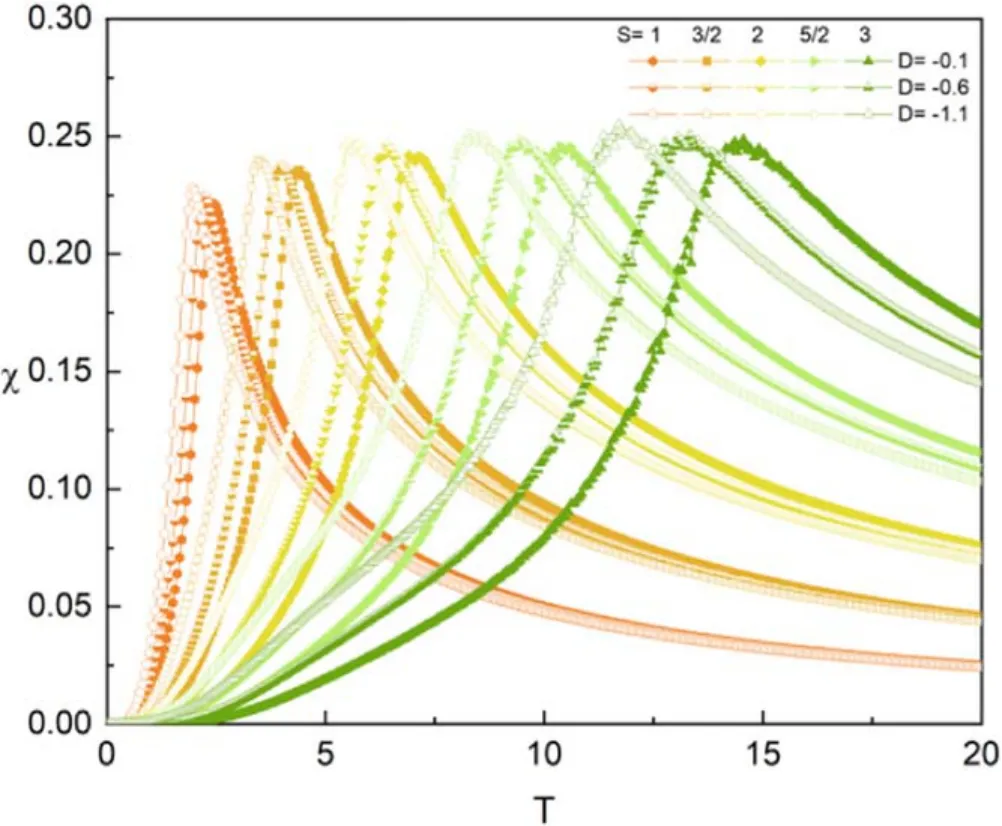
Figure 5.Temperature dependences of χ for various S and D with h=0.1.

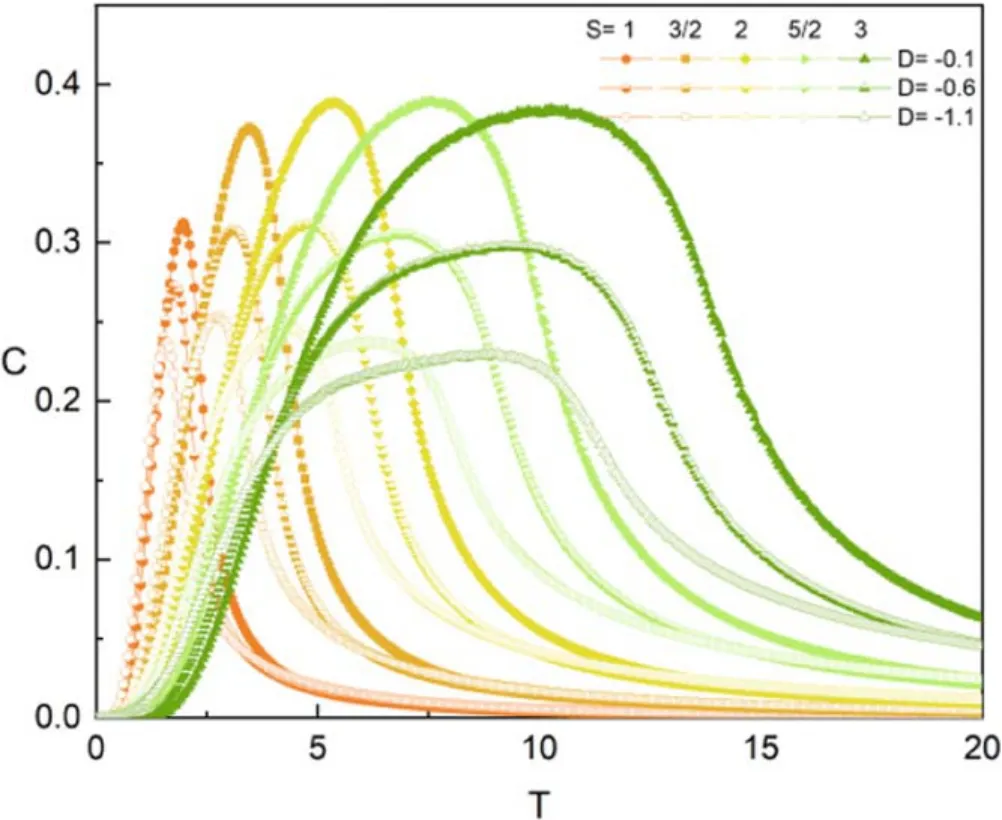
Figure 6.Temperature dependences of C for various S and D with h=0.1.

Figure 7.Temperature dependences of the magnetic entropy for various spin quantum numbers (S=1,3/2,2,5/2 and 3) and D with h=0.1.

Figure 8.Variation of the critical temperature for different spin quantum numbers (S=1,3/2,2,5/2 and 3) and D,and the fixed parameter is h=0.1.

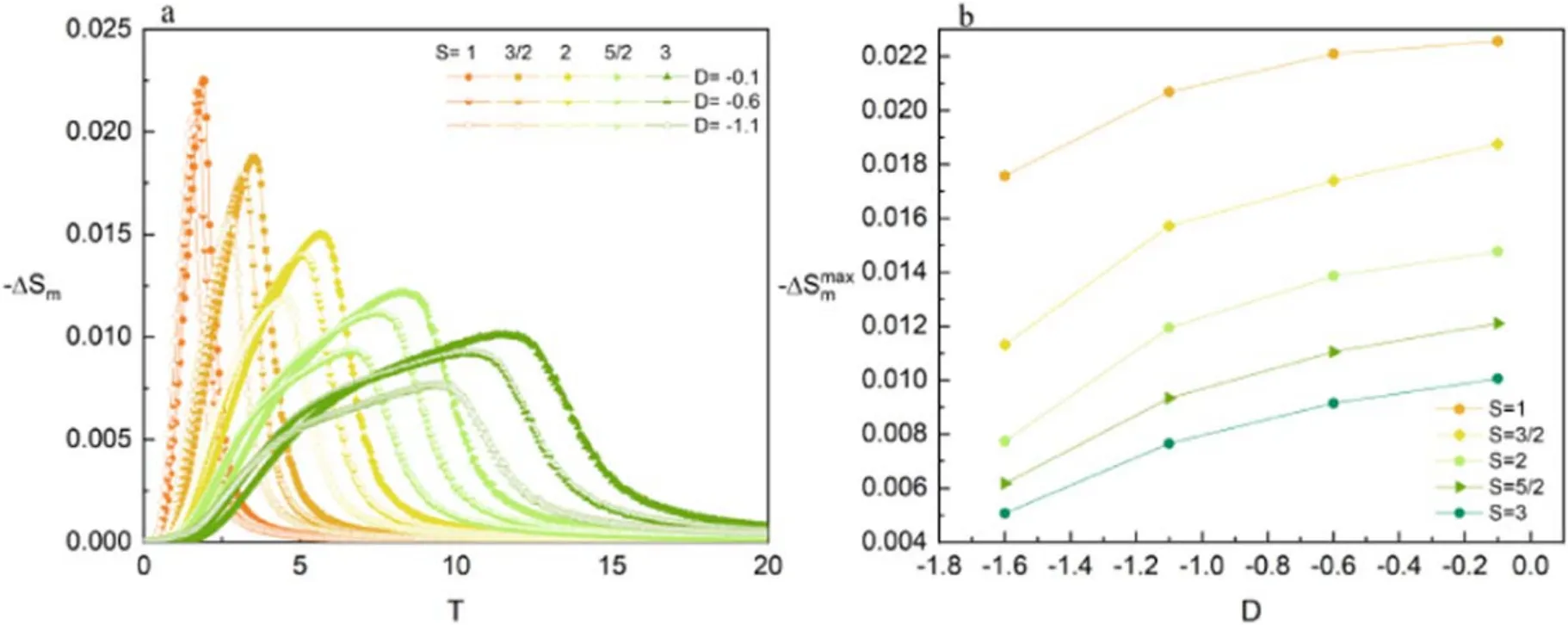
Figure 9.-ΔSm as a function of T for various spin quantum numbers (S=1,3/2,2,5/2 and 3) and D with fixed h=0.1.(b) D dependence of -for various spin quantum numbers (S=1,3/2,2,5/2 and 3) with fxied h=0.1.

Figure 10.-ΔSm as a function of T for various spin quantum numbers (S=1,3/2,2,5/2 and 3) and h with fixed D=-1.1.(b) h dependence of -for various spin quantum numbers (S=1,3/2,2,5/2 and 3) with fxied D.

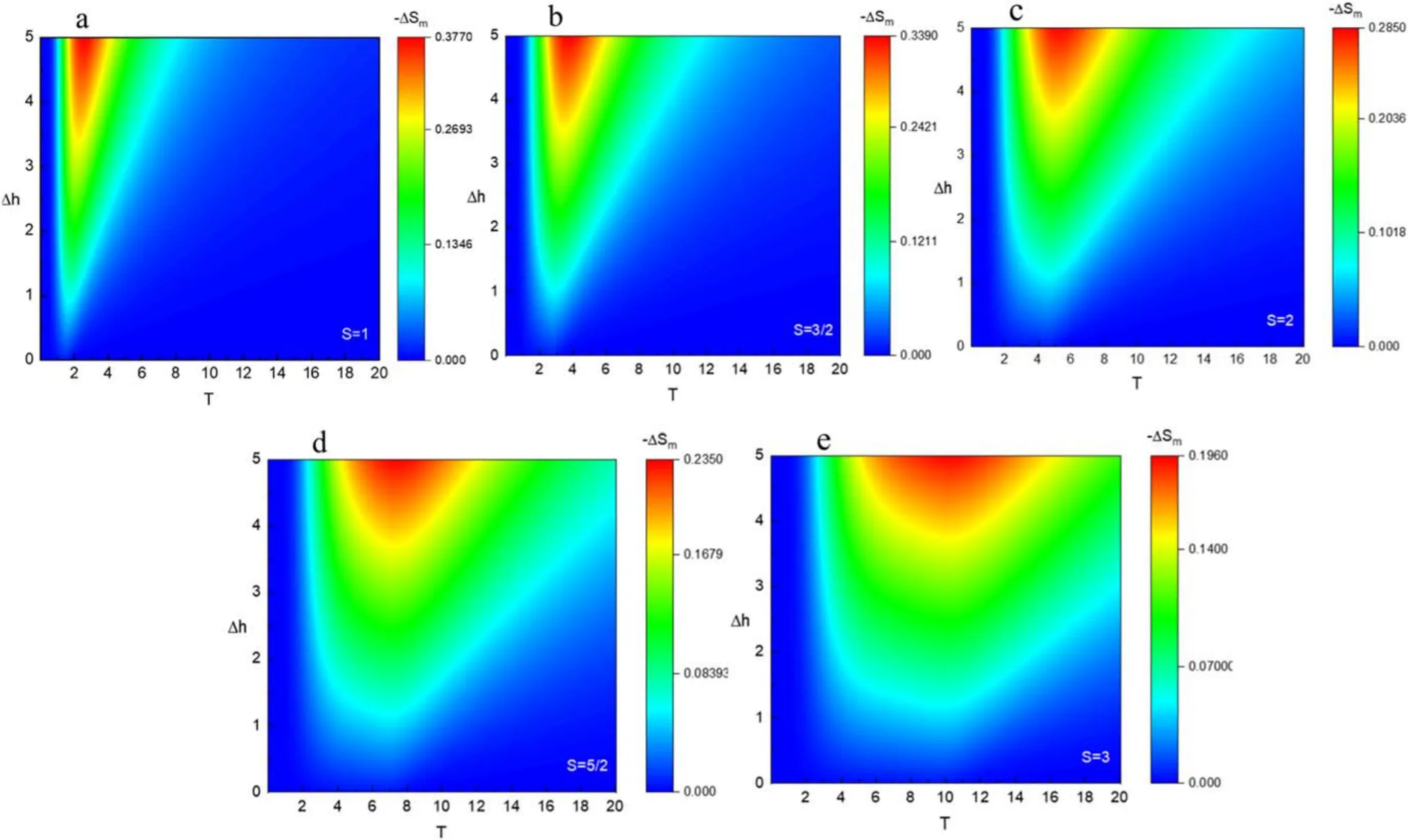
Figure 11.Variation of the -ΔSm under the effects of spin quantum numbers (S=1,3/2,2,5/2 and 3) and T for D=-1.1.

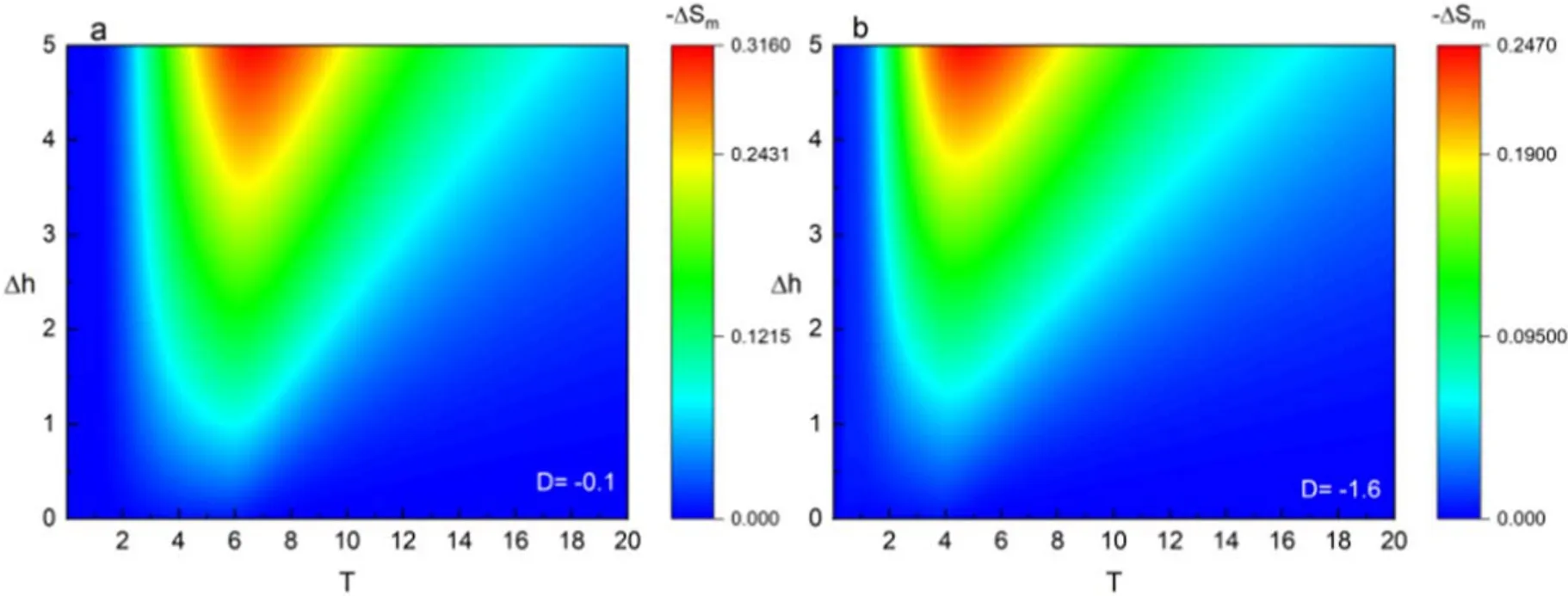
Figure 12.Variation of the -ΔSm under effects of D and T for S=2.

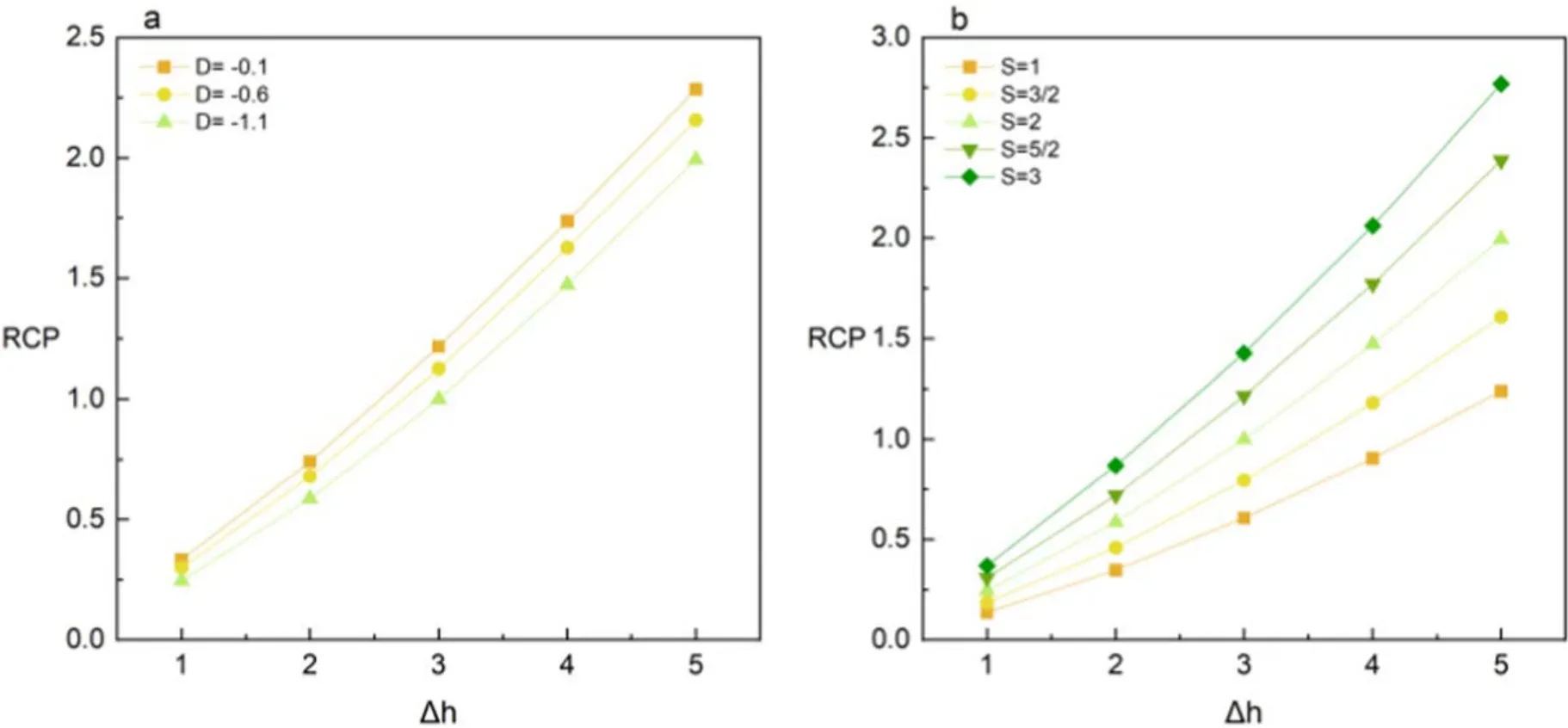
Figure 13.Influence of h on the RCP (a) for various D with S=2;(b) for various spin quantum numbers (S=1,3/2,2,5/2 and 3)with D=-1.1.

The RCP is an important parameter to measure the MCE.In figure 13,we show the dependence of RCP on D and spin quantum numbers.It can be seen from figure 13 that when both D and S are unchanged,the RCP increases with the increase in Δh.This phenomenon has also been reported in the results of a graphdiyne bilayer with Ruderman–Kittel–Kasuya–Yoshida interaction [53].In figure 13(a),when the value of Δh is fixed,such as Δh=5,the RCP decreases from 2.285 to 1.994 with increasing∣D∣ .In contrast,the influence of spin quantum number on RCP is opposite to that of D.The main reason is that the larger the spin quantum number,the more stable the system is,and the corresponding temperature region increases,which is established in figure 11.Consequently,it is concluded that the growth in spin quantum number leads to the increase in RCP,similar to the results in a spin-S (S=1,3/2,5/2,3 and 7/2) Ising model using mean field approximation [46].

3.3.Hysteresis loop

Figure 14 illustrates the change in hysteresis loops of the system for different spin quantum numbers when D=-1.1 and T=1.5.The results show that the borophene monolayer exhibits a single loop regardless of the spin value.Furthermore,the area of the loop expands with the increase in the spin quantum number.More specifically,the coercivity(hc) and the remanence (MR) of the whole system both increase slowly during the process of increasing the spin quantum number.According to the Hamiltonian,it can be seen that with the larger the spin quantum number,the lower the energy and the more stable the system,the hcrequired for demagnetization may increase.

Figure 15 illustrates the influence of diverse values of D on the hysteresis loop of the borophene monolayer for S=2 and T=1.5.Similar to in figure 14,all the curves also exhibit single-loop hysteresis behavior when the spin value is unchanged.The variation trend of the hcand MRis the same as that in figure 14.However,it is found that the influence of spin quantum number on the hysteresis behavior of the system is stronger than that of crystal field D.

Figure 15.Hysteresis loops with different D when S=2 and T=1.5.

Finally,the calculation results of the hysteresis loops as a function of various T are presented in figure 16.It can be clearly seen that the single loop continues to increase with T increasing and disappears at T=5.1,turning into a smooth curve.This indicates that the system becomes the disordered superparamagnetic phase.There have also been some theoretical investigations of borophene nanoribbons with core–shell structure [28],Ising-type polyhedral chain [54] and lowdimensional magnetic nanostructures [55–60],as well as experimental observations of bilayer graphene nanoribbons[61] that have revealed similar temperature dependence on the hysteresis behavior.

4.Conclusion

In summary,the magnetic,thermodynamic characteristics and MCE of a single-spin (S=1,3/2,2,5/2 and 3) Ising borophene monolayer were simulated using the Monte Carlo method.The simulation results show that the spin quantum number and crystal field D have opposite effects on the M,χ,C and S of the borophene monolayer.In addition,we discovered that the stability of the system benefits from an increase in spin quantum number.For MCE,the -ΔSmwould increase as a result of either the increase in Δh or a drop in ∣D∣ and spin quantum number.More importantly,increasing the spin quantum number may promote the increase in RCP.Finally,we anticipate that the obtained results will provide a reasonable guide for further study of MCE in borophene monolayers.