Flocking and clustering in mixtures of selfpropelled particles with or without active reorientation

Lu Chen and Z C Tu

1 Department of Physics,Beijing Normal University,Beijing 100875,China

2 Complex Systems Division,Beijing Computational Science Research Center,Beijing 100193,China

Abstract We study phase behaviors of mixtures comprising active particles with and without active reorientation by varying mixing ratios.We observe that the order parameter characterizing flocking in the steady state exhibits a linear decrease with an increase in mixing ratio.While the order parameter characterizing clustering in the steady state presents a sharp leap as the mixing ratio increases.Particularly,we obtain phase diagrams of flocking under different mixing ratios and observe that the domain corresponding to flocking experiences a contraction with the increase of mixing ratio.Simultaneously,the coordinates of the critical point on the phase boundary between the flocking and the disordered phase decay exponentially with the mixing ratio.

Keywords: active matter,flocking,clustering,binary system

1.Introduction

Active matter,comprising plenty of self-propelled agents that move in fluids or more complex environments [1–3],commonly exists in biological systems and exhibits a variety of exotic collective behaviors,such as traveling wave [4],synchronization [5,6],clustering [7–10],critical coexistence phase [11–13] and so on.Recent advances in the field of active matter have opened up a new realm of research and revealed intriguing phase behaviors in mixtures of active and passive particles [14–20].Dolai et al observed motilityinduced phase separation [14] in binary mixtures of small active and big passive particles with soft repulsive interactions.Wang et al introduced a small number of active particles into a system of passive particles,and then they found that the diffusion of passive particles is enhanced [15].Kolb and Klotsa demonstrated motility-induced phase separation upon varying the activity in binary mixtures of fast and slow self-propelled particles [16].Pearce and Giomi considered an active system consisting of leaders and followers,and investigated how flocks respond to leadership and make decisions [17].Many emergent behaviors of active matter can be well-reproduced by models with an explicit local alignment interaction [21],and an inelastic collision rule [22]between a particle’s orientation and propulsion.However,none of these models explicitly include collision avoidance which is a movement strategy commonly adopted by animals[23–25].In our previous work [26,27],we presented a model of self-propelled disks with active reorientation in analogy to collision avoidance in animal herds.We found the coupling of self-propulsion and active reorientation leads to rich phases including clustering and collective flocking without explicit alignment interaction.

To the best of our knowledge,there is a lack of investigations on binary mixtures of self-propelled particles with or without active reorientation.In this work,we focus on this kind of binary mixture and study the phase behaviors(flocking and clustering) by varying mixing ratios of particles without active reorientation.We find that the order parameter characterizing flocking in the steady state of the system decreases linearly with the increase in mixing ratio.On the contrary,the order parameter characterizing clustering in the steady state sharply rises with the increase of mixing ratio and then reaches a relatively large level.We obtain phase diagrams in the steady state under different mixing ratios.We observe that the domain corresponding to flocking is contracted with the increase of mixing ratio and that the coordinates of the critical point in the phase boundary between the flocking and the disordered phase decay exponentially with respect to the mixing ratio.

Figure 1.Collision avoidance of particles with active reorientation.

The rest of this paper is organized as follows.In section 2,we briefly introduce our model and simulation method.In section 3,we discuss the evolution of order parameters under different mixing ratios.In section 4,we explore phase diagrams in the steady state under different mixing ratios.The last section is a brief summary.

2.Model and method

Our study focuses on an active collision avoidance model,which was developed in our previous work [27].This model comprehensively incorporates collision avoidance within interaction rules,which is a common strategy observed in motile animals moving in herds.As shown in figure 1,when two particles imminently collide,they can actively adjust their orientations to avoid collisions.That is,active reorientation only occurs at the moment of collisions.The model consists of self-propelled disks with a diameter d in a two-dimensional square box of length L.The total number of disks is N,and the position of disk i is denoted as ri.The self-propulsion direction of disk i is denoted byni≡(c osθi,sinθi),where θirepresents the angle between the self-propulsion direction of disk i and the x-axis.The motion of the disk i is governed by the following equations:

The first equation describes the translational motion of disk i.Here,v0denotes the magnitude of self-propelled velocity and μ is the mobility.Fijis the force acting on disk i from disk j,which is expressed as Fij=k(d -rij)ε(rij-d)rij/rij,where rij≡ri-rjand rij≡|ri-rj|.ˆzis a normal vector of the plane pointing to the reader.ε(·) represents the Heaviside function.Parameter k represents the strength of the two-body interaction between disks.The first term in the right-hand side of equation (1) indicates that when the disk i does not overlap with other disks,it is self-propelled.The second equation describes the rotational motion of disk i.ηi(t) is Gaussian white noise with 〈ηi(t)〉=0 and 〈ηi(t)ηj(t′)〉 =σ2δi jδ(t-t′),where σ represents the strength of noise.αiδ(t) is the angular velocity,generated by active reorientation when two disks get close to each other.This term indicates that active reorientation only occurs at the moment of collisions.Here we consider a mixture with two types of self-propelled particles.One comprises normal particles with active reorientation,while the other consists of abnormal particles without active reorientation.If disk i is a normal particle,αiis assigned to a positive value α.If disk i is an abnormal particle,αiis zero,which means disk i can not actively reorient when it gets close to other disks.

We investigate phase behaviors in this binary mixture.The proportion of abnormal particles in the mixture is named mixing ratio q.We randomly select abnormal particles for a given q in initial states and observe corresponding steady states.We find two distinctive phases in the steady state under different mixing ratios.One is flocking,where almost all particles move roughly in the same direction.The other is clustering,where a certain amount of particles aggregate together.In figure 2,we present snapshots of initial states and steady states under q=0.01 and q=0.1.

When a small number of abnormal particles are initially introduced into the system (q is 0.01) withα=0.01,=0.01,starting from a random state [fgiure 2(a)],the system eventually evolves to a flocking state as shown in figure 2(b).Figure 2(c) presents the initial random state with q=0.1.The system finally evolves into a clustering state[(figure 2(d)] rather than a flocking state.For more detailed observations,we find that normal and abnormal particles are still mixed together without separation.And that their distribution appears relatively uniform.

Figure 2.Snapshots of initial states and steady states of the system under different mixing ratios.Red represents normal particles.Blue represents abnormal particles.Black arrows indicate the direction of particle velocity.(a) initial state (disordered phase) with q=0.01.(b)steady state (flocking) with q=0.01.(c) initial state (disordered phase) with q=0.1.(d) steady state (clustering) with q=0.1.

3.Evolution of order parameters under different mixing ratios

In the previous section,we observed that different mixing ratios result in two different phases (flocking and clustering)in the steady state.In this section,we consider the evolution of two order parameters characterizing the flocking and clustering phases from a quantitative point of view.

The flocking phase is described by an order parameter defnied byM=,where the average 〈〉is taken over all N particles.M ≈0 indicates a disordered phase,whereas M ≈1 indicates perfect flocking.Clustering is characterized by another parameter ρ which is specified as below.We measure the local density for each disk by calculating the Voronoi cell [28].By numerical simulation,we find that when local density is larger than a certain threshold[26],the disk is located in a certain dense cluster.Then ρ is defined by the fraction of particles located in the dense cluster[29].ρ ≈0 indicates no cluster phase,whereas ρ ≈1 perfect cluster phase.

The evolutions of order parameters M and ρ with α=0.01,=0.01 are shown in figure 3,from which we find that the introduction of abnormal particles hinders flocking while enhancing the formation of clusters.The time evolution of M under different mixing ratios is shown in figure 3(a).When the system starts from a homogeneous state with an initial random distribution of orientation and position,as we can see,for q ＜1,M exhibits a clear growth with time,then tends to saturation value around 2,000,000 timesteps,and then eventually reaches a steady value.With q increasing,the degree of flocking decreases when the system reaches a steady state.The flocking is suppressed since the abnormal particles disrupt the alignment between the normal particles with active reorientation.Figure 3(b) shows the time evolution of ρ under different mixing ratios.When q is small,ρ develops a peak at the first stage and then goes through a sharp descent.This indicates that clusters are formed and then disintegrated.When q is large enough,ρ still remains a finite value finally.This implies that the clusters robustly exist rather than disappear.

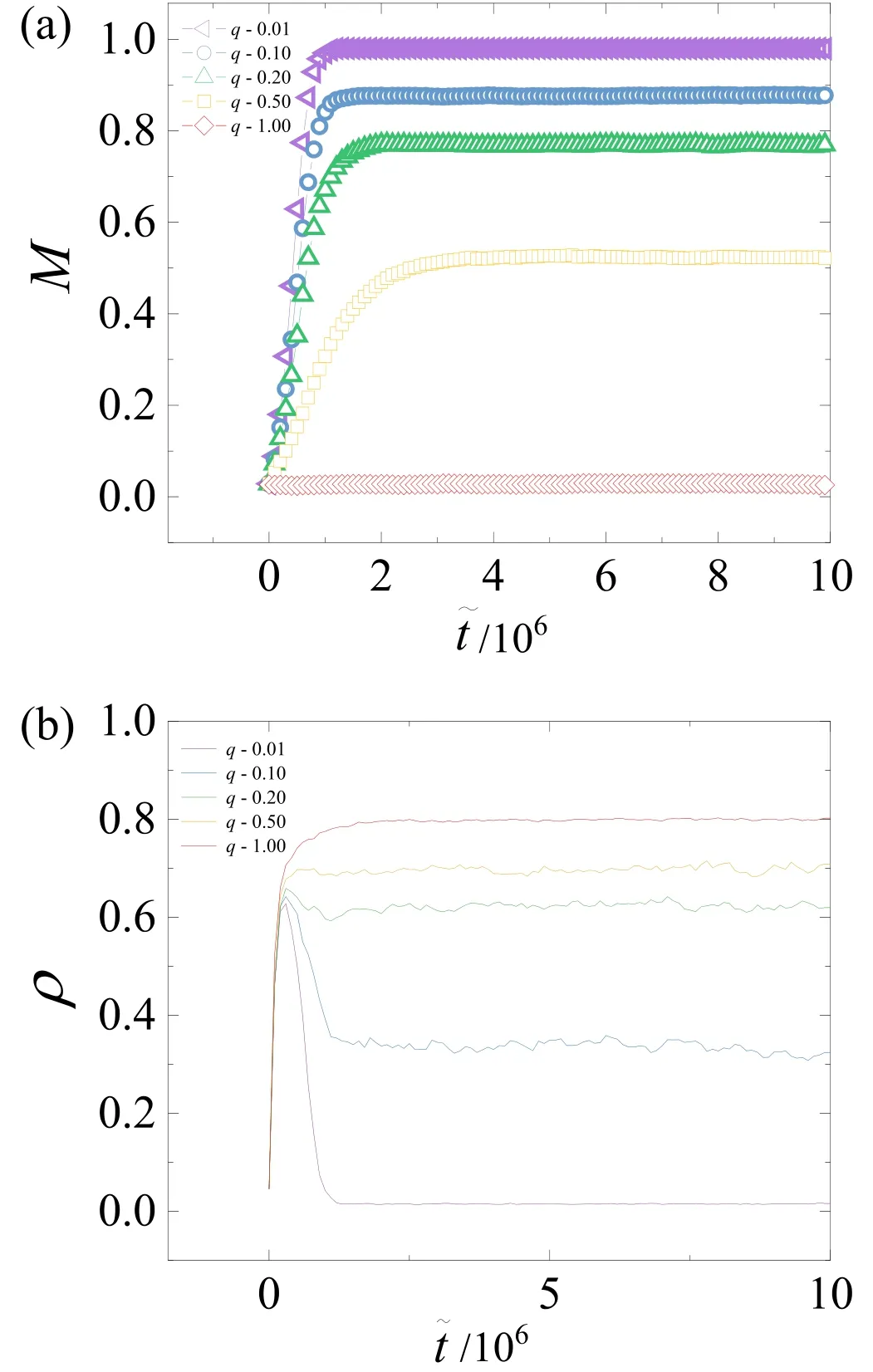
Figure 3.Time series of order parameters under different mixing ratios: (a) The evolution of M;(b) The evolution of ρ.

Figure 4.Order parameters in steady states under different mixing ratios.Hollow points: Ms as a function of q;solid points: ρs as a function of q.

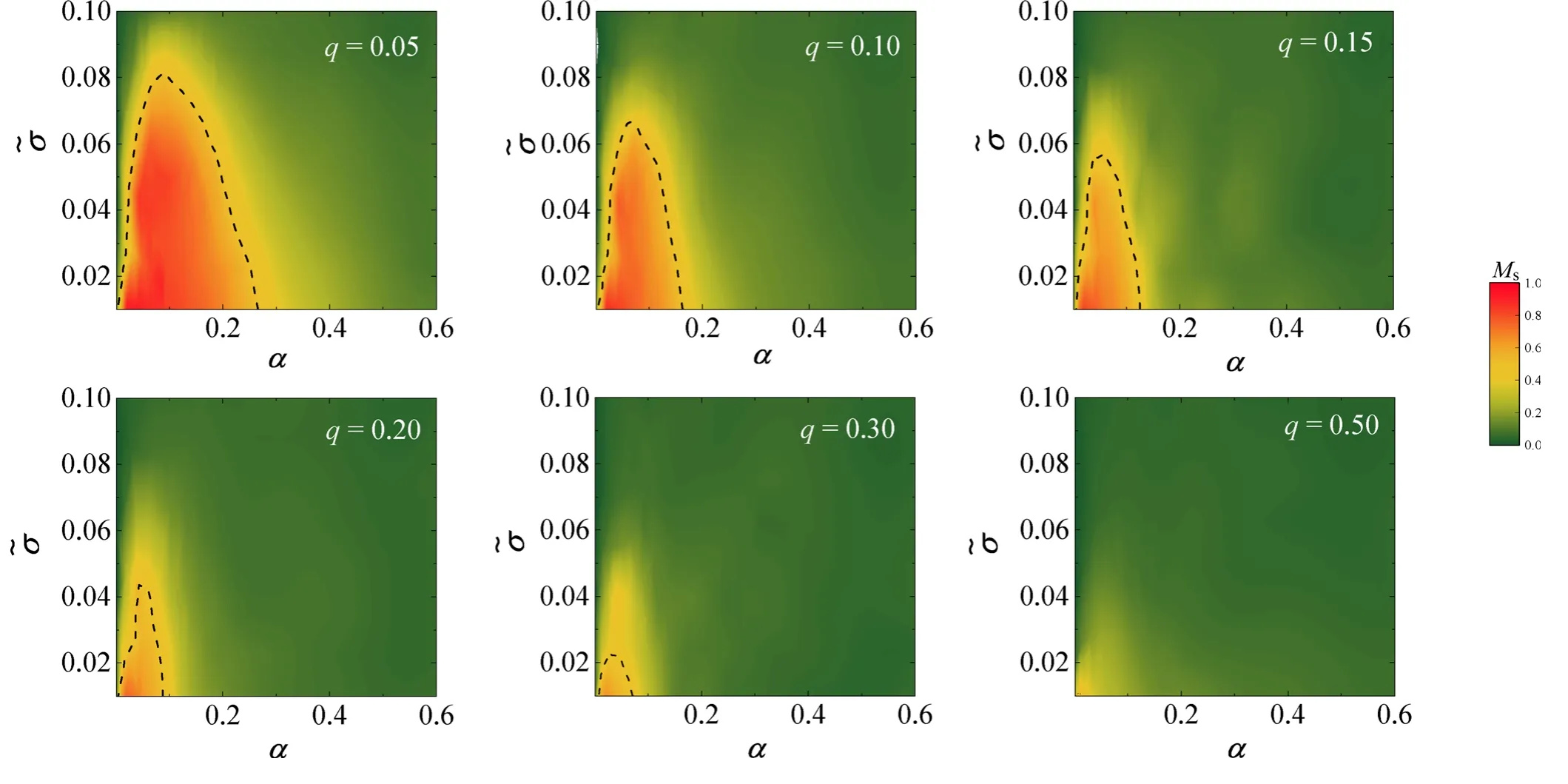
Figure 5.Phase diagrams with different mixing ratios.Mixing ratio q=0.05,0.10,0.15,0.20,0.30 and 0.5,respectively.

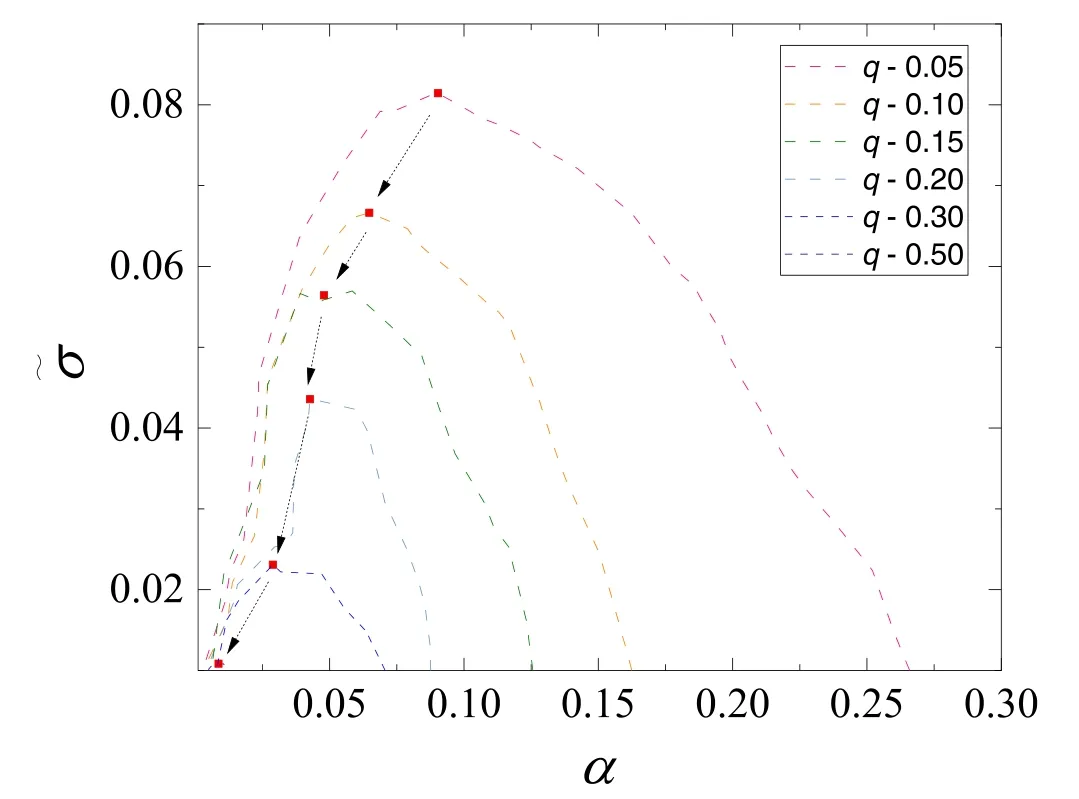
Figure 6.Contour lines with Ms=0.5 and critical points under q=0.05,0.10,0.15,0.20,0.30 and 0.5 in {α,˜σ} space.

Figure 7.The relationship between αc,and q.We show the error bar for αc since the values of αc cannot be accurately extracted from the phase diagram.

Comparing figure 3(a) and figure 3(b),we observe that the timescale for the formation of flocking states exceeds that for the system reaching a metastable clustering state.The underlying cause for the above phenomenon is that clustering is a relatively rapid process that involves local particle rearrangements,while flocking is comparatively slow due to the negotiation of particle orientations throughout the entire system.

In figure 3,we specifically present two extreme cases.When q=1 the system exhibits a disordered state (M ≈0)and highly clustering phase (ρ ≈0.8) in the steady state,which is consistent with the results in previous work [7].When q approaches 0,the steady state of the system is highly ordered (M ≈1) without clustering (ρ ≈0) which is consistent with previous work [27].

4.Steady states under different mixing ratios

In this section,we focus on steady states of the system.Order parameters in the steady state withα=0.01,=0.01under different mixing ratios (q=0.05,0.1,0.2,0.5,1.0) are presented in figure 4,where Msand ρsrepresent the values of M and ρ in the steady state,respectively.Hollow points in figure 4 imply a pretty good linear relationship between Msand q,which may be expressed as:

Here, M0should depend on both α and ˜σ.In figure 4,the fitted value of M0is 0.98.This linearity is qualitatively understood as follows: the presence of abnormal particles disrupts the alignment between the normal particles with active reorientation,leading to the suppression of flocking.Solid points in figure 4 show ρsversus different mixing ratios,which suggests a behavior of Heaviside-like function.A transition occurs at q=0.1,which indicates that 10% of abnormal particles will lead to a qualitative change in the system.

Next,we investigate the phase diagram of flocking in the steady state with different mixing ratios.For given q,we calculate Mswith different sets of α and ˜σ.The results are shown in figure 5.The phase boundaries between flocking and disordered phases are determined by the contour line corresponding to Ms=0.5 (dash lines shown in figure 5).According to previous studies [8],the steady state of active systems merely with self-propulsion is clustered and disordered.That means when α=0,no matter what the value of ˜σis,M should be around 0,which implies that flocking can not appear in the steady state.However,introducing active reorientation allows the system to ultimately evolve to an ordered state (flocking) in the steady state [27].When two particles get close to each other,small active reorientation(α is small) promotes local velocity alignment,while large active reorientation (α is large) makes the orientations of particles adjust too much to align properly.Thus,small α facilitates the formation of flocking,but large α makes the system tend to be disordered.And as we know,it is obvious that large random noise will disrupt flocking and make the system disordered.Therefore,the phase diagram in figure 5 is the result of competition between α (related to scattering) and ˜σ(related to self-diffusion).The necessary conditions for the formation of flocking are as follows: (i) α is nonvanishing but not too large;(ii) the noise is relatively small such that α plays a dominant role.Under the constraints of the above conditions,the region of flocking in the phase diagram presents an arched shape as shown in figure 5.When noise is absent,both too small and too large α can not make orientations of two particles align perfectly,so an optimal α exists in the system.Under this optimal α,the system reaches the most ordered state.As the strength of noise increases,the degree of order of the system will gradually decrease.When the strength of noise exceeds a certain threshold,the order is disrupted.This threshold and the optimal α determine the coordinates of the critical point in the phase diagram.

From figure 5,we find that the domains of flocking shrink with the increase of q.We extract phase boundaries corresponding to different q from phase diagrams and specially mark the coordinates (αc,) of each critical point according to each phase boundary as shown in figure 6.We observe that bothand αcdecrease and move towards the origin with the increase of q.The shrink of the domains of flocking and the movement of the critical point can be intuitively understood as follows: the presence of abnormal particles disrupts the alignment between the normal particles with active reorientation,which is equivalent to reducing the contribution of α.Therefore,the more abnormal particles are introduced,the harder the formation of flocking.In figure 7,we specially demonstrate the relationship between αc,and q.By fitting the data,we find that both αcanddecay exponentially with respect to q,that is,αc=0.11e-5.2qand=0.10e-4.5q.

5.Conclusion and discussion

In this paper,we demonstrate the effect of mixing ratio on flocking and clustering.Unlike previous work which focuses on mixtures of passive particles and self-propelled particles[14,15,18],our study concentrates on a mixture of selfpropelled particles with or without active reorientation when two particles get close to each other.Our work reveals a clearly linear decrease in the degree of flocking in the steady state of the system as the mixing ratio increases.We have constructed phase diagrams for the steady state under various mixing ratios.Notably,the coordinate of the critical point on the phase boundary between flocking and disordered phases shows an exponential decay with respect to the mixing ratio.However,we cannot provide a theoretical explanation for these quantitative relations mentioned above at the present stage.We look forward to theoretical explanations and experimental investigations on these compelling findings in the future.

Acknowledgments

We wish to acknowledge helpful suggestions from X L Xu.We also thank computational support from the Beijing Computational Science Research Center.The research was supported by the National Natural Science Foundation of China (Grant No.11 975 050).