金相显微镜畸变的测量不确定度评定

余泽利, 房永强, 杨军红,2, 张 兵,张艺新, 郑 铱, 毕革平

(1.西安汉唐分析检测有限公司，陕西 西安 710201；2.西北有色金属研究院，陕西 西安 710016)

1 引 言

测量结果的不确定度[1,2]是表征合理地赋予被测量之值的分散性、与测量结果相联系的参数。在科学技术生产活动中,测量不确定度的大小严重影响测量水平的高低,测量不确定度越小,测量结果越接近真实值,测量结果越准确可靠,其使用价值越高。反之,测量不确定度越大,测量结果远离被测量真实值,使用价值也越低。因此,测量结果的表示必须有测量不确定度的说明[3,4]。

金相显微镜畸变[5～8]是显微镜的横向放大率随视场的增大而变化所引起的一种与失去物像相似的像差。金相显微镜由物镜、中间透镜和目镜组成。由于畸变的存在,导致金相显微镜目镜中观察到的实际像与理想像存在偏差,影响测量结果的准确性。因此,通过金相显微镜畸变的测量不确定度评定,可以判断金相显微镜图像变形失真情况。

本文根据《一种光学显微镜系统畸变测量方法》[9]和《测量不确定度评定与表示》校准规范[10],对金相显微镜畸变测量过程进行研究,分析各因素引入的不确定度大小及权重,为金相显微镜畸变测量结果的准确性提供参考。

2 材料与方法

2.1 材料与仪器

A型“米字形”线纹尺[11],测量范围0～100 mm,分度值1 mm,其它级别,如图1所示;B型“米字形”线纹尺,测量范围0～1.6 mm,分度值0.01 mm,二等尺,如图2所示;数字照相机,富士E900,4 608 pixel×3 456 pixel,图片传输用该相机配套的数据线及软件;金相显微镜,Zeiss AX10,总放大倍率50×、100×、200×、500×和1 000×。

图1 A型“米字形”线纹尺Fig.1 Type A “meter shaped” linear ruler

图2 B型“米字形”线纹尺Fig.2 Type B “meter shaped” linear ruler

2.2 实验方法

2.2.1 测量原理

金相显微镜畸变采用B型“米字形”线纹尺和畸变测量系统进行测量。其中畸变测量系统包括紧贴在显微镜目镜上的数码相机、连接显微镜目镜与数码相机摄像头的相机固定装置[12]、图片传输及测量软件,结构图见图3。

图3 金相显微镜畸变测量系统结构图Fig.3 The structural diagram of metallographic microscope distortion measurement system

通过设置B型“米字形”线纹尺对显微镜系统畸变进行测量,数码相机拍摄显微镜目镜下的“米字形”线纹尺的图像,再通过测量图像上4个方向不同长度所占的像素数来计算显微镜系统畸变;由于米字形线纹尺有4个不同方向的直线线纹尺,因此1次拍摄的图像即可作为全部测量的对象,减少了由于数码相机拍摄的问题导致的测量误差,使测量结果更加准确。

畸变测量系统的畸变采用A型“米字形”线纹尺、3级平板[13]、5等量块[14](250 mm)进行测量,通过量块控制数码相机距A型“米字形”线纹尺250 mm,且相机中心和线纹尺中心重合,用数码相机采集相距250 mm且垂直、对中的A型尺图像,见图4,通过测量图像上4个方向不同长度所占的像素数来计算畸变测量系统的相对畸变。A型、B型“米字形”线纹尺依据JJG 73—2005《高等别线纹尺检定规程》[15]进行校准。

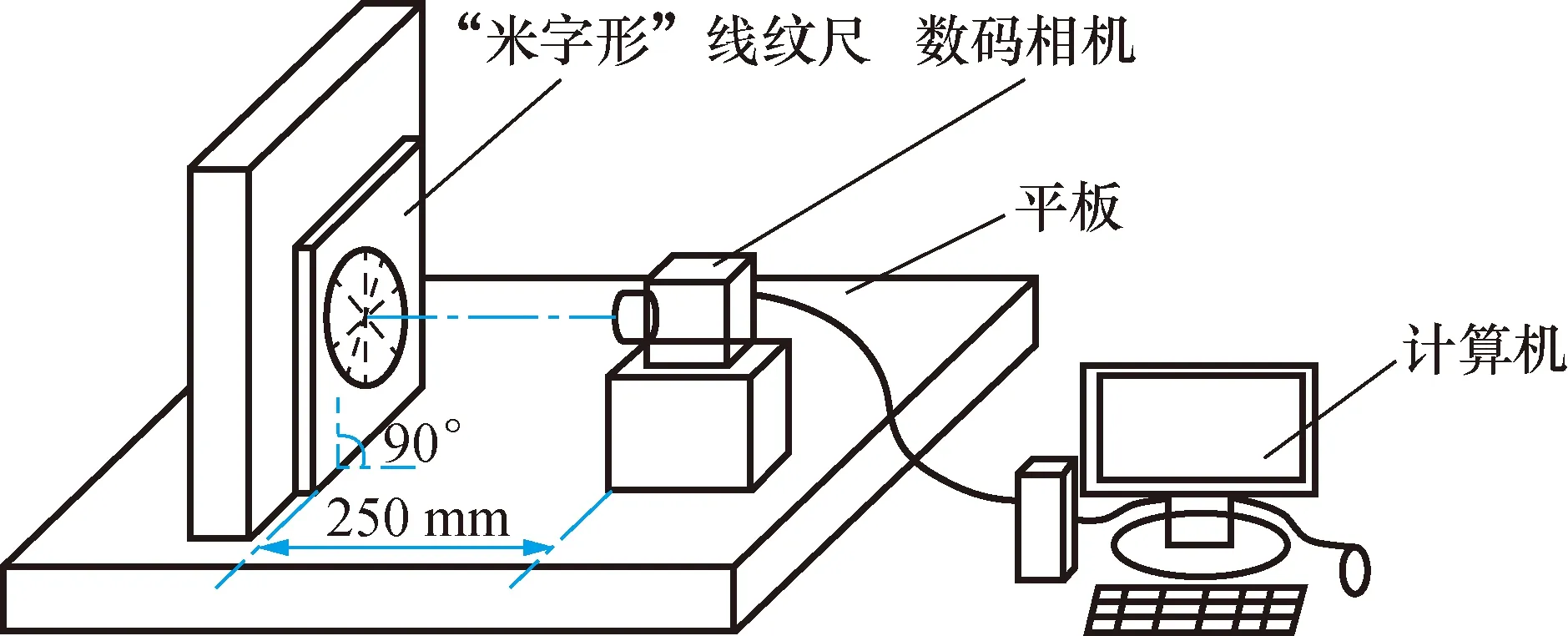
图4 数码相机采集A型“米字形”线纹尺结构图Fig.4 The structure diagram of type A “meter shaped” linear ruler collected by digital camera

2.2.2 测量方法

采用数字照相系统采集显微镜目镜中的数字图像,测量数字图像指定4个方向(0°、45°、90°、135°)的中心对称间距d和D,原理图见图5。测量的d值作为理论基准,k×d作为D的理论值,D的实际值与理论值的相对偏差(相对畸变)作为显微镜畸变的定量指标。

图5 数字图像原理图Fig.5 The schematic diagram of digital image

2.2.3 测量步骤

将B型“米字形”线纹尺放置金相显微镜的载物台上,在目镜上安装数字照相机,确保相机与目镜0距离且中心重合[16,17],设置金相显微镜物镜放大倍数分别为5×、10×、20×、50×和100×,调整线纹尺位置,使线纹尺中心与目镜十字中心重合,通过测量软件采集不同总放大倍率下目镜中线纹尺的图像,见图6。

图6 畸变测量系统中B型线纹尺视场图Fig.6 The field of view of type B ruler in distortion measurement system

2.2.4 数学模型

金相显微镜畸变数学模型为:

(1)

式中:k为金相显微镜视场系数,k=4～10;D和d为金相显微镜目镜中B型“米字形”线纹尺数字图像中心对称间距,pixel。

金相显微镜畸变测量系统畸变数学模型为:

(2)

式中:k′为视场系数,k′=10;D′和d′为测量系统中A型“米字形”线纹尺数字图像中心对称间距,pixel。

3 结果与分析

3.1 分析不确定度的来源

测量不确定度的评定分为A类评定和B类评定。A类评定:在重复性、复现性、期间精密度测量条件下,测量结果用贝塞尔公式法和极差法进行不确定度评定,一般测量次数n小于10次时,可采用极差法,本文选择贝塞尔公式法。B类评定:根据有关信息估计的先验概率分布得到的不确定度。

通过对影响测量结果的各因素进行研究,结合畸变和畸变测量系统数学模型,分析不确定度来源,主要包括:测量重复性、显微镜畸变测量系统畸变、B型“米字形”线纹尺、环境温度、线膨胀系数等,见图7。其中环境温度和线膨胀系数对测量结果不确定度影响较小,可以忽略不计。输入量D和d测量重复性属于A类评定,分辨力、线纹尺示值误差等属于B类评定。

图7 不确定度来源因果图Fig.7 The cause and effect diagram of uncertainty sources

本文以总放大倍率为500×为例,对金相显微镜畸变测量结果进行不确定度评定。

3.2 输入量D引入的不确定度u(D)

3.2.1 重复测量D引入的u1(D)

重复测量D引入的u1(D)属于A类不确定度。在重复性条件下,金相显微镜总放大倍率选择500×,对B型“米字形”线纹尺0°、45°、90°、135°四个方向D重复测量10次,计算4个方向10次测量结果的算术平均值,根据贝塞尔公式,求得4个方向的标准偏差sj分别为2.0,1.4,3.4,2.1 pixel。重复测量中心对称间距D=0.16 mm(k=8),引入的不确定度详见表1。根据合并样本标准偏差sp公式,求得

表1 重复测量D引入的不确定度Tab.1 Uncertainty introduced by repeated measurement D pixel

实际测量4次,以算术平均值作为测量结果,则求得重复测量D引入的u1(D)为:

3.2.2 显微镜畸变测量系统畸变引入的u2(D)

显微镜畸变测量系统畸变引入的u2(D)可以分为两大类,一类是输入量D′引入的u(D′),包括重复测量D′引入的u1(D′)、测量系统分辨力引入的u2(D′)、A型“米字形”线纹尺畸变引入的u3(D′);另一类是输入量d′引入的u(d′),包括重复测量d′引入的u1(d′)、测量系统分辨力引入的u2(d′)、A型“米字形”线纹尺畸变引入的u3(d′)。

1) 输入量D′引入的u(D′)

重复测量D′引入的u(D′)属于A类不确定度。在重复性条件下,数码相机采集相距为250 mm,对A型“米字形”线纹尺0°、45°、90°、135°四个方向D′重复测量10次,计算4个方向10次测量结果的算术平均值;根据贝塞尔公式,求得4个方向的标准偏差分别为1.9,1.0,2.0,1.8 pixel。重复测量中心对称间距D′=100 mm(k=10),引入的不确定度详见表2。根据合并样本标准偏差公式,求得

表2 重复测量D′引入的不确定度Tab.2 Uncertainty introduced by repeated measurement D′ pixel

实际测量4次,以算术平均值作为测量结果,则求得重复测量D′引入的u1(D′)为:

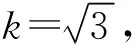
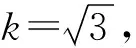
由于重复性引入的u1(D′)大于分辨力引入的u2(D′),可以不考虑分辨力引入的不确定度分量。其它输入量之间彼此独立不相关,则输入量D′引入的u(D′)为:

2) 输入量d′引入的u(d′)

d′重复测量引入的u(d′)属于A类不确定度。在重复性条件下,数码相机采集相距为250 mm,对A型“米字形”线纹尺0°方向d′=10 mm重复测量10次,测试结果分别为158,156,156,154,154,156,158,154,154,156 pixel,测得平均值为155.6 pixel,根据贝塞尔公式,求得标准偏差为:

实际测量10次,以算术平均值作为测量结果,则重复测量d′引入的u1(d′)为:

输入量d′与输入量D′采用同一套测量系统,分辨力相同,则u2(d′)=u2(D′)=0.29 pixel。

根据第3.2.2节中1)可知,A型“米字形”线纹尺畸变引入的u3(d′)=u3(D′)=0.0018 pixel。

由于重复性引入的u1(d′)大于分辨力引入的u2(d′),可以不考虑分辨力引入的不确定度分量。其它输入量之间彼此独立不相关,则输入量d′引入的u(d′)为:

3) 显微镜畸变测量系统畸变引入的u(q′)的合成

根据式(2),可以得出灵敏系数分别为:

输入量D′和输入量d′是采用同一套测量系统和同一个线纹尺,故为正强相关,其相关系数r(D′,d′)=1,根据不确定度传播规律可知,显微镜畸变测量系统相对畸变引入的uc(q′)为:

=0.27%

当d=128.4 pixel、k=8时,测量系统畸变引入的u2(D)为:

u2(D)=k·d·uc(q′)=2.77 pixel

3.2.3 B型“米字形”线纹尺畸变引入的u3(D)

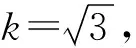
3.2.4 输入量D引入的u(D)的合成

由于测量重复性、测量系统畸变、B型“米字形”线纹尺畸变之间彼此独立不相关,根据不确定度传播规律可知,输入量D引入的u(D)为:

3.3 输入量d引入的u(d)

3.3.1 重复测量d引入的u1(d)

重复测量d引入的u1(d)属于A类不确定度。在重复性条件下,金相显微镜总放大倍率选择500×,对A型“米字形”线纹尺0°方向d=0.02 mm重复测量10次,测试结果分别为128,127,128,129,130,128,127,128,129,130 pixel,测得平均值为128.4 pixel,根据贝塞尔公式,求得标准偏差为:

实际测量10次,以算术平均值作为测量结果,则重复测量d′引入的u1(d′)为:

3.3.2 测量系统畸变引入的u2(d)

输入量d与输入量D采用同一套测量系统,根据第3.2.2节可知,金相显微镜畸变测量系统相对畸变引入的uc(q′)=0.27%,当d=128.4 pixel时,测量系统畸变引入的u2(d)为:

u2(d)=d·uc(q′)=0.35 pixel

3.3.3 B型“米字形”线纹尺畸变引入的u3(d)

根据第3.2.3节可知,当测量系统中心对称间距d=128.4 pixel、k=8时,B型“米字形”线纹尺畸变引入的u3(d)=u3(D)=0.39 pixel。

3.3.4 输入量d引入的u(d)的合成

由于测量重复性、测量系统畸变、B型“米字形”线纹尺畸变之间彼此独立不相关,根据不确定度传播规律可知,输入量d引入的u(d)为:

3.4 合成不确定度

根据式(1),可以得出灵敏系数分别为:

输入量D和输入量d是采用同一套测量系统和同一个线纹尺,故为正强相关,其相关系数r(D,d)=1,根据不确定度传播规律可知,金相显微镜畸变测量结果的合成不确定度uC(q)为:

=0.19%

3.5 扩展不确定度

在置信概率P=95.45%条件下,取k=2,则在总放大倍率为500×时,金相显微镜相对畸变测量结果的扩展不确定度为:

U(q)=k×uC(q)=2×0.19%≈0.4%

根据式(1)计算金相显微镜相对畸变:

当总放大倍率为500×时,金相显微镜相对畸变测量结果表示为(0.4±0.4)%,k=2。

采用相同的方法,对金相显微镜其他总放大倍数下金相显微镜相对畸变进行测量,测量结果和扩展不确定度汇总如表3所示。

4 结 论

测量不确定度评定可为测量结果准确性和可靠性提供理论依据,试验发现,畸变测量系统和重复性测试是显微镜畸变测量结果不确定度的主要因素。利用“米字形”线纹尺和畸变测量系统测量金相显微镜不同放大倍率下相对畸变,取包含因子k=2,置信水平为95%时,在总放大倍率为50×、100×、200×、500×和1 000×条件下,金相显微镜的相对畸变测量结果分别为(0.5±0.4)%、(0.3±0.6)%、(1.3±0.4)%、(0.4±0.4)%、(0.9±0.1)%,满足金相显微镜相对畸变最大允许误差的校准需求。