Integrity analysis and inverse Deng’s grey relational analysis model

Wang Wenping Ma Zheng

(1School of Economics and Management,Southeast University,Nanjing 211189,China)(2National School of Development and Policy,Southeast University,Nanjing 211189,China)(3Institute of Strategic Development,China Telecom Research Institute,Shanghai 200122,China)

Abstract：An inverse Deng’s grey relational analysis model is established to identify and quantify the inverse relationships in the system from a holistic perspective.The axiom system containing inverse relationships is constructed based on the four axioms of grey relational analysis.The inverse Deng’s grey relational analysis model is established by introducing the incidence direction vector,and the incidence direction of factors is identified using an agenetic algorithm.The rationality and effectiveness of the proposed model are verified by identifying the key relevant factors of the innovation chain quality in Jiangsu.The case analysis shows that the inverse grey relational analysis model identifies the knowledge innovation link of the process characteristic as the inverse relational factor of Jiangsu innovation chain quality,with a relational degree of-0.815.Compared with the other four typical grey relational analysis models,its incidence direction and strength judgment are more reasonable.The proposed model can effectively identify and quantify inverse relationships while ensuring analysis integrity,which broadens the application scope of Deng’s grey relational analysis model.

Key words：inverse Deng’s grey relational analysis; grey relational axiom; grey relational degree; genetic algorithm

Grey relational analysis (GRA) is a method used to quantify and sequence the factors affecting the behavior of a system.GRA is useful for systems lacking data or information.Typically,there is a universal promotional or restrictive relationship between the factors influencing a system and its behavior.The interactions between these promotional and restrictive factors provide the necessary impetus for the evolution and development of system self-organization.However,existing research on GRA theories and applications has mainly focused on system factor promotion and ignored restrictive or inhibitory factors.This limitation has hindered a more comprehensive understanding of system development and evolution.To address this gap,the inverse GRA is gaining attention as a new research direction in the field of GRA theory[1].This approach intends to clarify the development and optimization mechanisms of the system.By considering the role of restrictive or inhibitory factors,the inverse GRA provides a more holistic perspective on system behaviors.As a result,the analysis can enrich the scope and depth of research on system development and evolution.

Deng[2],the founder of the grey system theory,proposed that the essence of GRA is comparison,which involves a reference system and a measure.The metric space and point set topological space are combined to create an overall comparison with a reference frame and measure.Deng’s GRA model investigates the major and minor factors of system formation and change by comparing the closeness of various data sequence curves.Numerous improved models based on Deng’s GRA model have been proposed.For instance,Liu et al.[3]introduced an absolute GRA model to measure the area between data sequence curves.By examining the similarity of geometric shapes and spatial distance between data sequence curves,Liu et al.[4]presented the similarity and closeness degrees of the grey relational model,respectively.However,Deng’s GRA model calculates the grey relational degree based on relational coefficients of specific points,which,some argue,leads to information loss.To address this point,the concept of grey entropy was introduced,and the grey relational entropy model was proposed[5].Quan et al.[6]employed the maximum entropy method to calculate the weight of relevant factors and proposed a weighted GRA model.Some scholars have also constructed a multivariate grey relational model by controlling the weight of relevant factors and adjusting the sequence of relevant factors to render the shape similar to the system’s behavioral sequence[7].Furthermore,some researchers have extended the application of the GRA model to matrix sequences data[8-9],panel data[10-11],categorical variables[12],and multiperiod variables[13].

To summarize,recent improvements to Deng’s GRA model exhibit certain characteristics.First,most scholars have focused on improving the metric space measurement method based on various interpretations of a “relation”.Second,some new models have abandoned the point set topological space as a reference system for comparison,leading to the violation of axioms such as integrity and even-pair symmetry.While most models still adhere to the normative axiom,they assume that relevant factors and system behavior exhibit a direct incidence relationship.However,some relevant factors may exhibit an opposing trend to the system behavior,which these models are unable to recognize.

Recent research has proposed a new stream of analysis called inverse relational analysis to address the issues in existing models,as mentioned in the previous paragraph[1].However,earlier models,such as the grey periodic relational model[14]and the grey dynamic trend relational model[15],have also addressed the issues by breaking the normative axiom to incorporate inverse incidence relationships.These models calculate the grey relational degree based on the relational coefficients of points.The direction of incidence is determined by the increment in relevant factors and the system behavioral sequence at each data point.When the increment in the relevant factor has the same sign as that of the system behavioral sequence,it is considered a direct incidence relationship and an inverse incidence relationship is established otherwise.

However,these models have two main shortcomings.First,they focus only on the partial incidence direction of each data point,which ignores the holistic idea of GRA and is susceptible to random disturbances,leading to inaccurate judgments on the direction and strength of relevant factors.Second,the measurement method starts from the increment,which does not consider the absolute position of the data point.Consequently,when the incidence relationship of a point is inverse and the relevant factor increment direction is opposite to the system behavior increment,the distance between them may be shortened,making the model fail to satisfy the proximity axiom.In contrast,the bidirectional absolute GRA model recently proposed by Javed and Liu[16]overcomes these shortcomings.In this model,the incidence direction is identified by comparing the absolute grey relational degree of the original sequence with the absolute grey relational degree of the mirror sequence.The model extends the absolute GRA model and measures both the direction and strength of the relationship based on a holistic idea.Liu[17]also proposed a series of negative grey relational models; however,the incidence direction determination is based on the integration between the sequence and the axis without considering the relative trend between the related sequences.As a result,sequences considered to be in the same incidence direction may have completely opposite trends,which is a drawback.

The objective of this study is to devise a model that can recognize and measure the influence of inverse relevant factors within a system based on Deng’s GRA model.This model can be applied to all previous GRA problems and can recognize and quantify the inverse incidence relationship when it exists.When this relationship does not exist,the model’s calculations are identical to those of Deng’s GRA model.Our innovation lies in recognizing the presence of inverse factors while still preserving the systematic comparison advantages of Deng’s model.Specifically,we first expand the grey relational axiom to accommodate the inverse incidence relationship,then design a GRA model that incorporates these relationships and use the genetic algorithm to solve the model.Finally,we use the factor analysis affecting the quality of the innovation chain in Jiangsu Province,China,as an example to verify the feasibility and effectiveness of the proposed model and algorithm.

1 Construction of an Inverse Deng’s GRA Model

This section outlines the development of an inverse Deng’s GRA model,which is based on Deng’s GRA model through the extension of the axiom,model improvements,and algorithm design.The extended model uses an agenetic algorithm to identify the promotion or restriction relationships between the relevant factors and the system behavior.

1.1 Extension of the grey relational axiom

In the past,there have been in-depth discussions and analyses of Deng’s four axioms of GRA,including the even-pair symmetry axiom and integrity axiom[18-20].While the normative axiom has received less attention,it implicitly assumes that the incidence relationship in the system is direct.To incorporate the inverse incidence relationship in the axiom system,we propose an extension to the normative axiom that modifies the even-pair symmetry and integrity axioms.

Xi={xi(1),xi(2),…,xi(n)}

(1)

(2)

whereMiis a constant,and letMi=maxk{xi(k)},k=1,2,…,n.

Given real numbersγ(x0(k),xi(k)) andγ(x0(k),Mi-xi(k)),if the real numbers

(3)

(4)

satisfy the following four axioms:

1) Normative axiom.Letγ(X0,Xi) andγ′(X0,Xi) take values in the interval of[-1,1],where

γ(X0,Xi)∈(0,1],γ(X0,Xi)=1⟸X0=Xi

(5)

(6)

2) Integrity axiom.LetΓ(Xi,Xj)={γ(Xi,Xj),γ′(Xi,Xj)},Xi,Xj∈X={X0,X1,…,Xm},m≥2,where

(7)

3) Even-pair symmetry axiom.For anyXi,Xj∈X={X0,X1,…,Xm},m<2,there is

X={Xi,Xj}⟹Γ(Xi,Xj)=Γ(Xj,Xi)

(8)

4) Proximity axiom.The smaller the|x0(k)-xi(k)|,the larger theγ(x0(k),xi(k)).The smaller the|x0(k)-(Mi-xi(k))|,the smaller theγ(x0(k),Mi-xi(k)).

In this case,γ(X0,Xi) is referred to as the direct grey relational degree ofX0andXi,γ(x0(k),xi(k)) as the direct relational coefficient ofX0andXiat pointk.γ′(X0,Xi) is referred to as the inverse grey relational degree ofX0andXi,γ(x0(k),Mi-xi(k)) as the inverse relational coefficient ofX0andXiat pointk.The above four conditions are extended grey relational axioms,which extend the value of the grey relational degree to the interval of[-1,1].

1.2 Inverse Deng’s GRA model

Based on the extended grey relational axiom,the grey relational degree including inverse incidence relationships is designed.Let the incidence direction be represented by a vectorP={p1,p2,…,pm},and letpi(i=1,2,…,m) denotes the direct or inverse incidence relationship betweenX0andXi,such that

(9)

(10)

(11)

(12)

The grey relational coefficientγ(x0(k),xi(k)) and the grey relational degreeγ(X0,Xi) satisfy the extended grey relational axiom.In other words,the inverse Deng’s GRA model is an extension of Deng’s GRA model that accounts for inverse incidence relationships.

The main challenge is to determine the values of the elements in the incidence direction vectorP,which corresponds to the direct or inverse relationship between the relevant factors of the system and the system behavioral sequence.The value intervalCof the grey relational coefficient is dependent on vectorP,meaning that a change in the incidence direction of any relevant factor sequence may lead to a corresponding change in the grey relational degree of all sequences.Hence,determining the incidence direction of each relevant factor sequence is critical in accurately assessing the grey relational degree,including inverse incidence relationships.

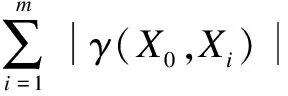
(13)

(14)

Similar to Javed’s confidence level scale[16],the proposed incidence direction confidence index is expected to be a valuable contribution to the theory of inverse GRA.

1.3 Model solving based on a genetic algorithm

The direct solution to the above optimization problem is challenging.The number of possibilities for the values of elements in vectorPincreases exponentially with the increase in the number of relevant factor sequences,making it computationally expensive.To reduce the computational cost,the agenetic algorithm is used.The genetic algorithm simulates the natural evolution process to search for the optimal solution.The algorithm starts with a set of initial solutions generated randomly and iteratively performs operations such as selection,crossover,and mutation to obtain the optimal solution.The computational flow of the genetic algorithm can be summarized as follows.

Algorithm1Solving inverse Deng’s GRA model based on the genetic algorithm

Input:X={X0,X1,…,Xm}.

Output:P={p1,p2,…,pm}.

① Individual coding.

② Population initialization.

③ Fitness evaluation.

④ Selection.

⑤ Crossover.

⑥ Mutation.

⑦ Satisfy termination criterion? If the criterion is met then returnP,otherwise back to ③.

Encoding is a method for converting the feasible solution to a problem from its solution space to a search space that can be handled by the agenetic algorithm.Based on binary coding (Formula 9),the vectorPcan be considered an individual in the genetic algorithm.

The initial population is a set of individuals.A set of initial vectorsPis randomly generated to form the initial population.Differences between individuals will lead to different levels of fitness.

The fitness function evaluates the ability of an individual to produce offspring.The higher the fitness,the stronger the ability to produce offspring.In this case,the objective functionf(p1,p2,…,pm) is considered as the fitness function:

(15)

The selection operator selects high-quality individuals based on their fitness and discards low-quality individuals,following the principle of “survival of the fittest”.The selection operator uses the roulette algorithm,where the probability of individual inheritance is proportional to its fitness.

The crossover operator involves exchanging some genes between two chromosomes that intersect each other in a certain way to create two new individuals.It is the primary method used to generate new individuals and determines the global search capability of the genetic algorithm.The crossover operator uses the random paired single-point crossover method,where a crossover point is randomly set in the individual code string,and the genes of the paired individuals are partially exchanged at this point.

The mutation operator is responsible for replacing genes at specific loci in the individual’s chromosome coding string with other alleles from the same locus,resulting in the creation of a new individual.It serves as an auxiliary method for generating novel individuals and plays a crucial role in the local search capability of the genetic algorithm.In this case,the mutation operator utilizes a single-point mutation approach,randomly selecting a locus within the individual for mutation.

The termination criterion determines whether the algorithm meets the conditions for calculation termination.In this case,the algorithm terminates when the number of iterations reaches the predetermined number of generations.

2 Application Case

In this section,an empirical study is conducted to evaluate the feasibility and effectiveness of the proposed inverse Deng’s GRA model.Specifically,the identification of key factors that affect the quality of the innovation chain in Jiangsu Province is considered an illustrative example.

2.1 System’s behavior and relevant factors

We developed a list of the factors that influence the quality of the innovation chain in Jiangsu Province based on two key dimensions: quality characteristics and innovation links.The factors are presented in Tab.1.

Tab.1 Relevant factors in the Jiangsu innovation chain

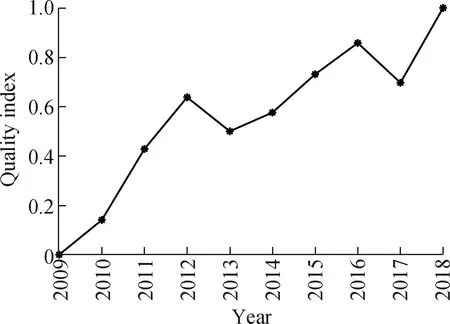
Tab.2 presents the system’s behavioral sequence and the relevant factor sequences of the quality of the innovation chain in Jiangsu Province between 2009 and 2018,expressed in the form of a quality index.

Tab.2 System’s behavioral sequence and relevant factor sequences

Fig.1 illustrates the development trend of the system’s behavior and relevant factors of the quality of the Jiangsu innovation chain.

(a)

2.2 Inverse Deng’s GRA and comparison with other models

To investigate the impact of each relevant factor on the quality of the Jiangsu innovation chain,we employed various grey relational analysis models,including Deng’s GRA model,absolute GRA model,bidirectional absolute GRA model[16],negative Deng’s GRA model[17],Pearson correlation coefficient,and the proposed inverse Deng’s GRA model.For these models,the distinguishing coefficientξ=0.5.Note that the Pearson correlation coefficient and the other models,except for Deng’s GRA and Liu’s absolute GRA models,can accurately determine the incidence direction.

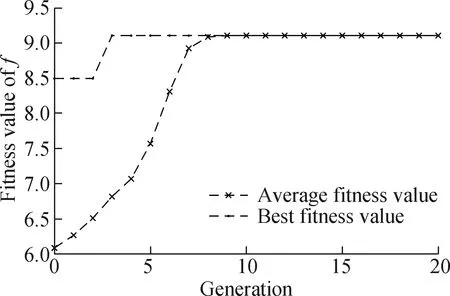
As outlined in Section 1.3,the proposed model can be solved using the genetic algorithm.Fig.2 depicts the changes in best fitness and average fitness of the population in the genetic algorithm of the inverse Deng’s GRA model as the number of iterations increases.The results indicate that the nonlinear constraint optimization problem with objective functionfconverges rapidly (see Fig.2(a)),with all individuals reaching the optimal solution in the ninth generation.Conversely,the objective functionf′ converges after approximately 200 generations (see Fig.2(b)).Furthermore,the optimal solution of the objective functionf′ is significantly higher than that off.

(a)

Tab.3 presents the results of the GRA models,as well as the Pearson correlation coefficient,sorted according to their absolute values.In contrast to the first two classical models,the other four models treat the knowledge innovation link of the process characteristicX4as an inverse relevant factor.However,the inverse Deng’s GRA model and Pearson correlation coefficient deem the relationship strength ofX4to be high,while the bidirectional absolute GRA model and negative Deng’s GRA model consider the strength of the relationship to be low.The Pearson correlation coefficient reveals a strong linear correlation of-0.905 betweenX4and the system’s behavioral sequence,raising doubts about the acceptability of the bidirectional absolute GRA model and negative Deng’s GRA model results.

Tab.3 Comparison of grey relational analysis models

In addition,the bidirectional absolute GRA model and negative Deng’s GRA model both analyzeX5as an inverse relevant factor.However,the bidirectional absolute GRA model deems this result insignificant (δi=0),while the negative Deng’s GRA model is unable to determine its significance.The inverse Deng’s GRA model,which considersX5as a direct relevant factor,also finds the result insignificant (Ti=0.998).Regardless ofX5’s classification as a direct or inverse relevant factor,its relationship strength is the weakest in any of the three models.

3 Conclusions

1) An inverse Deng’s GRA model is constructed along with the genetic algorithm.The model helps identify and quantify the promotion or restriction relationships between the factors and system behavior,thus providing insight into the system’s formation and change process.The proposed model expands the application of grey relational analysis and retains the excellent characteristics of Deng’s GRA model.

2) The inverse Deng’s GRA model can effectively identify and quantify inverse relationships.In the case analysis of the quality of Jiangsu’s innovation chain,the inverse Deng’s GRA model identifies the knowledge innovation link of the process characteristic as the inverse relational factor of the Jiangsu innovation chain quality,with a relational degree of-0.815.Compared to the existing models,the inverse Deng’s GRA model is more effective in identifying the incidence direction and strength of relevant factors in the grey system.

3) As a relatively new research direction,there is considerable potential for further development of inverse relational analysis.First,it is necessary to propose additional inverse relational analysis models to expand the application scope.Second,there is a need for uniform judgment criteria for the incidence direction and strength among various models,which is currently a challenge that requires further exploration and solution.