合理设置问题链，打造高效数学课堂

程斌 沈占立

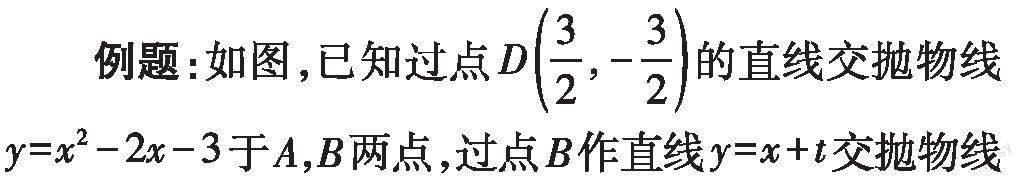
提问是课堂教学中常用的一种教学手段.合理的问题，能有效地启发学生的思维，激发其学习兴趣，提升课堂教学的效率.在一堂课中，可能会需要设置多个课堂问题，我们就要思考如何将这些问题串联起来，才能让学生在解决问题的过程中获得新知识、积累经验，培养其创造性思维、批判性思维、发散性思维.

一、由易到难，设置层层递进的问题链

在设置递进式的问题链时，一方面要“以旧引新”，从学生原有的认知结构出发，逐步引出新的问题，建立起各个问题之间的联系；另一方面要从简单的问题入手，层层深入，再逐步加大问题难度，使其呈螺旋式层层递进，以引导学生逐步解决问题，帮助其建立完整的知识体系.

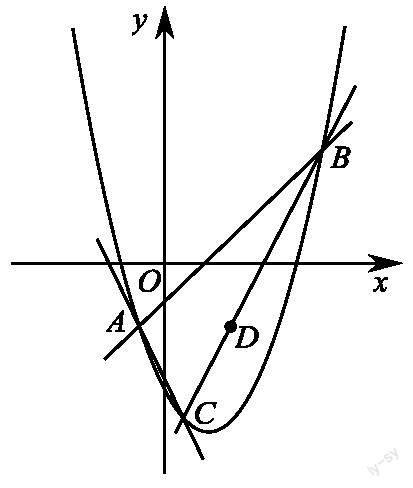
于点C.求证：直线AC恒过定点.

问题3：如何求直线AC的方程？

学生通过递进式的问题链，逐步求得直线AC恒过的定点，并掌握解答此类问题的一种思路：根据抛物线的方程先设出点的坐标，再求直线的方程，即可利用消元思想求定点的坐标.

二、以点带面，设置环环相扣的问题链

在设置问题链时，教师要将问题串相互关联起来，由点到面、由面到体，围绕核心问题和教学目标设置出一系列具有逻辑性的子问题，并将其以一定的顺序排列出来，使其环环相扣，以使学生能借助问题串，将所学的知识关联起来，通过思考前面的问题，推导出后面问题的答案.这样便能有效地启发学生的思维，培养其数学思维能力.

以上述例题为例.为了启发学生的思维，使其通过自主思考找到解题的思路，笔者设置了如下的问题链：

问题1：怎样根据抛物线的方程设点A、B、C的坐标？

答：设A（a，a2-2a-3），B（b，b2-2b-3），C（c，c2-2c-3）.

問题2：怎样求得直线AB、BC、AC的方程？

答：利用待定系数法可求得直线AB的方程为y=（a＋b-2）x-ab-3；直线BC的方程为y=（b＋c-2）x-bc-3；直线AC的方程为y＝（a＋c-2）x-ac-3.

问题3：怎样说明直线AC：y＝（a＋c-2）x-ac-3恒过定点？

答：把-ac-3用含a＋c-2的式子表示.

问题4：怎样简化直线AC的方程？

这些问题环环相扣，逻辑紧密，学生通过“复盘”，便可明确：求解直线恒过定点问题的一般方法，是先求出直线的方程，再将其与抛物线联立，用含k的式子表示b.

总之，在设计课堂问题时，教师要围绕某一个题目、主题、知识点来设置一些问题，借助环环相扣、层层递进的问题链来引导学生进行深入思考，开展深度学习.