蛮力法、分治法和动态规划法求解最大子数组问题的思考

陈 艳，文晓棠

（广州华商学院数据科学学院，广州 510520）

0 引言

最大子数组问题是一个众所周知的算法问题，在计算机科学、金融和工程等各个领域都有许多实际应用。这个问题涉及到在一维数字数组中找到具有最大和的连续子数组。有几种方法可以解决这个问题，包括蛮力算法、分治算法和动态规划算法［1］。在本文中，对这些方法进行了比较，并提供了实验结果来分析它们的性能。本研究的目标是确定解决最大子数组问题的最有效方法，并全面了解用于解决该问题的不同算法。

1 问题概述

假如我们有一个数组，数组中的元素有正数和负数，如何在数组中找到一段连续的子数组，使得子数组各个元素之和最大。

定义：数组中连续的一段序列称为子数组。

定义：数组中元素和最大的非空子数组称为最大子数组。详细定义为：

输入：给定一个数组X［1，2，…，n］，对于任意数组下标为l，r（l≤r）的非空子数组，其和记为S（l，r）

输出：求S（l，r）的最大值，记为Smax。

比如已知序列X=（-2，2，5，-7，-1，2，-4，3），求序列的最大子数组，正确的答案为X［2，3］，子数组和为7。本文将以此序列为例全面分析各种不同算法解决此问题。

2 蛮力算法

蛮力算法也称为穷举法或暴力法，它是算法设计中最常见的方法之一。蛮力算法的基本思路是对问题的所有可能状态一一测试，直到找到解或将全部可能状态都测试为止。蛮力法是一种简单、直接地解决问题的方法，通常直接基于问题的描述和所涉及的概念定义来解决问题。蛮力算法是基于计算机运算速度快这一特性，在解决问题时采用的一种“懒惰”策略。蛮力算法是学习算法的基础，很多算法的优化都是在蛮力算法的基础上进行的，因此想要熟练应用各种算法策略，培养算法思维，必须对蛮力算法有深刻的认识和熟练的应用。

蛮力算法是解决最大子数组问题的一种简单方法。它包括生成所有可能的子数组并计算它们的和。然后，返回具有最大和的子数组。已知序列如图1所示。

图1 序列X

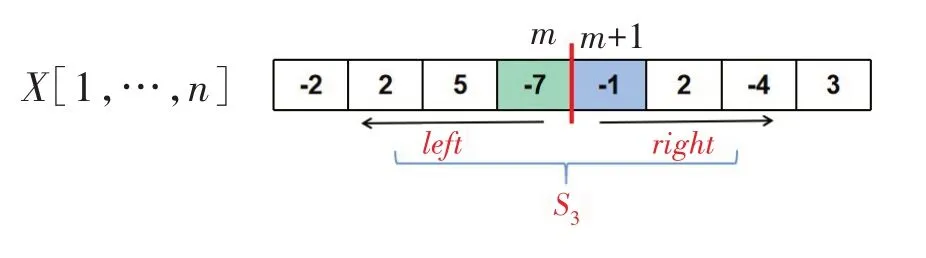
图2 求S3的思路

遍历子数组X［l，2，…，r］的下标，l的取值范围：1～n，r的取值范围：l～n，遍历过程中对子数组元素求和，并记录最大值Smax。

算法伪代码如下：

该算法的时间复杂度为O（n3），因为它需要生成n2个子数组并计算它们的和。

3 优化的蛮力算法

根据上述算法，当求S（i,j）时，通过来得到，求S（i，j+1）时，通过来得到，通过观察发现，S（i，j+1）的求解包含着子问题S（i,j）的求解，如果能利用S（i,j）的解来求解S（i，j+1），则能改进算法的效率。以此为优化的目标，设计优化的蛮力算法如下：

通过上述改进，减少了一层循环的应用，算法的复杂度由O（n3）降为O（n2），效率提高了一个数量级。

4 分治法

分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同［2］，求出子问题的解，通过合并的方式就可得到原问题的解。用分治法求解的问题具有如下基本特征：①该问题的规模缩小到一定的程度就可以容易地解决；②该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；③利用该问题分解出的子问题的解可以合并为该问题的解；④该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

分治法求解问题的基本步骤分为三步［3-4］：

第一步：分解原问题。将原问题分解为两个或多个与原问题性质相同、规模更小的子问题，不同的问题分解的策略不一样，比如二路归并排序的分解策略是一分为二，快速排序的分解策略为利用数组划分算法实现分解。

第二步：求解子问题。对子问题的求解分别调用一次递归即可，因为子问题本质上和原问题性质相同，只是规模变小而已。

第三步：合并子问题的解。通过对子问题的解进行合并，可以得到原问题的解。此步反映了分治法具有最优子结构的性质，即原问题的解可以通过子问题的解组合得到。不同的是，对子问题的解合并方式不一样，比如归并算法需要有专门的合并算法来实现，而快速排序却没有严格意义上的合并过程。

分治算法是解决最大子数组问题的一种有效方法。该算法递归地将输入数组分为两半，得到两个子问题，分别解决每个子问题的最大子数组问题，再求出跨左右两个子问题的最大子数组，然后将解组合起来，由此得到原始数组的最大子数组。按照分治法解决问题的基本步骤具体设计思想如下：

（1）分解

将数组X［1，2，…，n］分为和从中间分成两半，得到两个子问题，即求解数组的最大子数组问题和求解数组的最大子数组问题。

（2）求解

递归求解上述两个子问题，将结果分别记为S1，S2。

（3）合并

两个子问题的解S1，S2可能是原问题的解，也可能不是原问题的解，因为还存在一个跨左右两个子数组的最大子数组，记为S3。S3有个特点，它一定是包含左边子问题的最后一个元素和右边子问题的第一个元素，即跨中间点的最大子数组。不难理解，原问题的解在S1，S2和S3中，为Smax=max｛S1,S2,S3｝。显然关键问题是求S3。

对于S3的求解，可以用蛮力法，但效率低，达到O（n2）的规模。设左边子问题的最后一个元素下标为m，则右边子问题第一个元素下标为m+1，如果分别求解出左边以元素X［m］结尾的最大子数组，记为left；求出右边以元素X［m+1］开始的最大子数组，记为right，则可顺利求出S3=left+right。见图。

以此为思路，设计求S3的算法getS3（X，low，mid，high），伪代码如下：

算法中，求left的复杂度为O（mid），求right的复杂度为O（n-mid），则求S3的算法复杂度为O（n），显然比直接蛮力法求S3的效率要高一个数量级。

分治法求解最大子数组问题的主算法Max-SubArray（X，low，high）伪代码如下：

5 动态规划法

动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，然后从这些子问题的解得到原问题的解［3］。与分治法不同的是，适合于用动态规划求解的问题，经分解得到的子问题往往不是相互独立的。也就是各个子问题包含公共的子子问题［4］。为了解决子问题重复计算的问题，动态规划算法对每个子问题只计算一次，不管该子问题是否以后被用到，都将其结果保存到一张表中，从而避免每次遇到各个子问题时重新计算答案［5］。动态规划通常应用于求解最优解问题，如0-1背包问题，最大子数组问题，矩阵链乘法问题等。

动态规划法所能解决的问题一般具有以下几个特征：①大问题可分解性。该问题可以分解为若干个规模较小的问题，即该问题具有最优子结构性质；②子问题易解决性。该问题的规模缩小到一定的程度就可以容易地解决；③解可合并性。利用该问题分解出的子问题的解可以组合为该问题的解；④子问题重叠性。当计算出某个子问题的解时，后续多个问题都需要计算该子问题的解，所以计算出某个子问题的解，并将其保存，就节省了分治法重复计算的时间。

动态规划算法求解问题的基本步骤分为四步：

第一步：问题结构分析。分析问题的特点，结合问题的特点分析问题的结构，找到合适的办法来表示问题，进而通过此表示方法来表示原问题。

第二步：递推关系的建立。动态规划算法的核心是填表，表中每个单元格代表一个子问题的解，每个单元格的解是通过其他子问题的解组合得到的，即动态规划算法也要满足最优子结构的性质。因此要分析子问题之间的依赖关系，也即分析最优子结构性质，由此得到子问题求解过程的组合方式，即递推关系。

第三步：确定计算顺序。对于填表的办法，不同的问题填法不一样，有的表从左向右自上而下来填，有的表需要从后往前填，有的甚至按对角线的方式从左向右填，具体的填表方式因问题性质而异，需要通过第二步得到的子问题间的递推关系来确定。

第四步：最优方案的追踪。通过第三步得到了问题的最优值，对应的最优方案可以通过记录填表时的决策过程，通过回溯的方式来得到。

动态规划算法是解决最大子数组问题的另一种有效方法。该算法以数组中的每一个元素作为一个子数组的最后一个元素，向前遍历求和。通过规律观察发现，如果此元素的前一个子数组和为负，则以这个元素为最后一个元素的子数组的最大和为此元素本身；如果此元素之前的子数组和为正，则以这个元素为最后一个元素的子数组最大和为此元素本身加上前一个最大子数组和。每做一次子数组求和，就与前面出现的最大和作比较，如果此子数组大于前面的最大子数组，就将其赋值给最大值。若定义D［i］表示以X［i］结尾的最大的子数组和，则D［i］的求解如图3所示。

图3 求解D［i］的思路

按照此思路，根据动态规划算法求解问题的基本步骤，设计如下：

问题结构分析：

定义D［i］：表示以X［i］结尾的最大的子数组和，则原问题表示为Smax=max｛D［i］｝（1≤i≤n）。

递推关系建立：

根据递推关系的分析，D［i］实际上是一张一维表，故将原问题转换为填D这张表的问题，如图4所示。

图4 表D的结构

计算顺序：

根据递推式，将两个子问题D［i］和D［i-1］在表中的位置关系表示出来，如图5所示，通过观察发现要求D［i］，需要先求D［i-1］，则得到此表的计算顺序为从左到右的顺序，原问题的解在表中的某个位置。如图6所示。

图5 D［i］和D［i-1］在表中的位置关系

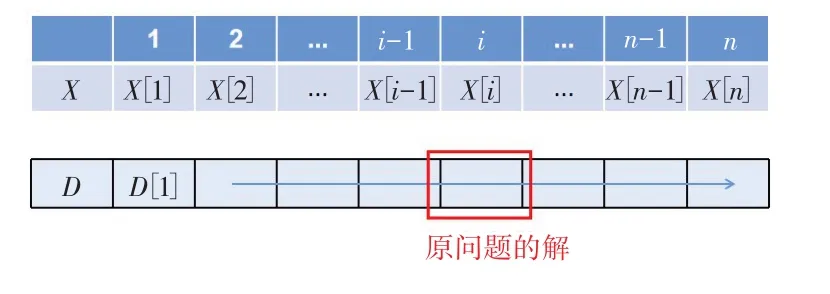
图6 计算顺序

以此为思想，设计算法MaxSubjectarrayDP（X，n）伪代码如下：

该算法用一层循环实现，时间复杂度为O（n），因为它在输入数组中迭代一次，在恒定时间内解决每个子问题。

6 算法对比实验

按上述设计实现这三种算法，并进行对比测试。首先生成一些随机数数组，数组规模从100 到100000000 不等。然后对每个数组运行优化的蛮力算法、分治算法和动态规划算法，并计算它们所需的时间。测试结果见表1。

表1 实验数据

实验结果表明，对于较大的输入大小，动态规划算法优于蛮力算法和分治算法。例如，对于大小为100000 的输入数组，蛮力算法需要1 s 以上的时间来计算最大子数组，分治法需要1 ms，动态规划法需要3 ms，此时，动态规划法无优势；但数组规模到1000000，蛮力法已经不是秒级，程序运行时几分钟之内未出结果，分治法18 s，动态规划只需1 ms；数组规模到10000000 时，动态规划法的优势更明显，且随着数组规模的增大，动态规划的优势不断增大。由此可见，分治算法比蛮力算法表现更好，但对于较大的输入大小，仍然比动态编程算法花费更长的时间。

7 结语

本文比较了解决最大子数组问题的不同方法，包括蛮力算法、分治算法和动态规划算法。实验结果表明，动态规划算法是解决这个问题的最有效方法，特别是对于大输入量的情况。分治算法也是一个很好的替代方案，但它不如动态规划算法有效。蛮力算法是一种基本的方法，只能应用于较小的输入大小。总体而言，动态规划算法为最大子数组问题提供了最优解，其时间复杂度为O（n）。