随机Navier-Stokes方程的两重网格有限元方法研究
刘 倩, 李 剑
(陕西科技大学 文理学院, 陕西 西安710021)
Navier-Stokes(N-S)方程[1-4]描述的是粘性不可压缩流体动量守恒的运动方程,反映了粘性流体流动的基本力学规律,是粘性不可压缩流体的经典模型。为了使模拟结果更好地反应实际情况,在相应的确定性系统中添加了一个具有随机性且依赖于解的噪声项,所得方程被称为随机Navier-Stokes方程。

为了进一步更加高效地求解随机N-S方程,应用两重网格算法[10-14]。两重网格算法已经广泛应用在线性和非线性椭圆边值问题,Xu[10-11]引领了它的发展,Girault[12]以及Li[13]等使两重网格算法已经扩展到稳定的N-S方程,使得理论更加完善。该方法的优点在于,若在粗细网格之间选取适当的比例,则两重网格算法的收敛速度与通常的稳定有限元方法相同的前提下可以节省大量的CPU时间。
本文主要研究伴随乘性噪声随机N-S问题的Oseen两重网格有限元算法。研究的方法是基于文献[7]和Oseen迭代技术的两重网格算法[14],即在Euler-Maruyama方法和Taylor-Hood有限元方法的基础上应用Oseen两重网格算法求解随机Navier-Stokes问题。我们在稳定性条件的假设下提出误差分析,结果表明两重网格有限元方法可以与传统有限元方法保持相同的误差阶,并且能节省可观的计算量,最后通过数值实验同样证实了理论分析的结果。
1 随机Navier-Stokes方程
假设空间D是R2中具有Lipschitz连续边界的有界开集,考虑DT=[0,T]×D的随机Navier-Stokes方程:
(1)
divu=0 inDT
(2)
式中:μ表示粘性系数;u=(u1,u2)表示速度场;p表示压力场;f表示外力;{W(t),t≥0}表示Wiener过程。在DT中,我们赋予初始条件和Dirichlet边界条件:
u(0)=u0inDT
(3)
u= 0 on ∂DT
(4)
首先我们介绍空间符号,(Ω,F,{Ft},P)是伴随σ代数{Ft}和概率测度P的概率空间,定义在概率空间的随机变量v,E[v]表示其期望。对于伴随范数‖·‖X的赋范线性空间V,定义Bochner空间:
(5)
以及其范数:
(6)
进一步介绍离散的空间符号,即定义有限元空间:
(7)
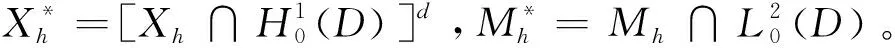
引入双线性形式:
(8)
和三线性形式:∀u,v,w∈X,
(9)
三线性形式有以下性质:
b(u,v,w)=-b(u,w,v)
(10)
(11)

(12)
对于任意的(u,p)∈(D(A)∩X,H1(D)∩M),
其Stokes投影算子满足:
(13)
最后为了对随机项B(·,u)dW作出解释,本文分别给出Wiener过程W,随机积分的定义和性质,以及问题(1)的变分弱解形式。
定义1.1 设Q是L2(D)到其本身的非负对称线性算子,假设Q具有一组本征值和本征函数{(λj,qj)}j≥1,其中{qj}j≥1是L2(D)的正交基。如果{βj(t),t≥0}j≥1是独立同分布适应{Ft}的实值Wiener过程序列,则定义在(Ω,F,{Ft},P)上的L2(D)值Wiener过程{W(t),t≥0}定义为:
(14)
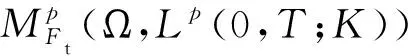
(15)
(16)
定义1.3[16]设u0∈L2(Ω,X0)和f∈L2(Ω,L∞([0,T];[L2(D)]d)),对任意(v,q)∈(X,M)和(u,p)∈L2(Ω,L∞(0,T;X)∩L2(0,T;X)∩C(0,T;Y))×L2(Ω,L2(0,T;M)),随机过程{(u(t),p(t)),0≤t≤T}是方程(1)的弱解是指:
(17)
且d(u,q)=0。
2 假 设
2.1 算子B的假设
假设算子B:[0,T]×[L2(D)]d→L2(Ω,K)是Hölder-Lipschitz连续并且在第二个参数上具有线性增长,即对于任取的u,v∈[L2(D)]d和s,t∈[0,T],都存在一个常数C3>0,使得:
‖B(s,v)-B(t,w)‖≤
C3(1+‖v‖L2)
(18)
2.2 随机inf-sup条件[7]
(19)
2.3 时间半离散Euler-Maruyama格式[7]
令N是正常数,其中n=0,1,…,N,τ=T/N且tn=nτ,设u0=u0,则式(2)的Euler-Maruyama时间离散格式即对于任意的(v,q)∈(X,M),求解{(un,pn)∈L2(Ω,X)×L2(Ω,M):0≤n≤N}使得满足:
(20)
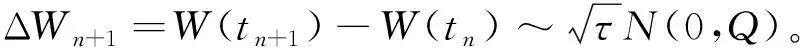
2.4 时间半离散稳定性估计{7}
根据Euler-Maruyama时间半离散格式(20),随机过程{(un,pn)∈L2(Ω,X)×L2(Ω,M),0≤n≤N}满足下列稳定性估计:

(21)
(22)
式中C4是独立于τ的正常数。
2.5 空间离散稳定性估计{7}
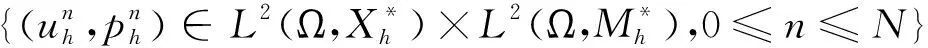
满足下列稳定性估计:
(23)
(24)
式中C5是独立于τ和h的正常数。
2.6 时间半离散的误差估计{7}
离散过程{(un,pn);1≤n≤N}满足下列误差估计:
(25)
(26)
式中C6是独立于τ的正常数。
2.7 空间离散的误差估计{7}
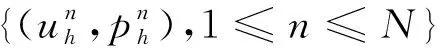
(27)
(28)
式中:C7是独立于τ和h的正常数。
3 两重网格算法
在本节中,文章利用Oseen两重网格算法求解伴随乘性噪声的随机Navier-Stokes方程。
1) 求解粗网格上的随机Navier-Stokes方程
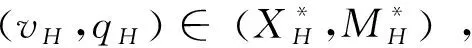
(29)

2) 求解细网格上的随机Stokes方程
对于任意的(vh,qh)∈(Xh,Mh),求解逼近解

(30)

为简便起见,令
接下来基于稳定性估计式(21)~(24),利用Oseen两重网格算法可得优化误差估计,首先考虑速度的误差估计。
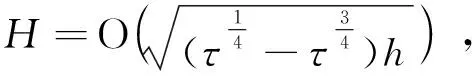
(31)
式中:C=C*(C2,C6,C8)是独立于τ和h的正常数。
证明:式(23)减去式(21),依据条件(2),并且令vh∈X0,选取vh=en+1,对于任意n≥1得到以下误差方程:
(32)

(33)
在假设2.1中算子B的条件下,根据鞅的性质,式(13),式(16)和Young不等式,式(32)的随机项可以被控制为:
(34)
最后,利用离散Gronwall引理整理得出以下结论:
(35)
由式(21),式(21)和式(35),利用三角不等式,可得:
(36)
定理证毕。
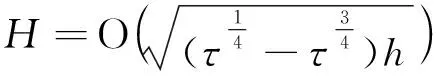
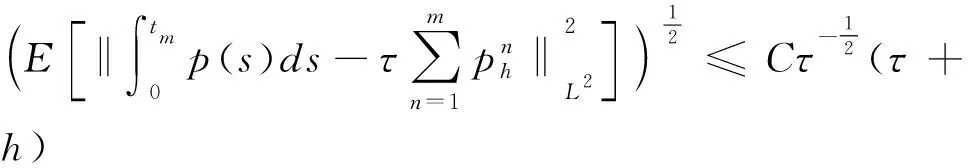
(37)
式中:C=C*(C2,C6,C9)是独立于τ和h的正常数。
证明:令式(24)减去式(22),取期望及求和(1≤n≤m(m≤N))整理可得:
(38)
由于随机离散inf-sup条件,针对式(38)右边的每一项进行控制,前三项应用Young不等式,在定理1的误差估计下,对非线性项运用式(11),式(21)和式(22)收敛,由假设2.1以及式(13)~(16)对随机项进行控制可以得到:
C9τ-1H2
(39)
式中C0是Poincare不等式的常数。
最后,由式(13),式(26)和式(39)利用三角不等式得:
(40)
4 数值算例
1) 算例1
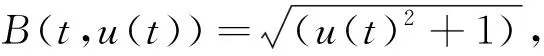
(41)

gj(x,y)=(c(sin(jπx)+(jπx)3),c(sin(jπy)+(jπy)3))
(42)
在本次测试中,我们使用以下参数:c=0.1,T=1,μ=0.1,M=10,Nm=1000,τ0=0.001,h0=1/100进行数值模拟。
令τ0和τ分别表示用于生成解析真解和数值解,显然τ0≪τ。另外,对于任何1≤n≤N,我们使用以下数值积分公式计算误差:
(43)
(44)
(45)
为了验证时间收敛速度,我们固定h=1/100,并使用不同的时间步长τ=0.01,τ=0.02,τ=0.04,τ=0.08来估计速度时间近似的L2(AUn)和H1(BUn)范数误差和压力的H1(BPn)范数误差,表1和表2说明了分别使用单层有限元方法和Oseen两重网格算法所得到的速度和压力近似的收敛速度。 其中速度误差是在强范数下测量的,压力误差是在时间平均范数下测量的,数值结果清晰地验证了误差分析预测的半阶收敛速度。

表1 单层网格有限元方法近似解的时间离散误差Tab.1 Time discretization errors of the approximate solutions by one-level finite element method

表2 两重网格有限元方法近似解的时间离散误差
为了验证空间收敛速度,我们固定τ=0.005,并采用不同的空间网格尺寸h=1/20,h=1/40,h=1/80来估计速度空间近似的L2(AUn)和H1(BUn)范数误差和压力的H1(BPn)范数误差,表3和表4显示了分别使用单层有限元方法和Oseen两重网格算法在不同空间尺寸h产生的空间离散的收敛速度。显然,空间收敛速度与理论预测一致,保持一阶的收敛阶。

表3 单层网格有限元方法近似解的空间离散误差Tab.3 Spatial discretization errors of the approximate solutions by one-level finite element method

表4 两重网格有限元方法近似解的空间离散误差Tab.4 Spatial discretization errors of the approximate solutions by two-level finite element method
为了说明Oseen两重网格算法的高效性,分别运用算法1和算法2求解随机Navier-Stokes方程,以此来比较两种方法的求解时间,通过表5的结果可以发现,在保证误差精度与收敛阶的前提下,双重网格算法能够节省大量时间,减少成本,如果网格剖分加细,这种效果会更加明显,算法的优越性会更加明显,在随机偏微分方程求解方面具有很好的现实意义和实用价值。
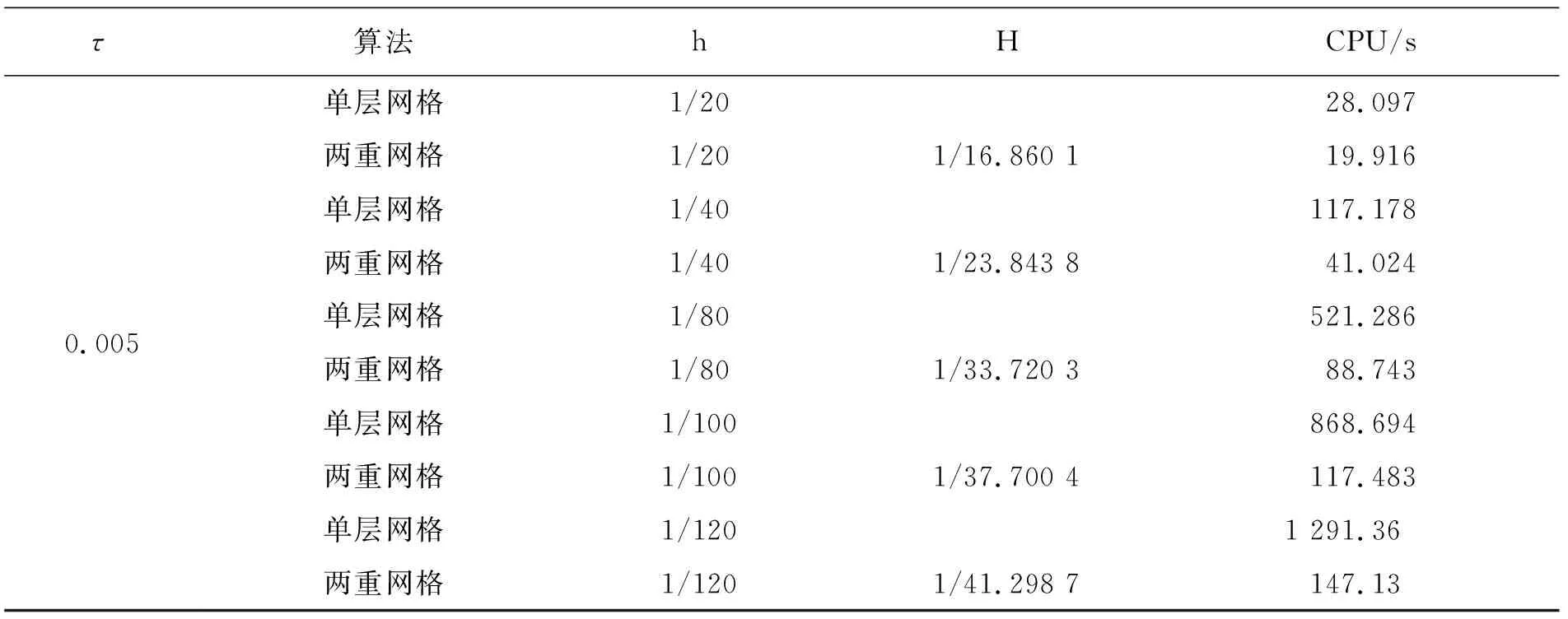
表5 单层网格与两重网格算法CPU性能比较Tab.5 Comparison of CPU between one-level method and two-level method
2) 算例2
在第二个数值实验中,我们计算了单位平方区域D=(0,1)2的驱动方腔流动,选取f=(0,0),无滑移边界条件只施加在速度u=(1,0)的边界{(x,1):0 本文针对伴随乘性噪声的随机Navier-Stokes方程,基于时间离散Euler-Maruyama格式和Taylor-Hood有限元空间离散基础上,提出相对应的Oseen两重网格算法,并进行了理论分析和数值模拟。 Oseen两重稳定有限元法是求解二维非定常随机Navier-Stokes方程的高效方法。表明了Oseen两重网格有限元方法对求解随机Navier-Stokes方程具有可行性和高效性,它也适用于解决流体力学中的一些实际工程问题。 此外,这些方法还可用于求解二维和三维随机不可压粘性流动,这将在以后的工作中讨论。5 结 论

