基于改进HHO算法的碳交易价格组合预测研究
赵 峰, 徐丹华
(安徽工业大学 管理科学与工程学院, 安徽 马鞍山 243032)
我国碳交易已经拥有一定规模且市场前景广阔[1-2]。碳价格在促进“双碳”目标实现的基础上具有一定的负面影响[3],如何通过碳交易价格引导投资者更好地利用碳排放权交易市场进行投资,推动市场的理性发展,已成为问题的关键。
目前,国内外学者不断对碳交易价格及其影响因素进行研究和分析,并尝试建立模型对碳交易价格进行预测。有关碳交易价格预测的研究主要涉及两个方面。
1) 针对碳交易价格的时间序列建立预测模型。文献[4]~[8]通过对碳价时间序列进行分解、重组,分别对重组后的序列建立不同的模型进行碳交易价格预测。Zhang等[9]提出了一种先进的深度神经网络模型来预测碳价格。Xu等[10]利用时间序列复杂网络分析技术和极限学习机算法提出了一种新的碳价预测模型。Yang等[11]提出了包括改进数据特征提取技术,建立LSTM、CNN、ELM预测子模型及多目标优化算法加权策略的集成预测系统(EPS)。彭武元等[12]针对碳价格时间序列,建立了马尔科夫转换多重分形模型。Zhang 等[13]提出了一种整合 PSO 和多输出支持向量回归(MSVR)的混合方法来预测碳价格。蒋锋等[14]基于混沌粒子群优化(CPSO)算法提出了一种优化的BP神经网络碳价格预测模型。
2) 针对碳价波动的相关因素建立预测模型。Xie 等[15]创新性地使用文本在线新闻来构建与气候相关的变量,并结合其它变量利用长短期记忆网络和随机森林模型对碳价进行预测。刘金培等[16]对非结构化数据、结构化数据和碳交易价格分别进行分解、重组,建立了自回归积分滑动平均模型、偏最小二乘回归和神经网络模型。魏宇等[17]对影响我国碳价格的相关因素进行了分析,筛选出9个重要影响因素,并对各类经典预测模型进行对比分析。
通过相关文献分析发现,针对国内碳交易价格预测的文献相对较少,且大部分文献仅从碳交易价格本身或碳交易价格相关影响因素着手进行建模预测,目前尚没有综合考虑两种建模方法的相关文献。因此,本文综合考虑以上两个方面,分别建立CEEMDAN-ARIMA-指数平滑模型和改进的哈里斯鹰优化极限学习机的碳价格预测模型,并通过lp范数建立组合预测模型。为此,论文在现有文献的基础上,构建了基于lp范数的碳交易价格组合预测模型。该模型具有如下创新性:
1) 为了充分挖掘碳交易价格所带来的信息,一方面考虑碳交易价格本身建立了CEEMDAN-ARIMA-指数平滑模型,另一方面考虑碳交易价格的经济指标和技术指标等建立了THHO-ELM模型;
2) 利用多策略融合改进的哈里斯鹰算法优化极限学习机模型中的权值和阈值,并利用优化后的模型对广东省碳交易价格进行训练和预测;
3) 为充分利用上述两个模型的优势,建立了基于lp范数的误差平方绝对值模型。实证结果表明,本文提出的lp范数组合预测模型优于单一的分类模型,对碳交易价格预测精度较高。此外,本文在我国的东、中、西部分别选取上海、湖北和重庆碳交易试点进行预测,进一步验证了模型的可靠性。
1 理论基础
1.1 完全自适应噪声集合经验模态分解
经验模态分解(empirical mode decomposition, EMD)是处理非平稳信号的方法之一,其本质是将原始的复杂信号分解成包含原始信号部分特性的多个IMF分量和残余分量之和[18]。EMD算法虽对信号具有一定的适应性,但易产生模态混叠现象,从而影响信号分解质量。而完全自适应噪声集合经验模态分解(CEEMDAN)加入了经EMD分解后含辅助噪声的IMF分量,并对分解得到的IMF分量进行总体平均,完美解决了EMD算法中存在的模态混叠现象。
CEEMDAN算法的实现步骤:


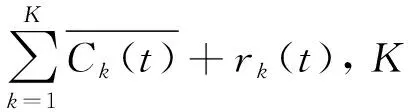
1.2 哈里斯鹰优化算法
1.2.1传统的哈里斯鹰优化算法
哈里斯鹰算法(harris hawks optimization, HHO)是基于哈里斯鹰的群体捕食行为而提出的一种元启发式算法[19],主要包括探索阶段、探索到开发的转换以及局部开采三个阶段。每个阶段的具体描述如下。
阶段1:探索阶段哈里斯鹰的位置更新:
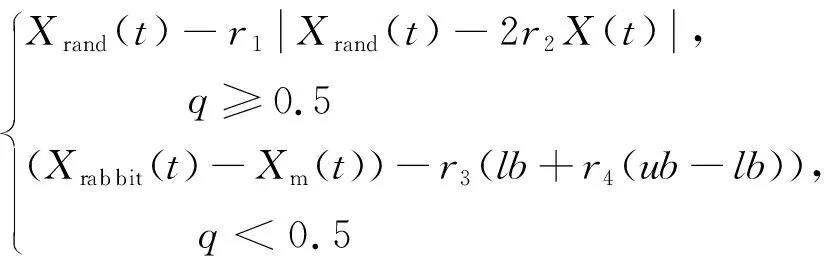
(1)
式中:q、r1、r2、r3、r4均为[0,1]内的随机数;ub、lb为搜索空间的上、下界;Xrand为群体内随机个体位置;Xrabbit为猎物位置;Xm为种群内所有个体的平均位置。
阶段2:探索到开发的转换:
(2)
式中:E0为初始状态的逃逸能量,在算法迭代过程中于[-1,1]之间随机变化;t为种群当前迭代次数;T为种群的最大迭代次数。
阶段3: HHO算法根据哈里斯鹰的围捕方式和猎物的逃脱行为,提出了四种攻击策略。
策略1:当逃逸能量|E|≥0.5且随机数r≥0.5时,哈里斯鹰采取软围攻策略。其位置更新为:
X(t+1)=Xrabbit(t)-X(t)-E|JXrabbit(t)-X(t)|
(3)
式中:J=2(1-r5)为猎物的跳跃距离;r5为[0,1]内的随机数。
策略2:当逃逸能量|E|<0.5且随机数r≥0.5时,哈里斯鹰采取硬围攻策略。其位置更新为:
X(t+1)=Xrabbit(t)-E|Xrabbit(t)-X(t)|
(4)
策略3:当逃逸能量|E|≥0.5且随机数r<0.5时,哈里斯鹰采取渐进式快速俯冲软包围。其位置更新为:

(5)
式中:S为随机行向量;D为解决问题的维度;LF为levy函数。
策略4:当逃逸能量|E|<0.5且随机数r<0.5时,采取渐进式快速俯冲硬包围。其位置更新为:
X(t+1)=
(6)
1.2.2改进的哈里斯鹰优化算法
传统的HHO算法与其他群智能优化算法一样,在求解复杂优化问题时,存在易陷入局部最优且收敛精度不高等缺点。针对以上问题,文献[20]引入了指数能量方程、正弦逃逸距离方程、柯西变异和Circle混沌扰动对传统的HHO算法进行改进,改进的哈里斯鹰算法记为THHO。
1) 指数能量方程
逃逸能量E的取值决定了种群是进行探索还是局部开采,但在传统的HHO算法中E是通过线性递减进行更新,即在迭代后期种群只进行局部开采,这使得算法易陷入局部最优,因此本文对E作如下改进:
(7)
E=E0×(2×r6-1)
(8)
式中:c为常数2;r6为[0,1]之间均匀分布的随机数。
2) 逃逸距离方程
猎物逃逸能量E的变化必然会引起其在逃跑过程中跳跃距离J的变化,因此设置J的取值如下:
3) 柯西变异和Circle混沌扰动
柯西变异来源于连续型概率分布的柯西分布,主要特点为零处峰值较小,从峰值到零值下降缓慢,可使变异范围更均匀。在种群个体位置更新中引入柯西变异,提升算法的搜索能力。变异公式为:
mutationX(t)=X(t)(1+tan(π(u-0.5)))
(10)
式中:mutationX(t)为个体经过柯西变异后的位置;X(t)为个体原来位置;u为区间[0,1]内的随机数。
混沌扰动可增强算法的全局搜索能力。在全局探索和局部开采后,对种群中适应度值较高的个体进行Circle混沌扰动,与柯西变异同时发挥作用,以增加种群的多样性,防止陷入局部最优。

(11)
式中:CircleX(t)为个体经过混沌扰动后的位置;X(t)为个体原来位置;a为常数0.5,b为常数2.2。
1.3 lp范数
设J表示基于lp范数的误差绝对值之和,则:
(12)
式中:et为第t时点组合预测的误差;eit为第t时点的第i种预测方法的误差;
为第i种预测方法在组合预测模型中的权重;p可取不同值,本文p取2;N为模态分量个数;n为预测方法种类数。
基于lp范数的误差平方绝对值之和能够说明两个序列的接近程度,其数值越小,表明预测值越接近实际值,模型的预测效果越好,反之则说明两个序列相差较大,预测效果较差。但是在预测过程中难免会出现误差,因此构建最优化组合预测模型为:
(13)
2 实证结果及分析
2.1 预测结果评估指标
本文选取均方误差(MSE)、平均绝对误差(MAE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)对预测结果的有效性进行评估。
(14)
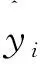
2.2 CEEMDAN_ARIMA_指数平滑预测模型
首先对广东省的碳交易价格序列进行CEEMDAN分解,根据分解序列的均值将其重组为高频序列和低频序列。将2019年1月2日至2021年2月10日的数据作为训练集,对高频序列建立ARIMA模型,对低频序列建立指数平滑模型,然后对2021年2月18日至2021年3月18日的20条数据进行预测,通过将高频序列的预测结果和低频序列的预测结果加和,对广东省碳交易价格进行预测。
2.2.1模型I数据选取
本文选取广东省碳交易每日的收盘价格作为模型I预测研究的基础数据。利用Python 从碳交易网抓取2019年1月2日至2021年3月18日之间广东省碳交易的相关数据,剔除法定节假日等因素的影响,共包含536条数据。
2.2.2CEEMDAN分解与重组
由于碳交易价格具有不平稳、非线性特征,因此对2019年1月2日至2021年3月18日之间广东省碳交易价格进行CEEMDAN分解,由图1可知,CEEMDAN将原始的碳交易价格数据按照频率的高低分为7组不同频率的IMF序列及一组残余趋势序列Res。其本征模函数(IMF)和残余项如图1所示。

图1 CEEMDAN分解产生的IMF及ResFig.1 IMF and Res generated by CEEMDAN decomposition
通过计算本征模函数IMF的均值,将广东省的碳交易价格分解序列重构成高频分量和低频分量,残余项的数值忽略不计。由表1可知,IMF1~IMF6的均值与0相近,而IMF7的分量显著偏离0,因此,本文将IMF1~IMF6加和重构为高频分量,将IMF7重构为低频分量。

表1 各个IMF分量的均值Tab.1 Mean value of each IMF component
2.2.3高频序列ARIMA预测
对高频序列建立差分整合移动平均自回归(ARIMA)模型,为验证该模型的可靠性,选取支持向量机(SVM)模型和长短时记忆网络(LSTM)模型作为基准对照模型。由于ARIMA模型要求序列是平稳序列,因此要对高频序列进行平稳性检验。通过SPSS对训练集的高频序列进行自相关(ACF)和偏自相关(PACF)检验,结果如图2所示。
由图2可知,高频序列的ACF不趋于0,说明序列具有很强的长期相关性,因此该序列为非平稳序列。对高频序列进行一阶差分,使其平稳化,并对一阶差分序列进行平稳性检验,由图3可知,高频序列一阶差分的ACF和PACF均为拖尾,因此其为平稳序列。

图2 高频序列的ACF和PACF图Fig.2 ACF and PACF diagram of high frequency sequence
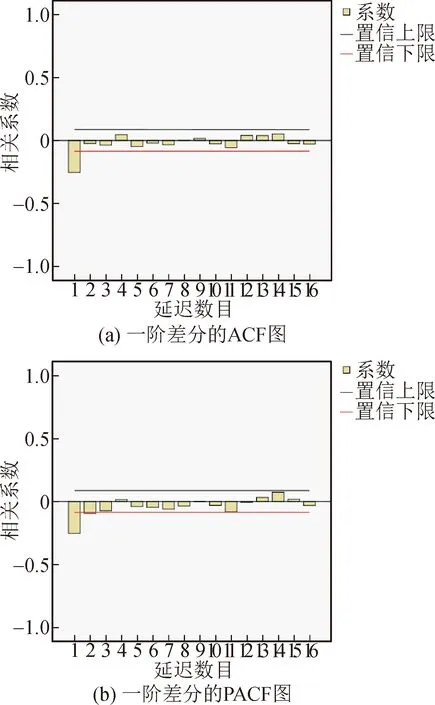
图3 一阶差分的ACF和PACF图Fig.3 ACF and PACF diagram of first-order difference
由图3可知,一阶差分的ACF是一个逐渐趋于0的拖尾,ACF自1阶过后都落在置信区间内,所以是MA(1)模型;一阶差分的PACF是一个逐渐趋于0的拖尾,PACF自3阶过后基本都落在置信区间内,所以是AR(3)模型,因此应对高频序列建立ARIMA(3,1,1)模型。
ARIMA(3,1,1)模型、支持向量机模型(SVM)和长短时记忆网络模型(LSTM)对高频序列的预测精度如表2所示。
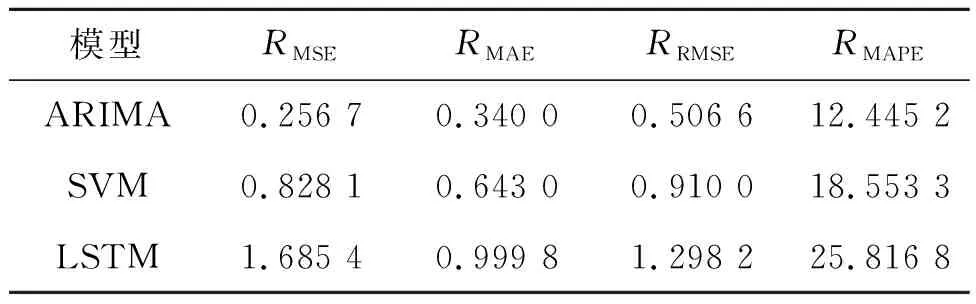
表2 高频序列预测精度对比Tab.2 Comparison of prediction accuracy of high frequency series
由表2可知,ARIMA(3,1,1)模型比支持向量机(SVM)模型的MSE、MAE、RMSE、MAPE值分别降低了69.00%、47.12%、44.33%、32.92%,且ARIMA(3,1,1)模型的预测精度远高于LSTM模型,说明ARIMA(3,1,1)模型对高频序列的预测效果优于其对照模型。
2.2.4低频序列指数平滑预测
由于低频序列具有线性、平稳特征,因此对低频序列采用指数平滑预测。通过对低频数据训练集进行不同平滑次数、不同平滑系数的研究及对比分析,可知当平滑次数为3次、平滑系数为0.1时,模型的预测效果最佳。为验证指数平滑模型对低频序列预测效果的可靠性,选取支持向量机(SVM)模型和长短时记忆网络(LSTM)模型作为基准对照模型,结果如表3所示。

表3 低频序列预测精度对比 Tab.3 Comparison of prediction accuracy of low frequency series
由表3可知,当平滑次数为3次、平滑系数为0.1时,3次指数平滑模型的MSE、MAE、RMSE、MAPE值分别为1.54E-05、0.003 3、0.003 9、0.011 0,均远低于SVM和LSTM模型,说明3次指数平滑模型对低频序列的预测效果优于SVM和LSTM模型。
2.2.5模型I预测结果
相比于SVM模型和LSTM模型,对高频序列建立ARIMA模型、对低频序列建立指数平滑模型预测效果最优。将ARIMA高频序列预测结果和指数平滑模型低频序列预测结果加和,作为2021年2月18日至2021年3月18日的碳交易价格的预测值,并由此得出模型I的预测精度,结果如表4所示。

表4 模型I预测精度Tab.4 Prediction accuracy of Model I
通过对碳交易价格时间序列进行CEEMDAN分解、重组,然后对高频序列建立ARIMA模型,对低频序列建立指数平滑模型,得到模型I预测结果的MSE、 MAE、RMSE、MAPE值分别为0.255 7、0.340 0、0.505 7、1.008 2。
2.3 THHO_ELM预测模型
另一方面,综合考虑碳交易价格的行情指标和经济指标两个维度,从中找出与碳交易价格相关的15个影响因素,通过Pearson相关系数选取与下一日碳交易价格高度相关的6个变量并将其作为解释变量,然后将下一日碳交易价格作为被解释变量,建立多策略融合改进的哈里斯鹰优化极限学习机模型(THHO_ELM),从而对广东省碳交易价格进行预测。
2.3.1模型II数据选取
利用Python 从碳交易网抓取广东省碳交易的相关数据,选取广东省碳交易的最高价、最低价、开盘价、收盘价和交易额5个变量作为行情指标,通过多日内碳交易的行情指标数据计算出碳交易的10个经济指标数据,其中包括12日短期移动平均线(MA12)、26日长期移动平均线(MA26)、平滑异同移动平均线(MACD)、简易波动指标(EMV)、随机指标(K、D、J)、相对强弱指标(RSI)、乖离率和心理线(PSY)。根据当日碳交易的行情指标、经济指标与下一日收盘价的Pearson系数来判定二者之间的相关性强弱,结果如表5所示。
由表5可知,碳交易的最高价、最低价、开盘价、收盘价、MA12和MA26与下一日收盘价高度相关,其相关系数分别为0.971、0.962、0.984、0.989、0.982、0.974。因此,论文将2019年1月2日至2021年2月10日的数据作为训练集,将广东省碳交易的最高价、最低价、开盘价、收盘价、MA12和MA26作为解释变量,下一日碳交易收盘价作为被解释变量,建立哈里斯鹰优化极限学习机模型(THHO_ELM)对2021年2月18日至2021年3月18日的碳交易收盘价进行预测。
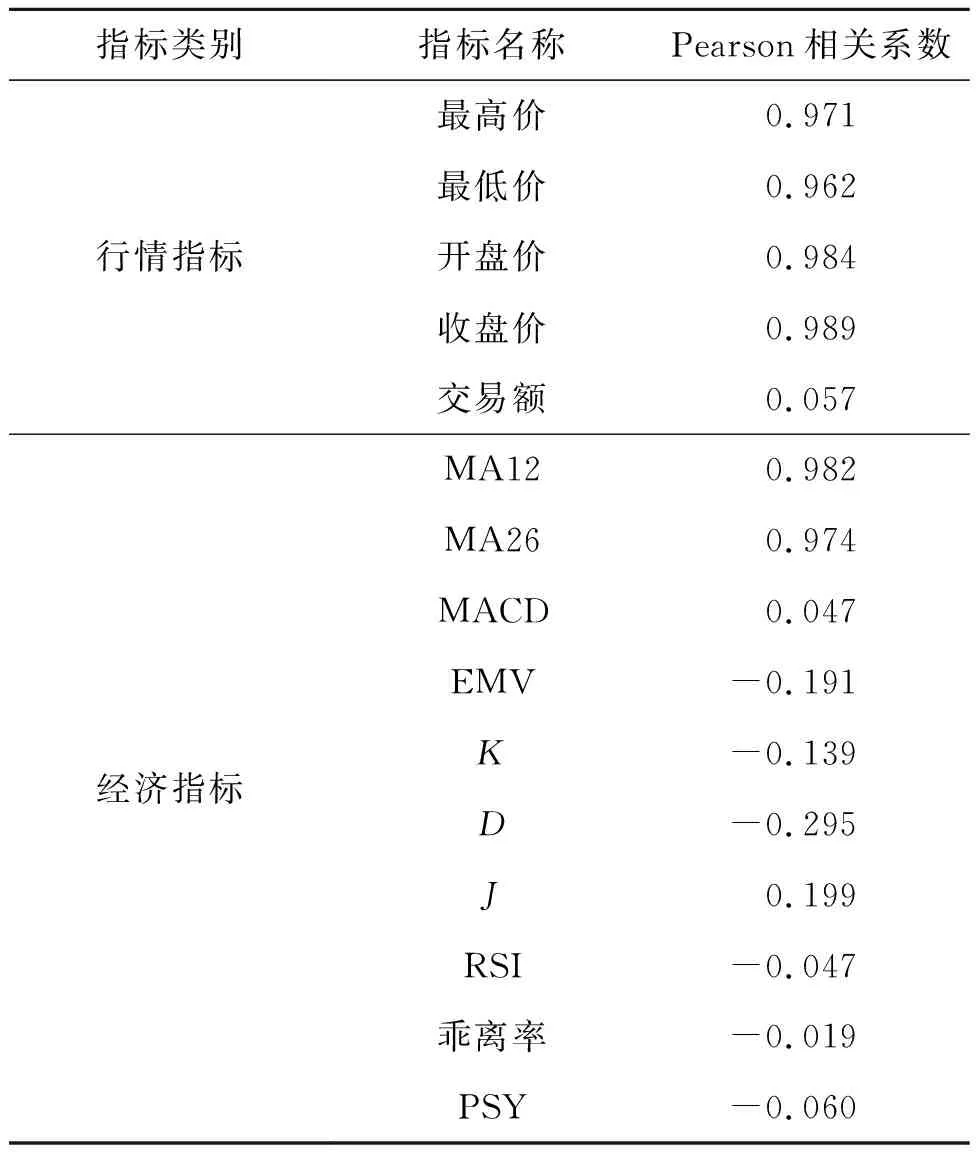
表5 碳交易价格的Pearson相关系数Tab.5 Pearson correlation coefficient of carbon trading price
2.3.2THHO_ELM算法流程
为了提高传统ELM算法的预测准确度,论文利用改进的哈里斯鹰算法对ELM算法的权值和阈值进行优化。其中种群初始规模为50,最大迭代次数为500,ELM算法的权值取值范围为[-1,1],ELM算法的阈值取值范围为[-10,10],THHO_ELM算法具体流程如下:
1) 确定ELM模型的结构,其中主要包括输入层神经元个数、隐含层神经元个数、输入权值数、隐含层节点阈值数;
2) 根据ELM模型进行哈里斯鹰种群初始化,设置种群规模、最大迭代次数等参数,在给定范围内随机产生哈里斯鹰种群;
3) 采用训练集、初始权值和阈值训练ELM模型并对测试集进行预测,将测试集的MSE值作为个体的适应度值,计算哈里斯鹰种群的初始适应度值;
4) 根据逃逸能量E和随机数r的值选择相应的阶段或围攻策略,根据位置更新公式对哈里斯鹰种群进行更新;
5) 计算每个个体的适应度值,更新全局最优值;
6) 判断是否达到算法终止条件,若达到条件,则输出全局的最优适应度值,否则循环执行步骤4)和5);
7) 将哈里斯鹰算法得到的最优位置参数赋值给ELM模型的输入权值和隐层节点的阈值。在训练集样本下,计算ELM的输出权值矩阵,并对测试集样本进行预测。
2.3.3模型II预测结果
将每日的碳交易最高价、最低价、开盘价、收盘价、MA12和MA26作为解释变量,下一日收盘价作为被解释变量,建立ELM模型对碳交易价格进行预测。为了验证ELM模型预测效果的可靠性,选取随机森林模型(RF)、支持向量回归机模型(SVR) 进行对比试验,结果如表6所示。
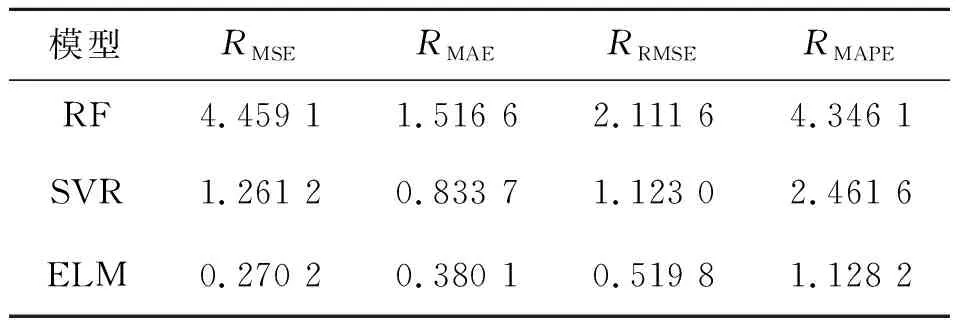
表6 ELM模型预测精度Tab.6 ELM model prediction accuracy
由表6可知,ELM 模型的预测效果要优于RF模型和SVR模型,因此本文选择利用群智能优化算法对ELM模型做进一步优化。
本文选用粒子群算法(PSO) 、灰狼优化算法(GWO)和HHO算法优化ELM模型,对碳交易价格进行预测。结果如表7所示。

表7 ELM优化模型预测精度Tab.7 ELM optimization model prediction accuracy
由表7可知,PSO算法、GWO算法和HHO算法都对ELM模型具有一定的优化效果,且HHO算法的MSE、MAE、RMSE、MAPE值均低于PSO算法和GWO算法,即HHO算法对ELM模型的优化效果优于PSO算法和GWO算法。因此选用HHO算法对ELM模型做进一步优化。
THHO_ELM模型的MSE、MAE、RMSE、MAPE值分别为0.095 3、0.263 1、0.308 6、0.774 2。由ELM模型、HHO_ELM模型和THHO_ELM 模型的MSE、MAE、RMSE、MAPE值可知,HHO算法和THHO算法都能提升ELM模型的预测精度,且THHO_ELM模型的预测精度优于HHO_ELM模型。
为了综合模型优势,将 CEEMDAN-ARIMA-指数平滑模型和 THHO_ELM 模型进行组合,建立基于lp范数的误差平方绝对值模型。
2.4 基于lp范数的组合预测模型
在CEEMDAN-ARIMA-指数平滑模型和THHO_ELM模型的基础上进行lp范数组合预测。当CEEMDAN-ARIMA-指数平滑模型的权值为0.211、THHO_ELM模型的权值为0.789时,模型的组合预测误差最小。基于lp范数的组合预测模型及单一模型的预测结果如表8所示,对比图如图4所示。

表8 lp范数组合预测模型及单一模型的预测结果Tab.8 Prediction results of single model and combined forecasting model based on lp norm

图4 各模型预测对比图Fig.4 Comparison of prediction of each model
由表8可知,基于lp范数的组合预测模型相比于最优的单一预测模型(THHO_ELM),其MSE、MAE、RMSE、MAPE值分别降低了4.72%、9.43%、2.33%、9.74%,说明基于lp范数的组合预测模型优于CEEMDAN-ARIMA-指数平滑模型和THHO_ELM模型。为进一步验证基于lp范数的组合预测模型的预测效果,本文选取文献[21]作为对照,结果表明,基于lp范数的组合预测模型优于对照模型。
此外,考虑到不同碳交易试点的差异性,论文又在我国的东、中、西部分别选取上海、湖北和重庆碳交易试点,并利用上述模型进行预测,结果如表9所示。

表9 碳交易试点模型对比Tab.9 Comparison of carbon trading pilot models
由表9可以看出,基于lp范数的组合预测模型优于其单一预测模型。因此认为,该组合模型对碳交易价格有较好的预测效果。
3 结 语
论文在传统的碳交易价格预测模型的基础上综合考虑了碳交易价格本身和碳交易价格的相关影响因素,分别建立了CEEMDAN-ARIMA-指数平滑模型和改进的哈里斯鹰优化极限学习机的碳价格预测模型。为综合二者优势,论文建立了基于lp范数的组合预测模型,实证结果表明,基于lp范数的组合预测模型相比于最优的单一预测模型,其MSE、MAE、RMSE、MAPE值分别降低了4.72%、9.43%、2.33%、9.74%,取得了较好的预测效果。该组合预测模型可为预测碳交易价格提供参考和借鉴,同时该模型也可应用于其它行业的预测。

