一种基于UWB的CTK-IDS联合定位算法

王文庆,朱 梁,吴益凡

(西安邮电大学 自动化学院,陕西 西安 710121)

目前,全球卫星定位系统(Global Position System,GPS)和北斗导航卫星系统具有应用范围广、定位精度高等特点,在户外可以提供高精度的定位服务[1]。但是,室内环境复杂,卫星信号容易受到障碍物、建筑物的影响,导致卫星定位无法在室内实现精准定位。随着相关室内活动的日益丰富,人们对于室内定位服务的需求也在日益增加[2]。超宽带(Ultra Wide Band,UWB)定位技术作为一种近年来新型的技术,因其精度高、功耗低、时间分辨率高及抗噪声能力强等优点受到广泛关注[3]。

UWB常见的定位模式[4-9]主要包括基于信号到达时间差(Time Difference of Arrival,TDOA)、基于信号到达角度(Angle of Arrival,AOA)、基于信号到达时间(Time of Arrival,TOA)及基于到达信号强度(Received Signal Strength Indication,RSSI)。TDOA通过测量UWB信号从UWB标签到基站之间传播时间的差值[4],得到UWB标签到基站之间的距离差,不要求基站与标签遵循严格的时间同步。AOA定位一般是基于相位差的方式计算出角度,对硬件设备要求较高[5]。TOA基于空中传播时间求出基站与标签的距离,要求发送设备和接收设备时钟始终同步[6]。RSSI是将接收信号强度与传播距离的路径损耗进行定位,环境的变化对定位精度影响极大[7]。为了准确获得UWB标签坐标值,需要准确获取基站和标签之间的距离值,飞行时间测距(Time-of-Flight,TOF)属于点对点的双向测距技术,其主要利用信号在两个异步收发机之间的传输时间测量节点间的距离,测距结果相较于其他测距定位算法更加精准[8]。因此,选用TOF技术测量基站与标签之间的距离值。

近年来,UWB定位技术主要应用于工厂仓库、监狱、展厅及施工场地等室内场景,随着UWB技术的发展,其在室内运动方面的应用逐渐引起重视。室内运动定位系统可以对运动员进行实时定位,能够帮助教练更加全面、系统和具体地了解到运动员的训练情况,从而制定科学、准确的训练策略。文献[9]研究了UWB系统用于篮球运动中的精度与运动员速度干扰问题,提出了一种评估位置数据精度与速度干扰间可靠性的方法。文献[10]分析了UWB系统在曲线运动区间的向心力测量精度。Alejandro Bastida Castillo等[11]研究了UWB系统用于足球运动,对比了误差精度与系统覆盖距离的关系。文献[12]比较了UWB系统和GPS系统在足球运动中的定位精度。文献[13]运用UWB定位系统在室内场地进行步行、慢跑、加速跑和折返跑,测量了运动中的距离、速度及加速度的误差和变化。但是,上述研究没有提出一种具体的提高室内运动定位抗干扰性能的算法。

为了能够满足室内运动定位的高精度定位需求,拟提出一种改进的Chan-泰勒-卡尔曼双边双向(Chan-Taylor-Kalman-Improved Double-Sided,CTK-IDS)联合定位算法。用改进的双边双向测距(Improved Double-sided Two-way Ranging,IDS-TWR)算法计算信号传播时间,然后将Chan算法估计的位置坐标作为Taylor算法的初值点进行迭代,从而解算出运动员的位置坐标。最后,结合Kalman滤波进行坐标的二次估计,获得标签坐标值,以期实现提升测距精度,提高室内运动定位的准确度和系统抗干扰能力。

1 TOF测距算法

在UWB定位系统中常用的TOF测距方式有单边双向(Single-sided Two-way Ranging,SS-TWR)测距和双边双向(Double-sided Two-way Ranging,DS-TWR)测距两种。

1.1 SS-TWR和DS-TWR测距算法

SS-TWR是一种通过一次数据往返就能够测出两个节点间距离的方法[14]。DS-TWR是在SS-TWR的基础上,再增加一次信息传递,其优点是响应时间不用严格相同,测距精度比SS-TWR更高。但是,DS-TWR计算相对复杂,而且时钟偏移引起的误差始终存在,没有考虑环境因素带来的误差干扰[15]。SS-TWR测距流程与DS-TWR测距相比,只进行了一次信息传递,下面重点围绕DS-TWR测距方法进行叙述。DS-TWR测距原理示意图如图1所示。

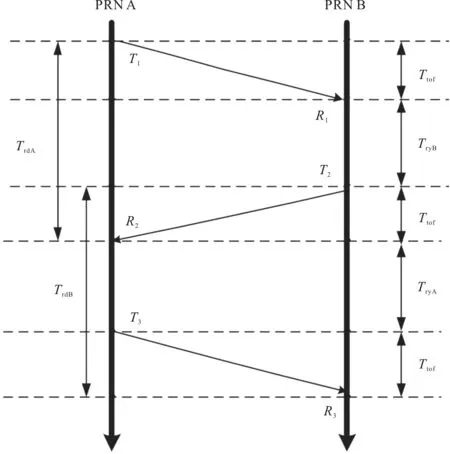
图1 双边双向测距原理

在图1中,DS-TWR测距的具体流程是标签A发送请求数据,记录发送时间T1;基站B收到请求数据,记录接收时间R1;基站延迟一段时间后在T2时刻发送响应数据,该时间为基站延迟时间;标签A收到响应数据,记录接收时间R2,标签A短暂延迟后,在T3时刻发送结束数据,标签A接收基站B的信号,等待一段时间发回至基站B,该段时间称为标签延迟时间;基站B接收结束数据,记录接收时间R3。为便于下文公式的解释,定义标签A发送数据到标签A接收数据的时间差为标签发送数据和接收时间差。定义基站B发送信号至标签A,到标签A发回信号至基站B的时间差为基站发送和接收数据时间差。

基站延迟时间、标签发送数据和接收数据时间差、标签延迟时间及基站发送数据和接收数据时间差的表达式为分别为

Try,B=T2-R1Trd,A=R2-T1Try,A=T3-R2Trd,B=R3-T2

因为信号在收发过程中存在传播时间,标签发送数据和接收数据时间差、基站发送数据和接收数据时间差可以进一步表示为

Trd,A=2Ttof+Try,B

(1)

Trd,B=2Ttof+Try,A

(2)

联立式(1)和式(2)两个方程,信号传播时间Ttof可以表示为

(3)

考虑时钟偏移,假设标签A和基站B的时钟偏移分别是eA和eB,则式(3)可以进一步表示为

(4)

由式(3)和(4)可以得到DS-TWR测距误差为

(5)

由式(5)可知,时钟漂移的大小影响测距精度,为得到更为精确的测距值,需要对测距算法改进。

1.2 改进双边双向测距算法

1.2.1 距离计算修正

通过对考虑时钟偏移后的测距误差分析可知,时钟漂移对测距精度的影响比较大。因此,在DS-TWR的算法上,文献[16]进一步改进时间计算距离的方法。

对式(1)和式(2)进行变换,可得

Trd,A·Trd,B=(2Ttof+Try,B)(2Ttof+Try,A)

(6)

则信号传播时间Ttof可以表示为

(7)

代入时钟漂移eA和eB,式(7)变换为

(8)

由式(7)和式(8)可以得到IDS-TWR测距误差为

(9)

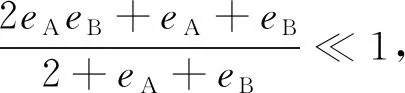
1.2.2 预测拟合修正

空旷的室内环境中信号的接发没有障碍物阻挡,UWB信号的强度与传输时间能够精确的得到[17]。但是,应用到实际室内运动场景中时,信号传播过程中一定会受到观众、教练的阻挡,从而干扰信号传输,增大测距误差。为减小环境因素造成的误差,可以通过线性拟合的方式对测量距离进行预处理,通过测量值寻求距离真实值的最优估计值。

假设在一个UWB定位系统中,基站与标签的位置不变,用DS-TWR的方法多次测量基站与标签之间距离,得出距离平均值为L。多次改变基站与标签的距离,用传统的DS-TWR多次测量距离,求得的平均值分别为L1,L2,L3,…,Ln。对测量平均值需要用数学统计分析里面的线性拟合进行处理,利用线性拟合结果对测量数据进行数据标定。

为了对比算法的精度,需要用标准差和均方根误差判断误差精度的优劣,标准差和均方根误差值越小,算法的性能就越好。标准差和均方根误差的表达式分别为

(10)

(11)

式中:Xi为测量值;X为测量期望值;N为测量次数;dN为参考值与测量值之间的偏差。

2 基于TDOA的室内定位算法

TDOA是基于信号到达时间差的定位模式。该模式是根据标签到两个基站的距离建立双曲线方程[18],然后根据多基站建立双曲线方程组求解获得目标节点的位置。设移动标签的坐标为(x,y),有N(N≥3)个基站,坐标为(xi,yi),i=1,2,…,N。选择基站1为主基站,可以得到主基站到其他基站的距离差为

di,1=cti,1=di-d1,i=1,2,...,N

(12)

式中:di为基站i到标签的距离;ti,1为移动标签到基站i与1号基站的时间差值,c为信号传播速度,约等于真空中的光速。又由二维空间的欧式距离公式可以进一步得到

(13)

由式(12)和式(13)可得联合方程

(14)

其中,

式中:xi,1为基站i与基站1的横向差值;yi,1为基站i与基站1的纵向差值。

式(14)是未知数为x,y和d1的线性方程,可以通过Chan算法和Taylor算法计算出移动标签的坐标。

2.1 Chan算法

Chan算法可以只使用3个基站定位,也可以通过添加基站提高其定位精度。当基站数在4个及4个以上时,算法进行两次加权最小二乘估计求解出标签估计值。

1)当定位场景中只存在3个基站时。将式(14)组成矩阵形式方程为

(15)

将式(15)代入式(13)能得到关于d1的两个解,能够根据先验知识和坐标范围排除其中一个解,就可以得到d1,再由式(15)得到标签的估计坐标。

2)当定位环境中存在4个及4个以上固定基站时。设Za=(x,y,d1)T,将其中的3个元素x,y,d1作为自变量,由式(14)可得到线性方程组

h-GaZa=0

(16)

其中,

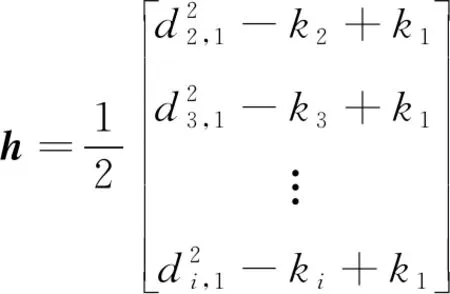
在h,Ga矩阵可逆的情况下,由式(16)基于最小二乘法可获得初始解

(17)

式中,ψ=c2BQB为误差矢量,B=diag(d1,d2,…,dn) 为基站与标签的距离距阵。Q是TDOA测量值误差的协方差矩阵,可近似表示为

(18)

在实际测量中,先用式(18)计算出标签初始位置,估计计算对应B矩阵和ψ的近似值。再用式(17)得到第一次加权最小二乘解的估计结果Za。估计结果与真实值的关系分别为

Za,1=x+e1Za,2=y+e2Za,3=d1+e3

Za是在假设Za中的3个元素相互独立的情况下得到的,但在实际中Za的3个元素相关,而且Q近似代替ψ也会有误差。因此,用Za的元素重新构造一个方程组,再进行第二次加权最小二乘估计可以减小误差,其表达式为

(19)

其中,

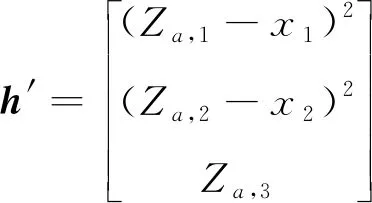
再经过第二次加权最小二乘解估计出最终位置估计坐标信息为

(20)

2.2 Taylor算法

Taylor算法是一种需要初始估计位置的递归算法,优点在于可以应用于各种环境,并能在一定程度上抑制非视距误差(Non-Line of Sight,NLOS)。

假设有一个初始估计位置坐标为(x0,y0),参考坐标为(x,y),Δx,Δy为坐标偏差。在(x0,y0)处进行泰勒展开,忽略二阶及以上的高阶分量,式(14)可以转换为

ψ=h-Gaδ

(21)

其中,

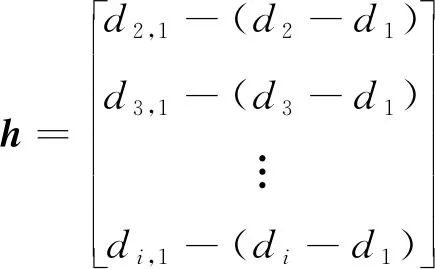
不断使用最小二乘算法迭代计算δ,直至初始值满足|Δx+Δy|<ε,ε为设定的阈值。

2.3 CTK-IDS联合定位算法

为克服Chan算法在NLOS环境下精度低,以及Taylor算法初始值选取困难的问题,引入Kalman滤波技术加以改进。先用IDS-TWR算法获得TDOA值,然后利用Chan算法得到标签的初始估计坐标,进而将该坐标作为Taylor算法迭代的初始点,得到更为精准的标签估计坐标。最后利用Kalman滤波对估计坐标进行二次估计,去除环境因素导致的异常数据,使定位结果更加精确和稳定。

在获得Chan-Taylor算法解算出的标签坐标之后,运用卡尔曼滤波对坐标进行二次估计,使得定位结果更加精确和稳定。卡尔曼滤波算法是使用上一次的最优估计结果预测当前状态的值,同时用当前状态的观测值修正,从而得到当前状态的最优估计结果。

卡尔曼滤波的状态方程和观测方程的表达式分别为

xt=Fxt-1+But+WtZt=Hxt+vt

式中:xt为t时刻的状态;ut为系统的控制量;Wt为过程噪声;zt为观测量;vt是观测噪声;F为状态转移矩阵;B为输入控制矩阵;H为观测矩阵。

运用卡尔曼滤波进行二次估计第一步是状态预测,根据前一时刻的状态和系统输入量预测当前时刻的状态,并计算出估计值的协方差矩阵。第二步是进行更新,引入卡尔曼增益,将当前时刻的测量值与估计值反馈给当前状态的估计值,根据更新后的协方差矩阵和卡尔曼增益计算当前时刻的最优估计。

将Chan-Taylor融合算法估计的标签坐标信息作为卡尔曼滤波的输入值,进行标签位置坐标的二次估计,最后得到标签位置的最优估计值。

2.4 不同算法的仿真对比

为了更直观地体现出CTK-IDS联合定位算法的性能,通过仿真软件将Fang算法,Chan算法,Taylor算法,Chan-Taylor算法与CTK-IDS算法进行对比。

实验环境配置的仿真场地参照标准篮球场半场,大小为15 m×15 m,4个基站的位置信息分别为BS1(0,0),BS2(15,0),BS3(15,15),BS4(0,15)。

设定标签参考坐标为(1300,1400)(单位:cm),不同算法运行各得到2 000组估计点。为了更直观地对比出散点分布的差异,将不同算法的散点分布放在一起比较,结果如图2所示,相较于其他算法,CTK-IDS估计位置的离散度最小,即定位精度最高。

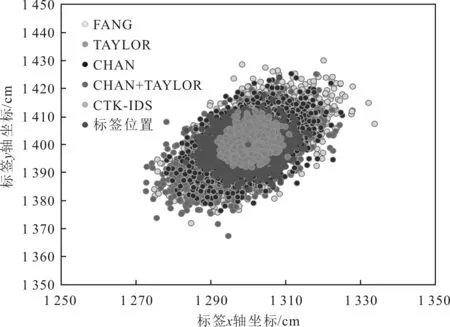
图2 不同算法散点分布比较

累计分布函数(Cumulative Distribution Function,CDF)是对概率密度函数进行积分得到,可以用于描述定位精度的好坏,X轴为定位误差,Y轴为误差累计概率,CDF值越大表示定位精度越高。对不同算法的定位结果进行CDF构建,比对情况如图3所示。CTK-IDS算法定位的结果90%以上都在8 cm范围内。表1为不同算法进行5×2 000次位置估计的平均误差和均方根误差,CTK-IDS算法的平均误差和均方根误差最小。因此,CTK-IDS算法相比于Fang算法、Chan算法、Taylor算法和Chan-Taylor算法精度有所提高。

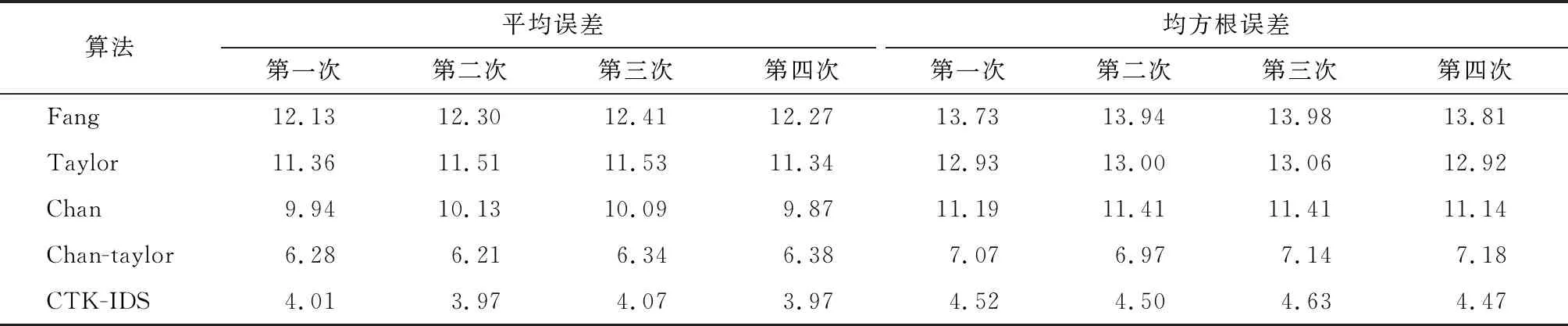
表1 不同算法进行4×2 000次位置估计的平均误差、均方根误差/cm

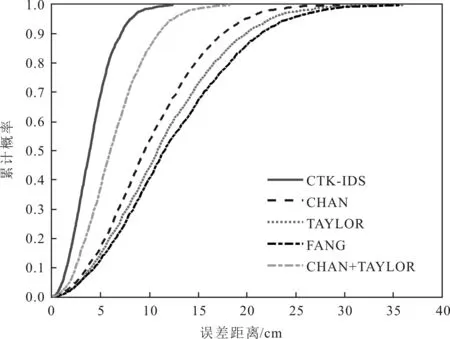
图3 不同算法的CDF对比结果

3 验证结果及分析

为了进一步验证CTK-IDS联合定位算法的性能,将分别进行测距实验和室内轨迹定位实验,实验需要4个基站和1个标签。

3.1 测距实验

在室内篮球场搭建实验环境,将基站和移动标签分别放置在同一高度,分别用DS-TWR和IDS-TWR测距方法进行测距实验,基站A与标签进行测距实验,由3 m到21 m,每隔3 m测一次距离,每次测6 000组数据,采样频率为1 s测100组数据。

为了可以直观表现出IDS-TWR的测距精度优于DS-TWR,分别进行了7组测距实验,具体的测距结果分别如表2、表3和表4所示。

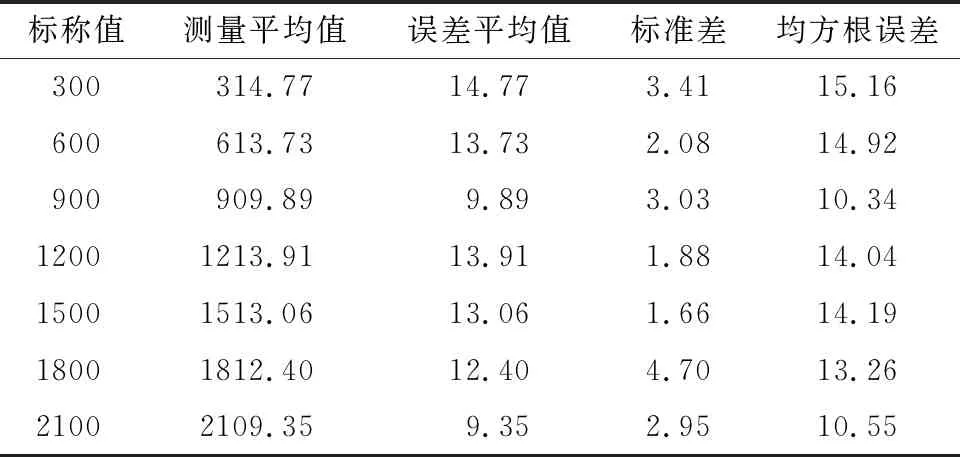
表2 DS-TWR测距结果 单位：cm

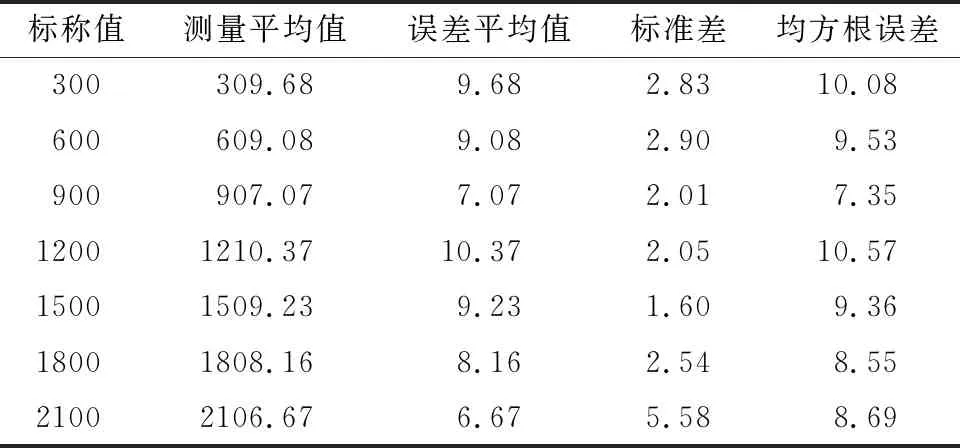
表3 未进行线性拟合的测距结果 单位：cm

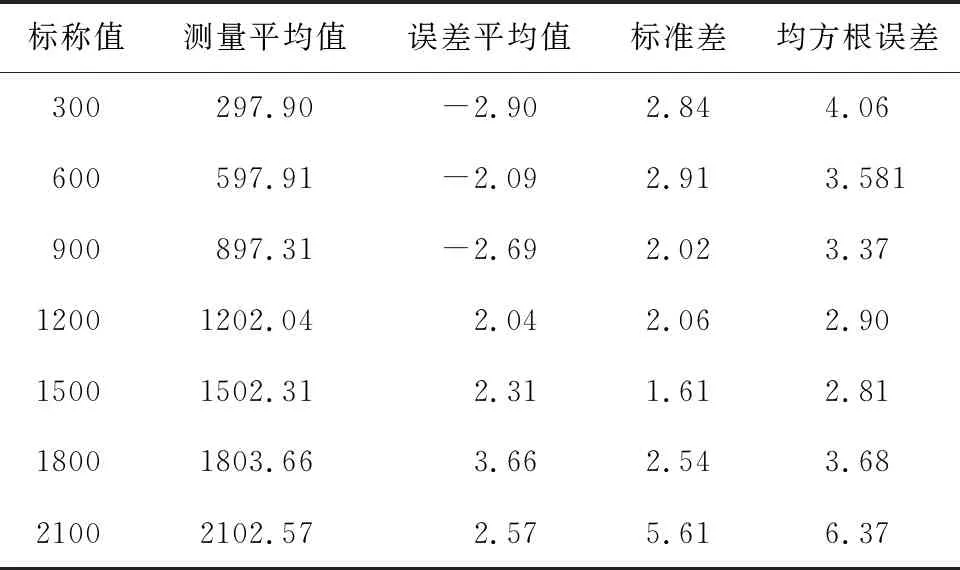
表4 IDS-TWR测距结果 单位：cm

表2是DS-TWR测距方法进行实验的数据结果,表3是未进行线性拟合的数据结果。由表2和表3可以看出,算法进行距离修正之后,DS-TWR算法测距精度提升了,但在测距实验中存在一些环境因素降低了测距精度,导致测距误差还是很大。因此,需要对测距值进行拟合修正,降低测距误差。对测距值取平均,并对其线性拟合,线性拟合结果如图4所示。

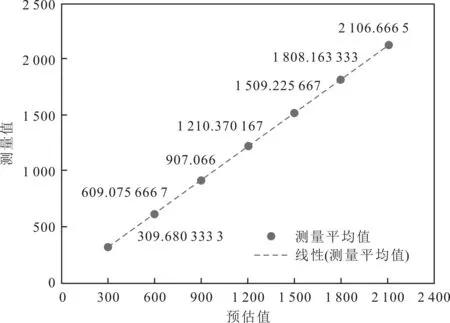
图4 线性拟合结果

由表2和表4可以得到IDS-TWR相比较于DS-TWR,测距平均误差降低,均方根偏差明显减少。由表3和表4可以得到,数据标定后的测距结果平均误差减少了,均方根误差明显降低。为了直观对比出DS-TWR算法和IDS-TWR算法测距误差,分别在测距误差为3 m和18 m的情况下进行对比,具体的测距误差分布对比情况如图5所示。由图5可以看出,在3 m测距误差分布中,DS-TWR误差分布在7～27 cm,IDS-TWR误差分布在8 cm以内;在18 m测距误差分布中,DS-TWR误差分布在5～18 cm,IDS-TWR误差分布在7 cm以内。因此,IDS-TWR测距误差要比DS-TWR测距误差偏差更小。

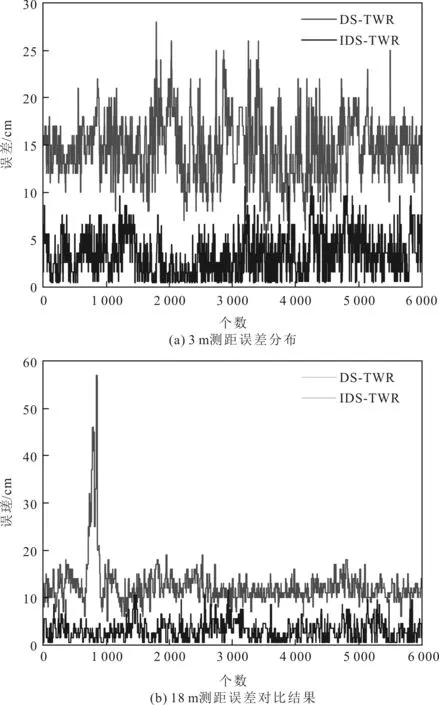
图5 DS-TWR与IDS-TWR算法测距误差对比结果

从实验结果可以看出,DS-TWR测距误差明显大于IDS-TWR测距误差,且误差分散较大。但是,IDS-TWR算法测距误差在3 cm以内,测距结果相对稳定,与DS-TWR算法相比误差波动较小。

3.2 轨迹定位实验

预设轨迹定位测试可以分成两个移动轨迹测试,采用CTK-IDS算法对运动员进行定位。首先,以(350,350)为起点,经(800,350)、(800,850)、(350,850)作一个长为450 cm,宽为500 cm的矩形。其次,以(800,500)为圆心作半径为300 cm的圆。图6中线条为预设轨迹,运动员携带移动标签按照预设路径进行跑动,采集运动员位置信息,解算标签位置,通过上位机实时显示运动员移动轨迹,可以直观看到室内运动定位系统的定位性能。运动员运动轨迹如图6所示。在图6中,可以看出运动员移动轨迹平滑,轨迹偏离的地方误差最大也不超过13 cm,误差波动小,能够满足室内运动定位的要求。

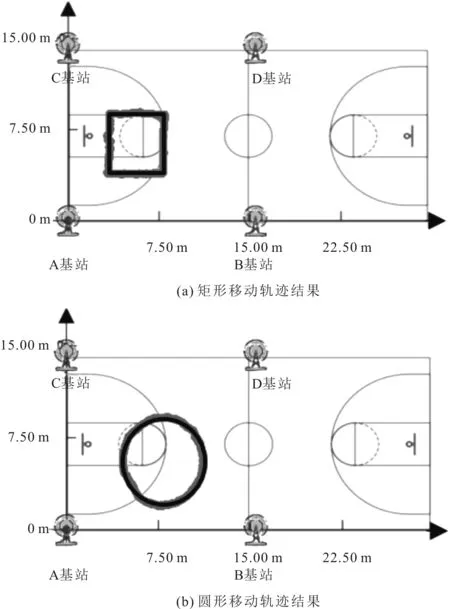
图6 预设轨迹定位结果

4 结语

利用UWB实现运动员在室内环境中的实时精准定位,在IDS-TWR测距算法、Chan算法、Taylor算法与Kalman滤波的基础上提出了CTK-IDS联合定位算法。通过测距计算修正与预测拟合技术,采用IDS-TWR算法计算信号传播时间。同时,将Chan算法估计的位置坐标作为Taylor算法的初值点进行迭代,结合Kalman滤波进行坐标的二次估计,从而实现运动员室内运动环境中的实时、精准定位。比对实验结果表明:CTK-IDS算法在定位精度和抗干扰能力比其他算法要更好;IDS-TWR测距算法能够将测距平均误差控制在4 cm以内,测距误差波动小;CTK-IDS联合定位算法定位的最大定位误差不超过13 cm,定位误差波动小、数据较为稳定,定位精度高,能够满足室内运动定位的要求。